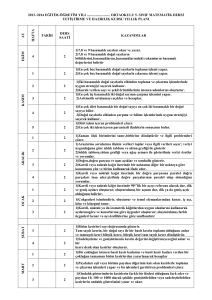
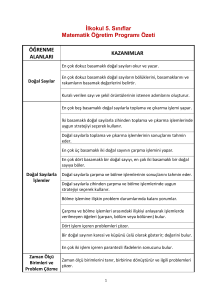
SAYMA PROBLEMLERİ
1. 15 farklı elma ve 10 farklı şeftali verilmiştir. Önce Ali bir elma veya
şeftali alıyor, sonra Betül bir elma ve bir şeftali alıyor. Bu işlem, kaç
yolla olabilir?
2. Bir beyaz ve bir kırmızı zar birlikte 2 kez art arda atıldığında kaç
sonuçta birinci atıştaki zarların toplam değeri ikincisinden büyüktür?
3. 1 ’den 10000’e kadar olan tüm pozitif tam sayıları yazdığımızda 5
rakamını kaç kere kullanmış oluruz?
4. 3, 3, 4, 4, 5, 5, 5, 6, 6 sayılarından en az ikisinin çarpımı kaç farklı değer
alabilir?
5. {1, 2, 3, . . . , 10} kümesinden kaç yolla boş olmayan ve birbiriyle kesişmeyen iki alt küme alınabilir?
6. Bir dörtyüzlünün yüzleri, aynı renkten olan iki yüz bulunmayacak şekilde, 4 değişik renkle kaç yolla boyanabilir (dörtyüzlünün dönmesiyle
birbirinden elde edilen iki boyama şekli aynı kabul ediliyor)?
7. A = {1, 2, 3, 4} kümesinin her a elemanı için f (f (f (f (a)))) = a koşulunu sağlayan kaç tane f : A → A fonksiyonu vardır?
8. Düzlem üzerinde birbirinden farklı n tane doğru verilmiştir. Bunlardan
her biri diğerlerinin tam 2004 tanesiyle kesişiyor. n kaç farklı değer
alabilir?
9. n elemanlı bir kümenin tek sayı elemanlı alt küme sayısı kaçtır?
10. Beş kişi birkaç tane ikili tenis maçı yapıyor. Her kişi herhangi bir
diğeriyle tam bir kere aynı takımda ve tam iki kere rakip takımlarda
yer alıyor. Toplam maç sayısını bulunuz.
11. Satranç tahtası üzerinde 8 kale birbirini tehdit etmeyecek şekilde ve
tahta saat yönünde 90◦ döndürüldüğünde aynı durum elde edilecek şekilde kaç yolla yerleştirilebilir?
12. Tüm basamakları 0 dan farklı olan ve basamaklarındaki rakamlar nasıl
sıralanırsa sıralansın oluşan sayıların hepsinin 7 ile bölündüğü kaç tane
altı basamaklı pozitif tam sayı vardır?
1
13. {1, 2, . . . , 9} kümesinin kaç tane altkümesi iki ardışık sayı içermiyor?
14. 50 yapraklı bir kitabın sayfaları 1, 2, . . . , 99, 100 sayıları ile numaralandırılmıştır. Bu kitaptan birkaç yaprak koparılıp atıldıktan sonra, geriye
kalan sayfaların numaralar toplamı 4946 olmuştur. Bu durumda en fazla
kaç yaprak koparılmıştır?
15. 6 farklı kişiye 6 mektup yazıldı ve üzerine bu kişilerin adresleri yazılı 6
zarf hazırlandı. Hiç bir kişinin adı yazılan zarfa bu kişiye yazılan mektup
konulmayacak şekilde kaç yolla her zarfa birer mektup konulabilir?
16. 1 den 16 ya kadar olan tüm tam sayıları
(a) bir doğru boyunca;
(b) bir çember boyunca
her iki komşu sayının toplamı bir tam kare olacak şekilde dizmek mümkün müdür?
17. Doğru üzerinde bir kaç nokta alındı Sonra her iki komşu nokta arasında
bir nokta daha alındı. Bu işlem iki kez daha yapıldı (toplam üç kez).
Sonuçta doğru üzerinde 113 nokta olduğuna göre başlangıçta kaç nokta
alınmıştır?
18. 0, 1, 8 sayıları yazılmış olan kağıdı çevirirsek aynı sayıları elde ederiz;
6 veya 9 sayısı yazılmış olan kağıdı çevirirsek 6 sayısı 9 olur ve tersine
9, 6 olur. Diğer sayıları çevirdiğimizde anlamlı bir sayı elde etmiyoruz.
Kağıt çevrildiğinde değişmeyen kaç tane dokuz basamaklı sayı bulunur?
19. 1, 2, . . . , 9 sayıları çember üzerinde, herhangi iki komşu sayı alındığında
bunların toplamı 3, 5 ve 7 sayılarının hiçbirine bölünmeyecek şekilde
yerleştirilebilir mi?
20. Tavla zarının iki karşı yüzüne birer, diğer iki karşı yüzüne ikişer ve
geriye kalan iki karşı yüzüne de üçer nokta konulmuştur. Böyle zarlardan 8 tanesi alınarak 2 × 2 × 2 boyutlu bir küp oluşturulmuştur. Küpün
yüzlerindeki nokta sayıları 6 ardışık tam sayı olabilir mi?
2
21. a doğal sayısı dört ayrı asal sayının çarpımının karesi olsun. k ve n, a’nın
k|n koşulunu sağlayan pozitif bölenleri olmak üzere, (k, n) ikilileri kaç
tanedir?
22. 6050 ’nin böleni olup, 5060 ’ın böleni olmayan pozitif tam sayıların sayısı
n olsun. n sayısının 50’ye bölümünden elde edilen kalan kaçtır?
23. Verilen altı değişik rengi kullanarak bir küpün her yüzünü farklı bir
renge boyuyoruz. Küpün istenildiği kadar ve istenen istikametlerde döndürülmesiyle biri diğerinden elde edilen iki boyamayı aynı kabul edersek, bu
boyama işlemi kaç değişik biçimde yapılabilir?
24. İçlerinde a, b ve c’nin de bulunduğu 10 değişik harfin permütasyonlarından kaç tanesinde a, b ve c harflerinden ikisi yan yana gelmez?
25. 13 kişilik bir topluluk, her birinde en az bir kişi bulunan iki alt topluluğa kaç farklı şekilde ayrılabilir?
26. Rakamlarının sayı değerleri çarpımı 90 olan kaç tane beş basamaklı
pozitif tam sayı vardır?
27. Bir kübün köşesinde bulunan bir örümcek sadece kübün kenarları boyunca hareket edebilmektedir. Her noktadan en fazla bir defa geçmek
koşuluyla, bu örümcek bulunduğu köşeye en uzaktaki köşeye kaç farklı
yoldan gidebilir?
28. Ondalık yazılımında 4 ve 5 rakamlari bulunup, 0 ve 8 rakamları bulunmayan kaç tane 10 basamaklı sayı vardır?
29. {1, 2, . . . , 99, 100} kümesinden herhangi ikisinin farkı 7 olmayacak şekilde en çok kaç eleman seçilebilir?
30. a ve b’den oluşan 9 harfli dizilerden kaç tanesi baba kelimesini içerir?
31. Ondalık yazılımlarında hiçbir rakamın yan yana tekrarlanmadığı ve
1 ≤ n ≤ 101997 koşulunu sağlayan kaç n tam sayısı vardır?
32. Bir kübün yüzlerini 1, 2, 3, 4, 5, 6 sayılarını işaretleyerek bir zar yapmak
istiyoruz. Ortak bir ayrıta sahip iki yüze komşu yüzler dersek, ardışık
sayıların komşu yüzler üstünde yer alması koşuluyla, bu zarı kaç değişik
biçimde yapabiliriz?
3
33. Tüm basamaklarındaki rakamlar birbirinden farklı olan ve 11111 ile
bölünen on basamaklı kaç tamsayı vardır?
34. Ondalık yazılımında tüm basamakları tek olan 5 basamaklı tam sayılardan kaç tanesinin en az iki ardışık basamağının toplamı 10’dur?
35. İstanbulspor, Yeşildirek, Vefa, Karagümrük ve Adalet takımlarından
her biri, geri kalan dördüyle tam olarak birer maç yapıyor. İstanbulspor,
Yeşildirek hariç tüm takımları yeniyor; Yeşildirek, İstanbulspor’u yenip,
diğer bütün takımlara yeniliyor. Vefa, İstanbulspor dışındaki bütün
takımları yenerken, Karagümrük-Adalet maçını Karagümrük kazanıyor.
Bu beş takımı, sonuncusu hariç her takım, kendinden bir sonra gelen
takımı yenmiş olacak biçimde kaç değişik şekilde sıralayabiliriz?
36. 10×10 bir satranç tahtasında, her k ∈ {1, 2, . . . , 10} için, k. satırda soldan k−1 ardışık kareyi atarak elde edilen merdiven biçimindeki şekilde,
birim karelerin bileşiminden oluşan kaç farklı dikdörtgen vardır?
37. İçlerinde siyah ve beyaz toplar olan iki torbada toplam 25 top var.
Her torbadan rasgele birer top alındığında her ikisinin de beyaz olma
olasılığı 0,54 ise, her ikisinin de siyah olma olasılığı nedir?
38. Yalnızca 1, 6 ve 9 rakamları kullanılarak yazılan pozitif tam sayıları
1, 6, 9, 11, 16, . . . diye küçükten büyüğe doğru dizelim.
(a) 1996’nın bu dizinin kaçıncı terimi olduğunu bulunuz.
(b) Bu dizinin 1996’ıncı terimini bulunuz.
39. 3 × 3 bir satranç tahtasına 1’den 9’a kadar olan tam sayılar, her kareye
bir sayı gelecek biçimde yerleştiriliyor. Her sütun için o sütunda yer
alan sayıların en küçüğünü alarak bulduğumuz üç sayının en büyüğüne
a diyelim. Her satır için ise, o satırda yer alan sayıların en büyüğünü
alarak elde ettiğimiz üç sayının en küçüğüne b diyelim. Sayıları tahtaya
a = b = 4 olacak şekilde en fazla kaç biçimde yerleştirebiliriz?
40. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} kümesinin, herhangi iki ardışık tam sayı
içermeyen kaç alt kümesi vardır?
4