1
KONTROL KARTLARI
1)DEĞİŞKENLER İÇİN KONTROL KARTLARI
Ölçme,gözlem veya deney yolu ile elde edilen veriler değişken(ölçülebilir-sürekli) ve özellik
(sayılabilir-kesikli) olmak üzere başlıca iki gruba ayrılır. Değişken veriler belirli bir birim
sistemi içinde ölçülebilen ve genelde sayılarla ifade edilen verilerdir; örneğin bir parça
çapının ölçülmesi ve mm olarak ifade edilmesi gibi. Diğer taraftan özellik verileri ‘’uygun’’
veya ‘’uygun değil’’ olarak ifade edilen verilerdir; örneğin mastarla kontrol edilen ve
geçer/geçmez,veya kusurlu/kusursuz,veya defolu/defosuz
şeklinde ifade edilen
verilerdir.Kontrol kartları değişkenler ve özellikler için olmak üzere başlıca iki çeşittir.
Kontrol kartları prosesin kontrolü için en uygun kontrol araçları olmakla beraber,amaçları
genelde şu şekilde açıklanabilir.
•Proseste sapmaları ve prosesin kararlı olup olmadığını gösterir.
•Kontrol edilen ürün özelliğinin,üst ve alt kontrol limitleri denilen iki çizgiye göre trendini
gösterir
•Özelliğin değeri kontrol limitlerini aştığı durumda,bunun nedeninin tayin edilmesini ve
düzeltme önlemlerinin alınması gerektiğini gösterir.
•Proses yeterliliğin tayin edilmesine yardımcı olur.
•Kalitenin iyileştirilmesi için en iyi önlemdir.
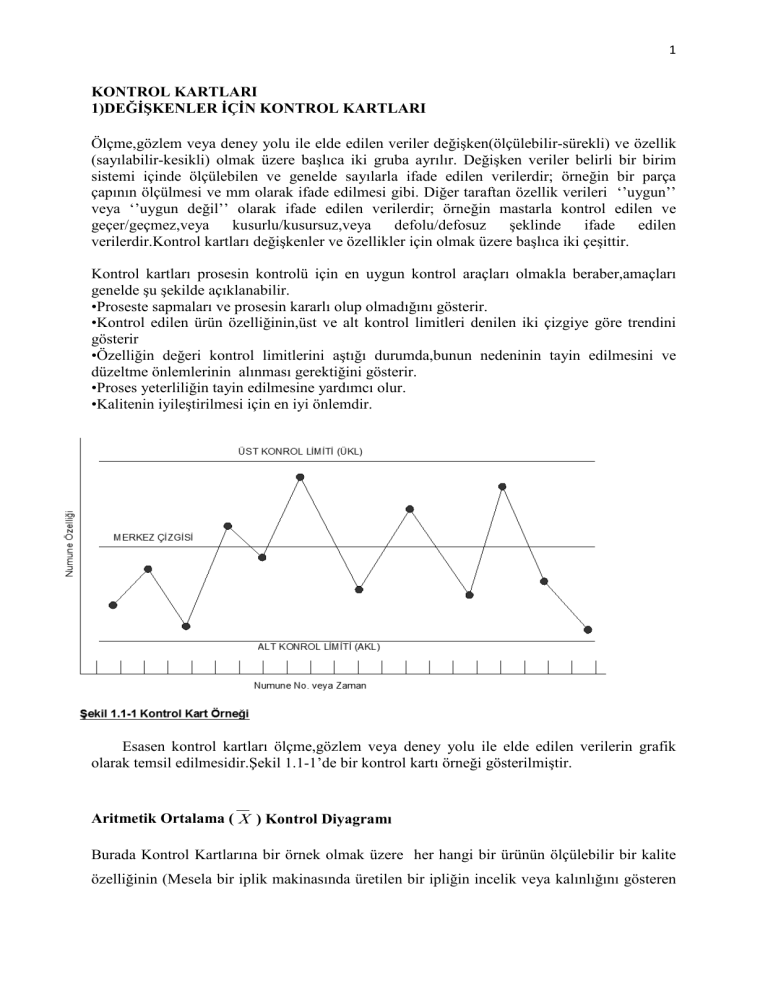
Esasen kontrol kartları ölçme,gözlem veya deney yolu ile elde edilen verilerin grafik
olarak temsil edilmesidir.Şekil 1.1-1’de bir kontrol kartı örneği gösterilmiştir.
Aritmetik Ortalama ( X ) Kontrol Diyagramı
Burada Kontrol Kartlarına bir örnek olmak üzere her hangi bir ürünün ölçülebilir bir kalite
özelliğinin (Mesela bir iplik makinasında üretilen bir ipliğin incelik veya kalınlığını gösteren
2
iplik numarasını veya torna tezgahında imal edilmekte olan silindirik bir parçanın çap
değerinin ortalama değerini gözlemlemekde kullanılan Ortalama ( X ) Kontrol Kartı ile bu çap
değerlerinin dağılımını gözlemlemekde ve kontrol etmekde kullanılan (R) kartının nasıl
oluşturulduğunu göreceğiz.
Aritmetik Ortalama ( X ) Kontrol Diyagramının dizaynı
Ortalamalarla ilgili X kontrol diyagramı sürekli değişkenlik gösteren yani ölçülebilen
örneklerin ortalamalarında meydana gelen değişmeleri izlemede kullanılmaktadır.
X kontrol diyagramı için kontrol sınırlarının hesaplanması ilgilenilen kalite karakteristiğine
ait µ ve σ’nın bilinmesi durumunda
ÜKL = μ + Aσ
MÇ = μ
AKL = µ - Aσ
Şeklinde hesaplanır. Burada ÜKL Üst kontrol limiti, AKL Alt kontrol limiti ve MÇ Merkez
çizgiyi simgelemektedir. A katsayısı ilgili tablolardan n örnek hacmine göre bulunan bir
katsayı olup A = 3/ n dir.
Ancak çoğu kez ortalama değer µ nün ve standart sapma σ nın gerçek değerleri
bilinmeyebilir. Bu durumda sürecin ilgilenilen kalite karakteristiğine yönelik her biri n
birimden oluşan m adet örnek alınır. X ij i. örneğin, j. ölçüm değeri, j = 1, 2, 3,.....n olmak
üzere, i. örneğin ortalaması,
n
Xi =
∑X
j =1
ij
n
olur. Kontrol diyagramının merkez çizgisi de, bir başka ifadeyle süreç ortalaması, örnek
ortalamalarının ortalaması olan ve
m
X=
∑X
i =1
m
i
3
şeklinde tanımlanan genel ortalama ile belirlenir. Genel ortalama (örnek ortalamaların
ortalaması), X , süreç ortalaması µ’nün yansız bir tahminleyicisidir.
Değişkenlik ölçüsü standart sapma σ verilmediğinde bunu tahmin etmek için örneklerden
hesap edilen değişim aralığı R değerinden istifade edilir. Burada;
R = X max - X min bir örneğin değişim aralığı olup m örneğin değişim aralıklarının ortalaması
R=
R1 + R2 + ⋅ ⋅ ⋅ ⋅ ⋅ + Rm
olur. Bu durumda sürecin standart sapması,
m
R
σ =d
olarak tahmin edilir. Böylece σ yerine tahminleyicisi yazıldığında,
2
X kontrol diyagramının parametreleri sonuçta,
ÜKS x = X + A2 R
MÇx = X
AKS x = X − A2 R
şeklinde bulunur.
Eğer sürecin standart sapmasının tahmininde, örnek varyansı S kullanılırsa X
kontrol
diyagramının parametreleri,
ÜKS = X + A3 S
MÇ = X
AKS = X − A3 S
olarak elde edilir.
Değişim Aralığı ( R ) Kontrol Diyagramı
R diyagramı örneklere ait değerlerin değişim aralıklarının değişkenliğini izlemek amacıyla
kullanılmakta olup ilgili kalite karakteristiğinin dağılmanın araştırılmasında en yaygın olarak
başvurulan araçtır. Bu tür kontrol grafiklerinde merkez çizgi, daha önce ifade edildiği gibi R
4
ile yani örneklerin değişim aralıklarının ortalaması ile gösterilmektedir. Yine burada kalite
karakteristiğinin ortalama değeri ve standart sapması σ ile ilgili olarak bilgi verilmemiş ise
kalite karekteristiğin değişkenliğini izlemek ve kontrol etmek üzere değişim aralığı R den
istifade edilir.
Üretimden belirli aralıklarla alınan bir örneği oluşturan n birim X 1 , X 2 , .......X n ise X i ’lerin en
büyüğü ve en küçüğü sırasıyla X max ve X min olmak üzere değişim aralığı,
R = Xmax – Xmin
Eğer her biri n birimden oluşan m tane örnek alındığında, j. örneğin değişim aralığı Rj olmak
üzere değişim aralıkları ortalaması,
m
R=
Rj
∑
j
=1
m
olarak hesaplanır.
R kontrol diyagramının parametreleri D 3 ve D 4 e bağlı olarak
ÜKL = D 4 R
MÇ = R
AKL = D 3 R
Olarak yazılır.
Örnek Problem. Bir meşrubat dolum makinesinin dolum işlemini yeterince hassas yapıp
yapmadığını araştırmak için 1000 ml olarak doldurulan ürünlerden 10 dakika ara ile 5
birimden oluşan örnekler çekilmiş ve aşağıdaki sonuçlar elde edilmiştir. Bu verilerden
hareketle
a) X (aritmetik ortalama)kontrol diyagramını
5
b) R (değişim aralığı) diyagramını çizip prosesin kontrol altında olup olmadığını belirtiniz.
X1
X2
X3
X4
X5
1
1002,3
1001,7
1000,9
997,6
1002,3
5004,8 1000,96
4,7
2
999,2
1001,5
1002,9
998,7
999,6
5001,9 1000,38
3,8
3
1003,2
1001,8
998,9
1002,3
996,8
5003
1000,6
6,4
4
998,3
999,6
996,5
999,1
1000,2
4993,7
998,74
3,7
5
998,1
999,2
1001,2
995,8
997,6
4991,9
998,38
5,4
6
995,7
998,3
999,4
1002,3
996,1
4991,8
998,36
6,6
7
1002,3
1001,6
1004,2
1003,8
999,5
5011,4 1002,28
4,7
8
1003,5
1001,6
1004,7
1001,2
998,2
5009,2 1001,84
6,5
9
997,6
1003,5
1001,2
999,2
1004,5
10
1003,2
1002,1
997,6
1004,2
1002,6
X=
i =1
m
5006
10004,68
=
⇒ X = 1000,468
10
R=
∑R
i =1
m
i
=
6,9
5009,7 1001,94
6,6
55,3
⇒ R = 5,53
10
X diyagramı için kontrol sınırları
MÇ= X = 1000,468
ÜKS = X + A 2 R
Xi
1001,2
10
10
∑ Xi
Toplam
Ri
Örnek no
n = 5 için A 2 = 0,58 ( tablodan )
ÜKS = 1000,468 + 0,58 ( 5,57 ) = 1000,468+3,2074 = 1003,57
AKS = X - A 2 R = 1000,468 - 0,58 ( 5,57 ) = 1000,468+3,2074 = 997,24
6
X ortalama
diyagrami
1004
ÜKS= 1003,57
Örnek ortalamasi
1003
1002
1001
MÇ=1000,47
1000
999
998
AKS = 997,24
997
0
1
2
3
4
5
6
7
8
9
10
Örnek no
Şekil 7.2 Aritmetik Ortalama ( X ) Kontrol Diyagramı
Yukarıdaki aritmetik ortalama diyagramına göre tüm örnek ortalamaları kontrol sınırları içine
düştüğünden merkezi değerin kontrol altında olduğu anlaşılmaktadır.
R diyagramı için kontrol sınırları
MÇ = R = 5,57
ÜKS = D 4 R olup, n = 5 için D 4 = 2,115
ÜKS = 2,115 ( 5,57 ) = 11,78
AKS = D 3 R olup, n = 5 için D 3 = 0
AKS = 0
Değişim Aralığı ( R ) Kontrol Diyagramı
Yukarıdaki değişim aralığı diyagramı incelendiğinde değişkenliğin (R) kontrol altında olduğu
anlaşılmıştır.
7
NİTELİKSEL
2)
(ÖZELLİKLER-SAYILABİLEN)
İÇİN
KONTROL
DİYAGRAMLARI
Ürünlerin taşıması gereken kalite karakteristiklerinin biri ya da bir kaçı belirlenen
spesifikasyonlara uymayabilir. Nitelik olarak adlandırılan bu özellik nedeniyle ürün belirli bir
gruba alınır. Ürünün sağlamadığı her bir spesifikasyon bir uyumsuzluk ya da kusur olarak
tanımlanır. Böyle özellikteki ürün ise, uygun olmayan ya da kusurlu ürün olarak tanımlanır.
Niteliksel kontrol diyagramlarında ya kusurlu parça sayısı ya da bir parça üzerindeki kusur
sayısı dikkate alınarak analizler yapılır. Bu diyagramlarda herhangi bir ölçü aleti ile yapılan
ölçümler (nicelikler) değil, duyu organları ile ayırt edilebilen (görerek, duyarak, dokunarak
vs.) niteliksel değerlerin kontrolü yapılmaktadır.
Ölçülebilen özellikler için kullanılan kontrol diyagramları çok etkin kalite kontrol araçları
olmakla birlikte bazı durumlarda etkinliği zayıflamaktadır. Bir parçanın çok sayıda kalite
özelliği varsa, her biri için ayrı bir X , R veya S diyagramı oluşturmak gerekecektir. Oysa bu
özelliklerden herhangi birisi kontrol dışı olduğunda bu parça kusurlu kabul edilecekse o
zaman niteliksel kontrol diyagramlarının kullanılması çok daha uygun olacaktır.
Niteliksel değerler için aşağıdaki diyagramlar kullanılmaktadır.
•
Kusurlu oranı kontrol diyagramı (p kontrol diyagramı),
•
Kusurlu sayısı kontrol diyagramı (np kontrol diyagramı),
•
Kusur sayısı kontrol diyagramı (c kontrol diyagramı),
•
Birim başına düşen kusur sayısı kontrol diyagramı (u kontrol diyagramı)
Kusurlu Oranı ( p ) Kontrol Diyagramı
Bazı durumlarda bir ürünün kalitesi o ürünün kusurlu olup olmadığını belirlemek yoluyla
araştırılabilmektedir. Bu gibi durumlarda örneklerin kusurlu oranları yani p ile ilgili kontrol
diyagramları üreticilere yardımcı olmaktadır. Kusurlu oranları ile ilgilenildiğinde ana kütlenin
dağılımı Binom dağılımına uymakta, örnek oranlarının yani p’lerin örnekleme dağılımı ise n
yeterince büyük olursa ( n ≥ 30 ) normale yaklaşmaktadır. Bu durum p diyagramları için ± 3
standart hata ile belirlenen kontrol sınırlarının kullanılmasına imkan vermektedir.
8
İlgilenilen sürecin ya da ana kütlenin kusurlu oranı p iken, kusurlu oranının ortalaması ve
standart sapması sırasıyla
σp =
µ=p
p (1 − p )
‘dır.
n
Buna göre sürecin kusurlu oranı bilindiği taktirde, p kontrol diyagramının kontrol sınırları
ve orta çizgisi,
p(1 − p )
n
ÜKS p = p + 3
MÇ p = p
p(1 − p )
n
AKS p = p − 3
olarak tanımlanır.
Bazı durumlarda p önceden bilinemez ya da süreç için her hangi bir standart değer verilmezse,
bunun yerine örneklerden ortalama kusurlu oranı p ’nin hesaplanması gerekir. Süreçten
alınan örnek sayısı m ve i. örneğin kusurlu oranı ~
pi ise, örneklerin kusurlu oranlarının
ortalaması,
m
p=
∑ ~p
i =!
i
m
olur. p ´nın beklenen değeri,
E ( p) = p
olduğundan, kontrol diyagramında p yerine onun tahmini olan p
kullanılır. Bu durumda
sürecin kusurlu oranı bilinmiyor, örnekten elde ediliyorsa p kontrol diyagramına ait
limitler;
9
ÜKS p = p + 3
p (1 − p )
n
MÇ p = p
AKS p = p − 3
p (1 − p )
n
olarak yazılır.
Kusurlu birimlerin kontrolünde her zaman aynı büyüklükte örnekler alınamayabilir. Böyle
durumlarda örnekteki birim sayıları değişiklik gösterir. Bu yüzden diyagramın kontrol
sınırları için ortalama örnek büyüklüğü n ´nin kullanılması işlemlerde kolaylık sağlar.
Süreçten alınan örnek sayısı m ve i.örnekteki birim sayısı ni ise, ortalama örnek büyüklüğü,
m
n=
∑n
i =1
i
olur.
m
Diyagramın orta çizgisi p , süreç için standart bir p´ değeri verilmediğinde, örneklerde
belirlenen toplam kusurlu sayısının, toplam birim sayısına oranı olarak belirlenir. i. örnek
büyüklüğü ni ve kusurlu birim sayısı da d i ise, ortalama kusurlu oranı,
p=
∑d
∑n
i
i
olarak hesaplanır ve p kontrol diyagramının orta çizgisini oluşturur. Diyagramın kontrol
sınırları da
AKS p = p + 3
p (1 − p )
n
MÇ p = p
AKS p = p − 3
p (1 − p )
n
10
şeklinde yazılır.
Örnek 8.1. Elektrik prizleri üretimi yapan bir işletmede üretim hattından belli aralıklarda 200
ürün alınıp kontrol edilmiş ve kusurlu ürün sayıları aşağıdaki tabloda verilmiştir. Bu verileri
kullanarak kusurlu oranı (p) diyagramını oluşturarak sonuçları yorumlayınız.
Kusurlu sayısı
Örnek
Kusurlu
Örnek no
Kusurlu sayısı
Kusurlu oranı (p i )
oranı (p i )
no
1
10
0,05
11
10
0,05
2
8
0,04
12
8
0,04
3
7
0,035
13
9
0,045
4
9
0,045
14
13
0,065
5
15
0,075
15
12
0,06
6
11
0,055
16
6
0,03
7
8
0,04
17
8
0,04
8
17
0,085
18
12
0,06
9
13
0,065
19
10
0,05
10
14
0,07
20
7
0,035
Toplam
∑c
i
= 207
∑p
i
= 1,035
m
p=
∑p
i =!
m
i
=
1,035
= 0,05175
20
ÜKS p = p + 3
p (1 − p )
(0,05175)(0,94825)
= 0,05175 + 3
= 0,0987
n
200
MÇ p = p = 0.05175
11
p(1 − p )
(0,05175)(0,94825)
= 0,05175 − 3
= 0,0048
n
200
AKS p = p − 3
Kusurlu orani
p Diyagrami
0,10
ÜKS=0,0987
0,05
MÇ=0,05175
AKS=0,0048
0,00
0
10
20
Örnek no
Şekil 8.1. Kusurlu oranı (p) kontrol diyagramı
Kusurlu oranı açısından proses kontrol altındadır, herhangi bir düzeltici önlem almaya gerek
yoktur..
KATSAYILAR TABLOSU