r.R
ec
ep
D
im
itr
o
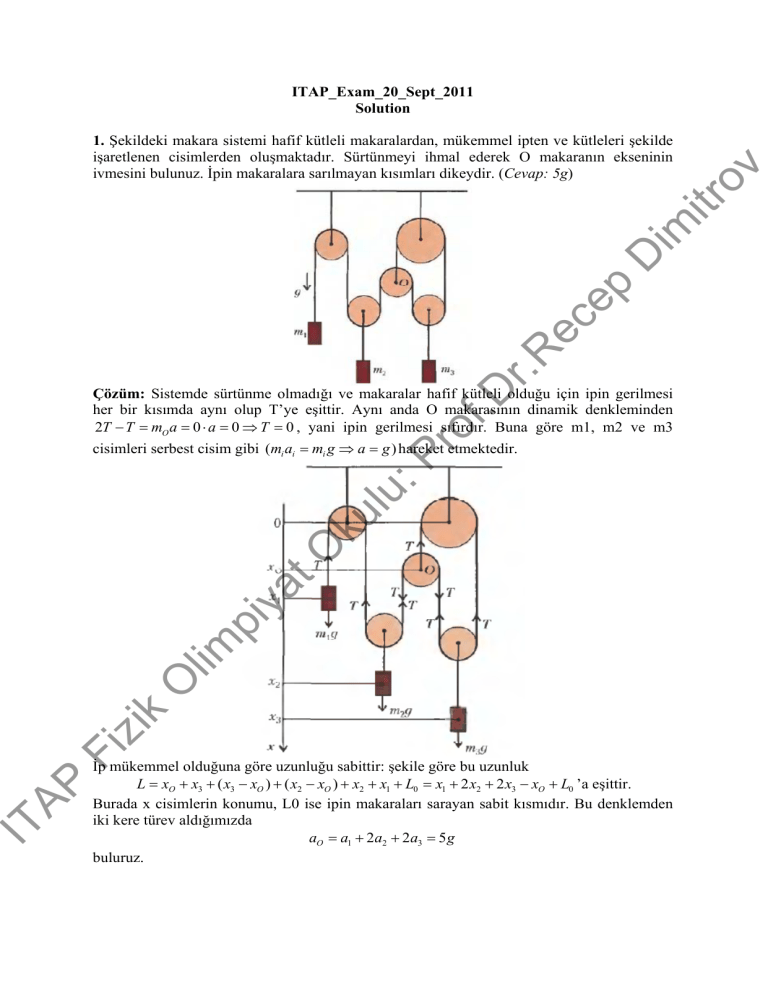
1. Şekildeki makara sistemi hafif kütleli makaralardan, mükemmel ipten ve kütleleri şekilde
işaretlenen cisimlerden oluşmaktadır. Sürtünmeyi ihmal ederek O makaranın ekseninin
ivmesini bulunuz. İpin makaralara sarılmayan kısımları dikeydir. (Cevap: 5g)
v
ITAP_Exam_20_Sept_2011
Solution
IT
AP
Fi
zi
k
O
lim
pi
ya
tO
ku
lu
:P
ro
f.D
Çözüm: Sistemde sürtünme olmadığı ve makaralar hafif kütleli olduğu için ipin gerilmesi
her bir kısımda aynı olup T’ye eşittir. Aynı anda O makarasının dinamik denkleminden
2T − T = mO a = 0 ⋅ a = 0 ⇒ T = 0 , yani ipin gerilmesi sıfırdır. Buna göre m1, m2 ve m3
cisimleri serbest cisim gibi (mi ai = mi g ⇒ a = g ) hareket etmektedir.
İp mükemmel olduğuna göre uzunluğu sabittir: şekile göre bu uzunluk
L = xO + x3 + ( x3 − xO ) + ( x2 − xO ) + x2 + x1 + L0 = x1 + 2 x2 + 2 x3 − xO + L0 ’a eşittir.
Burada x cisimlerin konumu, L0 ise ipin makaraları sarayan sabit kısmıdır. Bu denklemden
iki kere türev aldığımızda
aO = a1 + 2a2 + 2a3 = 5 g
buluruz.
Çözüm: Yay sabiti k olan bir dinamometre yayın uzamasını
(ξ ) okur
ve bu değeri
ep
kullanarak
D
im
v
itr
o
2. Bir okul laboratuar dinamometresi pürüssüz bir masa üstünde bulunmaktadır. Bu
dinamometre kütlesi M=0.5kg olan taşıyıcı bir tahtadan ve
kütlesi m=0.1kg olup tahtaya bağlanan, fazla sayıda özdeş
sarımlardan oluşan bir yaydan meydana gelmektedir
(şekildeki gibi). Dinamometrenin uçlarından birine, yayın
ekseni yönüde, büyüklüğü F=1N olan bir kuvvet
uygulanıyor. Bu durumda dinamometrenin ölçeceği kuvvetin büyülüğü nedir? Yayla destek
tahta arasındaki sürtünmeyi ihmal ediniz. (Cevap: kuvvet yayın tahtaya bağlanan ucuna
uygulanırsa 1/12N, kuvvet serbest uca uygulandığında 11/12N)
(3)
(4)
(5)
ya
tO
ku
lu
:P
ro
F2 − F1
⋅ λ dx ’e
m
eşittir.Aynı anda Hook yasasına göre
F
dξ
≡σ = E
.
S
dx
Buradan
dξ
d 2ξ
⇒ dF = SE 2 dx ,
F = SE
dx
dx
yani Denk(3) ve (5)’ten
dF = adm =
f.D
r.R
ec
f = kξ
(1)
Förmülüyle kuvveti gösterir (hesaplar). Yayın uçlarına iki farklı kuvvet uygulandığında
okunan kuvvet
F + F2
(2)
f = 1
2
eşittir (formülde kuvvetlerin mutlak değerleri alınmıştır, yönleri birbirine zıttır). Gerçekten,
kütlesi m, uzunluğu ise L olan bir yayın ( x, x + dx ) kısmına uygulanan net kuvvet
lim
veya
zi
k
O
dξ
= cx + c1 ,
dx
F
F
dξ
burada c1 ve c2 iki farklı sabittir. x = 0 iken ξ = 0 ve
= 1 yani sabitler için c1 = 1 ,
dx x =0 SE
SE
c2 = 0 buluruz ve sonuçta yayın uzaması konumun fonksiyonu olarak
1 F2 − F1 2 F1
ξ=
x +
x ’e
2 SEL
SE
eşittir. x = L iken
F
1 F2 − F1
1
1 f
⋅ L + 1 L = ( F1 + F2 ) ⋅ = ,
ξ=
2 SE
2
SE
k k
ES
yay sabitidir ve buradan denk.(2)’yi ispatlamış oluruz .
burada k =
L
Soruda yayın serbest ucuna F2 = F diğer ucuna ise F1 uygulandığında
Fi
AP
IT
F2 − F1
d 2ξ
d 2ξ F2 − F1
λ
dx
=
⋅
dx
⇒
=
=c
dx 2
m
dx 2
SEL
pi
dF = SE
1
2
ξ = cx 2 + c1 x + c2 ;
r.R
ec
ep
D
im
v
itr
o
F − F1
F
=a=
m
m+M
denklemi tahta-yay sistemin ivmesini veriyor, yani
M
F1 =
F.
m+M
Buradan,
M
+1
F1 + F2 m + M
11
f =
F = N.
=
2
2
12
F kuvvet tahtaya uygulandığında yaya tahtadan etki eden kuvvet F2 , diğer ucu ise serbesttir:
m
F ’e eşittir.
F1 = 0 ve F2 = ma =
m+M
Yani
F + F2
m F 1
f = 1
=
= N
2
m + M 2 12
lu
:P
ro
f.D
3. Düşey durumda bulunan kapalı bir silindirik kap ağır bir pistonla iki kısıma bölünmüştür.
Pistonun yapıldığı madde helyum gazını geçirirken havayı geçirmemektedir. Başlangıçta
kabın alt kısmında hava, üst kısmında ise miktarı havanın miktarının beşte biri olan helyum
gazı bulunmaktadır. Her iki bölmenin de hacmi V’dir ve piston dengededir. Sistem denge
durumuna gelene kadar piston yerini ne kadar değiştirmiş olacaktır? Pistonun kesit alanı S’ye
eşittir, sürtünme yoktur ve sistemin sıcaklığı devamlı sabit tutuluyor. (Cevap:V/4S)
O
lim
pi
ya
tO
ku
Çözüm: İlk anda silindirin iki bölümünde basınç farkı
n ⎞ RT 4 nRT
⎛
P1 − P2 = ⎜ n − ⎟
=
=P
5⎠ V
5 V
⎝
pistonun oluşturduğu basınca eşittir. Son durumda helyumun kısmi basıncı silindirin her bir
bölgesinde aynıdır ve pistonun dengesini sağlayan havanın kısmi basıncıdır:
nRT 4 nRT
=
= P.
Pair =
Vair
5 V
5
5
1
1V
Buradan, Vair = V ⇒ Vair − V = V − V = V ⇒ Δh =
4
4
4
4S
IT
AP
Fi
zi
k
4. Bir ‘kara kutu’ içerisinde, kutudan dışarıya çıkan uçlar arasında bulunan birkaç türdeş
direnç dışardan görülemeyen bir devre oluşturuyor. Kutunun
dışarıya çıkan 1 ve 2’ci uçları arasına gerilimi ε, iç direnci ise
düşük olan bir pil bağlanıyor. 3 ve 4’üncü uçlar arasına ideal
bir voltmetre bağlanıyor. Voltmetrenin sıfır noktası ölçüm
ekranının ortasındadır.
Verilen durumda voltmetre sıfır
gerilim göstermektedir. 1 ve 3’üncü veya 2 ve 4’üncü uçlar
arasında içerdeki dirençlere türdeş olan bir direnç bağlanırsa,
voltmetrenin okuduğu gerilim +U, 1 ve 4’üncü veya 2 ve
3’üncü uçlar arasında bağlanırsa –U olmaktadır. Kutu içinde bulunup bu durumu en az direnç
sayısıyla gerçekleştirebilecek devreleri çiziniz. U geriliminin değeri ne kadardır? (Cevap: 4
dirençli köprü devresi, U=ε/6; veya 4 dirençli ‘haç’ devresi U=ε/5)
r.R
ec
ep
D
im
itr
o
v
Çözüm: Dört çıkış noktası arasında bağlanan direnç sayısının minimum değeri 4 olabilir,
yani kutu içinde 4 direnç bulunmaktadır. Bu dirençleri ‘köprü’ veya ‘haç’ şekilleri olmak
üzere iki farklı şekilde bağlayabiliriz: (şekildeki gibi):
Köprü şeklinde voltmetrenin okuduğu gerilim: U = V4 − V3 , aynı anda
zi
k
O
lim
pi
ya
tO
ku
lu
:P
ro
f.D
⎧V1 = 0
⎪V = ε
⎪ 2
⎪
1
⎪V3 − 0 = R ε = 1 ε
⎨
R+R
2 ⇒U = 6ε
⎪
⎪V4 − 0 = R ε = 2 ε
R
⎪
3
R+
⎪⎩
2
‘Haç’ şeklinde R3 direncinden ve voltmetreden akım geçmemektedir: VO = V3 , haç şeklinin
kesişim noktasının ve 3. noktanın potansiyelleri aynıdır. Kirçoff yasalarına göre dirençlerden
geçen akımlar için
⎧i1 + i2 = 1
⎪
⎨i1 + i4 + i5 = 1
⎪i = i + i
⎩1 2 4
(hesapları kısa yazmak için ε = R = 1 alınmıştır) . i4 = i5 denkleminden akımları buluruz:
IT
AP
Fi
Buradan U = V4 − V3 = V4 − VO = i4 =
3
⎧
⎪i1 = 5
⎪
2
⎪
⎨i2 =
4
⎪
1
⎪
⎪i4 = i5 = 5
⎩
1
1
, boyutlu şekilde ise U = ε
5
5
5. Dikey silindirik bir bardakta kırılma indisi n=1.5 olan viskoz bir sıvı bulunmaktadır.
Yukarıdan bardağa şiddeti sabit olan düşey paralel ve ince bir ışık demeti düşmektedir. Sıvı
ile dolu olan bardak, ω=1s-1 açısal hızına kadar hızlandırılıyor ve bu durumda silindirin
ekseninde sıvının yüksekliği h=30cm’ye eşit oluyor. Bardağın dibindeki merkez noktasının
etrafındaki bölgeye düşen ışığın şiddetinin değeri ne kadar değişecektir? Yer çekim ivmesini
g=10m/s2 olarak alınız, sıvı içinde ise ışığın soğurulmasını ve yansımasını ihmal ediniz.
(Cevap: %2)
ep
D
im
itr
o
v
Çözüm: Sıvının yüzeyinde kütlesi dm olan küçücük bir sıvı miktarın dengesini ω açısal hızı
ile dönen eylemsiz olmayan referans sisteme göre inceleyelim (şekildeki gibi):
IT
AP
Fi
zi
k
O
lim
pi
ya
tO
ku
lu
:P
ro
f.D
r.R
ec
dmg + dmω 2r + N = 0 .
Burada dmg , dmω 2r ve N sırasıyla yer çekim, eylemsiz merkez-kaç ve cisme sıvıdan
uygulanan kuvvetlerdir. Üç kuvvetin toplamı sıfır iken sinüs teoremine göre
dmg
dmω 2 r
ω 2r
=
⇒ tan α =
.
g
⎛π
⎞ sin (π − α )
sin ⎜ + α ⎟
⎝2
⎠
Açı α küçük olduğuna göre
ω 2r
α≈
.
g
Aynı anda bu açı düşen ışığın sıvının yüzeyinle arasındaki açıdır, dolayısıyla kırılma açısı
α ω 2r
β= =
.
n ng
Buradan ışık demetin sapma açısı için
α ⎛ 1 ⎞ ω 2r
γ = α − β = = ⎜1 − ⎟
n ⎝ n⎠ g
buluruz.Tanım olarak ışığın şiddeti birim zamanda birim alan enerji ir, dolayısıyla şiddetin
bağıl değişimi
P P
−
I 0 − I S0 S S − S0 r 2 − r02 2Δr 2γ h
δ=
=
=
=
≈
=
,
P
I0
S
r2
r
r
S0
burada Δr silindirin dibinde demetin yarıçapın artışıdır. Dolayısıyla,
2
2γ h
⎛ 1 ⎞ω h
δ=
= 2 ⎜1 − ⎟
.
r
⎝ n⎠ g
2
⎛ 1 ⎞ω h
Verilere göre δ = 2 ⎜1 − ⎟
≈ 0.02 = 2%
⎝ n⎠ g