Chua Devresinin Gerçeklenmesi ve Simülasyonu

6th International Advanced Technologies Symposium (IATS’11), 16-18 May 2011, Elazığ, Turkey
Chua Devresinin Gerçeklenmesi ve
Simülasyonu
V. Yamaçlı1, K. Abacı2 ve E. Köse3
1
Mersin Üniversitesi, Turkey, vyamacli@gmail.com
2
Mersin Üniversitesi , Turkey, kabaci@gmail.com
3
Mersin Üniversitesi , Turkey, ercankos@gmail.com
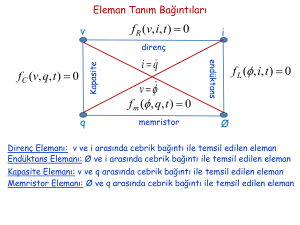
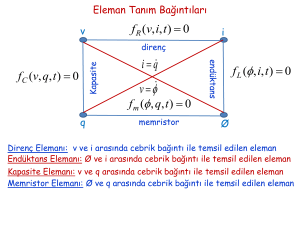
elemanlarının uç bağıntıları yerine yazılırsa devrenin durum
denklemleri elde edilir. Bu durum denklemleri basit bir analik işlemle
durum uzay formuna getirilir. Çalışmanın ikinci bölümünde bu
analizler yapılmıştır.
Bu çalışmada kullanılan Chua devresinin doğrusal olmayan devre
denklemleri durum uzay formuna getirilerek MATLAB/SIMULINK
ortamına taşınmıştır. Doğrusal olmayan Kaotik davranışları
incelemek, değişen sistem dinamikleri ve doğrusal olmayan sistem
elemanları nedeniyle pek kolay değildir. Sistemdeki kaotik davranışın
analizi için, sistem durum uzay modelinin en az üç boyutlu olması
gerekir[1]. Çalışmada kullandığımız devrenin MATLAB/SIMULINK
ortamında gerçekleştirilen tasarımı ile durum değişkenlerine ait
cevaplar elde edilmiştir. Aynı devre elektronik devre elemanları
kullanılarak laboratuar ortamında gerçekleştirilmiş ve elde edilen
sinyal cevapları karşılaştırılmıştır.
Realization and Simulation of Chua’s Circuit
Abstract— In order to describe practical chaotic systems exactly,
we presented a simple modified Chua’s circuit. The systems
which have nonlinear components become more complicated
when other components based on derivative or integral added. In
this paper, this kind of circuit known as Chua’s Circuit is
mathematical analysed and subsequent to results it is simulated in
MATLAB™. Chua oscillator has several linear components, but
has also a non-linear component that is known as Chua’s diode. It
is shown how to generate a sequence of chaotic behaviors by
varying the value of a linear resistor. The results are displayed in
the form of MATLAB generated graphics. Results of simulation
and realization of the circuit are compared and presented.
Keywords—Chua’s Circuit, Chaos
Equations, Chaos’ Circuit Simulation
State,
State-Space
II. CHUA DEVRESİNİN ANALİZİ
Şekil 1‘de Chua Devresi görülmektedir. Kutu içerisindeki kısım
doğrusal olmayan negatif bir dirençtir ve Chua diyodu olarak bilinir.
Chua devresinde görülen C1, C2 kapasitörleri ve L indüktörü üç
boyutlu bir durum uzay denklemini sağlamaktadır.
I. GİRİŞ
ON yıllarda, kompleks sistem dinamiklerinin analizi ve kontrolü
doğrusal olmayan elemanlar üzerine çalışan bilim dalının temel
konularından biri haline gelmiştir. Doğrusal olmayan sistemlerin
içinde bulundukları karmaşık durum kaos durumu olarak
nitelendirilir. Kaotik davranış, çok basit ve küçük boyutlu bir
doğrusal olmayan sistem de olsa her yerde oluşabilir. Son yirmi yıl
boyunca, dinamik sistemlerde deterministik kaosa olan ilgi
artmıştır[1]. Kaos teorisi en başta fizik ve matematik olmak üzere
birçok bilim dalı literatüründe yerini almıştır[2]. Kaos sistemi ayrıca
lazerlerin gücünün artırılmasında, elektronik devrelerin çıkışlarının
senkronize edilmesinde, kimyasal reaksiyonların osilasyon
kontrolünde, beyin dalgalarının incelenmesi ve görüntü sıkıştırma ve
iletilmesi gibi birçok farklı ve yaygın kullanım alanı vardır[3-5]. Bu
nedenle pratik olarak birçok model, kaotik davranışın incelenmesi
için önerilmiştir[6-8]. Elektronik devrelerde, uygulama ve sinyal
ölçümü kolay olduğundan kaos çalışmak oldukça elverişlidir.[9]
S
Şekil 1: Chua Devresi
A. Doğrusal Olmayan Devre Elemanı Analizi
Negatif direnç çok basit bir konsepttir. Şekil 2‘de verilen işlemsel
yükselteç devresi için sanal toprak kanunu ve kirchoff yasaları
kullanılarak (1) - (4) denklemleri yazılabilir.
Elektronik devre alanında kaos durumu ilk kez Leon Chua tarafından
incelenmiştir. Chua konuyu en basit şekliyle ele almak amacıyla
Chua devresini tasarlamıştır[5]. Chua devresi, kaos ve çatallaşmanın
gösterilmesi için. basit ve tipik üçüncü mertebeden otonom bir
devredir Son yıllarda, bir çok Chua devresi gerçekleştirilmiştir
[10-17]. Chua devresi ile özellikle senkronizasyonu kullanılarak
güvenli haberleşme alanında ve pratik kaotik sistemleri açıklamak
gibi çok önemli çalışmalar mevcuttur[18-20].
MATLAB bir elektronik yazılım programı olmamasına rağmen kısmi
diferansiyel denklemleri çözmek için çok güçlü bir araçtır. Kirchoff
kanunları kullanarak elde edilen devre denklemlerinde Chua devresi
Şekil 2: İşlemsel Yükselteç
82
Chua Devresinin Gerçeklenmesi ve Simülasyonu
I2 
Vs
(1)
I NR
Rg
Vs  Ra I1  I 2 ( Rb  Rg )
Vs  ( I1 Ra )
Rg
(2)
 g 2VC1  ( g1  g 2 ) BP1VC1   BP1,

  g1VC1  BP1  VC1  BP1,
 g V  ( g  g ) BP1V   BP1
2
1
C1
 2 C1
(3)
g1  
(4)
g2 
Rb
Rg
Vs
  Ra
I1
Rb
1
Rp
(8)
(8.1)
( R p  R2 )
(8.2)
R p R2
(4)‘te görülen eşdeğer giriş direnci gerçekten negatif direnç etkisi
gösterir.
(8) ifadesi, (5)‘de yerine yazılır ve durum uzay eşitliği aşağıdaki gibi
belirlenir,
B. Chua Devresinin Durum Uzay Modeli
 x   A x   Bu 
Şekil 3‘te bir direnç (R), iki kapasite (C1), (C2) bir bobin (L) ve Chua
diyodundan oluşan üçüncü mertebeden basit otonom bir kaotik devre
görülmektedir. Devre teorisi uygulanarak (5) - (7) eşitlikleriyle
verilen durum denklemleri elde edilir. (5) numaralı denklemde (iNR)
Chua diyodundan geçen akımdır.
(9) eşitliği kullanılarak doğrusal olmayan direnç karakteristiğine göre
her bölgedeki durum uzay eşitlikleri aşağıdaki şekilde elde edilir.
Elde edilen (10) – (12) ifadeleri kısmi diferansiyel denklem setidir.
g
1
 1
 2

VC1   RC1 C1 RC1
   1
1

VC 2   
RC
RC
2
i   2
L  
1

0
L

Şekil 3‘te verilen devre için durum denklemleri aşağıdaki gibi
yazılabilir,
(5)
dVC 2 VC1 VC 2
i


 L
dt
RC2 RC2 C2
(6)
V
diL
  C2
dt
L
(7)

0 
 ( g 2  g1 ) BP1 

 VC1  
C1

1   

VC1   BP1,
0
 VC 2 
C2    

iL  
0




0 

g1 1
 1
  RC  C RC
1
1
1
VC1  
   1
1

VC 2   
RC2
i   RC2
L  
1

0
L

Şekil 3: Chua Devresinin Basit Gösterimi
dVC1 VC 2 VC1 iNR



dt
RC1 RC1 C1
(9)
g2 1
 1
  RC  C RC
1
1
1
VC1  
   1
1

VC 2   
RC2
i   RC2
L  
1

0
L


0 
 VC1 
1  
 VC 2  BP1VC 1  BP1,
C2   
i 
 L 
0 


0 
 ( g1  g 2 ) BP1 

 VC1  
C1

1   
VC1  BP1,
0
 VC 2  
C2    

iL  
0





0 


… (10) (11) (12)
Chua devresindeki diyotlar da göz önüne alınarak Şekil 4‘te görülen
doğrusal olmayan negatif direnç karakteristiği elde edilir.
III. CHUA DEVRESİNİN SİMÜLASYONU
Chua devresinden elde edilen kısmi diferansiyel denklem sonuçlarını
çözümlemek kolay değildir. MATLAB çok güçlü bir çözümleyicidir.
Chua diyoduna ait parçalı I-V karakteristiğinin formulasyonları
denklem 10 - 12‘de verilmiştir. Şekil 5‘de bu formulasyonun
SIMULINK modeli gösterilmiştir. Çalışmada sistemin durum uzay
denkleminin simülasyon ortamında doğru bir şekilde çözülebilmesi
için, kullanılan çözüm metodu ode23t olarak en uygun şekilde
seçilmiştir. Değişik direnç değerleri için yapılan çalışmalarda
sistemin verdiği tepkilerin simülasyon ortamında gözlenebilirliği
görülmektedir. Simülasyonda kullanılan devre elemanlarına ait
parametre değerleri Şekil 1‘deki değerlerle aynıdır. Gerekli diğer
veriler Ek A‘da mevcuttur.
Şekil 4: Doğrusal Olmayan Negatif Direnç Karakteristiği[21]
Burada g1 ve g2 sırasıyla dış ve iç bölge eğimlerini, ± BP1 ise kırılma
noktalarını gösterir.
83
Chua Devresinin Gerçeklenmesi ve Simülasyonu
Out1 In 1
Subsystem
Out1 In 1
Subsystem 1
-C-
1/u
C1
1/C1
-C-
1/u
C2
1/C2
y
V _C2
-CR
1/u
1/R
Vc1
1
s
x
1
s
V _C1
Vc2
1
s
iL
z
i_L
-C-
-1/u
L
1/L
Şekil 5: Simulink dosya şeması
Şekil 5 incelendiğinde, 10 - 12 durum uzay denklemleri kullanılarak
oluşturulan Simulink sistemi olduğu görülebilir. Şekil 5‘deki
Subsystem bloğu, eşitlik 9‘da verilen durum uzay denklemleri A
matrisindeki g1 ve g2 için bir seçme sistemi, Subsystem1 ise yine
durum uzay denklemleri B matrisindeki g1ve g2 fark değerlerinin
seçilmesi için oluşturulmuş bir seçme sistemidir. Subsystem yapısı
Şekil 5.1‘de verilmiştir
1
VC1 [volt]
0.5
0
-0.5
-1
0
0.5
1
1.5
zaman [s]
2
-5
x 10
(a)
0.5
0.55 E-3
g1
Switch 2
VC2 [Volt]
1
Switch 1
Out 1
1
In 1
0
-0.5
0
0.5
1
1.5
2
2.5
zaman [s]
3
-3
x 10
(b)
2.47 E-3
-3
g2
2
iL [Amper]
Şekil 5.1: Simulink Şeması – Subsystem Yapısı
Şekil 5.1‘de Simulink şemasındaki Subsystem yapısı görülebilir.
Switchler kullanılmak suretiyle VC1 değeri ±BP1 ile karşılaştırılır, A
matrisindeki g1 veya g2 değişkenlerinden birisi seçilir ve simülasyon
Şekil 4‘deki doğrusal olmayan negatif direnç karakteristiğine göre
çalışmaya devam eder.
x 10
0
-2
0
0.5
1
1.5
zaman [s]
2
2.5
3
-3
x 10
(c)
Şekil 6‘da durum değişkenlerinin zamana göre değişimleri
görülebilir. Osilasyonların grafiklerde daha net görülebilmesi
amacıyla çizim aralıkları en uygun şekilde seçilmiştir..
Şekil 6: a) VC1, b) VC2 ve c) iL değerlerinin zamana göre değişimleri,
R = 1.65K
84
Chua Devresinin Gerçeklenmesi ve Simülasyonu
Şekil 7‘de R=1.65 K için durum değişkenleri iL ve VC2‘ ye ait faz
diyagramları çizdirilmiştir.
Şekil 8 ve Şekil 10 karşılaştırıldığında VC1 ve VC2 durum değişkenleri
arasındaki
kaotik
davranışların
benzer
yapıda
olduğu
gözlemlenmiştir.
Rp bir önceki simülasyon çalışmasındaki değerinde sabit tutularak R
direncinin farklı değerleri için yapılan simülasyon çalışmaları
sonucunda elde edilen durum uzay diyagramları Şekil 8 ve 9‘da
çizdirilmiştir.
Şekil 9‘da Chua devresinin simülasyonu sonucunda elde edilen çift
çekerli görüntüler laboratuvar ortamında elde edilmeye çalışılmıştır.
Mevcut şartlarda birtakım fiziksel nedenlerden dolayı bazı gürültüler
içermektedir. Buna ait görüntüler Şekil 11‘de verilmiştir. İki şekil
karşılaştırıldığında benzerlikler görülebilir. Şekil 12‘de direnç değeri
artırıldığında çoklu kaotik çekerler oluştuğu gözlemlenmiştir
0.8
0.6
VC2 [Volt]
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-2
-1.5
-1
-0.5
0
0.5
1
iL [Amper]
1.5
2
-3
x 10
Şekil 7: iL ve VC2 değişimleri, R = 1.65K
R değeri Şekil 8‘de 1.78K ve Şekil 9‘da ise 1.82K seçilerek durum
değişkenleri VC1 ile VC2 arasındaki faz diyagramları çizdirilmiştir. R
direncinin
değeri
arttırıldığında
yörüngelerin
birbirinden
uzaklaşmaya başladığı ve artan genlikte osilasyonların oluştuğu
gözlemlenmiştir.
-3
1
x 10
VC2 [Volt]
0.5
Şekil 10: X-Y Modunda Gözlenen VC1 – VC2 değişimleri
0
-0.5
-1
-2
0
2
4
6
8
VC1 [Volt]
10
-3
x 10
Şekil 8: VC1 ve VC2 değişimleri, R = 1.78K
30
VC2 [Volt]
20
10
0
-10
-20
-15
-10
-5
0
5
10
15
VC1 [Volt]
Şekil 9: VC1 ve VC2 değişimleri, R = 1.82K
IV. CHUA DEVRESİNİN GERÇEKLEŞTİRİLMESİ
Çalışmanın bu bölümünde Rp = 1.8K sabit kalmak kaydı ile
R = 1.78K seçilerek Şekil 1‘de verilen devredeki VC1 ve VC2
arasındaki davranışı gözlemlemek için laboratuar ortamında bir deney
düzeneği hazırlanmıştır. Deney sonucunda devrenin davranışı Şekil
10 - 12 ‗de görülen osiloskop ekranından izlenilebilir.
Şekil 11: X-Y Modunda Gözlenen VC1 – VC2 değişimleri
85
V. Yamaçlı, K. Abacı, E. Köse
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
Şekil 12: X-Y Modunda Gözlenen VC1 – VC2 değişimleri
[11]
[12]
V. SONUÇLAR
Chua devresinin simülasyon ve deneysel sonuçları elde edilmiştir.
Simulasyon sonuçları ile (Şekil 8-9) deneysel sonuçların birbirine
benzer olduğu gösterilmiştir (Şekil 10-11). Simülasyon sonuçlarında
görüldüğü gibi, R değeri 2K değerine yaklaştığında sistem kaos
durumunun son aşamasına gelmektedir ve bir noktadan sonra
sistemin gerilim ve akım değerleri aşırı miktarda artmaktadır..
Buradan anlaşılacağı üzere kritik nokta aşıldıktan sonra sistem
girişindeki çok küçük değişimler dahi çıkışta çok büyük
değişikliklere yol açmaktadır. R = 1.78K için simülasyon sonuçları
ve devrenin gerçeklenmesi ile elde edilen sonuçlar karşılaştırıldığında
simülasyon ile elde edilen sonuçların gerçek sonuçlara benzer olduğu
anlaşılmıştır. Kritik noktadan sonra devre
kaotik yapıya
büründüğünden meydana gelen
aşırı değişimlerin, pratikte
gerçeklenen sistemde gözlenmesi fiziksel devre elemanları nedeniyle
mümkün olamamıştır. Daha hassas ölçüm cihazları ve aparatlarının
kullanılması Osilaskop görüntülerinin daha net görülebilmesi için
avantaj sağlayacaktır.
[13]
[14]
[15]
[16]
[17]
[18]
[19]
EK-A
[20]
Tablo 1: Doğrusal Olmayan Karakteristik Değerleri
BP1
0.11 V
BP2
0.4 V
g1
-0.55E-3
[21]
g2
-2.47E-3
Tablo 2: C1, C2, L için Başlangıç Koşulları
VC1
10E-3 V
VC2
0V
iL
0A
KAYNAKLAR
[1]
[2]
Pehlivan, İ. ve Uyaroğlu, Y., ―Sprott_94_A Kaotik Sisteminin
Senkronizasyonu ve Bilgi Gizlemede Kullanılması‖, Uluslararası
Katılımlı Bilgi Güvenliği ve Kriptoloji Konferansı, 2007, sf.230237.
Madan, R. N. and Wu C. W., Chua’s Circuit : A Paradigm of
Chaos, World Scientific Series on Nonlinear Science, 1993.
86
Ditto, W.L. and Pecora, L.M., ―Mastering Chaos‖, Scientific
American, 1993, pp.78–84.
Uçar, A., Türk, M. ve Ata, F., ―A Practical Realization of Chaos
Synchronization For Transmitting Information‖, The 32nd
International Scientific Symposium of the Defense Research
Agency, vol.4, Bucharest–Romania, 2001, pp.81-88.
Türk, M. ve Ata, F., ―Performance Analysis of Adaptive
Controllers on Chaotic Parameter Modulation and Variant
Channel Gain‖, 1st IEEE International Conference on Circuit and
System for Communication, ICCSC‘02, 2002, St. Petersburg,
Russia.
Sparrow, C.T., ―Chaotic Behavior in a 3-Dimensional Feedback
System‖, Journal of Mathematical Analysis and Applications,
1981, vol.83, pp.275-291
Kennedy, M. P., ―Experimental Chaos from Autonomous
Electronic Circuits‖, Phil. Trans. R. Soc. Lond. A., 1995, vol.353,
pp.13-32
Türk, M. ve Gülten A., ―Doğrusal Olmayan Elektronik Devrelerin
Bond Graf ile Modellenmesi‖, Sakarya Üniversitesi Fen Bilimleri
Enistitüsü Dergisi, 2002, vol.6, no.1, Mart.
Matsumoto T.A, ―Chaotic attractor from Chua‘s circuit. ‖IEEE
Trans Circuits Syst,1984, 31(12):pp.1055-1058
Sharkovsky A N. ―Chaos from a time-delayed Chua‘s circuit‖.
IEEE Trans Circuits Syst, 1993, 40(10): 781-783
Suykens J, Vanderwalle J. ―Generation of n-double scrolls
(n=1,2,3,4..)‖. IEEE Trans Circuits Syst, 1993, 40(10): 861-867
Torres L A B, Aguierre L A. ―Inductorless Chua‘s Circuit‖. IEE
Electro Lett, 2000, 36(23): 1915-1916
Yalcin M E, Suykens J A K, Vanderwalle J. ―Experimental
Confirmation of 3- and 5- scroll attractors from a generalized
Chua‘s Circuit circuit―. IEEE Trans Circuits Syst, 2000, 47(3):
425-429
Wang X F, Zhong G Q, Tang K S. ―Generating chaos in Chua^s
circuit via time delay feedback‖. IEEE Trans Circuits Syst, 2001,
48(9): 1151-1156
Tang W K S, Zhong G Q, Chen G. ―Generating of n-scroll
attractors via sine function‖. IEEE Trans Circuits Syst, 2001,
48(11): 1369-1372
Zou Y L, Zhu J. ―Generating the chaotic n-scroll Chua‘s circuit
with two low pass filters‖. Chaos Solutions and Fractals, 2006,
29(2): 400-406
Recai K. ―Mixed-Mode chaotic circuit with Wien-bridge
configuration: The results of experimental verification‖. Chaos
Solutions and Fractals, 2007, 30(5): 1188-1193
Agiza H N, Matouk A E. ―Adaptive synchronization of Chua‘s
circuit with fully unknown parameters‖. Chaos Solutions and
Fractals, 2006, 29(4): 219-227
Li C P,Yan J P. ―The synchronizaton of three fractional
differential systems‖. Chaos Solutions and Fractals, 2007, 30(4):
751-759
Yan J J, Yin J S, Liao T L. ―Synchronizaton of a Modified Chua‘s
circuit system via adaptive sliding model control‖. Chaos
Solutions and Fractals, 2006, 29(7): 1-8
E, Tlelo-Cuautle, Jesus M. Munoz-Pacheco., ―Simulatiıon of
Chua‘s Circuit by Automatic Control of Step-Size‖, Applied
Mathematics and Computation, 190, pp.1526-1533, 2007.