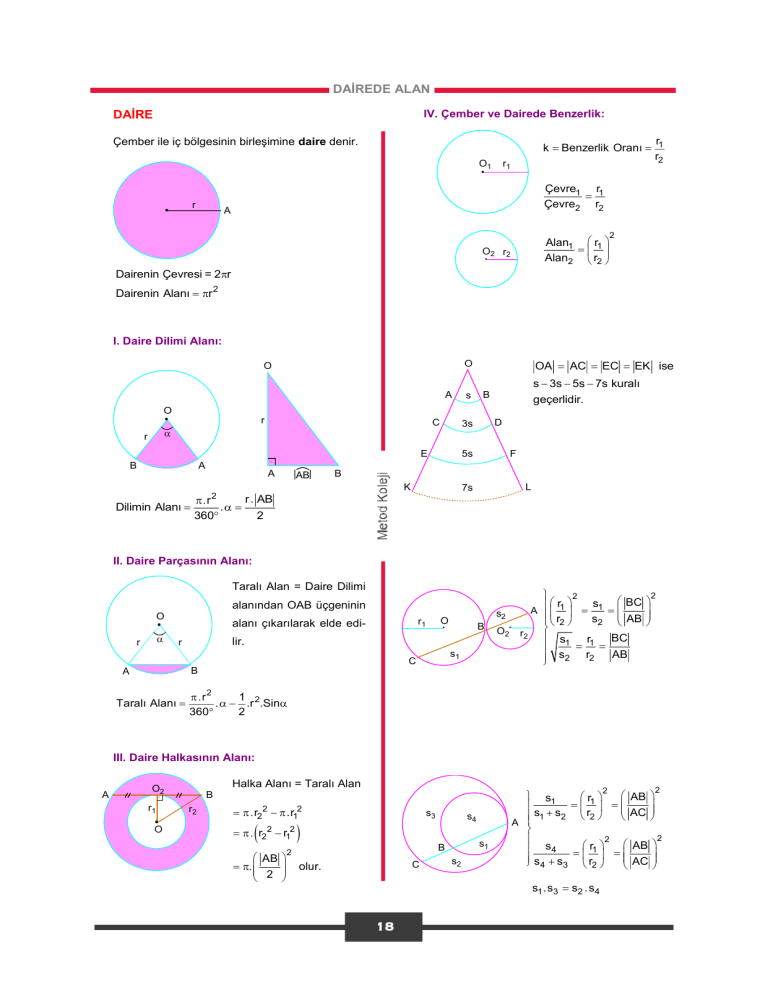
DAİREDE ALAN IV. Çember ve Dairede Benzerlik: DAİRE Çember ile iç bölgesinin birleşimine daire denir. k Benzerlik Oranı O1 r r1 r1 r2 Çevre1 r1 Çevre2 r2 A Alan1 r1 Alan2 r2 O 2 r2 2 Dairenin Çevresi = 2r Dairenin Alanı r 2 I. Daire Dilimi Alanı: O A O OA AC EC EK ise s s 3s 5s 7s kuralı geçerlidir. B O r C r E A B A AB D 3s 5s F B K L 7s r . AB r 2 Dilimin Alanı . 360 2 II. Daire Parçasının Alanı: Taralı Alan = Daire Dilimi alanından OAB üçgeninin O r alanı çıkarılarak elde edi- s2 O r1 B lir. r s1 C O2 2 BC s r1 A 1 AB r s 2 2 r2 s1 r1 BC AB s2 r2 2 B A Taralı Alanı r 2 1 . .r 2.Sin 360 2 III. Daire Halkasının Alanı: A Halka Alanı = Taralı Alan O2 r1 O 2 B r2 r22 .r12 r2 r12 2 AB 2 s3 s4 s1 B 2 C olur. s2 s1 .s3 s2 .s4 18 2 AB s1 r 1 AC s s r 1 2 2 A 2 2 s4 r1 AB AC s s 4 3 r2 DAİREDE ALAN A S5 S1 S4 S2 [BC], [AC] ve [AB] Örnek 71 yarım çemberlerin A m(ABC) 15 çapları ve S3 m(BAC) 90 ise B C Şekildeki dairenin yarıçapı 4 3 cm C 15o B O S3 = S1 + S5 dir. olduğuna göre, taralı alan kaç cm2 dir? A [AB], [AC] ve [BC] S2 S1 B S3 S5 S4 yarım C çemberlerin çapı ve m(BAC) 90 S6 Örnek 72 [AC, O merkezli çembere C ise m(ABC) S6 S2 dir. A 1 noktasında B teğettir. O Örnek 69 A, B, O doğrusal O1 ve O2 merkezli AB 1 cm C daireler A noktasında A O2 AC 3 cm ise teğettir. O1 taralı bölgenin alanı kaç cm2 dir? O1 O2 2 cm Taralı alan 20 olduğuna göre, O1 merkezli dairenin yarıçapı kaç cm dir? Örnek 73 O yarım dairenin C Örnek 70 merkezi O merkezli yarıçapı 6 O 30o A m(CAB) 60 4 cm olan dairede, AC 4 cm m(OAB) 30 60o A O B Yukarıdaki verilere göre, taralı alan kaç cm2 dir? B Yukarıdaki verilere göre, taralı alan kaç cm2 dir? 19 19 DAİREDE ALAN Örnek 74 Örnek 77 A 6 D A O çeyrek dairenin merkezi AO CD E C D AC OC 6 3 2 B F CD 6 3 cm C B O Şekildeki ABCD dikdörtgeninin içine B ve C merkezli Yukarıdaki verilere göre, taralı alan kaç cm2 dir? F noktasında birbirine teğet çeyrek daireler çizilmiştir. AD 6 cm, CE 2 cm dir. Buna göre, çeyrek dairelerin alanları toplamı kaç cm2 dir? Örnek 78 C O merkezli yarım dairenin yarıçapı 3 cm dir. Örnek 75 A daire içine [AO] ve B O O B Buna göre, taralı alanlar toplamı kaç cm2 dir? [OB] çaplı yarım A m(AOC) 80 80o O merkezli yarım daireler çizilmiştir. Taralı alan 8 cm2 dir. Yukarıdaki verilere göre, taralı bölgenin çevresi kaç cm dir? Örnek 79 ABC dik üçgen A 1 Örnek 76 B ve C çember 3 yaylarının merkezleri E C D O merkezli çeyrek B BF FC dairede, AE 1 cm BH OA AD 3 cm OH HA 4 cm B F C Yukarıdaki verilere göre, taralı alan kaç cm2 dir? O 4 H 4 A Yukarıdaki verilere göre, taralı alan kaç cm2 dir? 20 20 DAİREDE ALAN Örnek 80 Örnek 83 A K Şekilde O merkezli Şekildeki O merkezli yarım daire ile ABC dairelerin alanları dik üçgeni verilmiştir. farkı 48 cm2 dir. Taralı alanlar eşit olduğuna göre, IABI [AB], T noktasında O A x uzunluğunun küçük çembere teğet B T x m(AKB) 240 yarıçapa oranı C kaçtır? B O Buna göre, AC CB x kaç cm dir? C Örnek 81 B Örnek 84 [AB] ve [CD] yarıçapları 2 cm A D ve 6 cm olan dairelerin dış teğetleridir. S1 S2 D 20o C A Yukarıdaki şekilde daireler dıştan teğet olduğuna göre, taralı alanlar toplamı kaç cm2 dir? O B C Şekilde O merkezli 20 lik daire dilimi ve [AB] çaplı yarım dairede, S1 ve S2 bulundukları bölgenin S1 alanları, IOBI = IBCI olduğuna göre, oranı S2 kaçtır? Örnek 82 O noktası dairelerin merkezi [AC], B Örnek 85 noktasında küçük O daireye teğet A B C D O merkezli yarım C daire içine çevresi 12 AC 4 2 cm cm olan DOEC karesi çizilmiştir. Yukarıdaki verilere göre, taralı alan kaç cm2 dir? A O E B Yukarıdaki verilere göre, taralı alanların toplamı kaç cm2 dir? 21 21 DAİREDE ALAN Örnek 86 Örnek 89 O noktası dairelerin S1 O C A 120o S2 D merkezi, D B m(AOB) 120 ve S1 8 ise; S2 5 O merkezli çemberde C OD DC OD AB OD DC A dairelerin yarıçapları oranı kaçtır? 4 2 O B OA 4 2 cm Yukarıdaki verilere göre, taralı alan kaç cm2 dir? Örnek 87 D C ABCD kare B, D çeyrek çemberlerin merkezidir. Örnek 90 AB 8 cm A 8 A O merkezli daire ve OAB dik üçgen C B Yukarıdaki verilere göre, taralı alan kaç cm2 dir? teğet noktası 16 m(AOB) 90 C O AC 16 cm CB 4 cm 4 Örnek 88 D B C Yukarıdaki şekilde [AB] daireye C noktasında teğet olduğuna göre, taralı alanlar toplamı kaç cm2 dir? ABCD karesinin içine dört yarım daire çizilmiştir. Karenin bir kenarı 4 cm olduğuna göre, A B taralı alanlar toplamı kaç cm2 dir? 22 22 DAİREDE ALAN Örnek 91 A Örnek 93 D O O noktası ABCD Dıştan teğet eş karesinin iç teğet çemberinin merkezi B çemberlerin yarıçapları 3 2 ve D çeyrek birimdir. çemberlerin merkezi BC 2 2 cm B Yukarıdaki verilere göre, taralı bölgenin alanı kaç C Yukarıdaki verilere göre, taralı alan kaç cm dir? 2 birimkaredir? Örnek 94 A, B, C merkezli eş Örnek 92 B A S1 = 50 cm2 S1 C BB S2 çemberler birbirlerine dıştan teğettir. S2 = 18 cm2 C AC 16 cm Yukarıdaki şekilde eş çemberlerin yarıçapları 2 cm olduğuna göre, taralı alanların toplamı kaç cm2 A Yukarıdaki şekilde çemberler B noktasında dıştan teğet olduğuna göre, BC kaç cm dir? dir? 23 23 DAİREDE ALAN Örnek 95 Örnek 97 Çiftlikteki bir at sahibi eğitmek için 20 x 10 m2 A S1 60 S2 boyutlarında dikdörtgen şeklindeki bir çitle çevrili 15 8 bölgenin B köşesine A B B C bağlıyor. At saat yönünde ilerliyor. Atın ABC bir dik üçgen 20 AB AC bağlı olduğu ipin uzunluğu 60 m olup ip C AB 15 cm 10 gergin tutuluyor. Atın dolaşırken oluşturduğu alan kaç m2 dir? AC 8 cm Yukarıdaki şekilde [AB], [AC] ve [BC] çaplı yarım daireler verildiğine göre, S1 + S2 kaç cm2 dir? Örnek 98 ABC bir üçgen Örnek 96 AB AC A ve B çemberlerin B merkezleri D AD BD m(ABC) 60 BD DC 6 m A Yukarıdaki şekilde köşeleri A, B, C olan üçgen Yukarıdaki şekilde B merkezli çember, A merkezli şeklinde duvarla çevrilmiş bahçenin D noktasına çemberin 10 m uzunluğundaki bir iple bağlanan bir ineğin otlayabileceği alan en çok kaç m2 dir? iç bölgesinde dönerek başladığı noktaya kaç tur atarak gelir? 24 24 DAİREDE ALAN Örnek 99 Örnek 102 Şekildeki çemberler C K A dörtgeni 4 3 noktalarında teğettir. M AD DC x m(KCM) L BC 5 cm D m(KAL) CD 11 cm B m(MBL) 11 5 B AD 4 3 cm C Yukarıdaki verilere göre, AB= x kaç cm dir? Yukarıdaki verilere göre, + + kaç derecedir? Örnek 103 Örnek 100 A ABCD kirişler A birbirlerine K, L, M AC ve [BD] iki B 3 C A çembere teğet 4 C, D, E doğrusal D 2 5 O BC 3 cm 3 DC 4 cm E P 2 C K E O merkezli çemberde, [PA çembere A noktasında Yukarıdaki verilere göre, AB DE toplamı kaç cm teğet, [OK] [PE], PC = 2 cm PA = 2 5 cm, dir? OK = 3 cm olduğuna göre, çemberin yarıçapı kaç cm dir? Örnek 104 Örnek 101 A Çemberde ABC üçgen [AE] açıortay O A AB 3 cm 4 3 AC 4 cm B D B Şekildeki [AB] çaplı yarım çemberin çapı 2 cm ve di- 2 C DC 2 cm E ğer iki yarım çember birbirine eş olduğuna göre, bu Yukarıdaki verilere göre, AE kaç cm dir? üç çembere de teğet olan O merkezli çemberin yarıçapı kaç cm dir? 25 25 DAİREDE ALAN Örnek 105 Örnek 107 D B M A O E C Şekilde, [BC] [DE] Şekildeki gibi, dıştan M ve O merkezli birbirine teğet olan eş çemberler A çemberlerin yarıçapları noktasında teğettir. 2’şer cm ise bu Küçük çember büyük çemberleri saran ipin çember üzerinde o uzunluğu kaç cm dir? yönünde kaymadan yuvarlanmaktadır. B noktası D ile yarım tur döndükten sonra çakıştığına BM göre, oranı kaçtır? MC Örnek 108 K merkezli çember ile Örnek 106 K B A noktasında içten B O A [AB] çaplı çember T T P 2 teğet AB 10 cm G O1 O2 C PB 2 cm E Yukarıdaki verilere göre, küçük çemberin yarıçapı D kaç cm dir? Şekilde [AB] ve [ED] çemberlere teğet, O1 merkezli çemberin yarıçapı 3 birim, O2 merkezli çemberin yarıçapı 15 birim, O1O2= 24 birim olduğuna göre, BCD AGE yay uzunlukları toplamı kaç birimdir? 26 26 DAİREDE ALAN Örnek 109 Örnek 112 [AB] çaplı dairede O merkezli daireyi C noktasında kesen B F E C D FC AB ED AB OABC karesi çizilmiştir. Karenin O C AB 12 cm alanı 25 cm2 dir. A B A FC ED 3 cm ise taralı bölgenin alanı kaç cm2 dir? Yukarıdaki verilere göre, dairenin alanı kaç cm2 dir? Örnek 110 A C Bir kenarı 2 cm olan ABC eşkenar üçgeninin içerisine eş daire dilimler konulmuştur. B Yukarıdaki verilere göre, taralı alan kaç cm2 dir? Örnek 113 O merkezli çemberlerde O Örnek 111 A C O 2 6 L çemberde 2 6 B D AC 2 cm BD 8 cm 2 4 O merkezli çeyrek K C AB 4 cm 8 KL OB Yukarıdaki verilere göre, taralı bölgenin alanı kaç OL LB 2 6 cm cm2 dir? B Yukarıdaki verilere göre, taralı alan kaç cm2 dir? 27 27 DAİREDE ALAN Örnek 114 Örnek 116 B O1 O2 A D A 12 B 18 C O1 ve O2 merkezli eş iki çember verilmiştir. [AB] ortak teğet, AB = 12 cm olduğuna göre, taralı alan kaç cm2 dir? ( = 3 alınız.) D merkezli çemberde B ve C teğetlerin değme noktaları, m(DCB) = 30, AC = 18 cm olduğuna göre, dairenin alanı kaç cm2 dir? Örnek 115 C [AB] çaplı yarım Örnek 117 daireye [BC], B D noktasında teğettir. Yandaki şekil A, D, C doğrusal birbirine eş ve teğet olan, alanı 2 cm2 lik 7 AD DC 2 cm ise daireden taralı bölgelerin A B oluşmaktadır. alanları toplamı kaç cm2 dir? Dıştaki dairelerin ikişer ikişer merkezleri birleştirildiğine göre, taralı bölgenin alanı kaç cm2 dir? 28 28 DAİREDE ALAN Örnek 118 Örnek 120 D O merkezli iki çemberde T noktası A 6 C B ACE daire E S2 teğettir. [BC] dıştaki 3 3 O ABCD kare ve B, S1 içteki çembere T C çemberin çapıdır. diliminin merkezi AB = 6 cm S2 = 2S1 AB AC A AB 6 cm S1 ve S2 B bulundukları TC 3 3 cm bölgenin alanları Yukarıdaki verilere göre, m(ABE) kaç derecedir? Yukarıdaki verilere göre, taralı alan kaç cm2 dir? ( = 3 alınız.) Örnek 119 Örnek 121 [AB] ve [AC] O A A merkezli yarım O merkezli çeyrek dairenin yarıçapı 6 5 cm K çembere E ve D E C noktalarında teğet ve D çemberin yarıçapı 6 B O C m(AKC) m(CMB) E M cm dir. BA AC O AB AC F AE EO OF FB B Yukarıdaki verilere göre, taralı alan kaç cm2 dir? Yukarıdaki verilere göre, taralı alan kaç cm2 dir? 29 29