PowerPoint Sunusu

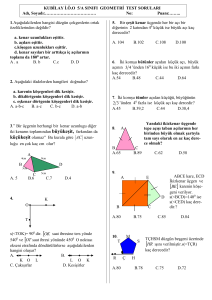
BU BÖLÜMÜN AMAÇLARI

Bu bölümü çalıştığınızda ;
* Çokgenleri tanımlayacak,
* Çokgenlerin temel özeliklerini kavrayacak,
* Çokgenlerde açı kavramını ve çokgenlerin
kenarları arasındaki ilişkileri anlayacak,
* Dörtgen çeşitlerini öğreneceksiniz.

Bu bölümü çalışmadan önce
aşağıdaki konuları öğrenmelisiniz :
- Açı Kavramı
- Üçgende Açılar
- Üçgende Kenarortay Bağıntılar
- Üçgende Açıortay Bağıntılar
- Üçgenlerin Eşliği ve Benzerliği
herhangi üçü doğrusal
olmayan n tane noktayı ikişer ikişer
birleştiren doğru parçalarının
oluşturduğu kapalı şekillere çokgen
denir.
 ÇOKGEN:Düzlemde
 Çokgenler kenar sayılarına göre isimlendirilir. Kenar sayısı 4 olan,
dörtgen; kenar sayısı 5 olan, beşgen; kenar sayısı 6 olan, altıgendir.
 Bir çokgenin içinde alınan herhangi iki noktayı birleştiren doğru
parçasının tamamı çokgenin içinde kalıyorsa çokgene dışbükey (konveks),
doğru parçasının bir kısmı çokgenin dışında kalıyorsa içbükey (konkav)
denir.
 Çokgenin
iç bölgesindeki
açılara, çokgenin iç açıları,
dış bölgesindeki açılara
çokgenin dış açıları denir.
 Bir
çokgenin ardışık
olmayan iki köşesini
birleştiren doğru parçalarına
çokgenin köşegenleri denir.
[AD] doğru parçası bu
çokgenin bir köşegenidir.
Çokgenlerin Özellikleri
 Bir
çokgenin n tane kenarı var ise iç
açılarının toplamı
(n - 2) . 180°
 Üçgen için (3 – 2) . 180° = 180°
 Dörtgen için (4 – 2) . 180° = 360°
 Beşgen için (5 – 2) . 180° = 540°
 Bütün
çokgenlerde, dış açılar toplamı = 360°
 n kenarlı dışbükey bir çokgenin
 Bir köşeden (n – 3) tane köşegen
çizilebilir.
 n kenarlı dışbükey bir çokgenin içerisinde,
bir köşeden köşegenler çizilerek (n – 2)
adet üçgen elde edilebilir.
n
kenarlı bir çokgenin belirtilebilmesi için en az
n-2 tanesinin uzunluk ve n-1 tanesinin açı
olması koşulu ile 2n-3 tane elmanın verilmesi
gerekir.
 Bütün
Düzgün Çokgenler
kenarlarının uzunlukları ve bütün
açılarının ölçüleri eşit olan çokgenlere
düzgün çokgen denir.
Düzgün çokgenin iç açılarının ölçüleri birbirine eşittir.
 Düzgün çokgenin dış açılarının ölçüleri birbirine eşittir.
 n kenarlı bir düzgün çokgende,

ÇOKGEN ÇEŞİTLERİ
DÖRTGEN
YAMUK
EŞKENAR
DÖRTGEN
PARALELKENAR
DELTOİD
DİKDÖRTGEN
KARE
DÖRTGEN
 Bir
düzlemde, herhangi ucu
doğrusal olmayan A, B, C, D
noktaları verilsin. [AB], [BC],
[CD], [DA] doğru
parçalarının birleşim
kümesine ABCD dörtgeni
denir.
DÖRTGENİN ÖZELLİKLERİ

Bir konveks dörtgenin iç
açılarının ölçülerinin toplamı ve
dış açılarının ölçüleri toplamı
360°dir.
 Kenar
uzunlukları a, b, c, d olan,
köşegenleri dik olarak kesişen bir
konveks dörtgenin kenarları
arasında
a2+c2=b2+d2 bağıntısı vardır.
 Köşegenlerin
oluşturduğu karışlıklı
alanların çarpımları eşittir.
S1 . S3 = S2 . S4 dir.
Yalnız iki kenarı paralel olan
dörtgene, yamuk denir.
YAMUK ÇEŞİTLERİ:  Yamuğun paralel olan
İKİZKENAR YAMUK
kenarlarına, yamuğun
tabanları, paralel olmayan
DİK YAMUK
kenarlarına yanal kenarlar
denir.
YAMUK

YAMUĞUN ÖZELLİKLERİ
 Yamuğun, yanal kenarları
üzerindeki açılar bütünlerdir.
 Yan
kenarların orta noktalarını birleştiren doğru
parçasına, orta taban denir. Orta taban
uzunluğu, alt ve üst tabanlarının uzunluklarının
toplamının yarısı kadardır.
 Yamuğun
köşegenleri, orta tabanı K ve L
noktalarında kesmiş olsun. Bu durumda,
İKİZKENAR
YAMUK
 Paralel
olmayan kenarları
eşit olan yamuğa
ikizkenar yamuk denir.
İKİZKENAR YAMUĞUN ÖZELLİKLER
İkizkenar yamukta taban
açılar eşittir.
 Karşılıklı açıların ölçüleri
toplamı 180°dir.


İkizkenar yamukta köşegen
uzunlukları birbirine eşittir.
|AC| = |BD|
DİK YAMUK
 Yanal
kenarlarından biri
dik olan yamuğa, dik
yamuk denir.
DİK YAMUĞUN ÖZELLİKLERİ
 Dik yamuğun yüksekliği dik
kenara eşittir. Yani h = ddir.
 Köşegenleri, dik olarak
kesişen dik yamukta, h2 = a.c
bağıntısı vardır.
PARALELKENAR
 Karşılıklı
kenarları paralel olan dörtgene,
paralelkenar denir.
PARALELKENARIN ÖZELLİKLERİ
 Paralelkenarın karşılıklı açıları eşittir.
 Paralelkenarın ardışık iki açısının açıortayları
dik olarak kesişirler.
 Paralelkenarların
kenarları ve köşegenleri
arasında |BD| = e, |AC| = f ise
e2 + f2 = 2 . (a2 + b2) bağıntısı vardır.
EŞKENAR DÖRTGEN
 Dört
kenarı bir birbirine eşit olan paralelkenara
eşkenar dörtgen denir.
EŞKENAR DÖRTGENİN ÖZELLİKLERİ
 Eşkenar dörtgen, paralelkenarın
bütün özelliklerini taşır.
 Köşegenler
birbirlerini
ortalayarak keserler.
[AC]⊥[BD]
|AK| = |KC| ve |KB| = |KD| dir.
 Kenar
uzunluğu a, köşegenleri
e ve f olan eşkenar dörtgende
e2 + f2 = 4.a2 bağıntısı vardır.
 Köşegenler
açıortaydır ve dik
olarak kesişirler.
DELTOİD
 Tabanları
ortak, ikiz kenar
uzunlukları farklı olan iki tane
ikizkenar üçgenin oluşturduğu
dörtgene deltoid denir.
DELTOİDİN ÖZELLİKLERİ
 İkiz olmayan kenarlar arasında
kalan açılar eşittir.
 [BD] köşegeni B ile D açılarının
açıortayıdır.
 Deltoid’de köşegenler dik
olarak kesişirler.
DİKDÖRTGEN
 Karşılıklı
kenarları
birbirine eşit, dik ve
paralel olan dörtgenlere
dikdörtgen denir.
DİKDÖRTGENİN ÖZELLİKLERİ
 Dikdörtgen,
paralelkenarın
bir özel durumudur.
Dolayısıyla paralelkenarın
tüm özelliklerini taşır.
 Dikdörtgenlerin köşegenleri
eşittir.Birbirlerini
ortalayarak keserler.
P
noktası, dikdörtgenin iç
bölgesinde olmak üzere;
|AP|2 + |CP|2 = |PB|2 + |DP|2 dir.
 P noktası dikdörtgenin dış
bölgesinde olmak üzere;
|AP|2 + |CP|2 = |BP|2 + |DP|2 dir.
KARE
 Bütün
kenarları ve açıları
(90'ar derece) birbirine
eşit olan dörtgendir.
KARENİN ÖZELLİKLERİ
 Kare, paralelkenar ve
dikdörtgenin tüm özeliklerini
taşır. (Bütün kenarları eşit
olduğu için eşkenar
dörtgenin de özelliklerini
taşır.)
 Köşegenler
birbirlerini ortalayarak
ve dik olarak keserler.
|DK| = |KB| = |AK| = |KC| dır.
 Karede
 Karenin
köşegenler açıortaydır.
bir köşegeninin uzunluğu
kenar cinsinden;
ÖZET
KAZANIMLAR



1. Düzgün çokgenlerin kenar ve
açı özelliklerini açıklar.
• Yalnızca dışbükey çokgenler
incelenir.
2. Çokgenlerin köşegenlerini, iç
ve dış açılarını belirler; iç
açılarının ve dış açılarının
ölçüleri toplamını hesaplar.
• İç açılar toplamını keşfetmeye
yönelik çalışmalara yer verilir.
3. Dikdörtgen, paralelkenar,
yamuk ve eşkenar dörtgeni tanır;
açı özelliklerini belirler.
• Kenarların oluşturduğu
açılarla birlikte eşkenar dörtgen,
kare ve dikdörtgende
köşegenlerin oluşturduğu açılar
da incelenir.
• Kare dikdörtgenin ve eşkenar
dörtgenin özel bir durumu olarak
ele alınır. Bunun yanı sıra
dikdörtgen ve eşkenar dörtgen,
paralelkenarın özel halleri olarak
ele alınır. Ayrıca dikdörtgen,
eşkenar dörtgen ve paralelkenar
da yamuğun özel durumları
olarak ele alınır.
KAYNAKÇA
 http://www.meb.gov.tr/aok/aok_kitaplar/AolKitap
lar/Geometri_5/1.pdf
BURAK
GÖLTAŞ
110403075
2-A GÜNDÜZ