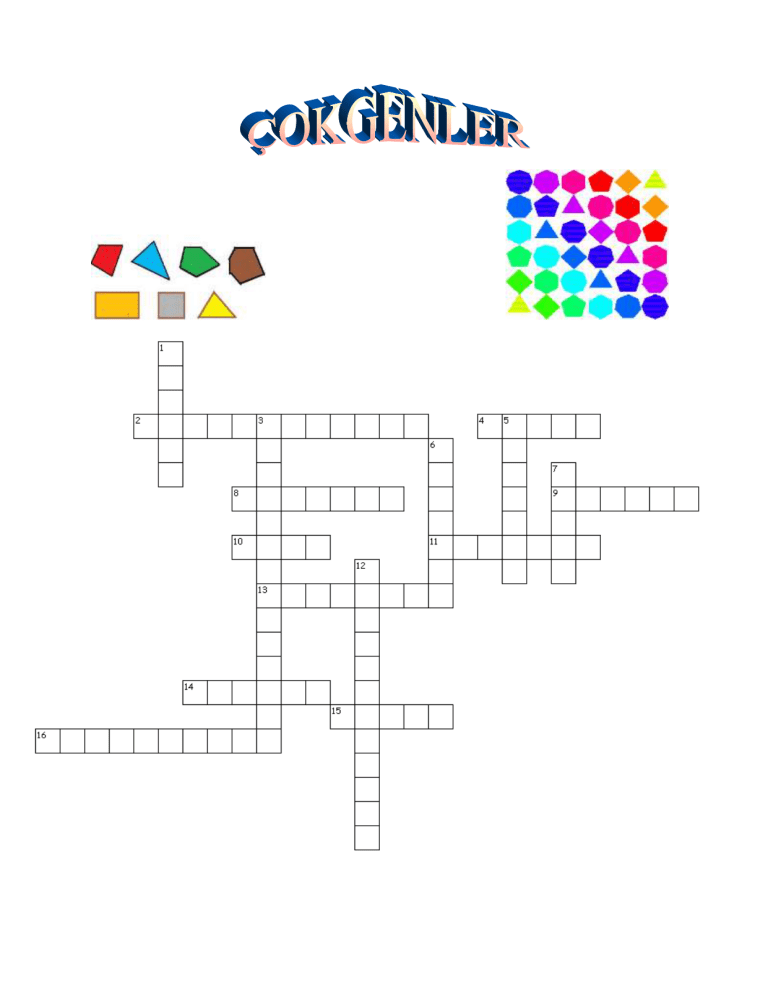
SAĞDAN SOLA
2. Karşılıklı kenarları eşit ve paralel olan iç açıları toplamı 360 derece olan
dörtgenlere denir.
4. Yalnızca iki kenarı paralel olan dörtgenlere denir.
8. Tabanları ortak ikizkenar uzunlukları farklı olan iki tane ikizkenar üçgenin
oluşturduğu dörtgene denir.
9. Düzlemde herhangi üçü doğrusal olmayan n tane noktayı ikişer ikişer
birleştiren doğru parçalarının oluşturduğu kapalı şekillerdir.
10. Bütün kenarları ve açıları (90'ar derece) birbirine eşit olan dörtgendir.
11. Bir çokgenin ardışık olmayan iki köşesini birleştiren doğruya denir.
13. Kenar doğrularının hiçbiri, çokgeni kesmiyorsa bu çokgenlere denir,
konkav
14. Beş kenarı olan çokgendir. İç açıları toplamı 540°, dış açıların toplamı
ise 360°'dir.
15. Çokgenin içine bakan açıdır.
16. Karşılıklı kenarları birbirine eşit, dik ve paralel olan dörtgene denir.
YUKARIDAN AŞAĞIYA
1. Çokgenin dışına bakan açıdır.
3. Dört kenarı birbirine eşit olan paralelkenara denir.
5. Altı kenarı ve altı köşesi olan çokgendir.
6. Bir çokgenin bazı kenar doğruları çokgeni kesiyorsa bu tür çokgenlere
denir, konveks
7. Düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru
parçasının birleşimidir.
12. Tüm kenar uzunlukları ve açıları eşit olan çokgenlerdir.
CEVAPLAR
1.
DİS ACİ
2.
PARALELKENAR
3.
ESKENAR DORTGEN
4.
YAMUK
5.
ALTİGEN
6.
İCBUKEY
7.
UCGEN
8.
DELTOİD
9.
COKGEN
10.
KARE
11.
KOSEGEN
12.
DUZGUN COKGEN
13.
DİSBUKEY
14.
BESGEN
15.
İC ACİ
16.
DİKDORTGEN
KAZANIMLAR
1. Düzgün çokgenlerin kenar ve açı özelliklerini açıklar. • Yalnızca
dışbükey çokgenler incelenir.
2. Çokgenlerin köşegenlerini, iç ve dış açılarını belirler; iç açılarının ve
dış açılarının ölçüleri toplamını hesaplar.
• İç açılar toplamını keşfetmeye yönelik çalışmalara yer verili r.
3. Dikdörtgen, paralelkenar, yamuk ve eşkenar dörtgeni tanır; açı
özelliklerini belirler.
• Kenarların oluşturduğu açılarla birlikte eşkenar dörtgen, kare ve
dikdörtgende köşegenlerin oluşturduğu açılar da incelenir.
• Kare dikdörtgenin ve eşkenar dörtgenin özel bir durumu olarak ele alınır.
Bunun yanı sıra dikdörtgen ve eşkenar dörtgen, paralelkenarın özel halleri
olarak ele alınır. Ayrıca dikdörtgen, eşkenar dörtgen ve paralelkenar da
yamuğun özel durumları olarak ele alınır.
4. Eşkenar dörtgen ve yamuğun alan bağıntılarını oluşturur; ilgili
problemleri çözer.
5. Alan ile ilgili problemleri çözer.
• Üçgen, dikdörtgen, paralelkenar, yamuk veya eşkenar dörtgenden oluşan
bileşik şekillerin alanlarını bulmayı gerektiren problemlere yer verilir.
• Dikdörtgenin çevre uzunluğuyla alanını ilişkilendirmeye yönelik
çalışmalara yer verilir. Aynı alana sahip farklı dikdörtgenlerin çevre
uzunlukları ile aynı çevre uzunluğuna sahip farklı dikdörtgenlerin alanları
incelenir.
BURAK GÖLTAŞ
110403075 2-A GÜNDÜZ