VEKTÖRLER VE
VEKTÖREL IŞLEMLER
1
2- Vektörler ve Vektörel İşlemler
2.1 Tanımlar
Skaler büyüklük: Sadece şiddeti bulunan büyüklükler (örn: uzunluk, zaman, kütle,
hacim, enerji, yoğunluk) Bir harf ile sembolize edilebilir. (örn: kütle: m)
Şiddeti : V
Doğrultusu : AB
Yönü : A’dan B’ye doğru
Uygulama noktası : A
Yatayla yaptığı açı : θ
2
2- Vektörler ve Vektörel İşlemler
2.2 Vektörlerin Sınıflandırılması
Püf noktası 2-a: Sınıflandırmada esas vektörün etkime veya temsil durumunun değişmemesidir.
1-Serbest vektör (Free vector): Belirli bir şiddeti, doğrultusu
ve yönü vardır ama etkime doğrultusu uzayda tek bir noktadan
geçmez. Sabit bir hızla doğrusal hareket yapan bir aracın hız
vektörü buna bir örnektir.
2- Kayan vektör (Sliding vector): Belirli bir şiddeti, doğrultu ve yönü
vardır. Uygulama noktası etkime doğrultusu üzerinde herhangi bir
nokta olabilir. Rijit bir cisme etki eden kuvvet, aynı etkiyi etkime
çizgisi üzerinde herhangi bir noktadan uygulandığında da gösterir ki bu
kuvvet kayan vektöre bir örnektir.
3- Sabit vektör (Fixed vector): Belirli bir şiddeti, doğrultu ve
yönü vardır. Etkime doğrultusu uzayda tek bir noktadan geçer.
Elastik bir çubuğa uygulanan çekme kuvvetleri buna bir misaldir.
Kuvvetlerin aynı etkiyi koruması için etkime doğrultusu ve noktası
sabit olmalıdır.
3
2- Vektörler ve Vektörel İşlemler
2.3 Kaydırılabilme İlkesi (Principle of transmissibility): Rijit cisim üzerine etkiyen
kuvvetin şiddeti, doğrultusu ve yönü aynı kalmak koşuluyla uygulama noktası
doğrultusu üzerinde herhangi bir noktaya taşınabilir ve bu işlem sonucu cisme etkisi
değişmez.
4
2- Vektörler ve Vektörel İşlemler
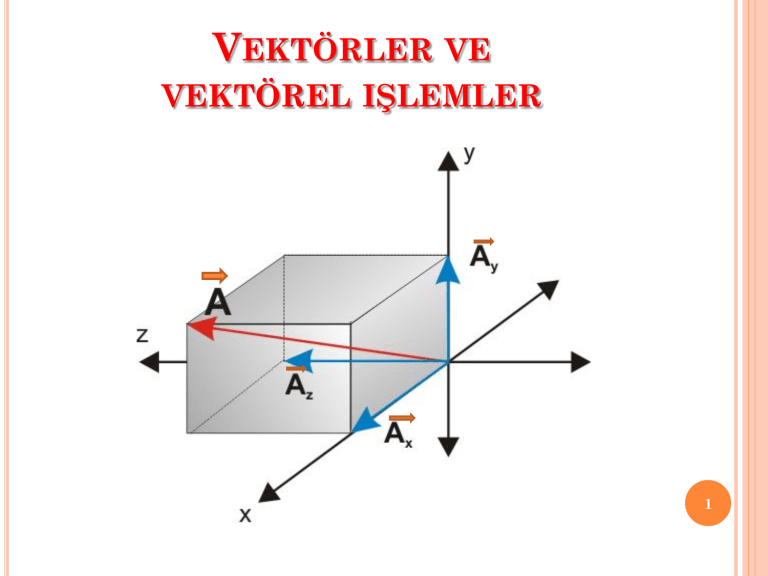
2.4 Kartezyen Koordinatlar : Birbirine dik (ortogonal) eksenlerden oluşan eksen
takımıdır. İki boyutlu (düzlemsel) durumda x ve y eksenlerini, üç boyutlu (uzaysal)
durumda x, y ve z eksenlerini içerir. x-y eksenleri genelde sayfa düzlemi içinde alınır,
yönleri keyfi olarak belirlenebilir; z ekseninin artı yönü ise sağ el kuralına göre belirlenir.
Vidanın dönüş yönü
Sağ vida
5
Vidanın ilerleme yönü
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.1 Toplama - Çıkarma
Vektörlerin Toplama ve çıkarma işleminde 2 yöntem vardır:
a- Paralelkenar kuralı:
Toplama:
Çıkarma:
b- Üçgen Kuralı:
Toplama:
Çıkarma:
6
2- Vektörler ve Vektörel İşlemler
2.5. Vektörel İşlemler
2.5.1 Toplama - Çıkarma
Birden Fazla vektörün toplanması: Üçgen kuralı daha pratiktir.
Vektörler uç uca eklenir ve ilk vektörün başlangıcından son
vektörün ucuna çizilen vektör bileşkeyi verir. Vektörlerin sırasının
önemi yoktur. Çıkarılacak vektörün ise yönü ters çevrilerek eklenir.
7
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.2 Çarpma
a- Bir vektörün bir skalerle çarpımı:
Çarpılan vektörle aynı doğrultuda bir vektördür. Eğer çarpım
katsayısı pozitif ise yönde aynıdır. Sonuçta vektörün şiddeti ile
skaler çarpılır.
8
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.2 Çarpma
b- İki Vektörün Skaler Çarpımı:
İki vektörün skaler çarpımı bir skalerdir. Her iki vektörün
şiddetleri ve aralarındaki açının cosinüsünün çarpılmasıyla
bulunur. Skaler çarpımda « nokta » kullanılır.
9
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.2 Çarpma
c- İki Vektörün Vektörel Çarpım:
Sonuç bir vektördür. Çıkan vektörün şiddeti her iki vektörün şiddetleri ve
aralarındaki açının sinüsünün çarpılmasıyla bulunur. Yönü ise çarpılan
vektörlerin bulunduğu ortak düzleme diktir ve sağ el kaidesiyle bulunurç Vektörel
çarpımda « x » veya «^» kullanılır.
10
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.2 Çarpma
d- Sağ el kaidesi: İlk çarpılan vektörü (A) 2nci vektörün (B) üzerine sağ elimizle dört
parmağımızla kapatırız. Başparmağımızın yönü sonuç vektörünün (C) yönünü verir. Bu yön
çarpılan vektörlerin düzlemine dik yöndür. Bu nedenle vektörlerin çarpım sırası önemlidir.
Vektörel Çapımda Dağılma Özelliği
11
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
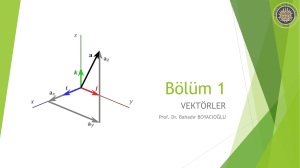
Kartezyen koordinatlarda eksenler
(x,y,z) doğrultularındaki birim
vektörler, özel olarak i, j,k ile
sembolize edilir.
(I)
Buna göre, bir vektör şiddeti ile kendi
doğrultusundaki birim vektörün çarpına
eşittir.
Yani:
(II)
Bir doğrultudaki birim vektörü bulmak için (I) formülü,
Özellikle kartezyen koordinatlarda Vektörün ifadesi için ise (II)
formülü kullanılır. Örnek:
12
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler /Birim Vektör
2.5.3.1 Kartezyen birim vektörlerin vektörel çarpımı:
Aralarındaki açı 90 olan i, j ve k birim vektörlerinin vektörel çarpımı
Şema yardımı ile birim vektörlerin vektörel çarpımı:
i,j,k vektörlerinde herhangi ikisinin çarpımı diğer 3ncü
vektörü verir. İşareti ise yandaki şema yardımıyla
bulunur. Çarpılan ilk vektörden, çarpılan ikinci vektöre
gidiş yolu saat ibresi yönünde ise sonuç pozitif, aksi halde
negatiftir.
Örn-1:
Örn-2:
Şemada j den k ya gidiş saat ibresi yönünde
olduğundan çıkan sonuç + i dir.
Şemada i den k ya gidiş saat ibresi tersi
yönündedir. Bu nedenle çıkan sonuç - j dir.
13
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler /Birim Vektör
Birim vektörlerin kendisi ile vektörel çarpımı sıfırdır.
Birim vektörlerin kendisi ile scaler çarpımı 1 dir.
i × i = i i sin 0 = 0
i × j = i j sin 90 = 1
,
j× j = 0 , k ⋅k = 0
, i× j=k ,
j×k = i
j × i = −k , k × j = − i
, k× i = j
, i×k = −j
Birim vektörlerin diğer birim vektörlerle scaler çarpımı 0 dır. Örn:
14
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.4 Vektörel çarpımın matris formatı:
15
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler /Vektörel Çarpımın Matris Formatı
2.5.4.1 Karışık Üçlü Çarpım: Bir kuvvetin bir doğruya göre momenti
alındığında kullanılır.
U = U xi + U y j + U z k
V = Vx i + V y j + Vz k
W = Wx i + W y j + Wz k
i
U ⋅ (V × W ) = U x i + U y j + U z k ⋅ V x
Wx
(
)
j
Vy
Wy
k
Vz
Wz
veya
Ux
U ⋅ (V × W ) = V x
Wx
Uy
Vy
Uz
Vz
Wy
Wz
16
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler
2.5.6 İzdüşüm :
Bir vektörün bir eksen üzerindeki izdüşümü vektörün ucundan o
eksene inilen dik ile bulunur.
2.5.7 Bileşen:
Bir vektörün 2 farklı eksene göre
bileşenlerini bulmak için, vektörün
ucundan herbir eksene paralel çizgiler
çizeriz. Bu çizgilerin eksenleri kestiği
noktalar vektörün bileşenlerini verir.
17
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler / Bileşen
2.5.7.1 Bileşenle İzdüşüm
Arasındaki Fark:
2.5.7.2 Bileşenle İzdüşüm Ne zaman aynı olur?:
Eksenler birbirine dik olduğunda
bileşen ve izdüşümler üst üste çakışır
ve aynı olur. Kartezyen koordinat
eksenleri (x,y,z) birbirlerine diktir.
18
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler / Bileşen
2.5.7.2 Bir Vektörün Bir Doğruya Dik ve Paralel Bileşenleri
Şunları da görebilmek gerekir:
b
: Aynı zamanda b eksenindeki
izdüşümdür.
θ
U
19
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler / Bileşen
2.5.7.3 İki Boyutlu (Düzlemsel) Kartezyen Koordinatlarda Vektör Bileşenleri
2.5.7.4 Üç Boyutlu (Uzay) Kartezyen Koordinatlarda Vektör Bileşenleri
20
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler / Bileşen
2.5.7.5 Bileşen Örnekleri:
Gerçek yaşamdan bir
örnek
Düzlemde kartezyen
koordinatlara göre
bileşenler. Aynı zamanda
izdüşümlerdir.
Uzayda kartezyen
koordanatlara göre
bileşenler. Aynı zamanda
izdüşümlerdir.
Kartezyen
koordinatlara göre
olan bileşenler Dik
Bileşenler olarak da
isimlendirilir.
21
2- Vektörler ve Vektörel İşlemler
2.5 Vektörel İşlemler / Bileşen
2.5.8 Üç boyutlu vektörlerin kartezyen koordinatlarda gösterilmesi:
Şiddeti:
Birim vektör:
22
2- Vektörler ve Vektörel İşlemler
2.6 Konum Vektörü:
Başlangıç ve bitiş noktasının koordinatları belli olan bir vektörün şu
şekilde bulunur.
23
2- Vektörler ve Vektörel İşlemler
2.7 Kartezyen Koordinat eksenlerinin yerleştirilmesi:
Kartezyen koordinatlardan 2 eksen keyfi olarak yerleştirilir. Ancak 3ncü eksen mutlaka
sağ el kaidesiyle yerleştirilmelidir.
Yerleştirilen eksenlerdeki birim vektörler birbirleriyle, sonuç pozitif çıkacak şekilde
(sırada) çarpılır.
Sağ el kaidesine göre ilk çarpılan vektörü 2ncisi üzerine sağ elimizin 4 parmağı ile
kapatırız. Baş parmağımız çarpım sonucunun yönünü verir ki bu da 3ncü eksenin pozitif
yönüdür.
Soru: Şekle göre +y ekseni ne tarafa olmalıdır.
Cevap: +j çıkması için
24
2- Vektörler ve Vektörel İşlemler
2.8 Örnekler
Çözüm:
25
2- Vektörler ve Vektörel İşlemler
2.8 Örnekler
Örnek 2.8.2: Bir V vektörünün başlangıcı kartezyen
koordinat
sisteminin
başlangıç
noktasına
yerleştirildiğinde uç noktası A (60,30,20)
koordinatlarında ise bu vektörün
a) bu koordinat sistemindeki yazılışını,
b) şiddetini,
c) birim vektörünü,
d) koordinat eksenleri ile yaptığı açıları bulunuz.
26
2- Vektörler ve Vektörel İşlemler
2.8 Örnekler
A(0,1,2) , B(2,0,0)
27
2- Vektörler ve Vektörel İşlemler
2.8 Örnekler
A(0,1,2) , B(2,0,0), C(2,1.5,0)
28