Geometri-10
4. Bölüm Üzerine
Buradaki “4. Bölüm” , önerdiğim programın
“Dik Koordinat Sisteminde Vektörler” başlığı
ile sunduğum bölümüdür. Bu bölüme, eldeki
Geometri-10 programında “Koordinat Sistemleri” başlıklı “3. Bölüm” karşılık gelir.
Muharrem Şahin
Bu ispat, belirli bir düzlemde bir koordinat
sistemini istediğimiz gibi konumlandırabileceğimiz
temeline
dayanmaktadır.
Böylece; trigonometriden yardım alma
durumunda
olan
vektör
kavramı,
trigonometriye
yardım
eder
duruma
gelmektedir. Eğer istenirse; öğrenci, hiç
kafası karışmadan, iki kenarının uzunluğu ile
bu kenarlarının belirttiği açısının ölçüsü
bilinen üçgenin üçüncü kenarının uzunluğunu
iç çarpımdan yararlanarak bulabilecektir.
(Kosinüs Teoremi)
Eldeki programın “Koordinat Sistemleri”
bölümünde şu kazanımlar amaçlanmıştır:
1. Dik koordinat sistemini oluşturur ve
verilen
bir
noktanın
koordinatlarını
belirler.
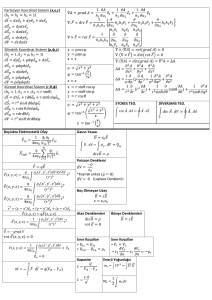
Bu bölümde, bir vektörün kendisi ile iç
çarpımının ne kadar işlevsel olduğu iyice
vurgulanmalıdır. Bu amaçla;
2. İki vektörün Öklit İç Çarpımını açıklar ve
uygulamalar yapar.
3. Bir vektörün uzunluğunu hesaplar.
- Stewart Teoremi,
4. İki vektör arasındaki açının ölçüsünü
hesaplar.
- Kenarortay Teoremi,
- Açıortayın uzunluğunu veren formüller,
5. Bir vektörün başka bir vektör üzerine
dik izdüşümünü belirler ve uygulamalar
yapar.
- Kosinüs teoremi,
- Pisagor Teoremi,
…
Bu kazanımları sağlamak, ilk bakışta
sorunsuz görünür. Ancak; 4. kazanımı
sağlayabilme de sorunlar yaşanır.
gibi teoremler “etkinlik” ya da “örnek
problem” olarak ele alınabilir.
Bu önerilerim programı daha da yüklemek,
daha da ağırlaştırmak olarak görülmemeli.
Eldeki programda bu kavramlar “üçgenler”
konusunda
zaten
işlenmektedir.
Bazı
kavramları, tanım düzeyinde de olsa, “Temel
Kavramlar” bölümünde vermeyi önermem bu
yüzdendir. Yalnız vektör kavramı kullanılarak
bu
teoremlerin
ispatlanması,
vektör
kavramının
işlevsel
olarak
zihinlere
yerleşmesini sağlayacaktır. Bu konudaki
çalışmalarımı ekte veriyorum. Daha önce
gruba yazdığım, bu konularda yararlı
olabilecek
problem çözümlerini de bu
başlığa yeniden göndereceğim.
Benim de katıldığım eleştiriler şöyledir:
İç çarpımın açı türünden ifadesinin ispatı
yoğun Trigonometri bilgisi gerektirmektedir.
Tam yeni bir kavrama girilirken bir başka
kavram
getirilerek
öğrencinin
kafası
karmakarışık edilmektedir.
“Programda iç çarpımın açı türünden ifadesi
ispatsız olarak verilmektedir. Dolayısıyla; bu
kafa karışıklığı yaşatılmayabilir.” denilebilir.
Ama; tanım bir biçimde verilmişken, aynı
kavramla ilgili, tanıma benzer başka bir
bağıntının verilmesi - ezbere yönlendirmesi
yüzünden – doğru olmaz.
Bu sorunun artık olmadığını söyleyebilirim.
Sevgili Arkadaşlarım;
Ekte, iç çarpımın açı türünden ifadesini,
sadece trigonometrik oranların ne olduğunu
bilme düzeyindeki bir trigonometri bilgisi ile
elde edebildiğim dosyayı gönderiyorum.
Ben vektörleri şu anda belli bir düzeyde
kullanabiliyorsam, bunu bu iki bölümü
önerdiğim biçimde çalışmama borçluyum.
“Vektörler” ve “Koordinat sistemleri”
bölümlerini önerdiğim biçimde ele alırsanız,
1
Geometri-10
2. ve 3. Bölüm Üzerine
tüm vektörel sorunlarınızı çözmüş olursunuz.
Tek yapılacak şey, bu iki bölümde geometrik
çözüm yollarının kullanılmamasıdır. Bundan
sonrası gerçekten zevk olur.
Bu önerilerim, kendini vektörlerde iyi
bulmayan
öğretmenlerimedir.
Öğretmenlerim bir kere bu zevki aldıktan
sonra, eldeki kaynakları sınıflarının düzeyine
göre
istedikleri
gibi
kullanabilirler.
Kazandırılacak kavramlara en kolayından en
zoruna kadar olan yelpazede bir sürü örnek
bulunabilir. Sıkışılan durumlarda okulumuza
danışılabilir.
Sevgiler, saygılar.
2
Muharrem Şahin