SIĞA VE
KONDANSATÖRLER
GRUP
SAYISALCILAR
Giriş
Sığa ve Kondansatörler
Bu sunuda sığa kavramını ve kondansatörleri
öğreneceğiz.
Sığa ve Kondansatörlerden LYS sınavında
soru beklenmektedir.
SIĞA VE KONDANSATÖRLER
Sığa
İletkenlerin yük depolamalarının ölçüsü
Kondansatör
Yük depolamaya yarayan devre elemanı
Kondansatörlerin enerjisi
Yük depolamak için harcanan enerji
kondansatörde birikir.
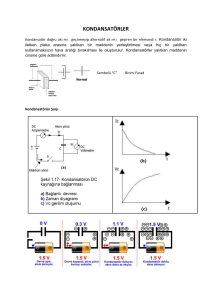
Kondansatörlerin bağlanması
Kondansatörler seri ve paralel bağlanabilir.
SIĞA
Elektrometre
+
+
+
+
+
+ + + + +
İletken
silindir
+
+
+
+
+
+
+q
+q
+q
Yükleme
küreleri
SIĞA
İletken silindirin yükü q
olduğunda elektrometre V
potansiyelini gösterir.
Silindirin yükü 2q
yapıldığında ise
elektrometre 2V
potansiyelini gösterir.
Silindirin yükü 3q ya
çıkarıldığında ise
elektrometre 3V
potansiyelini gösterir.
q 2q 3q
sabit
V 2V 3V
Yükün potansiyeli oranı
sabittir.
Bu sabite iletkenin sığası
denir.
C
q
V
SIĞA
coulomb
Sığa birimi
dir.
saniye
Bunun özel adı Farad’dır.
Farad çok büyük bir birim olduğundan ast katları
kullanılır.
SIĞA
1F 106 F
1nF 109 F
1pF 10
12
F
SIĞA
İletken Bir Kürenin Sığası
Yüklü bir iletken kürenin
potansiyeli
q
V k
r
r
eşitliği ile bulunur.
Bu ifade sığa denkleminde
yerine yazılırsa;
q
q
r
C
C
olur.
V kq
k
r
r
C
k
İletken bir kürenin sığası
sadece yarıçapa bağlıdır.
KONDANSATÖRLER
İki iletken arasına yalıtkan bir ortam
konularak hazırlanan düzeneğe kondansatör
denir.
Kondansatör yük depolamaya yarar.
İletken arasına konulan yalıtkan çoğunlukla;
Boşluk, hava, porselen, cam, mika, kağıt vb.
KONDANSATÖR ÇEŞİTLERİ
Kondansatörler iletken levhaların şekline göre
adlandırılırlar;
İletken levhalar;
düz şeklinde ise düzlem
silindir şeklinde ise silindirik
küre şeklinde ise küresel
kondansatörler olarak adlandırılır.
DÜZLEM KONDANSATÖRLER
d
armatür
armatür
yalıtkan
İletken levhaların her
birine ARMATÜR
denir.
DÜZLEM KONDANSATÖRLER
Bir düzlem kondansatörün sığası
A
C .
d
denklemi ile bulunur.
DÜZLEM KONDANSATÖRLER
ε, yalıtkan ortamın elektrik geçirgenliğidir.
Elektrik geçirgenliği yalıtkan ortamın elektriksel
kuvvetlere karşı gösterdiği direncin bir
ölçüsüdür. Yalıtkan ortamın cinsine bağlıdır.
Boşluğun elektriksel geçirgenliği
o 8,85.10 F / m
12
DÜZLEM KONDANSATÖRLER
Boşluk dışındaki diğer yalıtkan maddelerin
elektriksel geçirgenlikleri
. o
denklemi ile bulunur.
Burada
ya yalıtkan ortamın dielektrik sabiti
denir. Dielektrik sabiti ayırtedici bir özelliktir.
Birimsizdir.
DÜZLEM KONDANSATÖRLER
DÜZLEM KONDANSATÖRLER
Sabit sığalı kondansatörler
Değişken sığalı kondansatörler ise
şeklinde gösterilir.
şeklinde
DÜZLEM KONDANSATÖRLER
Kullanılan levhaların yüzey alanları genellikle
eşittir.
Eğer eşit değil ise küçük levhanın yüzey alanı
dikkate alınır.
KONDANSATÖRÜN ENEJİSİ
Yüksüz bir kondansatörü yüklemek için
levhaların birinden diğerine elektrik yükü
taşımak ve bunun için de iş yapmak gerekir.
Yapılan bu iş kondansatöre enerji olarak
aktarılır.
KONDANSATÖRÜN ENEJİSİ
Buna göre bir kondansatörün enerjisi;
Yük
Yük – potansiyel grafiğinde alan
kondansatörün enerjisini verir.
q
E
1
qV
2
E
1
CV 2
2
Po tan siyel
V
1 q2
E
2C
KONDANSATÖRLERİN
BAĞLANMASI
Birden fazla kondansatörün yaptığı işi tek
başına yapabilen kondansatörün sığasına
eşdeğer sığa denir.
KONDANSATÖRLERİN
BAĞLANMASI
1. SERİ BAĞLAMA
V1
V2
C1
C2
q2
q1
Seri bağlı kondansatörlerde eşit miktarda yük
birikir.
q1 q2
qtoplam
V V1 V2
V
KONDANSATÖRLERİN
BAĞLANMASI
1. SERİ BAĞLAMA
V
Ceş
qt
V
qt
q1 q2
Ceş C1 C2
1
1
1
Ceş C1 C2
KONDANSATÖRLERİN
BAĞLANMASI
1. SERİ BAĞLAMA
Sığaları
C1
ve C2 olan iki kondansatör seri bağlanmışsa eşdeğer sığa
C1.C2
Ceş
C1 C2
Sığaları eşit n tane kondansatör seri bağlanmışsa eşdeğer sığa
C
Ceş
n
olur.
KONDANSATÖRLERİN
BAĞLANMASI
1. PARALEL BAĞLAMA
V1
C1
q1
V2
C
2 q
2
V
Paralel bağlı kondansatörlerin uçları
arasındaki potansiyel farklar eşittir.
V V1 V2
qtoplam q1 q2
KONDANSATÖRLERİN
BAĞLANMASI
1. PARALEL BAĞLAMA
V
Ceş .V C1.V1 C2 .V2
Ceş
qt
Ceş C1 C2
Paralel bağlı kondansatörlerin uçları arasındaki
potansiyel farklar eşittir.
V
Paralel bağlı kondansatörlerin yükleri sığaları ile
doğru orantılıdır.
Örnek 1
Örnek 2
Örnek 3
Örnek 4
Örnek 5
Örnek 6
Örnek 7
Örnek 8
Örnek 9
Örnek 10