Gauss Yasası
Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan
Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik
alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
anlatılmaya çalışılacaktır. Bunun için ilk olarak elektrik akısının
tanımı yapılacaktır.
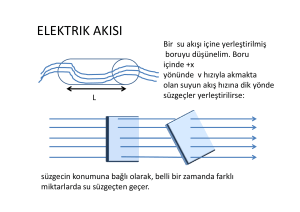
Elektrik Akısı
Şekilde gösterildiği gibi doğrultusu ve büyüklüğü düzgün olan bir
elektrik alanına ait alan çizgilerinin A gibi bir yüzölçümüne sahip bir
dikdörtgen yüzeyden dik olarak geçtiği düşünelim.
Birim yüzeyden geçen alan çizgilerinin sayısının, elektrik alanının
büyüklüğü
ile
orantılı
olduğunu
biliyoruz.
Bu
nedenle,
A
yüzölçümünden geçen alan çizgilerinin sayısı E*A çarpımıyla orantılı
olup elektrik alan büyüklüğü E ile alana dik A yüzölçümünün
çarpımına elektrik akısı (φ-fi-) adı verilmektedir. Matematiksel olarak
bu ifade aşağıdaki tanımlanır.
Bir başka ifadeyle elektrik akısı bir yüzeyden geçen elektrik alan
çizgilerinin sayısı ile orantılı olup birimi Coulomb başına Newton
metrekare (𝑁. 𝑚2 /𝐶) dir.
Örnek Bir Küreden Geçen Akı
Merkezinde +1,00μC’ luk bir yük bulunduran 1,00m yarıçaplı bir
küreden geçen elektrik akısı ne kadardır?
Elektrik alanın geçtiği yüzey alanı alan çizgilerine dik değilse yüzeyden
geçen elektrik akısında bir azalma olacaktır.
Düzgün elektrik alanıyla θ açısı yapan A yüzölçümlü yüzeyin normali
aşağıdaki şekilde gösterilmiştir.
Elektrik alanına dik A’ yüzeyiyle A yüzeyi arasındaki ilişki
𝐴′ = 𝐴 ∗ cos(𝜃) ifadesiyle tanımlanır. Bu durumda A yüzölçümlü
yüzeyden geçen elektrik akısının değeri aşağıdaki ifadeyle hesaplanır.
Bu durumda belli yüzölçümlü bir yüzeyden geçen akı için iki uç durum
söz konusudur.
Birincisi yüzeyin elektrik alanına dik olması durumda (başka bir
değişle, yüzey normalinin elektrik alanına paralel olması durumu θ=0)
akı en büyük değerini alır.
İkinci durumda ise yüzeyin elektrik alanına paralel olması (yani
yüzey normalinin elektrik alanına dik olması θ=90) durumunda ise
akının değeri sıfırdır.
Belirli ve düzgün bir yüzölçümlü yüzeyden geçen akının değeri
∅𝐸 = 𝐸𝐴′ = 𝐸𝐴𝑐𝑜𝑠(𝜃)
ifadesiyle hesaplanabilmektedir. Ancak
düzgün olmayan bir yüzölçümlü yüzeyden geçen akının değerini
hesaplanabilmesi için aşağıdaki şekilde gösterildiği gibi yüzeyin çok
. sayıda ∆𝐴
𝑖
yüzölçümlü küçük yüzey öğelerine bölündüğü
düşünülmektedir.
Bu küçük yüzey öğesinden geçen elektrik akısını belirleyebilmek için
şekilde gösterildiği gibi büyüklüğü i inci yüzey öğesinin yüzölçümünü
göstermek üzere doğrultusu yüzeye dik alınan bir ∆𝑨𝒊 vektörü
tanımlayalım. Bu durumda bu küçük yüzeyden geçen elektrik akısının
değeri ise aşağıdaki gibi tanımlanmaktadır.
Bir 𝐴 vektörü ile bir 𝐵 vektörünün skaler çarpımı 𝐴 ∙ 𝐵 = 𝐴𝐵𝑐𝑜𝑠(𝜃)
olduğundan denklemdeki 𝐸𝑖 ∆𝐴𝑖 cos(𝜃) ifadesi;
şeklinde yazılabilmektedir.
Bütün cisimden geçen toplam elektrik akısı, bütün öğelerin katkısı
toplanarak belirlenebilmektedir. Yüzey öğelerinin yüzölçümleri sıfıra
yaklaştığında sayıları sonsuza ulaşacağında, toplam yerine integral
alınabilir. Bu göre elektrik akısının genel tanımı aşağıda yazıldığı gibidir.
Bu eşitlik söz konusu yüzey üzerinden alınması gereken bir yüzey
integralidir. Dolasıyla elektrik akısının değeri (ϕ𝐸 ) hem elektrik
alanının desenine (𝑬) hem de ilgilenilen yüzey (𝑑𝑨) bağlıdır.
Çoğu elektrik akısı hesaplamalarında kapalı bir yüzeyden geçen
akıyla ilgilenilir. Kapalı yüzeyden kasıt üç boyutlu uzayı iç ve dış
bölgelere ayıran bir yüzey olarak tanımlanır.
Örneğin küre yüzeyi kapalı bir yüzeydir.
Aşağıdaki şekilde gösterildiği gibi kapalı bir yüzey göz önüne alalım.
Şekilde görüldüğü gibi farklı yüzey öğelerinin ∆𝑨𝒊 vektörleri çeşitli
doğrultulara yönelmişlerdir. Her noktada bu vektörlerin yüzeye dik
olduğu ve dışarı doğru yöneldiğini düşünelim. Buna göre birinci
durumda; Elektrik alanı (𝑬) dışarı doğrudur ve 𝜃 < 90° dir. Bu
durumda bu yüzey öğesinden geçen elektrik akısı ∆ϕ𝐸 = 𝑬 ∙ ∆𝑨
pozitiftir.
İkinci durumda; Elektrik alan çizgileri yüzeye tam paralel olup
(yani ∆𝐴𝑖 vektörüne dik) 𝜃 = 90° dir ve durumda bu yüzey
öğesinden geçen elektrik akısı sıfırdır.
Son olarak üçüncü durumda; Elektrik alan çizgileri söz konusu yüzeyi
dışarıdan içeri doğru geçmekte olup açı değeri 180° > 𝜃 > 90°
aralığındadır. Bu durumda bu yüze öğesinden geçen elektrik akısı
∆ϕ𝐸 = 𝑬 ∙ ∆𝑨 negatiftir.
Bütün cisim yüzeyinden geçen net akı, yüzeyden ayrılan alan çizgileri
ile yüzeye giren alan çizgilerinin net sayısıyla orantılıdır denir. Burada
net sayı, yüzeyden çıkanların sayısından, girenlerin sayısının
çıkarılması elde edilir.
Eğer yüzeye girenlerden çok çıkan alan çizgileri varsa, net akı pozitiftir.
Tam tersi çıkandan daha çok alan çizgisi yüzeye giriyorsa net akı
negatiftir. Sonuç olarak; , kapalı bir yüzey üzerinden alınan integrali
göstermek üzere, kapalı bir yüzeyden geçen ϕ𝐸 net akısı,
şeklinde yazılabilir. Burada 𝐸𝑛 , elektrik alanının yüzeye dik olan
bileşenidir.
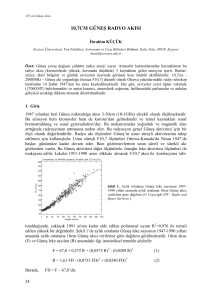
Örnek Bir Küpten Geçen Akı
𝑥 doğrultusunda yönelmiş düzgün bir E elektrik alanı göz önüne
alınsın. Şekildeki gibi 𝑙 kenar uzunluklu bir küpün yüzeyinden geçen
net elektrik akısını bulunuz.
GAUSS KANUNU
Bu bölümde kapalı bir yüzeyden (Gauss yüzeyi) geçen net elektrik
akısıyla, yüzey tarafından sarılan yük arasındaki genel bağıntının
varlığı anlatılmaya çalışılacaktır.
Aşağıdaki şekilde 𝑟 yarıçaplı bir küre ve bu kürenin merkezinde ise
artı bir noktasal yük bulunmaktadır.
Bu kürenin her yüzeyindeki elektrik alanın büyüklüğü 𝐸 = 𝑘𝑒 𝑞/𝑟 2 dir.
Elektrik alan çizgileri ise yarıçap doğrultusunda olup yüzeye her
noktada diktir. Dolayısıyla elektrik alanını 𝑬 her yüzey noktasında o
noktayı saran ∆𝑨𝒊 yüzölçümlü yüzey öğesini temsil eden ∆𝐴𝑖
vektörüne paraleldir. Bu nedenle skaler çarpım eşitliği aşağıdaki gibi
yazılabilir.
Gauss yüzeyinden geçen net akının değeri ise;
ifadesiyle
tanımlanabilir.
Burada
elektrik
alanı 𝐸 = 𝑘𝑒 𝑞/𝑟 2
eşitliğinden dolayı sabittir ve integral dışına alınmıştır. Yüzey ise
küresel olduğundan
𝑑𝐴 = 𝐴 = 4𝜋𝑟 2
yüzeyinden geçen net akı;
dir. Bu nedenle gauss
Burada 𝑘𝑒 Coulomb sabiti olup ifadesi;
olduğundan gauss yüzeyinden geçen net akı;
biçiminde yazılabilir. (𝜖0 boş uzayın elektriksel geçirgenliği)
Bu eşitliğe göre küresel yüzeyden
geçen net akı için aşağıdaki
yorumlar yapılabilir.
1. Küresel yüzeyden geçen net akı, yüzey içindeki yükle orantılıdır.
2. Elektrik alanı 1/𝑟 2 ile, küre yüzeyinin alanı 𝑟 2 ile orantılı
olduğundan, akı 𝑟 yarıçapından bağımsızdır.
3. Şekilde bir 𝑞 yükünü saran çeşitli kapalı yüzeyler bulunmaktadır. Bu
kapalı yüzeylerden 𝑆1 düzgün bir kapalı küresel yüzeyken, 𝑆2 ve 𝑆3
yüzeyleri kapalı ancak küresel bir yüzey değildirler. 𝑆1 yüzeyinden
geçen akı 𝑞/𝜖0 değerindedir.
Hatırlanacağı gibi elektrik akısının değeri o yüzeyden geçen elektrik
alan çizgilerinin sayısıyla orantılıdır. Yukarıdaki şekil incelendiğinde, 𝑆1
küresel yüzeyinden geçen elektrik alan çizgilerinin sayısı, 𝑆2 ve 𝑆3
küresel olmayan yüzeylerden geçen elektrik alan çizgilerinin sayısına
eşittir. İşte bu nedenden dolayı, herhangi kapalı bir yüzeyden geçen
net akının, yüzey biçiminden bağımsız olduğu sonucu çıkarılır ve
dolasıyla bir nokta yükünü saran herhangi bir kapalı yüzeyden geçen
net akı 𝑞/𝜖0 dır denir.
4. Şekilde rastgele biçimli kapalı bir yüzey dışında bulunan bir
noktasal yükü göz önüne alalım. Şekilde görüldüğü gibi bu cisme
giren elektrik alan çizgilerinin sayısı çıkanların sayısına eşittir. Bundan
dolayı yükü sarmayan kapalı bir yüzeyden geçen net elektrik akısı sıfır
denir.
Dolayısıyla hiç hesaplama yapmadan
küp içerisinde yük olmadığından
dolayı küpten geçen net akının değeri
sıfırdır.
Sonuç olarak;
Herhangi kapalı bir yüzeyden geçen net elektrik akısı yalnızca o yüzey
içindeki yüke bağlıdır.
Aşağıdaki şekiller için 𝑆 yüzeyinden geçen elektrik akısı 𝑞1 /𝜖0 iken 𝑆 ′
yüzeyinden geçen elektrik akısı (𝑞2 + 𝑞3 )/𝜖0 dir. 𝑆 ′′ yüzeyi içinde
herhangi bir yük bulunmadığından bu yüzeyden geçen elektrik akısının
değeri sıfırdır.
Bir genelleme yapılarak Gauss yasasına göre, herhangi bir kapalı
yüzeyden geçen net akı;
GAUSS YASASININ KULLANILARAK ELEKTRİK ALANLARININ BELİRLENMESİ
Örnek Bir Noktasal Yükün Elektrik Alanı
Gauss yasasından başlayarak, yalıtılmış bir q nokta yükünün elektrik
alanını hesaplayınız.
Örnek Küresel Simetrili Bir Yük Dağılımı
𝑎 yarıçaplı, dolu bir kürenin düzgün yük yoğunluğu ρ ve toplam
pozitif yükü Q dur.
(a)Kürenin dışındaki bir noktada elektrik alan büyüklüğünü
hesaplayınız.
(b)Kürenin içindeki bir noktada, elektrik alan büyüklüğünü bulunuz.
Örnek 24.8. İnce Küresel Bir Tabakanın Elektrik Alanı
𝑎 yarıçaplı, ince bir tabakanın yüzeyinde düzgün olarak dağılmış toplam Q yükü
bulunmaktadır (Şekil a). Tabakanın içinde ve dışındaki noktalarda elektrik alanını
bulunuz.
Örnek 24.7 Silindirik Simetrili Bir Yük Dağılımı
λ sabit doğrusal yük yoğunluklu, sonsuz uzunlukta, doğrusal artı bir yükten 𝑟 uzaklığında
elektrik alanını bulunuz Şekil (a).
Örnek 24.8 Yalıtkan Düzlem Bir Yük Tabakası
σ (sigma) düzgün yüzey yük yoğunluklu, yalıtkan, sonsuz artı yüklü bir düzlemin elektrik
alanını bulunuz.
Kaynaklar
• Fen ve Mühendislik İçin FİZİK-2
Serway.Beichner Palme Yayıncılık