ortaokul matematik dersi taslak müfredat değerlendirmesi
advertisement

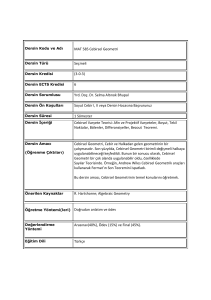
ORTAOKUL MATEMATİK DERSİ TASLAK MÜFREDAT DEĞERLENDİRMESİ Milli Eğitim Bakanlığı’nın yayınlamış olduğu taslak müfredat incelendiğinde genel değişiklikler olmamakla beraber alt kazanımlarda küçük değişikliler yapılmıştır. Genellikle aynı sınıf seviyesinde konuların yerleri değişmiş. Uygulanmakta olan müfredatın mantığı ile devam edildiği açıkça görülüyor. Kazanımları birleştirme arzusu içerisinde olduğu belirgin bir şekilde ortaya çıkmaktadır. Bu durum problem olmamakla birlikte “ Müfredat sadeleştiriliyor, bazı kazanımlar çıkarıldı.” algısı ile birleşince farklı anlamlar içerebilir. Ancak çok dikkat çekici değişiklikler olmamakla beraber sadeleştirmeyi hedefleyen bir değişim gözlenmektedir. Taslak metinde “dinamik geometri yazılımları ile incelemelere yer verilebilir” ifadesi yetersiz kalmaktadır ve dolayısıyla Fatih projesinin ruhu yansıtılmamıştır. 4+4+4 kapsamında çocuklarımızın okula başlama yaşları 66 aya indirilmiştir. Şu an uygulanan müfredat programı da dahil olmak üzere çocuklarımızın yaklaşık 1-1,5 yaş küçük yaşta bu müfredat ile karşılaşacakları dikkate alınılmamıştır. Bu durum çocuklarımızın özellikle soyut kavramları içeren kazanımların sınıf-yaş durumuna uygunluğu kapsamında uygulanabilirliğini ve kalıcılığını azaltacaktır. 8.Sınıf müfredatının uygulanmasında öğretmenlerin karşılaştıkları bazı kafa karışıklıklarına karşın kazanımların daha açıklamalı bir şekilde belirtilmesi kurulun öğretmenlerin geri beslemelerine verdiği tepki anlamında gayet olumlu bir durumdur. Özellikle 8.Sınıf programında öğretmenler arasında bile anlatılıp anlatmaması hususunda çelişki oluşturan ''negatif bilimsel değeri, ebob ekokta alan hacim, çarpanlara ayırma kısmında özdeşliklere bağlı kalınması gibi'' konular açık bir dille sınırlanmış program daha net ve anlaşılır hale getirilmiştir. Taslak metinde “Terimler” ve “Semboller” başlıkları altında eksikliler göze çarpmaktadır. Bazı öğrenme alanları altında terimler veya semboller yeterli iken bazı öğrenme alanlarında hiç verilmemiş veya eksik verilmiştir. Bu durumlar göz önüne alınarak tekrar düzenleme yapılması gerekmektedir. Ramazan TIRNAKSIZ Matematik Öğretmeni Hıdır SAVAŞ Matematik Öğretmeni ( Zümre Başkanı ) Matematik Dersinde Taslak ve uygulanan müfredata göre yapılan değişiklikler ve öneriler şunlardır; 5. Sınıf - M.5.2.2.1. Çokgenleri isimlendirir, oluşturur ve temel elemanlarını tanır. Yalnızca dış bükey çokgenler ele alınır. Ayrıca iç açıların toplamı ve köşegen sayısına değinilmez.Bu kazanımda düzgün çokgenler isim olarak verilebilir. Düzgün beşgen düzgün altıgen gibi... - M.5.2.1.4 kazanımı ( bir doğru parçasına paralel çizme. İki doğrunun paralel olup olmadığını yorumlar) çıkarılmış. - M.5.2.2.3. ve M.5.2.2.4. kazanımlardan(dörtgenleri içerir) Yamuk çıkarılmış. - M.5.2.1.3 ve M.5.3.2.1 kazanımlarından (ağaç şeması) çıkarılmış. Bu kazanım 5.sınıf seviyesine uygundu çıkartılmayabilirdi. 6. Sınıf - Ebob-Ekok konusunda sorular için açıklık getirilmiş gayet güzel olmuş. - M.6.2.1. Cebirsel İfadeler Terimler: cebirsel ifade, değişken, katsayı, terim, sabit terim Bu kazanımda Benzer terim nedir ? ifadesi eklenmeli - M.6.1.3.4. M.6.1.3.5 ve M.6.1.3.5. kazanımlar (Tamsayılarla toplama ve çıkarma işlemlerini içerir) 7. Sınıf müfredatına dahil edilmiştir. - M.7.3.4.1-6 kazanımları(Şekillerin eşliği. Şekillerin öteleme-yansıma ve ardışık öteleme ve yansıma hareketleri altında görüntüleri) 6. Sınıf müfredatına dahil edilmiştir. Bu kazanım 7.Sınıftan itabaren uygulanabilirdi. 7. Sınıf -M.7.1.1.1. Tam sayılarla toplama ve çıkarma işlemlerini yapar; ilgili problemleri çözer. 7. Sınıf müfredatına dahil edilmiştir. Bu kazanım tamsayılarda çarpma ve bölmeden önce verilmesi gerektigi için yerinde bir karar olmuş. - M.7.1.1.3. Tam sayılarla çarpma ve bölme işlemlerini yapar. Bu kazanımda çarpmada sayı pullarının kullanımı öğrencilerin kafasını daha çok karıştırmaktadır. Bunun için basılacak olan kitapta sayı pullarına yer vermemek gerek. - M.7.2.1.2. Denklemi tanır ve verilen gerçek yaşam durumlarına uygun birinci dereceden bir bilinmeyenli denklem kurar.Bu kazanımın altına denklem ile cebirsel ifade arasındaki farkı ayırt eder eklenmeli. - M.7.2.1.2. Denklemi tanır ve verilen gerçek yaşam durumlarına uygun birinci dereceden bir bilinmeyenli denklem kurar.Burada birinci dereceden bir bilinmeyenli denklem diyoruz fakat konu olarak derecenin nereden geldiğini vermiyoruz düşük bir anlatım oluyor. - Ters orantı grafiği verilmeyecektir. - Yüzde kazanımı ile ilgili uyarı kaldırıldığından faiz ile ilgili formüller verilebilir. - Bazı kazanımlar 6. Sınıfa kaydırılıp bazı kazanımlar 6. Sınıftan 7. Sınıf müfredatına eklenmiştir. 8. Sınıf - EBOB-EKOK problemlerinde alan ve hacim problemlerine yer verilmeyecek. - Bilimsel gösterimde kat sayı negatif alınmayacak. Bu kazaımla kafa karışıklığı giderilmiş. - “Tam kare doğal sayılarla bu sayıların karekökleri” ile yer alan ifade “Tam kare pozitif tam sayılarla bu sayıların karekökleri” olarak düzenlenmiş yani 0’ın karesi verilmeyecektir. Bu kazaımla kafa karışıklığı giderilmiş. - Çarpanlarına ayırma kazanımında aşağıdaki uyarılar getirilmiştir. a) Ortak çarpan parantezine alma ile iki kare farkı ve a² ± 2ab + b² biçimindeki tam kare ifadelerin çarpanlara ayırma işlemleri ele alınır. Cebirsel ifadelerdeki katsayılar ve kökleri tam sayılar içinde kalacak biçimde seçilir. b) Gruplandırarak çarpanlarına ayırma yöntemine girilmez. c) Tam kare olmayan ikinci dereceden ifadelerin çarpanlara ayrılma işlemlerine girilmez. Bu kazanımla çarpanlaranı ayırma daha sade hale gtirilmiş. - Benzerlik kazanımında “problemlere girilmez” uyarısı eklenmiştir. Bu kazaımla kafa karışıklığı giderilmiş. - Bir olayın olma ve olamama olasılıkları toplamının 1 yaptığı vurgulanacak. Birden fazla olayın olma olasılığı ele alınmaz uyarısı getirilmiş. Ramazan TIRNAKSIZ Hıdır SAVAŞ Matematik Öğretmeni Matematik Öğretmeni ( Zümre Başkanı )