4.5. Thevenin Teoremi - Kocaeli Üniversitesi

Elektrik Devre Temelleri
7
DEVRE TEOREMLERİ
Doç. Dr. M. Kemal GÜLLÜ
Elektronik ve Haberleşme Mühendisliği
Kocaeli Üniversitesi
4.5. Thevenin Teoremi
• Bir çok devrede, bir eleman hariç diğer elemanların
değerleri sabittir.
• Değişken değerli olan bu devre elemanı “yük” olarak
adlandırılır.
• Örneğin, şebekeye bağladığımız elektrikli süpürge, fırın,
şarj cihazı gibi ekipmanlar şebekeye göre yük olurlar ve
değerleri değişkenlik gösterir.
• Yükün değişimine bağlı olarak her durum için devreyi
tekrar analiz etmek yerine, Thevenin teoremini
kullanarak devrenin değişmeyen kısmının eşdeğer
devresi bulunabilir
• Bu sayede, yükün değişimine bağlı devreden çekeceği
akım kolayca bulunabilir.
4.5. Thevenin Teoremi
• Thevenin teoremine göre doğrusal bir devre, eşdeğer
devre ile aşağıdaki gibi gösterilebilir.
Orijinal devre
Eşdeğer devre
4.5. Thevenin Teoremi
• Thevenin teoreminde iki uçlu doğrusal bir devre, bir 𝑉𝑡ℎ
gerilim kaynağı ve bu kaynağa seri bağlı bir direnç 𝑅𝑡ℎ direnci
ile ifade edilir.
• 𝑽𝒕𝒉 ; a-b uçlarındaki açık devre gerilimi,
𝑹𝒕𝒉 ; direnci ise bağımsız kaynaklar kapatıldığında a-b uçlarındaki eşdeğer
direnci gösterir.
4.5. Thevenin Teoremi
NOT: İki ayrı devrenin çıkış uçları arasındaki gerilim/akım ilişkisi
aynı ise bu iki devre eşdeğerdir denir.
𝑹𝒕𝒉 direncini bulmak için:
• 𝑹𝒕𝒉 direncini bulmak için devrenin iki özel
durumunu dikkate almamız gereklidir.
1. DURUM: Eğer devrede bağımlı kaynak
yok ise, bütün bağımsız kaynaklar kapatılır
ve istenilen a-b çıkışından görülen eşdeğer
direnç hesaplanır.
4.5. Thevenin Teoremi
2. DURUM: Eğer devrede bağımlı kaynak var
ise, bütün bağımsız kaynaklar kapatılır. Bağımlı
kaynaklar devre değişkenleri tarafından kontrol
edildiği için kapatılamazlar. Bu durumda a-b
Direncin
𝑹𝒕𝒉 = 𝑽uygulanarak
𝒐 /𝒊𝒐 ile hesaplanır.kaynaktan
uçlarına
birdeğeri;
𝑉𝑜 gerilimi
geçen 𝑖𝑜 akımı bulunur.
4.5. Thevenin Teoremi
• Alternatif olarak a-b uçlarına 𝑖𝑜 akım
kaynağı da bağlanabilir.
Direncin değeri; 𝑹𝒕𝒉 = 𝑽𝒐 /𝒊𝒐 ile hesaplanır.
• • Bu
durumda iki ucu arasındaki gerilim farkı
Her iki yöntem de aynı 𝑹𝒕𝒉 değerini verir.
𝑉𝑜 hesaplanır.
• NOT: Bazı durumlarda 𝑹𝒕𝒉 direnci negatif çıkabilir. Bu durumda negatif
direnç değeri devrenin güç sağladığı anlamına gelir (𝑣 = −𝑖𝑅).
• Bu aynı zamanda bağımlı kaynak varken mümkün olabilir.
4.5. Thevenin Teoremi
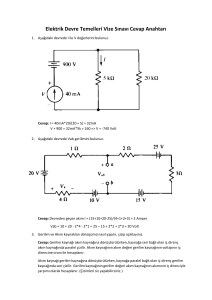
Örnek 4.8
• Thevenin eşdeğeri? R = 6 Ω/16 Ω/36 Ω iken
çıkış akımı?
Örnek 4.8
• Thevenin eşdeğer devresi:
Örnek 4.9
• a-b uçları arasındaki
Thevenin eşdeğerini
bulun.
– RTh’ın bulunması:
Örnek 4.9
– VTh’ın bulunması:
– Thevenin eşdeğeri:
Problem 4.9
4.6. Norton Teoremi
• Bu teoreme göre doğrusal iki uçlu devre, aynı
özelliği gösterebilecek bir 𝐼𝑁 akım kaynağı ve
bu kaynağa paralel bağlı bir 𝑅𝑁 direnci ile
ifade edilebilir.
• 𝑰𝑵 iki uç arası kısa devre akımını,
• 𝑹𝑵 ise bağımsız kaynaklar kapatıldığında iki uç
arasındaki eşdeğer direnci gösterir (𝑅𝑁 =
𝑅𝑡ℎ ).
4.6. Norton Teoremi
• 𝑹𝑵 direnci; Thevenin teoremindeki 𝑅𝑡ℎ
direncini bulmak için izlenen adımların
aynısı uygulanır.
• 𝑰𝑵 akımını bulmak için;
a-b uçları kısa devre akımı hesaplanır
(𝐼𝑁 = 𝐼𝑠𝑐 ).
Bağımlı ve bağımsız kaynaklar Thevenin
teoreminde olduğu gibi değerlendirilir.
4.6. Norton Teoremi
• NOT: Dikkat edilecek olursa, Thevenin ve
Norton teoremleri arasında kaynak
dönüşümü ilişkisi vardır (𝑅𝑁 = 𝑅𝑡ℎ ). Bu
nedenle dönüşüm aynı zaman TheveninNorton dönüşümü olarak da bilinir.
Örnek 4.11
• Norton eşdeğer devresini bulun.
Örnek 4.11
– Norton eşdeğeri:
Örnek 4.12
• Norton eşdeğer devresini bulun.
Problem 4.12