akışkanlar mekaniği - Erzurum Teknik Üniversitesi

Yrd. Doç. Dr. Fatih TOSUNOĞLU
Erzurum Teknik Üniversitesi
Mühendislik Fakültesi
İnşaat Mühendisliği Bölümü
1
Akışkan Statiğine Giriş
Akışkan statiği (hidrostatik, aerostatik),
durgun
haldeki
akışkanlarla
ilgili
problemleri ele alır.
Akışkan Statiğine Giriş
Bir yüzey akışkana daldırıldığı zaman
akışkandan dolayı yüzeye bir kuvvet etkir.
Depoların, gemilerin, barajların ve diğer
hidrolik yapıların dizaynında bu kuvvetlerin
bilinmesine gereksinim vardır.
Düzlem Yüzeye Etkiyen Hidrostatik Kuvvetler
Hareketsiz akışkanlarda, kayma gerilmesi
olmadığı için bu yüzeye dik olduğu bellidir.
Ayrıca, eğer akışkan sıkıştırılamaz ise
basıncın derinlikle lineer (doğrusal) olarak
değiştiği bilinir.
Çoğunlukla düzlemsel yüzeyin bir yüzü
atmosfere
açık
olduğundan
atmosfer
basıncı düzlemsel yüzeyin her iki yüzüne de
etkiyerek sıfır bileşke kuvvet oluşturur. Bu
tür
durumlarda
atmosferik
basıncı
çıkarmak ve sadece etkin basınçla çalışmak
daha uygundur.
Şekil 2.2 Dalmış düz yüzeylere etkiyen kuvvetler.
Sıvı ile dolu tankın (Şekil 2.3a) taban
yüzeyi gibi yatay yüzeyler için, bileşke
kuvvetin büyüklüğü FR  P * A ’dır. Burada
P tankın tabanına etkiyen üniform basınçtır
ve
a
tankın
taban
alanıdır.
Şekilde
gösterilen açık tank için P   * h’dır.
Şekil 2.3 a. Üstü açık bir tankın tabanına etkiyen hidrostatik kuvvet ve basınç dağılımı
b. Üstü açık tankın yan yüzeylerindeki basınç dağılımı
Eğer tankın tabanının her iki yüzeyine de atmosferik
basınç etkiyorsa tankın tabanına etkiyen bileşke
kuvvet sadece tankın içindeki sıvıdan dolayı olur.
Tabana etkiyen basınç sabit ve üniform olarak
dağılmış olduğundan dolayı bileşke kuvvet Şekil
2.3.a da gösterilen alanın merkezine etkir. Şekil 2.3.b
de gösterildiği gibi, tankın yan yüzeylerine etkiyen
basınç üniform değildir. Bu durumda, bileşke kuvvetin
belirlenmesi aşağıda izah edildiği gibi yapılır.
Şekil 2.4 Eğik olarak daldırılmış düzlem yüzeye etkiyen hidrostatik kuvvet
Şekil 2.4’de gösterilen, eğik olarak daldırılmış düzlem
yüzeye etkiyen bileşke kuvveti belirleyelim. Akışkanın
yüzeyinin atmosfere açık olduğunu kabul edelim. Şekil
2.4’de gösterildiği gibi, daldırılmış yüzeyin bulunduğu yüzey
serbest yüzey ile 0 noktasında θ açısı ile kesişsin. 0 orijin
olmak üzere x-y eksen sistemi tanımlansın.
Yüzey şekilde gösterildiği gibi keyfi bir
şekle sahip olsun. Sıvı ile temastan
dolayı bu yüzeyin bir yüzüne etki eden
bileşke kuvvetin yönünü, konumunu ve
büyüklüğünü belirlemeye çalışalım.
Herhangi bir h derinliğinde, dA’ya (Şekil 2.4 diferansiyel
alan) etkiyen kuvvet,
Böylece,
tüm
dF   * h * dA
yüzey
boyunca
olup yüzeye diktir.
diferansiyel
kuvvetler
toplanarak bileşke kuvvetin büyüklüğü bulunabilir. Eşitlik
şeklinde aşağıdaki şekilde
FR    * h * dA    * y *sin  * dA
A
A
ifade edilebilir. Burada h
 y * sin
‘dır. Sabit  ve  icin,
FR   *sin   y * dA
(2.7)
A
elde edilir. Denklem 2.7’de verilen integral, x eksenine göre
alanın birinci momenti olduğu için
 y * dA  yC * A
A
şeklinde yazılabilir. Burada yc , A alanının merkezinin y
koordinatıdır. Böylece denklem 2.7,
FR   * A * yC *sin 
şeklinde yazılabilir veya daha basit olarak
FR   * hC * A
(2.8)
şeklinde ifade edilebilir. Yandaki şekilde
gösterildiği gibi, hc akışkanın serbest yüzeyinden
alanın merkezine olan dikey mesafedir. Kuvvetin
büyüklüğünün, θ açısının bir fonksiyonu olmadığı,
sadece akışkanın özgül ağırlığının, daldırılmış
yüzey alanının ve bu alanın merkezinin
derinliğinin bir fonksiyonu olduğu hususunu
belirtmek gerekir. Bileşke kuvvet FR’ı elde etmek
için yüzeye etkiyen diferansiyel kuvvetler
toplandığı için, bileşke kuvvet FR ‘da daldırılmış
yüzeye dik olacaktır.
Sezgilerimiz bileşke kuvvetin, alanın merkezinden geçeceği
yönünde olmasına rağmen bu sezgi doğru değildir. Bileşke
kuvvetin y koordinatı yR, x ekseni etrafında momentlerin
toplanmasıyla belirlenebilir. Yani, bileşke kuvvetin momenti,
yayılı basınç kuvvetinin momentine eşit olmalıdır.
FR   * A * yC *sin  olduğundan,
yR 
y
2
* dA
A
yc * A
İntegralin pay kısmı, Ix, daldırılmış yüzeyin bulunduğu
yüzey ile serbest yüzeyin arakesiti tarafında oluşan eksene
(x eksene) göre alanın ikinci momentidir (atalet momenti).
Böylece
Ix
yR 
yc * A
yazılabilir. Paralel eksen teoremi kullanılarak Ix
I x  I xc  A * yc 2
şeklinde ifade edilebilir. Burada Ixc, x
eksenine paralel ve alanın merkezinden
geçen eksene göre alanın ikinci momentidir.
Böylece
olur. Denklem 2.9 ve aşağıdaki şekilde gösterildiği gibi,
bileşke kuvvet merkezden geçmez.
I xc
 0 olduğundan
yc * A
o
daima
merkezin
altındaki
bir
noktadan geçer.
Bileşke kuvvetin x koordinatı xR, y eksenine
göre momentler benzer şekilde toplanarak
belirlenebilir:
Burada IxyC, alanın merkezinden geçen ve xy koordinat sisteminin aktarımı ile
oluşturulan dik koordinat sistemine göre
çarpım atalet momentidir.
Eğer daldırılmış alan merkezde geçen bir eksene göre simetrik ise
ve x veya y eksenine paralel ise Ixyc = 0 olduğundan bileşke
kuvvet x = xc doğrusu üzerinde olur. Bileşke kuvvetin etki ettiği
nokta basınç merkezi olarak adlandırılır.
Denklem 2.9 ve 2.10’dan görüldüğü gibi, yc
arttıkça basınç merkezi, alanın merkezine
doğru yaklaşır. yc  hc sin  olduğundan eğer
batma derinliği hc artarsa veya verilen bir
derinlik için daldırılmış yüzey döndürülerek θ
açısı azalırsa yc mesafesi artar. Bu nedenle,
yandaki şekilde gösterilen kapının sağ
yüzeyine etkiyen hidrostatik kuvvet, sol
yüzeyine etkiyen hidrostatik kuvvete göre
alanın merkezine daha yakındır.
Şekil 2.5 Bazı yaygın kullanılan şekillerin geometrik özellikleri
18
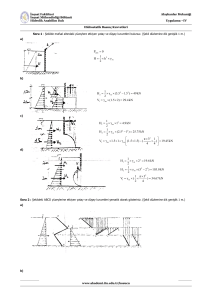
 Örnek : Şekilde verilen 4 m çapındaki dairesel kapı su ile dolu
büyük bir rezervuarın eğik duvarı üzerine yerleştirilmiştir. Kapı
onun yatay çapı boyunca yataklanmış olup yatağın üzerindeki
su derinliği 10 m’dir. Su tarafında kapıya uygulanan bileşke
kuvveti ve eksentrisiteyi bulunuz.
19
 Suyun kuvvetinin büyüklüğünü bulmak için denklem 2.8’i
uygulayabiliriz.
FR   * hC * A
 Serbest yüzeyden alanın merkezine olan dikey mesafe 10 m olduğu
için
FR  (9810 N/m )*(10m)*( *2 m )
3
2
2
20
Eksentrisite = Basınç Merkezi – Ağırlık Merkezi
e = yR - yc
FR’nin etki ettiği basınç merkezinin
konumunu bulmak için denklem 2.9
kullanılırsa
I xc
yR 
 yc
yc * A
I xc 
 * R4
4

 * 24
4
 4* 
4* 
yR 
 10 sin 60 
2
10 sin 60  *( *2 )
yR  0.0866  11.55  11.6366 m
e  yR  yc  11.6366  11.55  0.0866 m
21
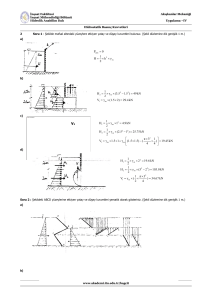
 Örnek : A noktasından mafsallı AB dikdörtgen kapağın genişliği 4
m’ dir. Kapağın açılmaması için B noktasına uygulanması gereken
kuvvetin şiddet ve yönü ne olmalıdır ?
22
 Çözüm 1:
F   .hC . A
yR 
I xc
I xc
 yC
yC * A
b * h3 4* 2, 43


 4, 608 m4
12
12
F1  9810 * (2,1  1, 2) * 4 * 2, 4  310780,8 N
F2  9810 * (1, 2) * 4 * 2, 4  113011, 2 N
yR1 
4, 608
 3,3  3, 445 m
3,3*9, 6
yR 2 
4, 608
 1, 2  1, 6 m
1, 2*9, 6
M F A  310780,8*(3, 445  2,1)  418 kNm
1
M F A  113011, 2 * (1, 6)  180,817 kNm
2
M  0  419,55  180,82  FB *2, 4
FB  98.8 kN
23
 Çözüm 2:
F1  (9810 * 2,1) * 2, 4 * 4  197769, 6 N
M  197769, 6*(2, 4 / 2)  FB *2, 4  0
FB  98, 8 kN
24
 Örnek: Şekildeki A-B kapağı A noktasında mafsallı olup B
noktasına 284490 N luk P kuvveti etkimektedir. Kapağın hareketsiz
k alması için gerekli h yüksekliğini hesaplayınız.
25
Fx   * hC * A  9810*(h  1,5)*(3*8)
Fx  235440*(h  1,5) N
3
I xc
3
b*h
8*3


 18 m 4
12
12
I xc
yR 
 yC
yC * A
18
0, 75
yR 
 (h  1,5) 
 (h  1,5)
(h  1,5)*(3*8)
(h  1,5)
26
 0, 75

235440*(h  1,5) * 
 ( h  1,5)  h   284490*3
 (h  1,5)

 0, 75

235440*(h  1,5) * 
 1,5  853470
 (h  1,5)

 0, 75  (h  1,5)*1,5 
(h  1,5)* 
 3, 625

(h  1,5)


0,75+(h+1,5)*1,5=3,625 
h= 0,42 m
27
2.5.4 Silindirik Yüzeylere Etki Eden Basınç Kuvvetleri
 Bir eğri yüzey düşünelim ve bu eğri yüzey, bir yönde eğriliğe sahip
olsun. Bu yüzeyin şekil düzlemine dik uzunluğu ℓ olsun. Bu yüzeye
etkiyen yatay ve düşey itki bileşenlerini hesaplayalım.
 Bu yüzeyin alanı (ds.ℓ ) olan elemanter parçasına gelen basınç p = p0
+ γ.h dır. Aynı parçaya yüzeyin dış tarafında p0 atmosfer basıncı
etkiyecektir. O halde bileşke basınç γ.h olacaktır. Bu parçaya etkiyen
basınç kuvveti ise dF = γ.h. (ds.ℓ) dir. Bu kuvvetin bileşenleri,
28
dFx   .h.ds. .cos    .h. .dh
dFh   .h.ds. .sin    .h. .dx
 olarak yazılabilir. Bütün alana gelen kuvvetin yatay ve düşey
bileşenleri ise,
H
Fx  .  h.dh 
0
 .H 2
2
H
Fh  .  h.dx  . . Alan(OBAO)
0
 O halde bir eğri yüzeyi üzerine tesir eden herhangi bir yöndeki
yatay basınç kuvvetinin değeri, bu yüzeyin bahis konusu yöne
dik düzlem üzerindeki izdüşümü üzerine tesir eden kuvvete
eşittir.
29
 Örnek : Şekilde gösterilen ABC yüzeyine etki eden hidrostatik
basınç kuvvetini hesaplayınız. Şekle dik derinliği 1 m olarak
alınız.
A
B
2m
6m
C
30
Eğrisel yüzeylere etkili hidrostatik basınç kuvveti iki aşamada
hesaplanacağından
a. Yatay kuvvetin hesabı (Fx)
A
Fx2
Fx
Fx1
C
6
Fx1   .hC . Ax  9,81. .(6.1)  176,58 kN
2
8
Fx 2   .hC . Ax  9,81. .(8.1)  313,92 kN
2
Fx  Fx 2  Fx1  313,92  176,58  137,34 kN
31
b. Düşey kuvvetin hesabı (Fh)
Kapağa sol taraftan gelen düşey kuvvetler
A
B
C
Kapağa sağ taraftan gelen düşey kuvvetler
D
O
A
B
C
32
Düşey bileşke kuvvet
D
A
O
B
Fh
C
Fh   .b. Ay
Ay  ( ABCOD)  (OBC )  (ODAB)
Fh  9,81.1.(2.6)  117, 72 kN
c. Bileşke kuvvet
F  Fx 2  Fh 2  137,342  117,722  180,89 kN
33
 Örnek : Şekildeki AG kapağının 1 m genişliğine gelen yatay ve
düşey hidrostatik kuvvetleri bulunuz.
A
1m
B
C
1,5 m
D
2m
E
F
0,5 m
G
34
Kapağa gelen yatay kuvvet, şekilde görüldüğü gibi soldan ve sağdan
gelen yatay kuvvetlerin bileşkesi olarak aşağıdaki gibi bulunur:
A
B
C
D
Fx1
E
F
Fx2
35
Düşey kuvvet :
Kapağa gelen düşey kuvvet, aşağıda gösterilen düşey kuvvetlerin
bileşkesi olarak bulunur. Şekilde görüldüğü gibi, eşit ve zıt yönlü
düşey kuvvetlerin birbirini götürmesi sonucunda, geriye düşey kuvvet
olarak, çeyrek dairesel hacmi dolduran suyun ağırlığı kalmaktadır,
yani:
Kapağa sol taraftan gelen düşey kuvvetler :
A
A
B
B
C
C
C
D
D
E
F
+
=
E
E
F
C
C
F
E
F
E
F
36
Kapağa sağ taraftan gelen düşey kuvvetler
A
B
C
C
C
D
+
=
E
F
E
E
F
F
37
C
C
C
=
+
E
F
E
E
F
F
38
 Örnek : Şekilde kesiti verilen düşey düzleme dik derinliği 1 m olan
tankın içerisinde su bulunduğuna göre C-D kapağına etki eden
hidrostatik basınç kuvvetinin düşey bileşenini hesaplayınız.
39

 *52 
Fh   .  9810.  4*5 
 .1
4 

Fh =388819 N = 389 kN
40
Rijit Cisim Hareketi Yapan Akışkanlar
Süt ve benzin gibi çoğu akışkan
tankerlerle taşınır. İvmelenen bir
tankerde akışkan geriye hücum eder ve
başlangıçta bazı çalkalanmalar oluşur.
Ancak bunun ardından yeni bir serbest
yüzey meydana gelir.
Rijit Cisim Hareketi Yapan Akışkanlar
Bu esnada her bir akışkan parçacığı aynı ivmeye
sahiptir ve tüm akışkan gövdesi sanki katı bir
cisim gibi hareket eder.
Herhangi bir şekil değiştirme olmadığından
akışkan içerisinde bir kayma gerilmesi
oluşmaz.
Rijit Cisim Hareketi Yapan Akışkanlar
z ekseni düşey ve yukarı doğru olmak üzere x, y
ve z yönlerindeki kenar uzunlukları sırasıyla dx,
dy ve dz olan dikdörtgen şeklindeki diferansiyel
bir akışkan elemanını dikkate alalım.
Rijit Cisim Hareketi Yapan Akışkanlar
Akışkan elemanın rijit cisim hareketi yaptığı düşünülerek bu
eleman için Newton’un ikinci hareket yasası
 F   m*a
 m   * d   * dx * dy * dz
Elemanın merkezindeki basıncı P alarak, üst
ve alt yüzeylerindeki basınçlar P dz
P dz
P
z 2
, P
z 2
olur. F = P*A dan hareketle z yönünde eleman
üzerine etkiyen net kuvvet, alt ve üst
yüzeylere etki eden basınç kuvvetlerinin
farkıdır.
 FS , z
P dz 
P dz 
P


P
dx * dy * dz
 dx * dy   P 
 dx * dy  
z 2 
z 2 
z


Rijit Cisim Hareketi Yapan Akışkanlar
Benzer şekilde x ve y yönlerindeki net kuvvetler,
P
 FS , x   dx * dy * dz
x
P
 FS , y   dx * dy * dz
ve
y
Elemanın tamamına etkiyen yüzey kuvveti
vektörel formda
 FS   FS , x * i   FS , y * j   FS , z * k
 P
P
P 
 FS    i 
j
k  dx * dy * dz  P * dx * dy * dz
y
z 
 x
P
P
P
P 
i
j
k
Basınç gradyeni
x
y
z
Rijit Cisim Hareketi Yapan Akışkanlar
Akışkan elemanı üzerine etkiyen tek kütle kuvveti, negatif z
yönünde etkiyen kendi ağırlığı olup
FB, z   g *  m    * g * dx * dy * dz
veya vektörel formda
 FB, z   g * m * k    * g * dx * dy * dz * k
Akışkan elemanı üzerine etkiyen toplam kuvvet
 F   FS   FB  (P   * g * k )* dx * dy * dz
 F   m * a   * dx * dy * dz * a yerine yazılıp dx * dy * dz sadeleştirilirse
Genel hareket denklemi
P   * g * k    * a
Rijit Cisim Hareketi Yapan Akışkanlar
Vektörler bileşenlerine ayrılırsa
P
P
P
i
j
k   * g * k    (ax i  a y j  a z k )
x
y
z
Kartezyen koordinatlarda skaler formda
P
   * ax
x
P
  * ay
y
P
   *( g  az )
z
Durgun halde veya doğrusal bir yörünge üzerinde sabit hızla
hareket eden akışkanlar için
P
0
x
P
0
y
P
  * g
z
Durgun haldeki akışkanlarda basıncın herhangi bir yatay
doğrultuda sabit kaldığını (P, x ve y’den bağımsız) ve
yerçekiminin bir sonucu olarak yalnızca düşey doğrultuda
değiştiğini doğrulamaktadır.
Rijit Cisim Hareketi Yapan Akışkanlar
Akışkan az sabit ivmesi ile yukarı doğru hareket ederse
ax  a y  0
P P

0
x y
P
   *( g  az )
z
Akışkan az sabit ivmesi ile aşağı doğru hareket ederse
ax  a y  0
P P

0
x y
P
   *( g  az )
z
Rijit Cisim Hareketi Yapan Akışkanlar
Doğrusal yörünge üzerinde ivmelenme
Rijit Cisim Hareketi Yapan Akışkanlar
Doğrusal yörünge üzerinde ivmelenme
ax
tan  
g  az
Tankın yüksekliği = h 0  z
z
tan  
b2
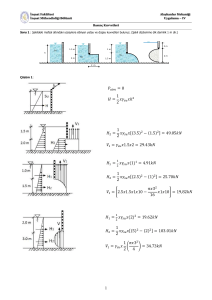
 Örnek 2.11: Şekilde görülen 2x2 tabanlı bir tank 1,5 m
derinliğinde su ile doludur. Aşağıdaki durumlar için tankın tabanına
gelen kuvvetleri bulunuz.
52
ax
3
tan  

 0,306
g  az 9,81  0
z
b
2
tan  
 z  * tan   z  *0,306  0,306
b2
2
2
h A = h 0  z  1,5  0,306  1,81m
h B = h 0  z  1,5  0,306  1,19 m
53
PA =  .h   *( g  az )* hA  1000*(9,81  0)*1,81  17756 Pa
PB =  .h   *( g  az )* hB  1000*(9,81  0)*1,19  11674Pa
1,81
F1 =  .h G . A  9810*
*(1,81*2)=32138 N veya
2
PA * h A
17756*1,81
şekilden F1 =
.b 
*2=32138 N
2
2
F2 =
PB *h B
11674*1,19
.b 
*2=13892 N
2
2
54
(PA  PB ) * AB
(17756+11674)*2
F3 =
*b 
*2=58860 N
2
2
55
PA = PB =  .h   *( g  az )* h  1000*(9,81  3)*1,5  19215Pa
PA *h A
19215*1,5
F1 = F2 =
.b 
*2=28823 N
2
2
56
F3 = PA*AB*b  19215*2*2=76860 N
57
PA = PB =  .h   *( g  az )* h  1000*(9,81  3)*1,5  10215Pa
PA *h A
10215*1,5
F1 = F2 =
.b 
*2=15323 N
2
2
58
F3 = PA*AB*b  10215*2*2=40860 N
59
PA =  *( g  az )* hA  1000*(9,81  1,5)*1,73  19566Pa
PB =  *( g  az )* hB  1000*(9,81  1,5)*1, 27  14364Pa
PA * h A
19566*1,73
F1 =
.b 
*2= 33849 N
2
2
PB *h B
14364*1,27
F2 =
.b 
*2=18242 N
2
2
60
(PA  PB ) * AB
(19566+14364)*2
F3 =
*b 
*2 = 67860 N
2
2
61
Silindirik Bir Kapta Dönme
Sıvıyla kısmen doldurulmuş düşey bir silindirik kabı göz
önüne alalım. Şekilde gösterildiği gibi kapkendi ekseni
etrafında ω açısal hızıyla döndürülmektedir. Başlangıçtaki
geçici durumdan sonra sıvı, kapla beraber rijit cisim
şeklinde hareket edecektir. Herhangi bir şekil değiştirme
olmadığından bir kayma gerilmesi de oluşmaz ve her bir
akışkan parçacığı aynı açısal hızla hareket eder.
Kabın şekli silindirik olduğundan ve akışkan
parçacıkları dairesel hareket yaptığından
dolayı bu problem en iyi silindirik
koordinatlarda (r,θ, z) çözülür. z ekseni, kap
tabanından serbest yüzeye doğru kabın orta
çizgisi boyunca alınır. Dönme ekseninden r
mesafede bulunan ve ω sabit açısal hızıyla
dönen bir akışkan parçacığının merkezcil
ivmesi rω2 olup radyal olarak dönme
eksenine
doğru
(negatif
r
yönü)
yönlenmiştir. Diğer bir ifadeyle ar = - rω2 dir.
Dönme ekseni olan z ekseni etrafında simetri
vardır ve bu yüzden θ’ya bağımlılık yoktur.
Bu durumda P = P (r,z) ve aθ = 0 olur. Ayrıca
z
ekseni
doğrultusunda
hareket
olmadığından az = 0’dır.
Bu eğrisel yüzey bir parabol
şeklindedir ve serbest yüzey denklemi
zS =

2
2g
hc  h0 
r  hc
2
 R
2
2
4g
hc ,serbest yüzeyin kap tabanından dönme ekseni boyunca mesafesi
h0 ,dönme olmadan önce kaptaki akışkan yüksekliği
 Örnek 2.12: İçinde 3.5 m yüksekliğinde su bulunan şekildeki 1 m
yarıçaplı silindirik kap 5 rad/s açısal hızla kendi ekseni etrafında
döndürülüyor. Kaptaki suyun taşmaması için kap yüksekliği en az
kaç metre olmalıdır?
65
z ( x) =
 2 x2
2g
hc  h0 
 x
 R
2
2g
z (r )  H 
2
4g
2 2
z ( x) =
 hc
 h0 
 r
2 2
2g
 R
2
2
4g
 h0 
 R
2
4g
2
5212
5212
z (r ) =
 3,5 
2g
4g
z (r )  H  4,14 m
Kaynaklar
 Akışkanlar Mekaniği Ders Notları, Yrd. Doç. Dr. Serkan ŞENOCAK, Yrd. Doç. Dr. Selim ŞENGÜL, Atatürk
Üniversitesi, Mühendislik Fak. İnşaat Müh. Bölümü
 Akışkanlar Mekaniği, Frank M. White
 Akışkanlar Mekaniği, Temelleri ve Uygulamaları, Yunus A. Çengel, John M. Cimbala
 Akışkanlar Mekaniği ve Hidrolik, Prof. Dr. Mehmet Berkun
 Akışkanlar Mekaniği ve Hidrolik, Prof. Dr. Yalçın Yüksel
 Akışkanlar Mekaniğine Giriş, Young, D.F., Munson, B.R., Okiishi, T.H., Huebsch, W.W.
68