OREN3002 Statik ve Mukavemet

OREN3002
STATİK VE MUKAVEMET
ders notları
1
2. Bölüm
MUKAVEMET
ders notları
2
10. GERİLME KAVRAMI
3
10.1. Giriş
Mukavemeti dersinin temel hedefi, mühendislikte çeşitli makina
ve yük taşıyan yapıların analizi ve tasarımında gerekli bilgi ve
beceriyi sağlamaktır.
Bir yapının analiz ve tasarımı, gerilmeler ve deformasyonların
belirlenmesini içerir.
4
10.1. Yapı Elemanlarında Oluşan Gerilmeler
 Belirlenen iç kuvvetler, verilen bir yükün güvenli olarak taşınıp
taşınmayacağı hakkında bilgi vermez.
 Örneğin BC çubuğunun bu yüklemeyle kırılıp kırılmayacağı
aynı zamanda çubuğun kesit alanına ve çubuğun yapıldığı
malzemeye bağlıdır.
Şekil 10.1
 FBC iç kuvveti, kesitin A
alanına
etkiyen
yayılı
elemanter yüklerin bileşkesini
temsil eder.
 Bu yayılı yüklerin ortalama
yoğunluğu, kesitin birim
alanına etkiyen kuvvete, yani
FBC/A’ya eşittir.
5
 O halde, kırılma FBC kuvvetine, A kesit alanına ve çubuk
malzemesine bağlıdır.
 Birim alana etkiyen kuvvete veya verilen kesit üzerine etkiyen
yayılı kuvvetlerin yoğunluğuna o kesitteki gerilme adı verilir.
 P eksenel kuvvetine maruz A kesit
alanlı bir elemandaki gerilme,
yükün P büyüklüğü A kesit alanına
bölünerek elde edilir:
Şekil 10.2
6
 Metrik birim sistemine göre, P Newton (N) ile, A metre kare
(m2) ile σ gerilmesi de N/m2 ile ifade edilmektedir.
1 N/m2 = 1 Pa
7
10.2. Analiz ve Tasarım
 BC çubuğunun σem = 165 MPa emniyet gerilmeli bir çelikten
yapıldığını varsayalım. FBC = 50 kN olarak bulunmuştu.
Çubuğun çapının 20 mm olduğunu dikkate alarak uygulanan
yükle oluşan gerilmeyi belirleyelim:
 σ için bulunan değer, kullanılan çelikteki σem emniyet
gerilmesinden daha küçük olduğundan, BC çubuğunun
uygulanan yükü emniyetli bir şekilde taşıyabileceği sonucuna
varılır.
8
 Mühendisin işi, analiz ile sınırlı değildir. Yeni yapı ve
makinelerin tasarımı, yani istenen görevi yapacak uygun
elemanların seçimi de önemlidir. Tasarıma örnek olarak önceki
yapıya dönelim ve σem = 100 MPa emniyet gerilmeli
alüminyum kullanıldığını varsayalım. Kuvvet yine 50 kN
olduğundan,
 Buradan 26 mm veya daha büyük çaplı bir alüminyum
çubuğun yeterli olduğu anlaşılır.
9
10.3. Eksenel Yük – Normal Gerilme
 Önceki bölümde ele alınan BC çubuğunun B ve C uçlarına
etkiyen kuvvetler çubuk ekseni doğrultusundadır. Buna göre,
çubuk «eksenel yüke» maruzdur diyoruz (Şekil 10.2).
 Örneği, bir köprü kafesinin elemanlarındaki gerilme eksenel
yüke maruz oluşundan kaynaklanır.
 Gerilmeyi belirlemek için aldığımız kesit çubuğun eksenine
diktir. Elde edilen gerilme «normal gerilme» olarak tanımlanır:
 σ, kesitte yayılı iç kuvvetlerin bileşkesi olan P
büyüklüğünün kesitin A alanına bölünmesiyle
elde edilmiştir. Bu nedenle, kesitin belirli bir
noktasındaki gerilmeyi değil, kesit üzerindeki
gerilmenin
«ortalama
değerini»
temsil
etmektedir.
10
 Kesitin herhangi bir Q noktasındaki gerilmeyi
tanımlamak için, küçük bir ΔA alanını ele
almalıyız.
 ΔF büyüklüğünü ΔA’ya bölerek ΔA üzerindeki
gerilmenin ortalama değerini elde ederiz.
 ΔA’yı sıfıra yaklaştırarak Q noktasındaki
gerilmeyi elde ederiz:
Şekil 10.3
11
 Genelde, σ gerilmesi için kesitin
verilen bir Q noktasında elde edilen
değer, ortalama gerilme değerinden
farklıdır.
 Eşit ve zıt yönlü kuvvetlere maruz
ince bir çubukta bu değişim, tekil
yüklerin uygulama noktasından
uzaktaki bir kesitte küçüktür.
 Ancak uygulama noktası yakınındaki
kesitlerde bu değişim büyük
değerlere ulaşır.
Şekil 10.4
12
denkleminden, yayılı iç kuvvetlerin bileşkesinin büyüklüğünün
olduğu görülür.
 Şekildeki çubuğun her parçasındaki denge koşulları, bu
büyüklüğün tekil yüklerin P büyüklüğüne eşit olmasını
gerektirir. Böylece buradan,
elde edilir. Yani, her bir gerilme yüzeyinin altındaki hacim,
yüklerin P büyüklüğüne eşit olmaldır.
13
 Uygulamada, eksenel yüklü elemanlarda normal gerilme
dağılımının, yüklerin uygulama noktalarının hemen civarı hariç
olmak üzere, düzgün olduğu varsayılır. Gerilme değerleri
böylece σort’ya eşit olur.
 Ancak, kesitte düzgün bir gerilme
dağılımı olduğunu varsaydığımızda,
elemanter statiğe göre, iç kuvvetlerin
P bileşkesinin kesitin C ağırlık
merkezine uygulanması gerekir.
 Bu tip yüklemeye, «merkezi yükleme»
denir. Bunun kafes ve pim mafsallı
yapılarda bulunan tüm düzgün ikikuvvetli
elemanlarda
oluştuğu
varsayılacaktır.
Şekil 10.5
14
 Ancak, iki kuvvetli bir eleman,
eksenel
fakat
«dışmerkezli»
yüklemeye maruz ise, elemanın Şekil
b’de gösterilen parçasının denge
koşullarından, verilen bir kesitteki iç
kuvvetlerin, kesitin merkezinde
uygulanan bir P kuvveti ile M = Pd
momenti M kuvvet çiftine denk
olması gerektiğini buluruz.
 Kuvvetlerin dağılımı ve buna bağlı
olarak da gerilmelerin dağılımı
simetrik olmaz.
Şekil 10.6
15
10.4. Kayma Gerilmesi
 Önceki kesimde ele alınan iç kuvvetler ve
gerilmeler incelenen kesite dikti. Bir AB
elemanına P ve P’ enine kuvvetleri
uygulandığında çok farklı bir gerilme tipi elde
edilir. AC parçasının C kesitindeki iç
kuvvetlerin bileşkesi P’ye eşittir.
 Bu elemanter iç kuvvetlere «kesme
kuvvetleri» denir.
 P kesme kuvvetini A alanına bölerek, kesitteki
«ortalama kayma gerilmesi»ni elde ederiz:
Şekil 10.7
16
 Kayma gerilmesine, çeşitli yapısal elemanları ve makine
parçalarını birleştirmede kullanılan cıvatalar, pimler ve
perçinlerde sıklıkla rastlanır.
Şekil 10.8
17
 Plakalara F büyüklüğündeki çekme kuvveti uygulanırsa, EE’
düzlemine karşılık gelen cıvata kesitinde gerilmeler oluşur. Bu
cıvatanın «tek kesme» etkisinde olduğu söylenir. Kesitteki P
kesme kuvveti F’ye eşittir. Dolayısıyla ortalama kayma
gerilmesi:
Şekil 10.9
18
 A ve B plakalarını birleştirmek için C ve D bağlantı plakaları
kullanılmıştır. Buradaki cıvataların «çift kesme» etkisinde
olduğu söylenir. Serbest cisim diyagramlarından P = F/2
olduğu görülür. Ortalama kayma gerilmesi de şu şekilde
hesaplanır:
Şekil 10.10
19
10.5. Yataklarda Gerilme
 Cıvatalar, pimler ve perçinler birleştirdikleri elemanlarda
«yatak yüzeyi» veya temas yüzeyi boyunca gerilmeler yaratır.
P kuvveti, d çaplı ve t kalınlıklı bir yarım silindirin iç yüzeyine
yayılı elemanter kuvvetlerin bileşkesini temsil eder. Bu
kuvvetlerin ve karşılık gelen gerilmelerin dağılımı karmaşık
olduğundan, aşağıdaki basitleştirilmiş ifade ile «yatak
gerilmesi» hesaplanır:
Şekil 10.11
20
10.6. Analiz ve Tasarım Uygulamaları
 20 mm çaplı BC çubuğunun
yassı uçlarının 20x40 mm’lik
dikdörtgen kesitleri vardır. AB
kolunun kesiti 30x50 mm’lik
bir dikdörtgendir.
 B ucundan U-şekilli bir çatal
ile 30kN’luk bir yük asılmıştır.
AB kolu çift konsol içinde
geçen
pimle
A’da
bağlanmışken, BC çubuğu
C’de
tek
konsolla
bağlanmıştır.
 Tüm pimlerin çapı 25 mm’dir.
Şekil 10.12
21
10.6.1. AB Kolu ve BC Çubuğundaki Normal Gerilmelerin
Belirlenmesi
 BC çubuğundaki kuvvet FBC = 50kN (çekme), dairesel kesit
alanı A=314x10-6 m2 ve karşı gelen normal gerilme 𝜎BC = +159
MPa idi. Ancak, çubuğun yassı kısımları da çekme altındadır ve
deliğin yer aldığı en dar kesitte,
Şekil 10.13
22
 Artan yük altında, çubuğun silindirik kısmından değil,
deliklerden birinin yakınından kırılacağı açıktır. Çubuğun
tasarımı, yassı uçların enini veya kalınlığını arttırarak
iyileştirilebilir.
 AB kolundaki kuvvet FAB = 40kN (basınç), kolun dikdörtgen
kesit alanı A=1.5x10-3 m2 olduğundan, A ve B pimleri arasında,
normal gerilmenin ortalama değeri:
 A ve B’deki en küçük
kesitler gerilme etkisinde
değildir. Çünkü kol basınç
altındadır ve pimleri iter.
Şekil 10.14
23
10.6.2.
Çeşitli
Bağlantılardaki
Belirlenmesi
Kayma
Gerilmelerinin
 Bir cıvata, pim veya perçinde
kayma gerilmelerini belirlemek
için
öncelikle
elemanlar
üzerindeki kuvvetler açıkça
gösterilir.
 Çizimden DD’ düzlemindeki
kesme kuvvetinin P=50 kN
olduğu görülür.
Şekil 10.15
24
Pimin kesit alanı:
olduğundan, C’deki pimde kayma gerilmesinin ortalama değeri:
olarak bulunur.
25
A piminin çift kesmeye maruz kalmaktadır. SCD’ndan, P=20 kN ve
olarak hesaplanır.
Şekil 10.16
26
 B’deki pim, kol, çubuk ve çatalın uyguladığı kuvvetlerin
etkisinde beş parçaya bölünebilir. PE = 15 kN ve PG = 25 kN
olarak bulunur. Böylece en büyük kesme kuvvetinin 25 kN
olduğu ve en büyük kayma gerilmesinin G ve H kesitlerinde
oluşacağı görülür. Ortalama kayma gerilmesi:
Şekil 10.17
27
10.6.3. Yatak Gerilmelerinin Belirlenmesi
 AB elemanında A’daki nominal yatak gerilmesi; t = 30 mm, d =
25 mm ve P = FAB = 40 kN için:
 Konsolda A’daki nominal yatak gerilmesi; t = 2(25 mm) = 50
mm, d = 25 mm ve P = FAB = 40 kN için:
 AB elemanında B’de, BC
elemanında B ile C’de ve
konsolda
C’deki
yatak
gerilmeleri benzer yolla bulunur.
Şekil 10.18
28
10.7. Eksenel Yüklemede Eğik Kesitte Gerilme
 Eksenel
kuvvetler
elemanın
eksenine dik olmayan kesitlerde
hem normal gerilme hem de
kayma gerilmesi ortaya çıkarır.
 P kesite normal ve
bileşenlerine ayrılabilir:
dik
 Karşı gelen normal ve kayma
gerilmelerinin ortalama değerleri:
Şekil 10.19
29
A0 elemanın eksenine dik kesit alanı olmak üzere:
Şekil 10.20
30
10.8. Tasarımda Dikkate Alınması Gereken Konular
10.8.1. Kopma Mukavemetinin Belirlenmesi
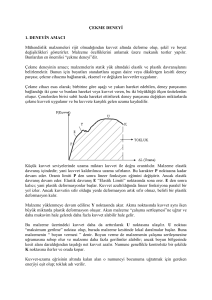
 Bir malzemenin yük altında nasıl davranacağının belirlenmesi
gerekir. Örneğin çelik bir çubuk, çekme cihazına bağlanarak
eksenel yük uygulanır.
 En büyük kuvvete ulaşıldığında numune kırılır ya da daha az
yük taşımaya başlar. Bu en büyük kuvvete, deney
numunesinin «kopma yükü» adı verilir. PU ile gösterilir.
Uygulanan yük merkezi olduğundan, PU çubuğun başlangıç
kesitine bölünerek «kopma normal gerilmesi» elde edilir. Bu
gerilme malzemenin «çekmedeki kopma mukavemeti» olarak
da bilinir:
31
 «Kopma
kayma
gerilmesi»
veya
«kesmede
kopma
mukavemeti»
genellikle dairesel tüpün burulması ile
belirlenir.
 Daha kolay ama daha az hassas bir
yöntem, şekilde görüldüğü gibi tek veya
çift kesmeye maruz kalacak şekilde
sabitlenen çubuğa uygulanan P yükünün
PU kopma yüküne ulaşıncaya kadar
arttırılarak uygulanmasını içerir.
 τU kopma kayma gerilmesi her iki
durumda da kopma yükünün kesmenin
oluştuğu toplam alana bölünmesiyle elde
edilir.
Şekil 10.21
32
10.8.2. Emniyet Yükü ve Emniyet Gerilmesi; Emniyet Katsayısı
 Bir yapı elemanı veya bir makine parçasının normal kullanım
koşullarında taşımasına izin verilen yük, kopma yükünden
oldukça küçüktür.
 Bu yük «emniyet yükü», «çalışma yükü» veya «tasarım yükü»
olarak adlandırılır.
33
10.8.3. Uygun Emniyet Katsayısının Seçimi
Verilen bir tasarıma uygun E.K. seçimi, birçok konuyla ilgili mühendislik
muhakemesi gerektirir:
1. Ele alınan malzemenin özelliklerinde meydana gelebilecek
değişimler.
2. Yapı veya makinenin çalışma ömrü süresince beklenen yükleme
sayısı.
3. Tasarımda planlanmış veya ileride ortaya çıkabilecek yükleme
çeşidi.
4. Meydana gelebilecek kırılma çeşidi.
5. Analiz yöntemlerinden ileri gelen belirsizlik.
6. Yetersiz bakım veya engellenemeyen doğal olaylar nedeniyle
ortaya çıkabilecek bozulma.
7. Elemanın yapının bütünlüğü açısından önemi.
34
11. GERİLME VE ŞEKİL DEĞİŞTİRME
35
11. GERİLME VE ŞEKİL DEĞİŞTİRME
11.1. Eksenel Yüklemede Normal Şekil Değiştirme
 Analiz ve tasarımın iki önemli özelliği çeşitli elemanlarda
uygulanan yükler sonucu oluşan gerilmeler ve bunların neden
olduğu deformasyonlardır.
 Yapının hedeflenen amacı yerine getirmesini engelleyecek
kadar büyük deformasyonlara maruz kalmasını önlemek
gerekir.
 Bu bölümde, eksenel yükleme halindeki çubuk, plaka gibi yapı
elemanlarının deformasyonlarını ele alınacaktır.
36
 Eksenel yüklemeye maruz bir çubuktaki normal şekil
değiştirme (ε), çubuğun «birim uzunluğundaki deformasyon»
olarak tanımlanır.
Şekil 11.1
Şekil 11.2
37
 Kesiti düzgün olmayan bir eleman halinde, gerilme eleman
boyunca değişir. Bir Q noktasındaki şekil değiştirme, deforme
olmamış küçük bir Δx elemanını göz önüne alınarak
tanımlanır:
Şekil 11.3
38
11.2. Gerilme – Şekil Değiştirme Diyagramı
 Malzemenin gerilme-şekil değiştirme diyagramı çekme deneyi
ile belirlenir. L0: ölçüm uzunluğu
Şekil 11.4
Şekil 11.5
39
Şekil 11.5
Şekil 11.6
 Malzemenin gerilme-şekil değiştirme diyagramından
malzemenin sünek mi gevrek mi olduğu anlaşılır.
40
Şekil 11.7
Şekil 11.8
Sünek malzemeler «akma» yetenekleri ile bilinirler.
σY: malzemenin «akma mukavemeti»
σU: malzemenin «maksimum! (kopma) mukavemeti»
σB: malzemenin «kırılma mukavemeti»
41
Şekil 11.9
 İnşaat çeliğinde akma noktası barizdir, diyagramdan
gözlenebilir. Alüminyum alaşımında ise akma noktası
«kaydırma» yöntemi ile belirlenir.
42
Şekil 11.10
Şekil 11.11
Şekil 11.12
 Gevrek malzemelerde maksimum mukavemet değeri ile
kırılma mukavemeti arasında fark yoktur.
 Gevrek malzemelerde kırılma anındaki şekil değiştirme, sünek
malzemelerden çok daha küçüktür.
43
 Bir malzemenin sünekliğinin standart bir ölçüsü uzama
yüzdesidir. Sık kullanılan bir çelikte %21’dir (Akma
mukavemeti 350 MPa ve 50 mm ölçüm uzunluğu).
 Diğer bir süneklik ölçüsü alan büzülmesidir. İnşaat çeliklerinde
genellikle %60-%70 arasında değişir.
44
Şekil 11.13. Betonun gerilme-şekil
değiştirme diyagramı.
 Çelikte akma mukavemeti hem
çekmede hem de basınçta
aynıdır.
 Akma noktasını aşan yüklemeler
sonucunda
eğriler
farklılık
gösterir.
 Basınçta boyun verme görülmez.
 Çoğu gevrek malzemede, basınç
kopma mukavemeti çekmedeki
kopma
mukavemetinden
büyüktür.
 Bu durum, çekmede malzemeyi
zayıflatan malzeme yapısındaki
mikroçatlaklar ile açıklanır.
45
Şekil 11.14. Tipik bir sünek malzeme için gerçek gerilme
gerçek şekil değiştirme diyagramı
 Önceki diyagramlardaki gerilmeler
bölünmesiyle elde edilmiştir.
Ancak, kesit alanı P artarken azalır.
σ = P/A0 : mühendislik gerilmesi.
σt = P/A: gerçek gerilme.
ε = δ/L0 : mühendislik şekil değiştirmesi.
εt: gerçek şekil değiştirme.
P
yükünün
A0 kesit
alanına
46
11.3. Hook Kanunu – Elastisite Modülü
 Hooke
kanununun
kullanılabildiği en büyük
gerilme
değerine,
malzemenin «orantı limiti»
adı verilir.
 Bariz akma noktasına sahip
malzemelerde
hemen
hemen akma noktası ile
çakışır.
 Diğer malzemeler için orantı
limitini tanımlamak kolay
değildir.
Şekil 11.15
47
 Yapı metallerinin özellikleri,
ısı uygulamasından ve üretim
sürecinden etkilenir.
 Şekilde görüldüğü gibi akma
mukavemeti,
kopma
mukavemeti ve son şekil
değiştirme arasında oldukça
büyük farklar vardır.
 Ama hepsi aynı elastisite
modülüne sahiptir.
Şekil 11.16
48
 Mekanik özellikler malzeme
doğrultusundan
bağımsız
ise malzeme izotropiktir.
 Özellikleri
ele
alınan
doğrultuya
bağlı
olan
malzemelere ise anizotropik
malzeme denir.
 Fiber takviyeli kompozit
malzemeler
anizotropik
malzemeye örnektir.
Ex ≠ Ey ≠ Ez
Şekil 11.17
49
11.4. Malzemenin Elastik ve Plastik Davranışı
 Bir numunedeki şekil değiştirme yük kaldırıldığında ortadan
kalkıyorsa, malzemenin elastik davrandığı söylenir.
 Elastik davranışın görüldüğü en büyük gerilme değeri,
malzemenin elastik limitidir.
 Bariz akma noktasına sahip malzemelerde elastik limit, orantı
limiti ve akma noktası temelde eşittir.
Şekil 11.18
50
 Akma noktasından sonra yük kaldırılırsa, şekil değiştirme sıfıra
dönmez. Bu durum kalıcı veya plastik deformasyon
oluştuğunu gösterir. Plastik deformasyonun gerilmeye bağlı
kısmına kayma, zamana bağlı kısmına sünme denir.
 Yeni
yükleme
eğrisinin
doğru
şeklindeki parçası, başlangıçtakinden
daha büyüktür.
 Bu durum, ilk yükleme sonucu oluşan
deformasyon
sertleşmesinin
sonucudur.
 Bununla birlikte, kopma noktası
değişmediğinden, D noktasından
ölçülen süneklik azalmıştır.
Şekil 11.19
51
11.5. Tekrarlı Yüklemeler ve Yorulma
 Gerilmeler elastik aralıkta
ise, verilen yük bir çok kez
tekrarlanabilir.
 Fakat yükleme sayısı belirli
bir değeri aştığında, kırılma
statik mukavemetten daha
düşük bir gerilme değerinde
gerçekleşir.
 Bu olay yorulma olarak
bilinir.
 Sünek malzemelerde bile
gevrek tabiata sahiptir.
Şekil 11.20
52
 Maksimum gerilmenin büyüklüğü azaldıkça, sürekli
mukavemet sınırı gerilmesine ulaşana kadar, kırılma için
gerekli döngülerin sayısı artar.
 Bir sanayi vincini taşıyan kiriş
25 yılda 2 milyon defa (bir iş
gününde 300 yükleme),
 320.000 km yol kat eden bir
aracın krank mili ½ milyar defa,
 Bir türbin kanadı ömrü
süresince birkaç milyar defa
yüklenebilir.
Şekil 11.21
53
 Alüminyum ve bakır gibi metallerde kırılma gerilmesi sürekli
bir düşüş göstermektedir. Böyle metaller için 500 milyon gibi
belli bir döngü sayısı, yorulma sınırı olarak tanımlanır.
Şekil 11.22
 Kırılma, mikroskobik bir çatlakta
veya benzer bir kusurlu kısımda
başlar.
 Tekrar
eden
yüklemeler
sonucunda, hasarsız kısım, yükü
taşıyamayacak kadar azaldığında
ani, gevrek kırılma meydana gelir.
Bu nedenle, yüzey durumu çok
önemlidir.
 Deniz suyu etkisiyle sürekli
mukavemet sınırına %50’ye varan
azalma beklenebilir.
54
11.6. Eksenel Yüklemede Deformasyon
 σ = P/A eksenel gerilmesi malzemenin orantı limitini
aşmıyorsa, Hooke kanunu uygulanabilir:
 Çubuk farklı kesit alanlarına ve/veya
farklı malzemeler içeriyorsa:
Şekil 11.23
55
 Değişken kesitli bir elemanda ε
şekil değiştirmesi Q noktasının
konumuna bağlıdır.
 ε = dδ/dx olarak ifade edilir.
 Buradan, dx uzunluğundaki
elemanın deformasyonu:
Şekil 11.24
 L toplam uzunluğu üzerinden
integral
alınarak
toplam
deformasyon elde edilir:
56
 Önceki durumlarda bir uç ankastre bağlanmıştı. Her iki uç da
hareket ederse, çubuğun deformasyonu, bir ucunun diğer
ucuna göre bağıl yer değiştirmesiyle ölçülür. B’nin A’ya göre
bağıl yer değiştirmesi:
Şekil 11.25
57
11.7. Sıcaklık Değişiminin Etkisi
 Düzgün kesitli, homojen bir AB çubuğu, pürüzsüz bir yüzeyde
serbestçe durmaktadır. Çubuğun sıcaklığı ΔT kadar arttırılırsa,
çubuk L uzunluğu ve ΔT ile orantılı olacak şekilde δT kadar
uzar.
α: termal genleşme katsayısı, 1/˚C
Şekil 11.26
58
 Sıcaklık değişiminden kaynaklandığı için, εT şekil
değiştirmesine termal şekil değiştirme adı verilir. Ele aldığımız
durumda bir gerilme meydana gelmez.
Şekil 11.27
 Başlangıçta gerilme veya şekil
değiştirme yok. Sıcaklık ΔT kadar
arttırılırsa, çubuk uzayamaz ve δT
sıfır olur. Dolayısıyla, εT = δT/L = 0.
 Fakat, sıcaklık artınca uzamaya
engel olmak için, mesnetler P ve P’
kuvvetleri uygular. Böylece, çubukta
gerilme oluşur.
59
 Problem statikçe belirsizdir. Uzama
sıfır olduğundan, mesnet tepkileri
hesaplanır.
 Süperpozisyon metodu için çubuk B
mesnedinden ayrılır.
Şekil 11.28
60
11.8. Poisson Oranı
 Bütün mühendislik malzemelerinde,
P eksenel çekme kuvvetiyle, kuvvet
doğrultusunda oluşan uzamanın
yanında, dik doğrultularda bir
daralma da olur. Aksi belirtilmedikçe,
ele alınan malzemeler hem homojen
hem de izotropik varsayılacak. Bu
nedenle εy = εz olmalıdır. Bu ortak
değere enine şekil değiştirme adı
verilir.
Şekil 11.29
61
62
11.9. Plastik Deformasyonlar
Gerilmeler akma mukavemetinden küçük olduğu sürece,
malzeme elastik davranır.
Akma mukavemetine ulaşılınca, akma başlar ve malzeme sabit
bir yük altında plastik deformasyonunu sürdürür.
 Yük
kaldırılırsa,
yükleme
eğrisinin AY başlangıç kısmına
paralel bir CD doğru parçası
boyunca boşaltma gerçekleşir.
 Yatay eksenin AD parçası, plastik
deformasyona karşı gelen şekil
değiştirmeyi gösterir.
Şekil 11.30
63
12. MALZEMELERİN MEKANİK ÖZELLİKLERİ
64
12. MALZEMELERİN MEKANİK ÖZELLİKLERİ
 Malzemelerin mekanik yükler altındaki davranışlarına
“Mekanik özellikler” adı verilir.
 Mekanik özellikler esas olarak atomlararası bağ
kuvvetlerinden kaynaklanır. Ancak bunun yanında malzemenin
iç yapısının (mikroyapı) da etkisi vardır. Bu sayede iç yapıyı
değiştirerek aynı malzemede farklı mekanik özellikler elde
etmek mümkün hale gelir.
 Metallerin mekanik özellikleri çeşitli yükleme şartlarında,
çeşitli deney parçaları ile incelenir.
65
 Mekanik tasarım ve imalat sırasında malzemelerin mekanik
davranışlarının bilinmesi çok önemlidir. Malzemelerin başlıca
mekanik özellikleri:
a) Çekme / basma (tensile /compression)
b) Sertlik (hardness)
c) Darbe (impact)
d) Kırılma (fracture)
e) Yorulma (fatigue)
f) Sürünme (creep)
66
12.1. Çekme Deneyi
 Malzemenin statik kuvvetler altında dayanımı ve mekanik
özelliklerinin test edilmesinde kullanılır.
Şekil 12.1. Çekme deneyi
67
 : Gerilme
 : Birim şekil değiştirme
F

Ao
l l  lo
 
lo
lo
Şekil 12.2. Çekme deneyinden
elde edilen F-L (Kuvvet Uzama) eğrisi
Şekil 12.3. F- L deki verilerinde
elde edilen - (Gerilme-Birim
uzama) eğrisi
68
 Malzemenin plastik şekil değiştirmeye (pşd) başladığı gerilme
değerine “akma dayanımı” adı verilir.
1. Belirgin akma göstermeyen malzemeler
2. Belirgin akma gösteren malzemeler
0.2
Belirgin olmaması
durumunda, akma
dayanımı % 0.2 kalıcı
pşd oluşturan gerilme
değerine eşittir.
p =0.002 = % 0.2
Şekil 12.4. Belirgin olmayan
akma noktası
Belirgin
akma
noktası
a
.
e
Şekil 12.5. Belirgin olan akma
noktası
69
Şekil 12.6. Gerilme – birim uzama diyagramı
70
Elastik şekil değişimi
•
•
•
•
Elastik bölgede Hook kanunu geçerlidir.
Gerilme ile birim uzama lineer olarak değişir.
Kuvvet kalkınca, elastik uzama ortadan kalkar.
E, Elastiklik Modülü, lineer kısmın eğimine eşittir
– Malzemenin
karakteristik
özelliğidir
(malzemeden
malzemeye değişir)
– E büyüdükçe malzeme daha rijit hale gelir yani gerilme ile
daha az şekil değişimi gösterir. Küçüldükçe daha elastik
davranır.
71
Hook Kanunu
Normal gerilme
Kayma gerilmesi
  G 
  E 
 = Normal gerilme
 = Birim şekil değişimi
E = Elastiklik modülü
Şekil 12.8
 = Kayma gerilmesi
 = Kayma birim şekil değişimi
G = kayma modülü
72
 Elastisite modülüne (E) etki eden parametreler:
• Kimyasal bileşim: E, bir malzeme özelliğidir. E, kimyasal
kompozisyondan etkilenir. Çelik, Alüminyuma göre daha rijittir.
• Ortam sıcaklığından etkilenir: Sıcaklık arttıkça E, azalır
• Isıl işlemden etkilenmez: Aynı çeliğin yumuşak hali ile
sertleştirilmiş hali aynı E’ye sahiptir.
73
Poisson Oranı
y

x 

      (izotropik malzemeler de) 
z 
z

Şekil 12.13
 Çekme yönünde malzeme uzarken buna dik yönde kısalma
gerçekleşir. Aradaki oran poisson oranı ile belirlenir.
 Elastik şekil değiştirmede metaller için 0.28 - 0.32 arasında
değişir. Genelde 0.3’tür.
 Plastik şekil değişiminde hacim sabit kalır ve poisson oranı 0.5
değeri alır.
74
Tablo 12.1. Bazı malzemelerin sıcaklık – elastik özellikleri
75
Plastik Şekil Değişimi
 Malzemelerin dayanımını ifade eden akma dayanımının üzerinde
gerilmeler uygulanması durumunda plastik şekil değişimleri (kalıcıgeri dönüşsüz) (PŞD) başlar.
 a
 Bu noktada PŞD, dislokasyonlar kaymaya başlamasıyla meydana
gelir.
 PŞD’de sıcaklık seviyelerine bağlı olarak farklı şekil değiştirme
mekanizmaları mevcuttur.
Bunlar;
1. Soğuk plastik şekil değiştirme,
2. Sıcak Plastik şekil değiştirme
3. Ilık Plastik şekil değiştirme
 Bu sıcaklık seviyeleri benzeş sıcaklık ile belirlenir.
76
Benzeş sıcaklık (homologous temperature):
TB 
 
 K
TÇ o K
TE
o
TE = Malzemenin erime sıcaklığı
TÇ = Çalışma sıcaklığı
0 < TB < 0.25 Soğuk Şekil Değişimi
0.25 < TB < 0.5 Ilık Şekil değişimi
0.5 < TB < 1
Sıcak Şekil değişimi
Oda sıcaklığı;
• Fe, Cu, Al gibi bir çok metal için soğuk şekil değişim bölgesi
iken
• Pb, Sn gibi düşük erime sıcaklığına sahip malzemeler için sıcak
şekil değişim bölgesidir.
77
Tablo 12.2. Çekme dayanım değerleri
78
Çekme diyagramından elde edilen veriler
•
•
•
•
•
•
•
•
•
E, Elastiklik modülü
a, Akma dayanımı
ç, Çekme dayanımı
k, Kopma gerilmesi
, Kopma uzaması
, Kesit daralması
ün, Üniform uzama
Statik tokluk
Rezilyans
Ayrıca her hangi bir noktada
• Elastik şekil değişim miktarı
• Plastik şekil değişim miktarı,
vs bulunabilir
79
Süneklik / Gevreklik / Tokluk / Rezilyans
• Süneklik: plastik şekil değiştirme kabiliyetini ifade eder. Bu
değerin büyümesi, malzeme kopana kadar daha büyük plastik
şekil değiştirme göstermesi anlamına gelir.
Kopma uzaması ve alan daralması parametreleri ile ifade
edilebilir.
• Gevreklik: Plastik şekil değiştirme kabiliyetinin olmaması
durumunu ifade eder. Eğri bazen elastik sınırda bazen de
elastik sınıra çok yakın bir noktada son bulur.
• Tokluk: Malzemenin kopana dek absorbe ettiği toplam enerjiyi
ifade eder.  -  eğrisinin altında kalan alana eşittir. Sünek
malzemelerin tokluğu gevrek malzemelere göre daha
yüksektir.
• Rezilyans: Malzemenin elastik şekil değişimi sırasında
depoladığı enerjidir.  -  eğrisinde elastik bölgenin altında
kalan alana eşittir.
80
Gerçek Gerilme - Birim Şekil Değiştirme
• Şu ana kadar hesaplamalarda başlangıç geometrik veriler
kullanıldı. Bu şekilde hesaplanan veriler “Mühendislik”
değerlerdir.
• Gerçekte plastik şekil değiştirme ile birlikte kesit alanı (hacmin
sabit kalması ile) sürekli azalır.
• Bu şekilde elde edilen verilere “Gerçek” değerdir.
• Özellikle metal şekillendirme uygulamalarında gerçek değerler
kullanılır.
81
Gerçek birim uzama.
Mühendislik birim uzama.
l l  lo l
 
 1
lo
lo
lo
l
  1
lo
PŞD de Hacim
sabit kalır.
Mühendislik
Gerilme. 
dl
d g 
l
l
dl
l
 g    ln
l
lo
lo

 g  ln(  1)
lo
Ao  lo  A  l  A  Ao 
l
Gerçek gerilme.
F

Ao
  g  F  F  l    (1   )
A
Ao  lo
82
 Gerçek değerlere göre çizilen
gerçek gerilme-birim uzama
eğrisine “Akama eğrisi” (Flow
curve) de denir.
• Elastik bölgede fark yoktur.
• Boyun
vermeden
sonra
homojen
olmayan
şekil
değişiminden dolayı uzama
hesaplanamaz.
Şekil 12.21. Gerçek ve mühendislik
- (Gerilme-Gerinme) eğrileri
83
Çekme diyagramı
1. Belirgin akma gösteren malzemelerin  -  diyagramları
2. Belirgin akma göstermeyen malzemeler  -  diyagramları
Şekil 12.24
84
Belirgin akma gösteren malzemeler
Çekme dayanımı
Pekleşme
Luders
bantlarının
oluşumu
Boyun verme
Büzülme
Kırılma-kopma
Şekil 12.25. Düşük karbonlu çelik belirgin akma noktası gösterir. Ayrıca 2 adet
akma noktası tanımlanmıştır: (a)Üst akma noktası, (b) Alt akma noktası.
85
Belirgin akma ve Cottrel atmosferi
• Bu olaya C, N gibi arayer atom kümelerinin dislokasyonların alt
kısmına yerleşip hareketlerini kilitlemesinin sebep olduğu
düşünülür.
• Bu arayer atom bulutuna “Cottrell atmosferi” adı verilir.
• C ve N den arındırılmış malzemeler belirgin akma göstermiyor.
86
• Üst akma noktası mekanik olarak bu kilitlerin kırılmasını ifade
eder. İlk akmanın meydana geldiği kayma bandının pekleşme ile
kilitlenmesinden sonra diğer düzlemlerde akma meydana gelir.
• Bu olayın kesit boyunca devamı ile luders bantları oluşur.
• Bu olay tamamlanınca homojen şekil değişimi başlar.
Üst akma noktası
Akma uzaması
Alt akma noktası
Lüders bantlar
Akmamış bölge
Şekil 12.26
87
Akma noktasından
sonra homojen PŞD.
(pekleşme / kesit
daralması dengesi)
Boyun verme
başlangıcı
Max noktadan
sonra heterojen
PŞD.(dengenin
bozulması)
Ç
0.2
 a
Kırılma
(kopma)
Şekil 12.29
0.002

88
Tablo 12.4. Çekme dayanım değerleri
89
Sertlik
Sertlik: Bir malzemenin yüzeyine batırılan sert bir cisme karşı
gösterdiği dirençtir.
Sertlik değerleri direk olarak malzemelerin dayanımları ile alakalı
olduğu için büyük önem taşır.
 Sertlik deneyi; malzemelerin dayanımları ile
ilgili bağıl değerler veren tahribatsız bir test
yöntemidir.
 Sertlik ölçme yöntemleri: Batıcı ucun
geometrisine
ve
uygulanan
kuvvet
büyüklüğüne göre:
– Brinell sertlik ölçme metodu
– Vickers sertlik ölçme metodu
– Rockwell sertlik ölçme metodu
Şekil 12.30
90
Sertlik ölçme yöntemleri
Şekil 12.31
91
Brinell Yöntemi
BSD 
Şekil 12.32
BSD
D
F
d
=
=
=
=
2F
 D [D  D2  d 2 ]
Brinell sertlik değeri
Bilye çapı
Uygulanan kuvvet
izin çapı.
• Standart test: 10mm çaplı sert bilye ve 3000kgf yük ile
yüzeye bastırılır.
• Yüzeyde bıraktığı iz dikkate alınır: izin çapı ölçülür.
• Metallerde BSD ile çek
arasında 400 BSD ye
kadar doğrusal ilişki
vardır.
2
BSD
(
kgf
/
mm
)
 ç (kgf / mm2 ) 
3
BSD (kgf / mm2 )
 ç ( MPa ) 
10
3
92
93
Vickers Yöntemi
• Batıcı uç tepe açısı 136o olan elmas
piramit yüzeye bastırılır.
• Yüzeyde bıraktığı iz dikkate alınır: Kare
şeklindeki izin köşegenleri mikroskopla
ölçülür.
• Sert veya yumuşak tüm malzemelere
d1  d 2
dort 
uygulanabilir.
2
• Kuvvet seçiminde malzeme kriteri yoktur.
1.72 F
• BSD değeri gibi çekme dayanımının
VSD 
2
tespitinde kullanılabilir.
d
ort
VSD = Birinell sertlik değeri
F
= Uygulanan kuvvet
dort = izin köşegen ortalaması.
94
Rockwell Yöntemi
 Batıcı uç olarak sertleştirilmiş çelik bilye veya elmas koni
kullanılır.
 Ucun yüzeye battığı derinlik dikkate alınır.
 Malzemeye göre uç/yük kombinasyonu seçilmelidir.
 Plastik malzemelerin ölçümü de yapılabilir: bir çok skalası
mevcuttur.
 C skalası; sert metaller için
kullanılır: 150kgf yük ve tepe açısı
120o olan elmas koni uç kullanılır.
 B; 100kgf yük ve 1/16” çapında
sert bilye kullanılır.
Şekil 12.33
95
• Ölçüm yüzeyleri temiz olmalıdır.
• Deney parçası yeterli kalınlıkta olmalı, kenara yakın ölçümler
yapılmamalı, birbirine yakın ölçümler yapılmamalı, en az 3
ölçüm yapılmalıdır.
96
Çentik Darbe Deneyi
 Çentik darbe deneyi, malzemeyi gevrek davranmaya iten
şartlar altında malzemenin dinamik tokluğunu ölçmek için
yapılır.
 Normal şartlarda sünek malzeme
•Üç eksenli yükleme hali
•Düşük sıcaklıkta zorlama
•Kuvvetin ani uygulanması (darbe)
durumlarında plastik şekil değişimine imkan bulamaz ve gevrek
davranış gösterirler.
 Bu şartlardan biri veya bir kaçı gerçekleşmişse malzeme
gevrek davranabilir.
 Bu amaç için Charpy (üç noktadan eğme) veya Izod (ankastre
eğme) deneyleri mevcuttur.
 Darbe enerjisine etki eden faktörler: dayanım, kristal yapı,
sıcaklık ve kimyasal bileşim.
97
•Belli bir potansiyel enerjiye
sahip kütle V-çentik açılmış
numuneye çarptırılır.
•Numunenin kırılması için
gereken enerji “Darbe
Enerjisi - Ek” saptanır.
Ek  mg  (h  h' )
Şekil 12.34
98
99
Sünek-gevrek geçiş sıcaklığı
Tg
Emax  Emin
T @
2
Şekil 12.35
100
101
13. DAYANIM BİLGİSİ
102
13. DAYANIM BİLGİSİ
13.1. Basma Dayanımı
 Bir cismin ekseni doğrultusunda etki eden kuvvetler birbirine
yaklaşırsa cismin bünyesinde (iç yapısında) bir basılma
(basınç) meydana gelir. Basılma anında cismin bünyesindeki iç
kuvvetlerin birim alanına gelen miktarına da “basma
gerilimi/dayanımı” denir.
103
 Beton, taş, dökme demir, çelik, odun gibi malzemelere basma
deneyleri yapılarak bu malzemelerin basma dayanımları
ölçülür. Örneğin bir binanın kolonundan alınan küçük bir
beton kesite basılma kuvveti uygulanarak malzemenin
dağılmadan dayanabileceği basılma gerilim miktarı ölçülebilir.
Gevrek
ve
yumuşak
malzemelerde deney sonuna
kadar basınç temini zordur.
Gevrek
malzeme
deney
sırasında kırılıp dağılabilir.
Yumuşak malzeme ise ortadan
Şekil 13.1. Basma deneyi
şişerek fıçı şeklini alır.
104
 Bir cisme bir kuvvet etki yaptığı zaman cisim kısalmaya çalışır.
Burada dik gerilmeler meydana geldiğinden aşağıdaki eşitlik
kullanılır.
 Bu şekilde çalışan elemanlar,
pres milleri, kalıp zımbaları,
piston kolları olabilir. Bir cisim
diğer
cisim
üzerine
etki
yaptığında basınç meydana gelir.
 Bu basınç ile cisimde ezilme
oluşur.
 Basınç ve ezilmede, değme
yüzeyinin konumu ve büyüklüğü
önemlidir.
Şekil 13.2. Basma kuvveti
105
 Makine tasarımında üretilen hareket ve kuvvetler; mil, kol,
dişli, vida vb. elemanlarla kullanma yerine taşınır.
 Bu taşıma sırasında üretilen kuvvet sisteme aynen yansımaz.
 Makine elemanları montaj durumuna göre bileşenleri kadar
etkilenir. Buna dolaylı yük denir.
106
Şekil 13.3. Dolaylı (a ve b), açılı (c) yük
 Şekildeki dikdörtgen kesitli
bir elemana etkiyen kuvvet
gösterilmektedir.
Bu
durumda etkiyen doğrudan
yük Fy aşağıdaki gibi
hesaplanır.
Şekil 13.4. Açılı yük ve dönüşümü
107
13.2. Çekme Dayanımı
 Aşağıda görülen şekilde test çubuğuna etki eden kuvvetler,
eksen boyunca birbirinden uzaklaşırlarsa çekme ya da çekilme
meydana gelir. Bununla ilgili dayanıma da “çekme dayanımı”
denir. Cismin çekme dayanımı, molekül yapısı ve kesit alanı
(A0) ile ilgilidir.
E.K.S = S = Emniyet katsayısı
Şekil 13.5. Test çubuğu ve kesit alanı
108
 Makine elemanları boyutlandırılırken şekil değişikliklerinin, bu
elemanların özelliklerinin bir kısmını ya da hepsini
kaybettirmemesine dikkat edilir. Yapılan hesaplarla zarar verip
vermeyeceği kontrol edilir.
 Malzemelerin şekil değiştirme ve mekanik özelliklerinin
tespitinde en sağlıklı sonuç alınan deney, çekme deneyidir.
 Bu deneylerde, standart çubuklar kullanılır.
 Bu çubuklar; TS 138 ve DIN 50125’te verilen biçim ve
ölçülerde makinelerde işlenerek elde edilir.
 Hooke kanuna göre; elastiklik sınırları içinde kalmak şartı ile
bir malzemede meydana gelen şekil değiştirmeler, gerilmeler
orantılıdır.
 Kuvvet ne kadarsa uzama da o kadardır.
109
 Hooke kanununa göre, elastiklik sınırları içinde olmak koşulu
ile malzemede meydana gelen şekil değiştirmeler, bunlara
karşılık gelen gerilmeler ile orantılıdır.
tgα eğimine, malzemenin elastiklik modülü (E) denir.
Şekil 13.6. Malzemede uzama
110
 Çekme deneyi sırasında malzemenin boyu uzarken, kesit alanı
daralır. Boyca birim uzamanın ence birim daralmaya oranı,
Poisson oranını verir.
111
13.3. Kesme Dayanımı
 F kuvvetleri parçanın eksenine dik durumda birbirine doğru
yaklaşırsa makaslama dolayısı ile kesilme olayı meydana gelir.
Burada oluşan dayanıma kesilme dayanımı denir.
Şekil 13.7. Kesilme gerilmesi
112
13.4. Eğilme Dayanımı
 Prizmatik çubuk ya da miller eksenlerine dik kuvvetlerle
yüklenirlerse çubuk ya da mil kesitinde kesme kuvveti ve
eğilme momenti meydana gelir. Eğilme momenti sonucunda
çubuk eğilir. Bununla ilgili dayanıma da eğilme dayanımı denir.
Şekil 13.8. Kesme deneyi
113
Eğilme Momenti (Mb)
 Eksenleri dik olarak yüklenen kirişin, eğilerek bir kavis şeklini
almasına neden olan momente, eğilme momenti denir.
 Bir sistemde momentin bulunabilmesi için uygulanan kuvvetin
kuvvet kolu ile çarpılması gerekir.
Mb = F L
 Ancak değişik aralıklarla ve birden fazla kuvvetlerle yüklenmiş
kirişlerde basit eğilme hali olmadığından bu kirişlerde
diyagramlar çizilir.
 Kritik nokta ve karşısında bulunan maksimum moment eğilme
momenti (Mb) olarak alınır.
114
Şekil 13.9. Eğilme momenti
115
 Eğilen bir kirişin dış yüzeyi incelendiğinde iç kısmındaki liflerin
kısaldığı ve burada basma gerilmesi, dış kısımdaki liflerin
uzadığı, burada ise çekme gerilmesi meydana geldiği görülür.
 Bu normal gerilmelerin kesite yayılı hali, eğilme gerilmesini
meydana getirir.
 Eğilme halinde dayanım momenti (W) kesitin şekline (kare,
dikdörtgen, daire, üçgen, vb.) ve kuvvetin geliş yönüne bağlı
olarak hesaplanır.
116
Tablo 13.1. Temel şekillerin dayanım ve atalet momentleri
117
Dayanım Momentinin Belirlenmesi
 Bir ankastre (konsol) kiriş, F kuvveti ile yüklendiğinde eğilme
meydana gelir.
 Kirişin ağırlık merkezinden geçen eksene, nötr eksen (tarafsız)
adı verilir.
 Bu durumda, tarafsız eksen eğri hâline gelir.
 Daha önce de bahsedildiği gibi kirişin üst kısmındaki lifler uzar,
alt kısmındaki lifler kısalır.
 Buradaki gerilmeler en büyük maksimum değerini alır.
 Hooke Kanunu’na göre; en büyük uzama, en büyük gerilme
sınırında meydana gelir.
118
 Kesitin dayanabileceği en büyük moment, eğilme momentidir
(max Mb).
 Ancak bu, makine elemanlarının boyutlandırılmasında yeterli
olmaz. Boyutlandırma işleminde, dayanım momenti (W)
kullanılır.
119
13.5. Burulma Dayanımı
 Bir ucundan sabitlenmiş prizmatik ya da silindirik bir çubuk,
ekseni doğrultusunda dik bir düzlemde etki yapan kuvvet çifti
ile diğer ucundan döndürmeye zorlanırsa döndürme momenti
(Md) meydana gelir. Pratikte buna, “tork” denir.
 Çubuk kesitinin, ekseni etrafında dönmesine “burulma”,
meydana gelen dayanıma da “burulma dayanımı” denir.
Şekil 13.10. Burulma
120
121
122
13.6. Burkulma Dayanımı
 Basılma dayanımında incelenen çubukların boyları kısa ve
kesit alanları büyüktü. Burkulma dayanımında ise ele alınan
çubukların boyları, kesit alanlarına göre çok büyük olur.
 Kesit alanları küçük, boyları uzun çubuklara, “narin çubuk”
denir.
 Narin
çubuklar
eksenleri
doğrultusunda yüklendiklerinde (F),
bir eksenel sapma (a) yapar.
 Bu olaya “burkulma”, burkulmaya
başlama sınırında meydana gelen
maksimum dayanıma da “burkulma
dayanımı” denir.
Şekil 13.11. Narin çubuk
123
Kritik Yük (Fk)
 Şekildeki narin çubuğun ağırlığı ihmal edilsin. Başlangıçta
küçük bir F kuvveti uygulanmaya başlanırsa eksenel sapma
görülemeyecek kadar az olur. Kuvvetin artırılması sonunda bir
yaylanma hareketi, devamında eğilme ve bir süre sonra da
kırılma meydana gelir. Bu olaya “burkulma = flambaj”, burada
tam kırılma sınırında etki kuvvetine de kritik yük (Fk) adı verilir.
Burkulma (Flambaj) Boyu (Lk)
 Burkulma uzunluğu; çubuğun etkilendiği kritik yük belliyken
kesit alanı da göz önüne alınarak tespit edilen çubuk
uzunluğudur. Şekilde görülen çubuk, bir ucu mafsallı, diğer
ucu dayatılmış olduğundan, Lk = L alınır. Bu durumda çubuğun
konumuna göre, Lk değerlerinin değiştiği anlaşılır. Şekilde dört
konuma göre burkulmaya çalışan çubuklar verilmiştir.
124
Şekil 13.12. Burkulma şekilleri
125
Elastiklik Modülü (E)
 Malzemelerin elastiklik modülü olan (E), Hooke Kanunu’nda
açıklanmıştı. Örnek olarak en çok karşılaştığımız malzeme olan
çeliğin elastiklik modülü, E = 2.1x106 daN/cm2’dir.
Narinlik Derecesi ( )
 Narinlik derecesi l = lamda; burkulma dayanımında,
çubukların kesit boyları ve uzunluğu ile ilgili bir büyüklüktür.
Önce jirasyon çapını bilmek gerekir (rj).
126
127
Euler (Oyler) Metodu
 Euler metodu dolayısı ile formülü, Hooke Kanunu’nun geçerli
olduğu elastik bölgenin altındaki durumlarda geçerlidir.
 Buna göre Euler formülü;
128
129
13.7. Birleşik Dayanım
 Makine elemanlarının çalışmaları sırasında dayanımlı olmaları
esastır.
 Bir dayanım şekline göre hesaplanmış makine elemanının,
çalışma süresince hep aynı yüklemede kalması gerekir.
 Ancak makine elemanları çalışırken genellikle iki ya da daha
fazla dayanım şekilleri ile karşılaşırlar.
 Bu durumda, yalnız bir dayanım şekline göre hesaplanmış
makine elemanı, yeteri kadar dayanımlı olmaz.
 Makine elemanları üzerinde, aynı anda birkaç dayanım
şeklinin bir arada olmasından meydana gelen dayanıma
“birleşik dayanım” denir.
130
13.7.1.
Çekme-Basma ve Eğilmeye Zorlanan Makine
Elemanlarının Toplam Geriliminin Hesaplanması
 Bir çubuk, Şekilde görüldüğü gibi eksenine paralel ve a kadar
uzaklıkta bir F kuvveti ile zorlanmaktadır. Eksantrik adı verilen
bu kuvvet çubuğa, bir kuvvet çifti şeklinde etki yapar. Bu
durumda çubuk, dış kuvvetin etki yönüne göre çekme ya da
basma ile birlikte eğilmeye çalışır. Bu birleşik dayanım
durumu, basit dayanım şekillerine indirgenir.
 Çubuk, yalnız çekme ya da basmaya çalışıyormuş gibi
düşünülür. Her iki durumda da çubuk kesit alanında normal
gerilmeler oluşur. Normal gerilmeler, kesit alanına eşit
dağılmış ve aynı yönlüdür. Ancak çekme ya da basma şekline
göre çözümlerde genellikle tepki yönleri esas alındığından
buna göre değişebilmektedir.
131
Şekil 13.13. Birleşik dayanım
132
 Çubuk eksenine paralel ve a kadar uzaklıktaki kuwet (F),
eğilme momentini (Mb) meydana getirir. Mb= F.a (daN. cm)
Eğilme yönüne göre çubuğun bir tarafında uzama, bir
tarafında kısalma meydana gelir. Eğilmeden oluşan ve
uzamaya neden olan çekme gerilmeleri + pozitif, basılma
gerilmeleri de - negatif işaretlidirler. Şekildeki diyagramda da
tarafsız eksenden itibaren farklı yönlerde gösterilir.
 Ayrıca burada kesilme gerilmeleri de meydana gelir. Ancak
bunlar küçük değerde olduklarından dikkate alınmazlar.
Çubuğa normal kuvvet ile eğilmenin birlikte etki etmesinden
meydana gelen toplam gerilme;
133
Şekildeki kesitin M noktasındaki normal gerilme:
134
13.7.2. Eğilme ve Burulmaya Zorlanan Makine Elemanlarının
Toplam Geriliminin Hesaplanması
 Miller, muylular ve krank milleri gibi makine elemanları güç ve
hareket ilettiklerinden burulma ile birlikte eğilmeye de
zorlanır. Eğilme momenti ile burulma momentinin birlikte
bulunması durumuna “burulmalı eğilme” denir. Teknik alanda;
talaş kaldırma, cıvata sıkma vb. işlemlerde de aynı durum
yaşanır.
 Şekilde bir mil, serbest ucundan
eksantrik
bir
kuvvetle
döndürülmeye
zorlanıyor.
Burada, burulma momenti ve
eğilme
momenti
birlikte
meydana
gelmiştir.
Kesme
kuvveti ise ihmal edilmiştir.
Şekil 13.14. Eğilmeli burulma
135
 Eğilme sonucu oluşan Gmax ve burulmadan dolayı meydana
gelen kayma gerilmesi Tmax milin dış yüzeyinde meydana
çıkar (Şekil 13.14-b). Bu iki gerilmenin toplamı, maksimum
gerilme bileşkesini verir. Şekil 13.14-a’ya göre en tehlikeli
kesit, ankastre dayanağının en üst ve en altında meydana
gelir.
 Bu tehlikeli kesitin dış kısmından alınan A yüzey elamanının
Mohr dairesi üzerinde incelenmesi, formül çıkışlarında ve
anlaşılmasında kolaylık sağlar (Şekil 13.15).
136
Şekil 13.15. Mohr dairesi
137
 Dayanım esaslarına göre en büyük gerilmeler dikkate alınır.
Şekil 13.15 incelenirse; BF gerilmesinin BA gerilmesinden, EH
gerilmesinin de AC gerilmesinden büyük olduğu anlaşılır.
Bunlara göre, milin boyutlandırılmasında büyük gerilmeler
işleme konulur.
138
139