GERİLME…
Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve
momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil
ettiği ifade edilmişti. Cisimlerin mukavemeti çalışmalarında, bu dağılımın
elde edilmesi birinci derece öneme sahiptir. Bu problemi çözmek için gerilme
kavramının tesis edilmesi gerekir.
GERİLME…
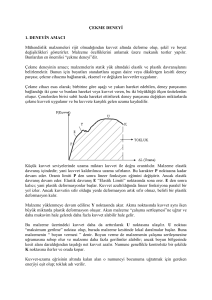
Kesilmiş alanı, şekil görülen A gibi küçük alt alanlara parçalamakla başlayacağız. A
alanını daha küçük çok daha küçük boyutlara bölerken malzeme özellikleriyle ilgili iki
kabul yapmamız gerekir. Malzemeyi sürekli ortam yani düzgün dağılımlı veya
boşluksuz kabul edeceğiz.
A alanına etki eden sonlu ancak çok küçük F kuvveti şekilde gösterilmiştir. Diğerleri
gibi bu kuvvette tek bir doğrultuya sahip olmakla birlikte detaylı inceleme yapabilmek
için onu sırasıyla alana teğet, teğet ve normal Fx, Fy ve Fz bileşenleriyle
değiştireceğiz. A sıfıra yaklaşırken F ve bileşenleri de sıfıra yaklaşır; her halükarda
kuvvetin alana oranı sonlu bir limite yaklaşacaktır. Bu oran gerilme olarak adlandırılır
ve ifade edildiği gibi bir noktadan geçen belirli alana etki eden iç kuvvet yoğunluğu
olarak tanımlanır.
GERİLME…
Normal Gerilme. A ya dik olarak etki eden kuvvet yoğunluğu normal gerilme
olarak tanımlanır ve (sigma) ile sembolize edilir. Fz alana dik olduğundan
=
∆ →
∆
∆
Eğer normal kuvvet veya gerilme, şekilde görüldüğü gibi, A alanına “çeki”
uyguluyorsa çekme gerilmesi, buna karşı “bası” uyguluyorsa basma gerilmesi
olarak adlandırılır.
GERİLME…
Kayma Gerilmesi. A ya paralel olarak etki eden kuvvet yoğunluğu
kayma gerilmesi olarak tanımlanır ve (tau) ile sembolize edilir. Burada,
kayma gerilmesi bileşenleri olacağından
=
=
∆ →
∆
∆
∆ →
∆
∆
Bu notasyonda, alt indis z alan A nın doğrultusunu tanımlarken x ve y
her bir kayma gerilmesinin etki ettiği eksenleri göstermektedir.
GERİLME…
Birimler. Gerilme, birim alandaki kuvveti tanımladığından Uluslararası
standart veya SI birim sisteminde, hem normal hem de kayma gerilme
bileşenlerinin büyüklükleri temel birimlerle metre karedeki Newton
cinsinden kuvvet (N/m2) olarak belirlenir. Pascal (1Pa =1N/m2) olarak
adlandırılan bu birim oldukça küçük bir büyüklüğü ifade ettiğinden
mühendislik çalışmalarında k ön eki ile sembolize edilen kilo- (103), M ile
sembolize edilen Mega- (106) ve G ile sembolize edilen Giga- (109) gibi daha
gerçekçi gerilme büyüklükleri ifade edilirken ön ekleriyle birlikte kullanılır.
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
Bu bölümde, şekilde gösterildiği gibi eksenel yüklü çubuğun kesit alanına etki
eden ortalama gerilme dağılımını belirleyeceğiz. Uzunluğu boyunca bütün
kesitleri aynı olduğu için bu çubuk prizmatiktir. Çubuğun malzemesi hem
homojen hem de izotropik olması durumunda, çubuğa kesit alanın
merkezinden geçen P yükü uygulandığında, gösterildiği gibi uzunluğunun
merkez bölgesi boyunca düzgün olarak şekil değiştirecektir.
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
Homojen malzeme hacmin her yerinde aynı fiziksel ve mekanik özelliklere
sahip iken izotrop malzeme ise her doğrultuda aynı özelliklere sahiptir. Çoğu
mühendislik malzemelerine burada olduğu gibi yaklaşım uygulanarak hem
homojen hem izotrop kabul edilebilir.
Ahşapta olduğu gibi anizotrop malzemeler farklı doğrultularda farklı
özelliklere sahip olmakla birlikte, anizotropi çubuk ekseni boyunca
yönlenmişse, eksenel P yüküne maruz çubuk yine düzgün deforme olacaktır.
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
Çubuk boyunca kesim yaparsak çubuğu iki parçaya böleriz. Bunun sonucu
olarak, denge şartı kesitteki bileşke normal kuvvetin P ye denk olmasını
gerektirir. Malzeme düzgün deforme olduğundan kesit sabit normal gerilme
dağılımına maruz olması gerekir.
Sonuç olarak, kesit alandaki her bir küçük A alanı F= A kuvvetine
maruzdur. Bütün kesit üzerine etki eden bu kuvvetlerin toplamı, kesitteki
bileşke iç kuvvet P ye eşit olmalıdır. Eğer A→dA olduğunu kabul edersek bu
durumda F→dF olacaktır.
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
+↑
=∑
;
=∫
∫
=
=
Burada,
= Kesit alandaki herhangi bir noktadaki ortalama
normal gerilme
P = Kesit alanın merkezi boyunca etki eden bileşke
normal iç kuvvet. P kesim metodu ve denge
denklemleri kullanılarak belirlenir.
A = Gerilmenin belirleneceği çubuğun kesit alanı
İç yük P, çubuk kesitinin ağırlık merkezinden geçtiği için düzgün gerilme
dağılımı x ve y eksenleri etrafında sıfır moment meydana getirecektir.
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
Denge. Eksenel yüklü çubuğun kesitinin her bir noktasındaki küçük hacim
eleman üzerinde sadece normal gerilme oluşacağı aşikârdır. Hacim elemanın
dengesi göz önüne alınır ve kuvvetlere denge denklemleri uygulanırsa,
∑
= ;
∆
−
∆
=
=
Bir başka ifadeyle, eleman üzerindeki iki normal gerilme bileşeni eşit
büyüklükte fakat zıt yönde olmalıdır. Bu tek eksenli gerilme olarak tanımlanır.
Bileşke iç kuvvet P nin büyüklüğü grafik olarak, gerilme diyagramı altındaki
hacme eşittir. Yani, P=A (Hacim=TabanYükseklik). Buna ilaveten, moment
dengesinin sonucu olarak bu bileşke hacmin ağırlık merkezinden geçer.
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
Eksenel Yüklü Çubukta Ortalama Normal Gerilme
Analizde, hem iç kuvvet P hem de kesit alan A çubuğun ekseni
boyunca sabit olduğu için çubuğun uzunluğu boyunca normal gerilme
= P/A da sabittir.
Bununla birlikte, çubuk ekseni boyunca birden fazla dış yüke maruz
kalabilir veya kesitinde değişim meydana gelebilir. Yani, çubuktaki
normal gerilme bir kesitten diğerine değişebilir.
Eğer maksimum ortalama normal gerilme belirlenecekse, P/A oranının
nerede maksimum olacağının belirlenmesi gerekir. Bunu yapmak için
çubuk boyunca farklı kesitlerdeki iç kuvvet P belirlenmelidir.
Bu gibi durumlarda, eksenel veya normal kuvvet diyagramı çizilerek bu
değişimin gösterilmesi faydalı olabilir. Özel olarak da, bu diyagram
normal kuvvet
nin kiriş uzunluğu boyunca x bağlı pozisyonunun
grafiğidir. İşaret kabulüne uygun olarak elemanda çekmeye sebep olan
P pozitif, basınca sebep olan P ise negatiftir.
ÖRNEK
80 kg lamba şekil (a) görüldüğü gibi AB ve BC çubuklarıyla taşınmaktadır. AB
çubuğunun çapı 10 mm ve BC çubuğunun çapı 8 mm ise her bir çubukta oluşan
ortalama normal gerilmeyi hesaplayınız.
İç kuvvetler: Öncelikle her bir çubuktaki eksenel kuvvetler belirlenir.
Lambanın serbest cisim diyagramı şekilde (b) gösterilmiştir. Denge
denklemlerinden,
→
↑
= ;
= ;
⁄
⁄
=
−
+
°=
°−
.
,
.
=
=
.
ÖRNEK
=
.
=
.
Ortalama Normal Gerilme
.
=
=
( .
=
= .
)
.
( .
)
= .
ÖRNEK
NOT: AB çubuğunun kesitine etki eden ortalama normal gerilme dağılımı
şekil (c) de ve kesit üzerindeki bir noktada gerilme durumu birim hacim
elemanda şekil (d) görülmektedir.
ÖRNEK
Şekil (a) daki çubuk sabit 35 mm genişliğe ve 10 mm kalınlığa sahiptir.
Görülen yüklere maruz çubukta oluşan maksimum ortalama normal
gerilmeyi belirleyiniz.
ÖRNEK
İç Yükler: AB, BC ve CD bölgelerinde eksenel iç kuvvetler farklı büyüklükte
ancak sabit değere sahiptirler. Kesim metodu kullanılarak bu yükler şekil (b)
de belirlenmiştir.
ÖRNEK
Bileşke normal iç kuvvetlerin gösterildiği bu sonuçlar grafik olarak
gösterilmiştir Şekil (c). İncelenirse, en büyük iç kuvvet BC bölgesinde olup
büyüklüğü PBC = 30 kN dur. Çubuğun kesit alanı sabit olduğundan en büyük
ortalama normal gerilme çubuğun bu bölgesinde oluşur.
=
(
=
)
.
Ortalama Kayma Gerilmesi
Bu gerilmenin nasıl oluştuğunu göstermek için şekil (a) daki çubuğa
uygulanan F kuvvetinin etkilerini ele alalım. Eğer mesnetler rijit ve F kuvveti
de yeterince büyükse, kuvvet çubuğun şekil değişimine ve AB ile CD
düzlemleri boyunca kayarak hasar (kırılma) oluşumuna sebep olacaktır.
Çubuğun mesnetli orta kısmının serbest cisim diyagramı, Şekil (b) parçayı
dengede tutabilmek için her bir kesite V=F/2 kesme kuvveti uygulanması
gerektiğini gösterir.
Ortalama Kayma Gerilmesi
Kesme kuvveti tarafından oluşturulan her bir kesilmiş alana yayılı ortalama
kayma gerilmesi şu ifadeyle tanımlanır.
=
Burada,
ort= Kesit üzerindeki her noktada aynı olduğu kabul edilen ortalama kayma
gerilmesi
V= Denge denklemlerinden elde edilmiş kesitteki iç kesme kuvveti
A= Kesit alanı
Bu traktörün parçasının mafsal bağlı
olarak birleştirilmesinde kullanılan A
pimi, B ve C deki pimin iki yüzeyinde
kayma gerilmesi oluşturduğu için çift
kesmeye maruzdur.
İzin Verilen Tasarım Gerilmesi (Emniyetli Gerilme)
Makine veya yapı elemanının güvenliğini garanti etmek için uygulanan
yükün yapının tam yükte taşıyabileceğinden daha küçük bir yükle
sınırlandırılması gerekir. Bunun yapılması için çok sayıda sebep vardır.
Yapının veya makinanın planlanan boyutları, parça bileşenlerinin üretimdeki
veya montajdaki hatalardan dolayı tam doğru olmayabilir. Tasarımda dikkat
alınmayan bilinmeyen titreşimler, darbe veya kazara yükler oluşabilir.
Atmosferik korozyon, çürüme veya hava şartları servis süresince malzemenin
bozulmasına yol açabilir.
Yapı elemanı için izin verilen yükün belirlenmesinin bir yöntemi de emniyet
katsayısı olarak adlandırılan rakam kullanılmasıdır. Hasar (akma)
oluşturacak Fha yükün izin verilen (emniyetli) Fem yüke oranına emniyet
katsayısı denir. Burada, Fha malzeme için yapılan testlerden bulunur.
Yukarıda bahsedilen bütün belirsizlikler göz önüne alınarak elemanın benzer
geometri ve yükleme şartları altında kullanılması durumunda tecrübelere
dayanılarak emniyet katsayısı seçilir. Matematiksel olarak,
EK = Fha / Fem
İzin Verilen Tasarım Gerilmesi (Emniyetli Gerilme)
Eğer elemana uygulanan yük, doğrudan gerilme =P/A veya ort=V/A da
kullanıldığı gibi ilişkiliyse, emniyet katsayısı, ha (veya ha) hasar gerilmesinin
emniyetli gerilmeye em (veyaem) oranı olarak belirlenir.*Burada alan A
sadeleştirilirse,
E.K = ha /em veya
E.K = ha /em
Bu denklemlerin herhangi birinde, potansiyel hasarın önüne geçmek için
emniyet katsayısı 1 den büyük olmalıdır. Emniyet katsayısı için seçilen özel
değerler, makine veya yapı elemanının kullanım amacına ve kullanılan
malzeme tipine bağlıdır. Örneğin, havacılık veya uzay aracı parçalarında
aracın ağırlığını azaltmak için emniyet katsayısı 1’ e yakın seçilir. Nükleer güç
santralinde, malzeme davranışları veya yüklemedeki belirsizliklerden dolayı
bazı parçalar için emniyet katsayısı 3’ e kadar yüksek olabilir.
Birçok durumda, belirli bir durum için emniyet katsayısı veya emniyet
gerilmesi tasarım yönetmeliklerinde bulunur. Boyutlar böyle elde edilirse veya
emniyetli gerilme sınırı esas alınarak boyutlar belirlenmişse emniyetli tasarım
olarak adlandırılır. Bu metot, bir taraftan kamu ve çevre güvenliğini diğer
taraftan ekonomik değerlendirme dengesini birlikte sağlar.
Basit Bağlantılar
Malzeme davranışıyla ilgili basitleştirme kabullerinin yapılmasıyla =P/A
ve ort=V/A denklemleri basit bağlantı ve makine elemanlarının tasarım ve
boyutlarının belirlenmesinde sıklıkla kullanılır. Özellikle eleman kesiti
normal kuvvete maruz ise, kesitte ihtiyaç duyulan alan aşağıdaki ifadeden
belirlenir.
A=P /em
Diğer taraftan, eğer kesit ortalama kesme kuvvetine maruzsa, gerekli kesit
alan aşağıdaki ifadeden belirlenir.
A=P /em
Basit Bağlantılar
(yat)em
Düzgün kabul
edilen normal
gerilme dağılımı
A=P /(yat)em
B kolon kaidesi plakasının alanı betonun
emniyetli yatak gerilmesinden belirlenir.
Basit Bağlantılar
Beton içindeki çubuğun
gömülü l uzunluğu yapıştırıcı
bağın emniyetli kayma
dayanımı kullanılarak
belirlenir.
=
Düzgün kabul edilen kayma gerilme dağılımı
Basit Bağlantılar
Düzgün
kabul
edilen
kayma
gerilme
dağılımı
=
Basit Bağlantılar
Çelik ve ahşap bağlantılar tek kayma bağlantı örnek olarak gösterilmiştir.
Çelik ve ahşap bağlantılar çift kayma bağlantısına örnek olarak gösterilmiştir.
Kavramsal Çalışmalar
Yüksek topuklu ayakkabılar
yumuşak veya muşamba zemine
genellikle zarar verir.
Her bir topuğun altındaki yatak
gerilmesine dikkat ediniz.
Cıvatanın bu kırılma şekli tek
kesme hasarına örnektir.
Cıvatanın a-a kesiti gibi orta bir
yeri boyunca değil de plakalar
arasından kırılma oluşur.
Problemler
Problemler
Problemler
Problemler
Problemler
Problemler
Problemler