MERAKLISINA MATEMATİK
TRİGONOMETRİ
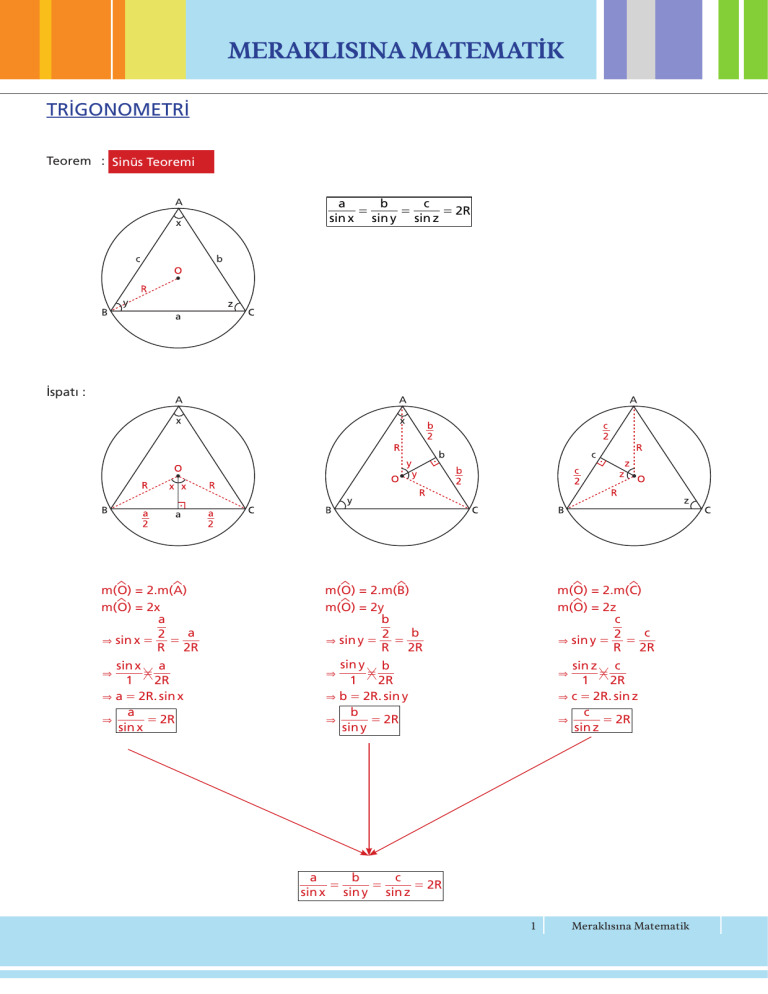
Teorem : Sinüs Teoremi
a
b
c
=
=
= 2R
sin x sin y sin z
İspatı :
m(ëO) = 2.m(ëA)
m(ëO) = 2x
a
a
2
& sin x = =
R 2R
sin x a
=
1
2R
& a = 2R. sin x
a
&
= 2R
sin x
&
m(ëO) = 2.m(ëB)
m(ëO) = 2y
b
b
2
& sin y = =
R 2R
sin y b
&
=
1
2R
& b = 2R. sin y
b
&
= 2R
sin y
m(ëO) = 2.m(ëC)
m(ëO) = 2z
c
c
2
& sin y = =
R 2R
sin z c
=
1
2R
& c = 2R. sin z
c
&
= 2R
sin z
&
a
b
c
=
=
= 2R
sin x sin y sin z
1
Meraklısına Matematik
MERAKLISINA MATEMATİK
Teorem : Kosinüs Teoremi
I. a2 = b2 + c2 - 2.b.c. cos a
II. b2 = a2 + c2 - 2.a.c. cos b
III. c2 = b2 + a2 - 2.b.c. cos i
İspatı :
I.
&
h2 + m2 = c2
m
2
2
2 . cos a = c
h + (b - m) = a
& h2 + m2 = c2 & h2 = c2 - m2 ifadesini
h2 – b2 – 2bm + m2 = a2 eşitliğinde yerine koyarsak
& c2 - m2 + b2 - 2bm + m2 = a2
m
& c2 + b2 - 2bm = a2 a c = cos a, m = cos a k
& c2 + b2 - 2.b. cos a = a2
II.
2
2
2
1) h + n = a
n
2
2
2 . cos b = a .n = a. cos b
2) h + ( c - n ) = b
(1) nolu denklemi (2) nolu denklemde yerine
yazacağız.
& h2 + n2 = a2
2
2
2
2
2
2
2
& h = c - n h + c - 2c.n + n = b
& a2 - n2 + c2 - 2c.n + n2 = b2
& a2 + c2 - 2c.n = b2 _n = a. cos bi
& a2 + c2 - 2.c.a. cos b = b2
1
&
A _ ABCi = .b.c. sin a
2
1
&
II) A _ ABCi = .a.c. sin b
2
1
&
III) A _ ABCi = .b.a. sin i
2
I)
Teorem :
2
Meraklısına Matematik
MERAKLISINA MATEMATİK
İspatı :
I.
&
A _ ABCi =
h .b
1
(1)
2
h
1
sin a = c & h = c. sin a (2)
1
(2) nolu denklemi (1) nolu denkelmde yerine
yazarsak;
II.
&
A _ ABCi =
h1.b
&
A _ ABCi =
h2 .c
2
2
=
c. sin a.b 1
= .c.b. sin a
2
2
(1)
h2
sin b = a & h = a. sin b (2)
2
(2) nolu denklemi (1) nolu denklemede yerine
yazarsak;
III.
&
A _ ABCi =
h2 .c
&
A _ ABCi =
h3 .a
2
2
=
a. sin b.c 1
= .a.c. sin b
2
2
(1)
h
sin a =
3
b
& h = b. sin b (2)
3
(2) nolu denklemi (1) nolu denklemede yerine
yazarsak;
&
A _ ABCi =
IIV.
h3 .a
2
=
b. sin a.a 1
= .b.a. sin i
2
2
2
2
2
k
& h = a - k ( 1)
cos i = a
h2 + _b - k i2 = c2 & h2 + b2 - 2bk + k2 = c2 (2) k = a. cos i
h2 + k2 = a2
(1) nolu denklemi (2) nolu denklemede yerine
yazarsak;
& a2 - k2 + b2 - 2bk + k2 = c2
& a2 + b2 - 2b.k = c2 _k = a. cos ii
& a2 + b2 - 2.b.a. cos i = c2
3
Meraklısına Matematik
MERAKLISINA MATEMATİK
İKİ YAYIN TOPLAM YADA FARKININ TRİGONOMETRİK ORANLARI
1.1. Teorem
a ve b herhangi iki reel sayı olmak üzere,
cos(a – b) = cosa.cosb + sina.sinb dir.
İspat :
a ve b reel sayıları ile a – b reel sayılarının birim çember
üzerindeki görüntüleri, B, C ve D olsun.
B(cosa, sina)
C(cosb, sinb)
D(cos(a – b), sin(a – b)
olduğunu, trigonometrik tamamından kolayca söyleriz.
Ayrıca, ölçüleri eşit olduğundan,
|BïC| = |AïD| yazılır. Öyleyse |BC| = |AD| dir. A noktasının A(1, 0) olduğunu biliyoruz. Analitik geometrideki
iki nokta arasındaki uzaklık förmülünü kullanarak,
BC =
AD =
_cos a - cos bi + _sin a - sin bi
2
2
2
8cos _a - bi - 1B + $sin _a - bi- 0A yazılır.
2
|BC|2 = |AD|2 yazılabildiğinden, her iki tarafın karesini alarak,
(cosa – cosb)2 + (sina – sinb)2 = [cos(a – b) – 1]2 + [sin(a – b) – 0]2 eşitliğinden
cos2a + cos2b – 2cosa. cosb + sin2a + sin2b – 2sina . sinb = cos2(a – b) + 1 – 2cos(a – b) + sin2(a – b) buluruz.
cos2a + sin2a = 1, cos2b + sin2b = 1 ve cos2(a – b) + sin2(a – b) = 1
eşitlikleri dikkate alınarak gerekli kısıtlamalar yapılırsa; cos(a – b) = cos.cosb + sina.sinb elde edilir.
1.2. Teorem
a ve b herhangi iki reel sayı olmak üzere,
cos(a + b) = cosa.cosb – sina.sinb dir.
İspat :
cos(a + b) = cos(a – (– b)) = cosa.cos( – b) + sina.sin( – b) olur.
Burada cos( – b) = cosb ve sin(– b) = – sinb olduğundan cos(a + b) = cosa.cosb – sina.sinb elde edilir.
4
Meraklısına Matematik
MERAKLISINA MATEMATİK
1.3. Teorem
sin(a – b) = sinb.cosb – sinb.cosa dır.
İspat :
r
r
r
r
sin _a - bi = cos ; - _a - biE = cos <b - al + bF = cos <b - al . cos b - sin b. sin b - alF
2
2
2
2
= sin a. cos b - sin b. cos a dır.
1.4. Teorem
a, b R için
sin(a + b) = sina.cosb + sinb.cosa dır.
İspat :
sin(a + b) = sin[a – (– b)] = sina. cos( – b) – sin(– b).cosa
cos( – b) = cosb ve sin(– b) = – sinb olduğundan, sin(a + b) = sina.cosb + sinb.cosa elde edilir.
1.5. Teorem
k Z olmak üzere, a !
tan _a + bi =
r
r
+ kr ve a + b ! + kr koşuluna uyan her a, b R için
2
2
tan a + tan b
dır.
1 - tan a. tan b
İspat :
tan _a + bi =
sin _a + bi
cos _a + bi
=
sin a. cos b + sin b. cos a
olur.
cos a. cos b - sin a. sin b
Pay ve paydayı cosa.cosb ile bölersek buradan, (cos.cosb ≠ 0)
sin a. cos b sin b. cos a
+
tan a + tan b
cos a. cos b cos b. cos a
tan _a + bi =
=
elde edilir.
cos a. cos b sin a. sin b
1 - tan a. tan b
cos a. cos b cos a. cos b
5
Meraklısına Matematik
MERAKLISINA MATEMATİK
1.6. Teorem
k Z omak üzere , a !
tan _a - bi =
r
r
r
+ kr, b ! + kr ve a - b ! + kr koşuluna uyan her a, b R için,
2
2
2
tan a - tan b
dir.
1 + tan a. tan b
İspat :
tan _a - bi = tan 8a + _- biB =
tan + tan _- bi
1 - tan . tan _- bi
=
tan a - tan b
olur.
1 + tan a. tan b
1.7. Teorem
k Z olmak üzere,
a ≠ k , b ≠ k , a + b ≠ k, a – b ≠ k koşuluna uyan her a, b R için
cot a. cot b - 1
cot a. cot b + 1
cot _a + bi =
ve cot _a - bi =
dır.
cot a + cot b
cot b - cot a
İspat :
cos a. cos b sin a. sin b
cos a.cob - sin a. sin b
cos a. cos b cos a. cos b
=
cot _a + bi =
=
sin a. cos b cos a. sin b
sin _a + bi sin a. cos b - cos a. sin b
+
cos a. cos b cos a. cos b
cos _a + bi
buradan cot _a + bi =
cot a. cot b - 1
elde edilir.
cot a + cob
cot(a – b) nin hesabı için yukarıdaki son frmülde (b) yerine (– b) yazarsak,
cot a. cot b + 1
cot _a - bi =
elde edilir.
cot b + coa
DÖNÜŞÜM VE TERS DÖNÜŞÜM FORMÜLLERİ
1. DÖNÜŞÜM FÖRMÜLLERİ
1.8. Teorem
x ve y herhangi iki reel sayı olmak üzere,
x+y
x-y
. cos
2
2
x+y
x-y
cos x + cos y = 2 sin
. cos
2
2
sin _ x + y i
tan x + tan y = cos x. cos y
sin x + sin y = 2 sin
cot x + cot y =
sin _ x + y i
sin x. sin y
,
x-y
x+y
. cos
2
2
x+y
x-y
cos x - cos y = - 2 sin
. sin
2
2
sin _ x - y i
tan x - tan y = cos x. cos y
,
cot x - cot y =
sin x - sin y = 2 sin
,
,
sin _ y - x i
sin x. sin y
dır.
6
Meraklısına Matematik
MERAKLISINA MATEMATİK
İspat :
sin (a + b) = sin a. cos b + sin b. cos a
4
sin (a - b) = sin a. cos b - sin b. cos a
taraf tarafa toplanırsa
sin (a + b) + sin (a - b) = 2 sin a. cos b..... (1)
bulunur
+
x+y
x-y
, b=
olur.
2
2
a + b = x ve a - b = y denirse, a =
Öyleyse, sin x + sin y = 2 sin
x+y
x-y
dir.
. cos
2
2
y yerine – y alınırsa, sin x + sin y = 2 sin
x-y
x+y
elde edilir.
. cos
2
2
Benzer şekilde,
cos (a + b) = cos a. cos b - sin a. sin b
4
sin (a - b) = cos a. cos b + sin a. sin b
taraf tarafa toplanırsa
cos (a + b) + cos (a - b) = 2 cos a. cos b.... (1)
bulunur
+
a + b = x ve a - b = y denirse, a =
cos x + cos y = 2 cos
x+y
x-y
değeri yerine konulursa
,b =
2
2
x+y
x-y
olur.
. cos
2
2
verilen eşitlikleri taraf tarafa çıkarırsak, cos(a + b) – cos(a – b) = – 2sina.sinb .........(2) elde edilir ve
cos x - cos y = - 2 sin
x+y
x-y
olur.
. sin
2
2
sin _ x + y i
sin x sin y sin x. cos y + cos x. sin y
tan x + tan y = cos x + cos y =
= cos x. cos y olur.
cos x. cos y
sin _ x - y i
Burada y yerine – y konursa, tan x - tan y = cos x. cos y elde edilir.
Aynı şekilde, cot x + cot y =
cos x cos y sin y. cos x + sin x. cos y sin _ y + x i
+
=
=
bulunur.
sin x sin y
sin x. sin y
sin x. sin y
y yerine – y konursa, cot x - cot y =
sin _- y + x i
sin x. sin _- y i
=
sin _ y - x i
elde edilir.
sin x. sin y
7
Meraklısına Matematik
MERAKLISINA MATEMATİK
2.
TERS DÖNÜŞÜM FÖRMÜLLERİ
1.9. Teorem
p ve q herhangi iki reel sayı olmak üzere,
1
sin q. cos q = 8sin _p + qi + sin _p - qiB
2
1
cos p. cos q = 8cos _p + qi + cos _p - qiB
2
1
1
sin p. sin q = - 8cos _p + qi - cos _p - qiB = 8cos _p - qi - cos _p + qiB dür.
2
2
İspat :
sin (p + q) = sin p. cos q + sin q. cos p
4
sin (p - q) = sin p. cos q - sin q. cos p
taraf tarafa toplanırsa
+
sin (p + q) + sin (p - q) = 2 sin p. cos q yada
1
sin p. cos q = 7sin (p + q) + sin (p - q)A
2
olur
Aynı şekilde;
cos (p + q) + cos (p - q) = 2 cos p. cos q
4
sin p (p - q) cos p. cos q + sin p. sin q
taraf tarafa toplanırsa
+
cos (p + q) + cos (p - q) = 2 cos p. cos q yada
1
cos p. cos q = 7cos (p + q) + cos (p - q)A
2
bulunur
Verilen şekilleri tarat tarafa çıkarırsak,
cos (p + q) - cos (p - q) = - 2 sin p. sin q
1
sin .siq = - 7cos (p + q) - cos (p - q)A
2
yada
elde edilir.
8
Meraklısına Matematik
MERAKLISINA MATEMATİK
3.
YARIM AÇI FÖRMÜLLERİ
Bir reel sayının trigonometrik görüntüsünü bu sayının yarısının trigonometrik görüntüleri türünden veren
formüller, uygulamada oldukça büyük kolaylık sağlar. Yarım açı formülleri denilen bu formülleri kolayca
elde edebiliriz.
Teorem
cos 2a = cos2 a - sin 2a = 2 cos2 a - 1 = 1 - 2 sin2 a
İspat : cos2a = cos(a + a) cos 2a = cos2 a - sin2 a = cosa.cosa - sina.sina bulunur.
sin2a = 1 - cos2a ve cos2a = 1 - sin2a yazılarak cos 2a = 2 cos 2a - 1 ve cos 2a = 1 - 2 sin2 a förmülleri
elde edilir. Bunlar gibi;
Teorem
sin2 = 2sin . cos
İspat : sin2a = sin(a + a) , sin2a = sina.cosa + sina.cosa sin 2a = 2 sin a. cos a bulur.
Aynı şekilde,
Teorem
tan 2a =
2 tan a
2
1 - tan a
İspat : tan2a = tan(a + a) , tan 2a =
2 tan a
tan a + tan a
, tan 2a =
elde edilir.
2
1 - tan a. tan a
1 - tan a
Benzer yolla,
Teorem
2
cot 2a =
cot a
2 cot a
İspat : cot1a = cot(a + a) , cot 2a =
cot a. cot a - 1
cot2 a - 1
, cot 2a =
elde edilir.
cot a + cot a
2 cot a
9
Meraklısına Matematik
MERAKLISINA MATEMATİK
TÜREV ALMA KURALLARI
Teorem
f(x) = a (a R) ise f(x) = 0
İspat : fl (x) = lim
h"0
f (x + h) - f (x)
a-a
= lim
& fl (x) = 0
h
"
0
h
h
Teorem
f(x) = a.x ise f(x) = a
İspat : fl (x) = lim
h"0
f (x + h) - f (x)
a ( x + h ) - a .x
a.h
= fl (x) & lim
= lim
& fl (x) = a
h
"
0
h
"
0
h
h
h
Teorem
f(x) = axn (n N+) ise f(x) = n.a.xn–1
n
n
n
n
f (x + h) - f (x)
a (x + h) - ax
(x + h) - x
& fl (x) = lim
& fl (x) = a. lim
h"0
h
"
0
h
"
0
h
h
h
İspat : fl (x) = lim
& fl (x) = a. lim
(x + h - x) 8(x + h)
n-1
+ ...B
h
h"0
& fl (x) = a. lim 8(x + h) n
-1
h"0
+ (x + h) n
-2
.x + ( x + h ) n
-3
.x2 + ... + xn 1B
& fl (x) = a.n.xn - 1
Teorem
1
f l ( x) = x
ise fl (x) = -
1
x2
x - (x + h)
1
1
-x
x (x + h)
-h
-1
-1
x+h
İspat : fl (x) = lim
= lim
& fl (x) = lim
= lim
& fl (x) = 2
h"0
h
"
0
h " 0 hx (x + h)
h " 0 x (x + h)
x
h
h
Teorem
f l ( x) =
x
ise f (x) =
İspat : fl (x) = lim
h"0
1
2 x
( x+h - x).( x+h + x)
x+h - x
& fl (x) = lim
h"0
h
h. ( x + h + x )
& fl (x) = lim
h " 0 h. (
x+h-x
x+h + x)
= lim
h"0
1
x+h + x
& fl (x) =
1
2 x
10
Meraklısına Matematik
MERAKLISINA MATEMATİK
Teorem
f (x) = f (x) + g (x) ise fl (x) + gl (x)
İspat : fl (x) = lim
7f (x + h) + g (x + h)A - 7f (x) + g (x)A
h
h"0
& fl (x) = lim
h"0
& fl (x) lim
h"0
f (x + h) - f (x) + g (x + h) - g (x)
h
g (x + h) - g (x)
f ( x + h ) - f ( x)
+ lim
& fl (x) = fl (x) + gl (x)
h
"
0
h
h
Teorem
f (x) = f (x) .g (x) ise fl (x) = fl (x) .g (x) + f (x) .gl (x)
İspat : fl (x) = lim
7f (x + h) .g (x + h)A - 7f (x) .g (x)A
h
h"0
& fl (x) = lim
h"0
Teorem
f ( x)
f ( x) =
g ( x)
& fl (x) lim =
h"0
f (x + h) .g (x) + f (x) .g (x) f (x + h) .g (x) - f (x + h) .g (x)
G
+
h
h
g (x + h) - g (x)
f (x + h) - f (x)
.g (x) + lim f (x + h) .
& fl (x) = fl (x) .g (x) + f (x) .gl (x)
h"0
h
h
ise fl (x) =
fl (x) .g (x) - f (x) .gl (x)
g2 (x)
f (x + h) f (x)
g (x + h) g (x)
f (x + h) .g (x) - f (x) .g (x + h)
l
İspat : f (x) = lim
& fl (x) = lim
h"0
h"0
h
h . g ( x + h ) . g ( x)
& fl (x) = lim >
h"0
f (x + h) .g (x) - f (x) .g (x + h) f (x) .g (x) - f (x) .g (x)
+
H
h.g (x + h) .g (x)
h . g ( x + h ) . g ( x)
& fl (x) = lim *
h"0
& fl (x) = lim =
h"0
7f (x + h) - f (x) .g (x)A
h.g (x + h) .g (x)
-
f (x) . 7g (x + h) - g (x)A
h.g (x + h) .g (x)
4
g (x + h) - g (x)
fl (x) .g (x) - f (x) .gl (x)
f ( x + h ) - f ( x)
1
G . lim
.g (x) - f (x) .
& f l ( x) =
2
h
"
0
h
h
g ( x + h ) . g ( x)
7g (x)A
Teorem
f (x) =
1
g (x)
ise fl (x) = -
gl (x)
7g (x)A
2
1
1
g (x + h) g (x)
g (x + h) - g (x)
İspat : fl (x) = lim
& fl (x) = lim >
H
h"0
h " 0 h.g (x + h) .g (x)
h
& fl (x) = - lim
1
h " 0 g (x + h) .g (x)
.
g (x + h) - g (x)
- gl (x)
-1
& fl (x) =
.gl (x) & fl (x) =
2
h
7g (x)A
7g (x)A
11
Meraklısına Matematik
MERAKLISINA MATEMATİK
Teorem
1
f (x) = ln x ise fl (x) = x
1
ln (x + h) - ln (x)
1
x+h
h h
& fl (x) = lim . ln b x l = limln b1 + x lh x = t tanımını kullanacağız.
h"0
h " 0h
h"0
h
g (x + h) - g (x)
f ( x + h ) - f ( x)
& fl (x) = lim
+ lim
& fl (x) = fl (x) + gl (x) diyelim.
h"0
h
"
0
h
h
İspat : fl (x) = lim
1
1 1 1
1
1
= . x ve h " 0 iken t " 0 olur. & fl (x) = ln e h = x . ln e & fl (x) = x
t
h
Teorem
f (x) = ex ise
f l ( x) = e x
x
x
h
h
x
e + h - e ( e - 1)
-e
e -1 h
x
= lim
& fl (x) = e . lim
e - 1 = t diyelim.
h"0 h
h"0
h"0
h
h
h = ln (t + 1) ve h " 0 iken t " 0 olur.
t
1
1
& fl (x) = ex . lim
& fl (x) = ex . lim
& fl (x) = ex = lim
1
t " 0 ln (t + 1)
t"0 1
t"0
t
. ln (t + 1)
ln
(
t
+
1
)
t
İspat : fl (x) = lim
e
x+h
& fl (x) = ex . lim
1
t " 0 ln e
& fl (x) = ex
Teorem
f (x) = ax ise
fl (x) = ax .ha
x
h
h
x
a ( a - 1)
-a
a -1 h
x
= lim
& fl (x) = a . lim
a - 1 = t diyelim.
h"0 h
h"0
h"0
h
h
h = loga (t + 1) ve h " 0 iken t " 0 olur.
İspat : fl (x) = lim
a
x+h
& fl (x) = ax . lim
t " 0 log
& fl (x) = ax .
t
1
1
x
& fl (x) = ax . lim
& fl (x) = a . lim
1
0
t
0
t
"
"
1
( t + 1)
h
a
. loga (t + 1)
log
a
lim
(
t
+
1
)
t
t"0
1
& fl (x) = ax . ln a
loga e
Teorem
f (x) = sin x ise fl (x) = cos x
İspat : fl (x) = lim
h"0
sin (x + h) - sin (x)
& fl (x) = lim
h"0
h
sin
& fl (x) = lim
h
2
h
1 44 2244 3
h"0
2 sin d
x+h-x
x+h+x
n . cos d
n
2
2
h
h
. limcos d x n & fl (x) = cos x
h"0
2
1
12
Meraklısına Matematik
MERAKLISINA MATEMATİK
Teorem
f (x) = cos x ise fl (x) = - sin x
cos (x + h) - cos (x)
& fl (x) = lim
İspat : fl (x) = lim
h"0
h"0
h
sin
& fl (x) = lim
h
2
h
1 44 2244 3
h"0
- 2 sin d
x+h-x
x+h+x
h
h
2 sin . sin d x + n
n . sin d
n
2
2
2
2
& fl (x) = lim
h"0
h
h
h
. lim =- sin d x + nG & fl (x) = - sin x
h"0
2
1
Teorem
f (x) = tan x ise fl (x) = 1 + tan2 x
İspat : fl (x) = lim
h"0
& f l ( x) =
tan (x + h) - tan (x)
sin (x + h - x)
sin (x + h - x)
& fl (x) = lim
& fl (x) = lim
h " 0 cos (x + h) . cos x
h " 0 cos (x + h) . cos x
h
1
2
cos x
;
veya & fl (x) =
cos2 x + sin2 x
2
cos x
& fl (x) = 1 + tan2 x
Teorem
f (x) = fog (x) = f (g (x)) ise fl (x) = f (g (x)) .gl (x)
İspat : fl (x) = lim
h"0
f (g (x + h) - f (g (x))
g (x + h) - g (x) = k diyelim.
h
g(x + h) = g(x) + k ve h 0 iken k 0 olur.
& fl (x) = lim =
h"0
f (g (x) + k) - f (g (x)) k
. G
k
h
İlk çarpanda g(x) = u koyalım. Bunu, görmeyi kolaylaştırması için yapıyoruz.
g (x + h) - g (x)
f ( u + k) - f ( u )
& fl (x) = lim
. lim
. & fl (x) = fl (u) .gl (x) & fl (x) = fl (g (x)) .gl (x)
k"0
h"0
k
h
1 4444 2 4444 3
f l ( u)
Bu son formül. “Zincir Kuralı” adıyla şöyle de ifade edilir : z = f(u) , u = g(x) ve x’in x artmasına karşılık
u ve z fonksiyonlarındaki artmalar u ve z olsun.
Tz Tz Tu
Tz
Tz Tu
=
.
& lim
= lim d
.
n
Tx Tu Tx Tx " 0 Tx Tx " 0 Tu Tx
u ve z türevleri var olan fonksiyonlar olarak kabul edilirse, x 0 iken u 0 olur.
& lim =
4x " 0
Tz
Tz Tu
Tz
Tz
Tu
dz dz du
= lim d
.
= lim d
. lim
=
.
n & lim =
n&
4x " 0 Tx
Tx " 0 Tu 4x " 0 Tx
Tx 4x " 0 Tu Tx
dx du dx
13
Meraklısına Matematik
MERAKLISINA MATEMATİK
Teorem
g (x) = f-1(x) = y ise gl (x) =
1
fl (y)
-1
İspat : f (x) = g (x) & fog (x) = x & f (g (x)) = x
f (g (x)) = x & fl (g (x)) .gl (x) = 1 & gl (x) =
dy
1
1
&
=
fl (g (x)) dx dx
dy
-1
Bu sonucu şöyle ifade edebiliriz. & (f )l (x) =
1
fl (y))
Teorem
ise fl (X) =
f (x) = arcsin x = y
1
1 - x2
x
x
h
h
x
e + h - e ( e - 1)
-e
e -1 h
x
= lim
& fl (x) = e . lim
e - 1 = t diyelim.
h"0 h
h"0
h"0
h
h
h = ln (t + 1) ve h " 0 iken t " 0 olur.
t
1
1
& fl (x) = ex . lim
& fl (x) = ex . lim
& fl (x) = ex = lim
1
t " 0 ln (t + 1)
t"0 1
t"0
t
. ln (t + 1)
ln
(
t
+
1
)
t
İspat : fl (x) = lim
e
x+h
& fl (x) = ex . lim
1
t " 0 ln e
& fl (x) = ex
Teorem
f (x) = ax ise
fl (x) = ax .ha
İspat : y = arcsinx x = siny zincir kuralı işimizi çok kolaylaştırır.
x = sin y & 1 =
d (sin y) dy dy
1
&
= fl (x) = cos y & fl (x) =
.
dy
dx dx
1
1 - sin2 y
& fl (x) =
1
1 - x2
Aynı Şekilde;
f (x) = arccos x & fl (x) =
f (x) = arctan x & fl (x) =
f (x) = arc cot x & fl (x) =
-1
1 - x2
-1
1 + x2
-1
1 + x2
bulunur. Ters fonksiyonların türevleri doğrudan doğruya türev tanımıyla da bulunabilir. Ancak bu oldukça
işlemi bol bir yoldur. Buraya kadar her bilgiyi öncekinin üzerine koyarak geldiğimize göre, elde ettiğimiz
bilgileri işimizi kolaylaştırmak için kullanmalıyız.
14
Meraklısına Matematik
MERAKLISINA MATEMATİK
Teorem
1
f (x) = m x = y (m ! Z+) ise fl (x) =
m.
İspat :
m
m
m-1
x
d (ym) dy
dy
1
x =y&x=y &1=
.
& 1 = mym - 1.
=
dy dx
dx mym - 1
m
Burada, ym–1 değerini x türünden bulalım.
x
x
m
ym = x & ym - 1 = y = m = xm - 1
x
dy
dy
1
1
1
=
&
=
& f ( x) =
m m-1
dx mym - 1 dx m. m xm - 1
m. x
Teorem
f (x) = ef (x) ise fl (x) = ef (x) .fl (x)
İspat : f(x) , bileşke fonksiyonun türevini alma kuralı ile, f(x) = ef(x) . f(x) olarak bulunur. Biz bunu bir de türev
tanımı ile bulalım:
fl (x) = lim
e
f ( x + h)
e
f (x) + k
h"0
fl (x) = lim
h"0
-e
h
f ( x)
-e
h
, f(x + h) - f(x) = k diyelim. f(x+ h) = f(x) + k ve h 0 iken k 0 olur.
f (x)
k
k
e -1
e -1 k
& fl (x) = ef (x) . lim e
. o
h"0 h
h"0
h h
& fl (x) = ef (x) . lim
k
f (x + h) - f (x)
e -1
f x
. lim
& fl (x) = e ( ) .fl (x)
k"0 k
h"0
h
1 4444 2 4444 3
& fl (x) = ef (x) . lim
f l ( x)
15
Meraklısına Matematik








