mb1001 analiz ı - İstanbul Kültür Üniversitesi

MB1001 ANALİZ I
Ders Notları
Yrd. Doç. Dr. Emel YAVUZ DUMAN
İstanbul Kültür Üniversitesi
Matematik-Bilgisayar Bölümü
c 2013, Emel Yavuz Duman
Tüm hakkı saklıdır.
Bu notlar Örgün Öğretimde Uzaktan Öğretim Desteği (UDES) lisansı altındadır. Ders notlarına ulaşmak için http://udes.iku.edu.tr/ internet adresine bakınız.
İlk yayınlanma: 2013, Eylül
Yavuz Duman, Emel
İstanbul Kültür Üniversitesi
Fen-Edebiyat Fakültesi
Matematik-Bilgisayar Bölümü
MB1001 Analiz I
Ders Notları
Ataköy Kampüs
34156, Bakırköy
İstanbul - Turkey
e.yavuz@iku.edu.tr
http://web.iku.edu.tr/∼eyavuz/
İçindekiler
İçindekiler
1 Reel (Gerçel) Sayı Sistemi
1.1 Temel Tanımlar . . . . . . . . . .
1.2 Sıralanmış Cisim Aksiyomları . .
1.3 Tamlık Aksiyomu . . . . . . . . .
1.4 Ters Fonksiyonlar ve Görüntüler
iii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
4
18
26
2 Reel Değerli Diziler
2.1 Dizilerin Limitleri . . . . . . . . . .
2.2 Limit Teoremleri . . . . . . . . . .
2.3 Bolzano-Weierstrass Teoremi . . .
2.4 Cauchy Dizileri . . . . . . . . . . .
2.5 Limit Supremum ve Limit İnﬁmum
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
35
35
41
48
54
59
3 R Üzerinde Fonksiyonlar
3.1 İki-Yönlü Limitler . . . . . . . . . . . . . . . .
3.2 Tek-Yönlü Limitler ve Sonsuzda Limit Kavramı
3.3 Süreklilik . . . . . . . . . . . . . . . . . . . . .
3.4 Düzgün Süreklilik . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
67
67
76
83
92
4 R Üzerinde Diferansiyellenebilme
4.1 Türev . . . . . . . . . . . . . . . . . . . . . . .
4.2 Diferansiyellenebilme Teoremleri . . . . . . . .
4.3 Bazı Fonksiyonların Türevleri . . . . . . . . . .
Trigonometrik Fonksiyonların Türevleri . . . .
Kapalı Fonksiyonların Türevleri . . . . . . . . .
Ters Trigonometrik Fonksiyonların Türevleri . .
Logaritmik ve Üstel Fonksiyonların Türevleri .
4.4 Ortalama Değer Teoremi . . . . . . . . . . . . .
4.5 Limitlerde Belirsiz Şekiller ve L’Hôpital Kuralı
0\0 Belirsizliği . . . . . . . . . . . . . . . . . .
∞\∞, ∞ · 0, ∞ − ∞ Belirsizlikleri . . . . . . .
Belirsiz Kuvvetler . . . . . . . . . . . . . . . . .
4.6 Fonksiyon Graﬁklerinin Çizimi . . . . . . . . .
4.7 Ters Fonksiyon Teoremleri . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
99
99
108
111
111
114
116
117
120
125
126
127
128
130
134
1 Reel (Gerçel) Sayı Sistemi
1.1
Temel Tanımlar
Bu derste küme ve reel sayılar için standart notasyonlar kullanılacaktır. Örneğin, R veya (−∞, ∞) reel sayılar kümesini, ∅ ise boş kümeyi (hiç bir elemanı olmayan küme) temsil edecektir. a ∈ A notasyonu a’nın A kümesinin
bir elemanı olduğunu, a ∈
/ A ise elemanı olmadığını söyler. Verilen bir sonlu
kümeyi iki farklı şekilde ifade edebiliriz. Elemanları açık olarak listeleyebilir
veya kümeyi cümleler veya denklemler ile tanımlayabiliriz. Örneğin, x2 = 1
denkleminin çözümleri kümesi
{−1, 1} veya {x : x2 = 1}
şeklinde gösterilebilir.
A ve B iki küme olsun. A’nın B kümesinin bir alt kümesi (notasyon: A ⊆
B) olabilmesi olarak isimlendirilmesi için gerek ve yeter şart A kümesinin her
elemanının aynı zamanda B kümesine de ait olmasıdır. Eğer A kümesi B’nin
bir alt kümesi, fakat B kümesinin A’ya ait olmayan en az bir b ∈ B elemanı
var ise bu durumda A’ya B’nin özalt kümesi (notasyon: A ⊂ B) denir. A ve B
kümelerinin eşit (notasyon: A = B) olarak adlandırılması için gerek ve yeter
şart A ⊆ B ve B ⊆ A içermelerinin sağlanmasıdır. Eğer A ve B eşit değil ise
A 6= B yazılır. Bir A kümesinin boştan farklı olarak isimlendirilmesi için gerek
ve yeter şart A 6= ∅ olmasıdır.
A kümesine veya B kümesine veya her iki kümeye de ait x elemanlarının
oluşturduğu kümeye A ile B’nin birleşimi (notasyon: A ∪ B) denir ve
A ∪ B = {x : x ∈ A veya x ∈ B}
olarak gösterilir. Hem A hem de B kümesine ait x elemanlarının oluşturduğu
kümeye A ile B’nin kesişimi (notasyon: A ∩ B) adı verilir ve
A ∩ B = {x : x ∈ A ve x ∈ B}
şeklinde ifade edilir. A kümesine ait fakat B kümesine ait olmayan x elemanlarının kümesine B’nin A’ya göre tümleyeni (notasyon: A\B veya A’nın anlaşılması durumunda B c ) denir ve
A\B = {x : x ∈ A, x ∈
/ B}
olarak gösterilir. Örneğin,
{−1, 0, 1} ∪ {1, 2} = {−1, 0, 1, 2},
{1, 2}\{−1, 0, 1} = {2},
{−1, 0, 1} ∩ {1, 2} = {1},
{−1, 0, 1}\{1, 2} = {−1, 0}.
X ve Y iki küme olsun. X ve Y ’nin Kartezyen çarpımı
X × Y := {(x, y) : x ∈ X, y ∈ Y }
şeklinde tanımlanan sıralı ikililerin kümesidir (:= sembolünün anlamı tanıma
göre eşit veya olarak tanımlansındır). (x, y), (z, w) ∈ X × Y gibi iki noktanın
eşit olarak adlandırılması için gerek ve yeter şart x = z ve y = w ifadelerinin
gerçeklenmesidir. Örneğin X = {1, 2, 3} ve Y = {1, 5} ise X × Y , elemanları
(1, 1), (1, 5), (2, 1), (2, 5), (3, 1), (3, 5)
olan sıralı ikililerin kümesidir.
X ve Y iki küme olsun. X ×Y ’nin herhangi bir alt kümesine X ×Y üzerinde
bir bağıntı adı verilir. X × Y üzerinde bir bağıntı R olsun. R’nin tanım kümesi
{x ∈ X : (x, y) ∈ R olacak şekilde y ∈ Y vardır}
ve R’nin değer kümesi
{y ∈ Y : (x, y) ∈ R olacak şekilde x ∈ X vardır}
olarak tanımlanır. (x, y) ∈ R olması durumunda genellikle xRy yazılır.
X ve Y iki küme, f ise X ×Y üzerinde bir bağıntı olsun. Eğer her bir x ∈ X
için (x, y) ∈ f olacak şekilde bir ve yalnız bir y ∈ Y var ise f ’ye X kümesinden
f
Y kümesine bir fonksiyon (notasyon: f : X → Y veya X → Y ) denir. Buna
göre X × Y üzerinde tanımlı bir bağıntının fonksiyon olabilmesi için her x ∈ X
için (x, y) ∈ f olacak şekilde bir y ∈ Y olmalı ve ayrıca (x, y) ∈ f ve (x, y ′ ) ∈ f
ise y = y ′ eşitliği sağlanmalıdır. f : X → Y bir fonksiyon ise X kümesine f ’in
tanım kümesi (notasyon: Dom(f ) := X) adı verilir.
Açık olarak, X kümesinin her x elemanına f fonksiyonu ile bir y = f (x) ∈ Y
tekabül eder. (x, y) ∈ f ise y’ye x’in f altındaki görüntüsü (veya değeri veya
resmi ) (notasyon: y = f (x) veya f : x 7→ y), x’e y’nin f altındaki ön görüntüsü
(veya orijinali ) denir. Fonksiyon tanımından da anlaşılacağı üzere ön görüntü
tek türlü belirli olmak zorunda değildir. Örneğin, her k = 0, ±1, ±2, · · · için
f (x) = sin(kπ) = 0 sağlanmakla birlikte 0 değerinin f (x) = sin x fonksiyonu
altında sonsuz sayıda ön görüntüsü vardır.
f fonksiyonu X’den Y ’ye bir fonksiyon olsun. Bu durumda f fonksiyonu
X üzerinde tanımlanmıştır denir ve Y kümesine eş-tanım kümesi adı verilir. f
fonksiyonunun değer kümesi
Ran(f ) := {y ∈ Y : f (x) = y olacak şekilde x ∈ X vardır}
şeklinde tanımlanan f ’in tüm görüntülerinin bir koleksiyonudur.
2
f
.x
. y = f (x)
Ran(f )
X = Dom(f )
Y eş-tanım kümesi
Genel halde, bir fonksiyonun değer kümesi, eş-tanım kümesinin bir alt kümesidir ve her y ∈ Ran(f ) elemanı bir veya birden fazla ön görüntüye sahiptir.
Eğer Ran(f ) = Y ve her y ∈ Y elemanı f altında sadece bir tane x ∈ X ön
görüntüsüne sahip ise bu durumda f : X → Y fonksiyonunun bir tersi vardır
denir ve ters fonksiyon f −1 (y) := x olmak üzere f −1 : Y → X şeklinde tanımlanır, burada x ∈ X için f (x) = y dir. Eğer f : X → Y fonksiyonunun tersi var
ise her x ∈ X ve y ∈ Y için
f −1 (f (x)) = x ve f (f −1 (y)) = y
sağlanır.
f ve g gibi iki fonksiyonun eşit olması için gerek ve yeter şart her iki
fonksiyonun da aynı tanım kümesine ve aynı değerlere sahip olmasıdır. Yani,
f, g : X → Y fonksiyonları her x ∈ X için f (x) = g(x) eşitliğini sağlar ise
eşittirler. Eğer iki fonksiyonun tanım kümeleri farklı ise fonksiyonlar farklıdır.
Örneğin, f (x) = g(x) = x2 olsun. Eğer f : [0, 1) → [0, 1) ve g : (−1, 1) → [0, 1)
ise f ve g iki farklı fonksiyondur. Her iki fonksiyonun da değer kümesi [0, 1)
√
olmakla birlikte, her y ∈ (0, 1)’nin f altında y şeklinde tek türlü belirli bir ön
√
görüntüsü mevcutken, g altında ±√ y şeklinde iki farklı ön görüntüsü vardır.
Buna göre f fonksiyonu f −1 (x) = x ters fonksiyonuna sahip olmakla birlikte
g’nin ters fonksiyonu yoktur.
X ve Y iki küme olsun. f : X → Y fonksiyonu x1 , x2 ∈ X olmak üzere x1 6=
x2 iken f (x1 ) 6= f (x2 ) özelliğini sağlıyor ise injektif (veya bire-bir veya bire-bir
içine) olarak adlandırılır. Fonksiyon tanımından ötürü her elemanın görüntüsü
tek türlü belirlidir. Yani her fonksiyon için f (x1 ) 6= f (x2 ) ise x1 6= x2 olmak
zorundadır. Eğer f (x1 ) 6= f (x2 ) iken x1 = x2 = x olsaydı, bu x elemanının
f (x1 ) ve f (x2 ) gibi iki farklı görüntüsü olurdu ki bu ise f ’in fonksiyon olma
tanımı ile çelişirdir. Eğer f fonksiyonu injektif ise x1 6= x2 iken f (x1 ) 6= f (x2 )
olacağından injektif bir fonksiyon için f (X) kümesinin her elemanının ancak
tek bir ön görüntüsü olabilir. Şu halde injektif bir fonksiyon için f (x1 ) = f (x2 )
ise x1 = x2 eşitliği sağlanır. Örneğin, f : R → R olmak üzere f (x) = x2
şeklinde tanımlanan fonksiyon −1 6= 1 iken f (−1) = f (1) = 1 olduğundan
injektif değildir. Diğer taraftan g : R → R olmak üzere g(x) = x + 1 fonksiyonu
3
x1 6= x2 için x1 + 1 6= x2 + 1 yani g(x1 ) 6= g(x2 ) ifadesini sağladığından
injektiftir.
X ve Y iki küme ve f : X → Y bir fonksiyon olsun. Eğer f (X) = Y eşitliği
sağlanıyor, yani Ran(f ) = Y ise f fonksiyonu sürjektif (veya üzerine veya
örten) olarak adlandırılır. Buna göre herhangi bir y ∈ Y için f (x) = y olacak
şekilde en az bir x ∈ X vardır. Örneğin, f : R → R olmak üzere f (x) = x2
şeklinde tanımlanan fonksiyon sürjektif değildir. Çünkü, hiç bir negatif sayı f ’in
görüntüsünde yer almaz. Bununla beraber g : R → R olmak üzere g(x) = x + 1
fonksiyonu, verilen her y sayısı için y = g(y − 1) şeklinde yazılabileceğinden
sürjektiftir.
Hem injektif hem de sürjektif olan bir f : X → Y fonksiyonuna bijektif
adı verilir. Buna göre her y ∈ Y için f (x) = y eşitliğini sağlayan tek türlü
belirli bir x ∈ X vardır (varlığı f ’in sürjektif olması, tekliği ise injektif olması
garantiler). Örneğin, X = {x ∈ R : x 6= 1} olmak üzere her x ∈ X için f (x) =
2x
x−1 şeklinde tanımlansın. f ’in injektif olduğunu göstermek için f (x1 ) = f (x2 )
eşitliğini sağlayan x1 , x2 ∈ X noktalarını göz önüne alalım. f (x1 ) = f (x2 )
olduğundan
2x2
2x1
=
x1 − 1
x2 − 1
eşitliği sağlanır. Bu ise x1 (x2 − 1) = x2 (x1 − 1) yani x1 = x2 demektir. Dolayısıyla f injektiftir.
Sürjektiﬂiği garantilemek için f ’in değer kümesini belirleyelim. Bunun için
y
2x
x’e bağlı verilen y = x−1
denklemini y cinsinden yazarsak x = y−2
elde edilir
ki bu ifade y 6= 2 için tanımlıdır. Buna göre f ’in değer kümesi Y := {y ∈ R :
y 6= 2} için yukarıdaki şekilde tanımlanan fonksiyon sürjektiftir. Dolayısıyla
f fonksiyonu X’den Y ’ye bir bijeksiyondur. f bir bijeksiyon olduğundan f ’in
x
tersi f −1 : Y → X fonksiyonu f −1 (x) = x−2
şeklinde tanımlıdır.
1.2
Sıralanmış Cisim Aksiyomları
Bu kısımda reel sayı sisteminin cebirsel yapısı üzerde durulacaktır. Reel sayılar
kümesinin her eleman çifti için aşağıdaki özellikleri sağlayan toplama ve çarpma
işlemleri bu küme üzerinde komütatif cisim (veya kısaca cisim) adı verilen bir
cebirsel yapı belirtirler.
Postulat 1 [Cisim Aksiyomları]. R2 := R × R üzerinde tanımlanmış ve her
a, b, c ∈ R için aşağıdaki özellikleri sağlayan “+” ve “·” fonksiyonları vardır:
Kapalılık Özelliği. a + b ∈ R ve a · b ∈ R dir.
Asosyatiﬂik (Birleşme) Özelliği. a+(b+c) = (a+b)+c ve a·(b·c) = (a·b)·c
dir.
Komütatiﬂik (Değişme) Özelliği. a + b = b + a ve a · b = b · a dır.
Distribütiﬂik (Dağılma) Özelliği. a · (b + c) = a · b + a · c dır.
Toplamanın Etkisiz Elemanının Varlığı. Her a ∈ R için 0 + a = a olacak
şekilde tek türlü belirli bir 0 ∈ R vardır.
Çarpmanın Birim Elemanının Varlığı. Her a ∈ R için 1 · a = a ve 1 6= 0
olacak şekilde tek türlü belirli bir 1 ∈ R vardır.
4
Toplamada Ters Elemanların Varlığı. Her x ∈ R için x + (−x) = 0 olacak
şekilde tek türlü belirli bir −x ∈ R vardır.
Çarpmada Ters Elemanların Varlığı. Her x ∈ R\{0} için x · (x−1 ) = 1
olacak şekilde tek türlü belirli bir x−1 ∈ R vardır.
Buna göre toplama ve çarpma işlemleri, R reel sayılar kümesi üzerinde bir
komütatif cisim yapısı belirtirler.
Genellikle a + (−b) ifadesi a − b, a · b ifadesi ab, a−1 ifadesi a1 veya 1/a
ve a · b−1 ifadesi ab veya a/b şeklinde gösterilir. Toplamada ve çarpmada ters
elemanların varlığının garantisi ile her a ∈ R için x + a = 0 ve a 6= 0 olması
durumunda ax = 1 denklemleri çözülebilir.
Postulat 1’den reel sayıların iyi bilinen aşağıdaki cebirsel kuralları elde edilebilir:
(−1)2 = 1,
(1.1)
0 · a = 0, −a = (−1) · a, −(−a) = a, a ∈ R,
(1.2)
−(a − b) = b − a, a, b ∈ R
(1.3)
a, b ∈ R ve ab = 0 ise a = 0 veya b = 0 sağlanır.
(1.4)
ve
Postulat 1 her ne kadar R üzerindeki tüm cebirsel kuralları belirlemede
yeterli olsa da reel sayılar sistemini tam olarak açıklamaz. Reel sayılar kümesi
üzerinde aynı zamanda bir sıralama bağıntısı vardır.
Postulat 2 [Sıralama Aksiyomları]. R × R üzerinde aşağıdaki özellikleri
sağlayan bir “<” bağıntısı vardır:
Trikotomi (Üç Hal) Özelliği. Her a, b ∈ R için aşağıdaki ifadelerin bir ve
yalnız bir tanesi doğrudur:
a < b, b < a veya a = b.
Transitiﬂik (Geçişme) Özelliği. Her a, b, c ∈ R için
a 0 ise ac < bc
ve
a a ile a < b kastedilmektedir. a ≤ b ve b ≥ a ile a < b veya a = b
anlatılmaktadır. a < b < c ile a < b ve b < c ifade edilmektedir. 2 < x < 1
şeklindeki bir eşitsizliğin hiç bir anlamı yoktur.
5
Yukarıda verildiği gibi iki tane Çarpma Özelliği vardır ve bu özellikleri kullanırken dikkatli olmak gerekir. Örneğin x < 1 olması x > 0 değil ise x2 < x
eşitsizliğinin gerçeklenmesini gerektirmez. Eğer x < 0 ise İkinci Çarpma Özelliği’ne göre x < 1 için x2 > x sağlanır.
a ≥ 0 özelliğini sağlayan bir a reel sayısı negatif olmayan, a > 0 ise pozitif
olarak adlandırılır.
Reel sayılar kümesi bazı özel alt kümeleri içerir. Bunlardan ilki 1 ile başlayan
ve 2 := 1 + 1, 3 := 2 + 1, · · · formunda elemanlarına ardışık olarak 1 eklemek
sureti ile elde edilen
N := {1, 2, · · · }
doğal (İngilizce karşılığı Natural) sayılar kümesidir. Ayrıca
Z := {· · · , −2, −1, 0, 1, 2, · · · }
şeklinde tanımlanan tamsayılar (Almanca karşılığı Zahl) kümesi,
nm
o
Q :=
: m, n ∈ Z, n 6= 0
n
olarak tanımlanan rasyonel (İngilizce karşılığı Quotients) sayılar kümesi ve
Qc = R\Q
irrasyonel (İngilizce karşılığı Irrationals) sayılar kümesi diğer önemli sayı kümeleridir. Rasyonel sayıların eşitliği aşağıdaki şekilde tanımlanır:
p
m
= ancak ve ancak mq = np.
n
q
Yukarıdaki sayı kümeleri arasında
N⊂Z⊂Q⊂R
şeklinde bir içerme bağıntısı vardır ve bu kümelerin her biri R reel sayılar
kümesinin bir özalt kümesidir. Örneğin her rasyonel sayı bir reel sayıdır. Gerçekten, rasyonel sayılar m/n := mn−1 şeklinde yazılabileceğinden ve Postulat
2’ye göre mn−1 bir√reel sayı olduğundan m/n rasyonel sayısı aynı zamanda bir
reel sayıdır. Fakat 2 reel sayısı rasyonel değildir.
N ve Z kümelerini tam olarak tanımlamadığımızdan bazı kabuller yapmamız
gerekmektedir:
Açıklama 1.2.1. N doğal sayılar ve Z tamsayılar kümelerinin aşağıdaki özellikleri gerçeklediği kabul edilsin:
i) Eğer n, m ∈ Z ise n + m, n − m ve nm sayıları da Z kümesine aittirler.
ii) Eğer n ∈ Z ise n ∈ N olması için gerek ve yeter şart n ≥ 1 eşitsizliğinin
sağlanmasıdır.
iii) 0 < n < 1 olacak şekilde bir n ∈ Z yoktur.
6
Bu özellikler kullanılarak Q rasyonel sayılar kümesinin Postulat 1’i sağladığı
gösterilebilir (bkz Alıştırma 1.2.10). Dikkat edilirse R’nin rasyonel sayılar kümesi hariç hiçbir özel alt kümesi Postulat 1’i gerçeklemez. N kümesi üç özellik
hariç diğer tüm özellikleri gerçekler: N kümesi 0 ∈
/ N olduğundan toplamanın
etkisiz elemanına sahip değildir, negatif eleman barındırmadığından toplamada
ters elemanları olamaz ve 1 dışında hiç bir elemanının çarpmada ters elemanı
yoktur. Z kümesi bir özellik hariç Postulat 1’in diğer tüm özellikleri gerçekler: 1
ve −1 hariç Z’nin sıfırdan farklı hiç bir elemanının çarpmada ters elemanı yoktur. Qc kümesi üç özellik hariç Postulat 1’in diğer özellikleri gerçekler: 0 ∈
/ R\Q
olduğundan toplamanın etkisiz elemanına sahip değildir, 1 ∈
/ R\Q olduğundan
çarpmanın etkisiz elemanı
yoktur. Ayrıca kapalılık√özelliğini√de her zaman sağ√
2
irrasyonel
olmakla birlikte 2 + (− 2) = 0 toplamı ve
lamaz.
Gerçekten,
√ √
2 · 2 = 2 çarpımı rasyoneldir.
Dikkat edilirse R’nin sözü edilen tüm alt kümeleri Postulat 2’yi gerçekler.
Buna göre Q Postulat 1 ve Postulat 2’yi sağlarken Kısım 1.3’de verilen Postulat 3’ü (Tamlık Aksiyomu) gerçeklemez. Benzer şekilde N, Z ve Qc kümelerinin
Postulat 1 ve Postulat 2’de verilen özelliklerden hangilerini sağladığı, hangilerini sağlamadığı okuyucu tarafından incelenmelidir. Verilen bu postulatlar
aslında R’yi karakterize ederler. R kümesi Postulat 1, Postulat 2 ve Postulat
3’ü gerçekleyen tek kümedir ve bu özelliğinden ötürü Tam Archimedean Sıralanmış Cisim olarak isimlendirilir.
Postulat 1 ve Postulat 2 kullanılarak reel sayıların sağladıkları tüm eşitlik ve
eşitsizlikler ispatlanabilir. Bu aşamada ispat kavramına kısaca değinelim. İspat
nedir? Her matematiksel sonuç (örnek, açıklama (remark), lemma ve teorem)
hipotez ve bir hüküm içerir. Bir ispatı yapmak için üç temel yöntem vardır:
matematiksel indüksiyon (tümevarım), doğrudan çıkarım (doğrudan ispat) ve
çelişki (olmayana ergi).
Matematiksel indüksiyon (veya tümevarım) verilen bir ifadenin tüm doğal
sayılar için doğru olduğunu ispatlamakta kullanılan oldukça pratik bir yöntemdir. Bu yönteme ifadenin önce 1 için (daha doğrusu, ifadenin doğruluğunun
başladığı doğal sayı için) doğru olduğu gösterilir. Daha sonra n doğal sayısı için
doğru olduğu farz edilir ve n + 1 doğal sayısı için doğru olduğu gösterilir. Bu da
herhangi bir doğal sayı için doğruysa sonraki için de doğru olacağını ispatladığından bütün doğal sayılar için geçerli bir ifade olduğu anlamına gelecektir. Bu
yöntem genelde sonsuz sayıda domino taşlarının dizilmesine benzetilir. n. taşın
devrilmesi bir sonraki yani n + 1. taşın da devrilmesi anlamına geleceğinden
taşların tamamı devrilecektir. Tabi ki yine n = 1 için doğruluğunu söylemek
gerekir. Bunun için de ilk taşı devirmemiz yeterli olacaktır.
Doğrudan çıkarım (veya doğrudan ispat) yönteminde hipotez doğru olarak
kabul edilir ve adım adım ilerleyerek istenen hükmün gerçeklendiği gösterilir.
Doğru olduğu gösterilmek istenen ifade, direk olarak, doğruluğu kanıtlanmış
başka ifadelerle veya aksiyomlarla türetilir.
Çelişki (veya olmayana ergi ) yönteminde hipotez doğru, doğruluğunu göstermeyi planlanan ifadenin yanlış olduğu kabul edilir ve adım adım işlem yapılarak bir çelişkiye ulaşılır. Çelişki, açık olarak yanlış olan ya da hipotez ile
çelişen bir ifadedir. Çelişkiye ulaşıldığı anda ispat tamamlanmış olur (bkz Te7
orem 1.2.9). Çünkü, başta yanlış olduğu kabul edilen ifadenin aslında doğru
olduğu ispatlanmış olur.
Peki verilen bir ifadenin yanlış olduğu nasıl “ispatlanır”? Bunun için ifadenin
hipotezini gerçekleyen fakat hüküm ile çelişen somut bir örnek vermek yeter.
Bu örneğe ters örnek adı verilir. Örneğin “x > 1 ise x2 − x − 2 6= 0 sağlanır.”
ifadesinin doğru olmadığını göstermek için 1’den büyük x = 2 sayısı seçilsin.
22 − 2 − 2 = 0 olduğundan verilen ifadenin yanlış olduğu gösterilmiş olur.
Aşağıda doğrudan çıkarım yöntemi kullanılarak bazı ispatlar yapılmaktadır.
sembolü ispatın ya da çözümün tamamlandığını ifade eder.
Örnek 1.2.2. a ∈ R olsun. Buna göre
a 6= 0 ise a2 > 0
(1.5)
olduğunu ve −1 < 0 < 1 eşitsizliğinin gerçeklendiğini ispatlayınız.
Kanıt. a 6= 0 olsun. Trikotomi özelliğine göre ya a < 0 ya da a > 0 sağlanır.
Durum 1. a > 0 olsun. Eşitsizliğin her iki tarafı Birinci Çarpma Özelliği kullanılarak a ile çarpılırsa a2 = a · a > 0 · a elde edilir. (1.2)’ye göre 0 · a = 0
olduğundan a2 > 0 sonucuna ulaşılır.
Durum 2. a < 0 olsun. Eşitsizliğin her iki tarafı İkinci Çarpma Özelliği kullanılırarak a ile çarpılırsa a2 = a · a > 0 · a elde edilir. (1.2)’ye göre 0 · a = 0
olduğundan a2 > 0 sonucuna ulaşılır.
Buna göre a 6= 0 ise a2 > 0 sağlanır. Diğer taraftan 1 6= 0 olduğundan 1 = 12 >
0’dır. Bu eşitsizliğin her iki tarafına −1 eklenirse 0 = 1 − 1 > 0 − 1 = −1 elde
edilir.
Örnek 1.2.3. a ∈ R olsun. Buna göre
0 < a < 1 ise 0 < a2 < a
ve
a > 1 ise a2 > a
(1.6)
olduğunu ispatlayınız.
Kanıt. 0 < a < 1 olsun. Eşitsizliğin her iki tarafı Birinci Çarpma Özelliği
kullanılırarak a ile çarpılırsa 0 = 0 · a < a2 < 1 · a = a yani 0 < a2 < a
elde edilir. Diğer taraftan a > 1 ise Örnek 1.2.2 ve Transitiﬂik Özelliği’ne göre
a > 0’dır. Dolayısıyla Birinci Çarpma Özelliği kullanılabilir. a > 1 ifadesinin
her iki tarafı a ile çarpılır ise a2 = a · a > 1 · a = a sonucuna ulaşılır.
Benzer şekilde (bkz Alıştırma 1.2.3) aşağıdaki ifadelerin doğruluğu gösterilebilir:
0 ≤ a 0.
b
değeri
>
(1.9)
a≥0
a<0
şeklide tanımlanan bir sayıdır.
Mutlak değere ilişkin bir özelliği ispatlamak istediğimizde genellikle parametrelerin pozitif, negatif veya sıfıra eşit olmasına bağlı olarak ispatı çeşitli alt
durumlara ayırıp bu alt durumlar üzerinde çalışırız. Aşağıda bu duruma ilişkin
bir örnek verilmektedir.
Açıklama 1.2.5. Mutlak değer çarpımsaldır. Yani her a, b ∈ R için |ab| = |a||b|
sağlanır.
Kanıt. Aşağıdaki dört durumu göz önüne alalım:
Durum 1. a = 0 veya b = 0 olsun. Bu durumda ab = 0’dır ve tanım gereği
|ab| = 0 = |a||b| sağlanır.
Durum 2. a > 0 ve b > 0 olsun. Birinci Çarpma Özelliği’ne göre ab > 0 · b = 0
sağlandığından mutlak değer tanımı gereği |ab| = ab = |a||b| elde edilir.
Durum 3. a > 0, b < 0 veya b > 0, a < 0 olsun. İspatı a > 0 ve b < 0 eşitsizliklerinin sağlandığı durumda yapmak yeter (çünkü simetriden ötürü a ile b’nin
yerlerini değiştirdiğimize b > 0 ve a < 0 kabulünü elde ederiz). İkinci Çarpma
Özelliği’ne göre ab < 0 olduğundan Tanım 1.2.4, asosyatiﬂik ve komütatiﬂik
özellikleri kullanılarak
|ab| = −(ab) = (−1)(ab) = a((−1)b) = a(−b) = |a||b|
sonucuna ulaşılır.
Durum 4. a < 0 ve b < 0 olsun. İkinci Çarpma Özelliği’ne göre ab > 0 olduğundan Tanım 1.2.4 kullanılarak
|ab| = ab = (−1)2 (ab) = (−a)(−b) = |a||b|
elde edilir.
Aşağıdaki teorem mutlak değer barındıran eşitsizlikleri çözmede oldukça sık
kullanılır.
Teorem 1.2.6 (Mutlak Değerin Temel Teoremi). a ∈ R ve M ≥ 0 olsun.
Buna göre |a| ≤ M olması için gerek ve yeter şart −M ≤ a ≤ M eşitsizliğinin
sağlanmasıdır.
9
Kanıt. (Gereklilik İspatı ⇒) a ∈ R ve |a| ≤ M olsun. Bu eşitsizliği −1 ile
çarparak −|a| ≥ −M elde edilir.
Durum 1. a ≥ 0 olsun. Bu durumda Tanım 1.2.4’e göre |a| = a sağlanır.
Dolayısıyla hipotez şartından
−M ≤ 0 ≤ |a| = a ≤ M
sonucu elde edilir.
Durum 2. a < 0 olsun. Bu durumda Tanım 1.2.4’e göre |a| = −a sağlanır.
Dolayısıyla hipotez şartından
−M ≤ −|a| = a < 0 ≤ M
ifadesine ulaşılır. Yani her iki durumda da −M ≤ a ≤ M eşitsizliği gerçeklenir.
(Yeterlilik İspatı ⇐) Tersine, −M ≤ a ≤ M eşitsizliği doğru olsun. Buna
göre a ≤ M ve −M ≤ a’dır. Dolayısıyla
a ≥ 0 olması durumunda |a| = a ≤ M
a < 0 olması durumunda |a| = −a ≤ M
elde edilir. Yani her iki durumda da |a| ≤ M sağlanır.
Not. Benzer şekilde |a| < M olması için gerek ve yeter şartın −M < a < M
eşitsizliğinin sağlanması olduğu gösterilebilir.
Aşağıdaki teorem mutlak değer kavramı için kullanışlı bir sonuçtur.
Teorem 1.2.7. Mutlak değer aşağıdaki üç özelliği gerçekler:
i) [Pozitiﬂik] Her a ∈ R için |a| ≥ 0’dır, öyleki |a| = 0 olması için gerek ve
yeter şart a = 0 eşitliğinin sağlanmasıdır.
ii) [Simetriklik] Her a, b ∈ R için |a − b| = |b − a| gerçeklenir.
iii) [Üçgen Eşitsizliği] Her a, b ∈ R için
|a + b| ≤ |a| + |b| ve ||a| − |b|| ≤ |a − b|
eşitsizlikleri geçerlidir.
Kanıt. i) Eğer a ≥ 0 ise |a| = a ≥ 0 sağlanır. Diğer taraftan a < 0 olması
durumunda Tanım 1.2.4 ve İkinci Çarpma Özelliği’ne göre |a| = −a = (−1)a >
0 elde edilir. Yani her a ∈ R için |a| ≥ 0 sonucuna ulaşılır.
Şimdi |a| = 0 olması için gerek ve yeter şartın a = 0 eşitliğinin sağlanması
olduğunu gösterelim. Öncelikle |a| = 0 olduğunu kabul edelim. Tanımından
10
ötürü a ≥ 0 için a = |a| = 0 ve a < 0 için a = −|a| = 0 gerçeklendiğinden
|a| = 0 olması a = 0 eşitliğini gerektirir. Tersine, a = 0 olsun. Mutlak değer
tanımına göre |0| = 0 sağlandığından |a| = 0 gerçeklenir.
ii) Açıklama 1.2.5 göz önüne alındığında
|a − b| = | − 1||a − b| = |b − a|
eşitliği elde edilir.
iii) İlk eşitsizliğin doğruluğunu ispatlamak için her x ∈ R reel sayısının |x| ≤
|x| eşitsizliğini sağladığı göz önüne alınsın. Buna göre Teorem 1.2.6 ifadesinden
−|a| ≤ a ≤ |a| ve −|b| ≤ b ≤ |b| elde edilir. Bu iki eşitsizliği taraf tarafa
topladığımızda
−(|a| + |b|) ≤ a + b ≤ |a| + |b|
sonucuna ulaşılır. Bu aşamada tekrar Teorem 1.2.6 kullanılır ise |a+b| ≤ |a|+|b|
eşitsizliği elde edilir.
İkinci eşitsizliği ispatlamak için (a − b) + b ifadesine ilk eşitsizlik uygulanır.
Buna göre
|a| − |b| = |a − b + b| − |b| ≤ |a − b| + |b| − |b| = |a − b|
elde edilir. Şimdi yukarıda a ile b’nin yerleri değiştirilir ve ii) sonucu kullanılır
ise
|b| − |a| = |b − a + a| − |a| ≤ |b − a| + |a| − |a| = |b − a| = |a − b|,
ve bu ifadeyi −1 ile çarparak
|a| − |b| ≥ −|a − b|
sonucu bulunur. Dolayısıyla
−|a − b| ≤ |a| − |b| ≤ |a − b|
eşitsizliği doğru olduğundan Teorem 1.2.6’ya göre ||a| − |b|| ≤ |a − b| ifadesine
ulaşılır.
Yukarıdaki son eşitsizlik ispatlanırken aynı zamanda her a, b ∈ R için |a| −
|b| ≤ |a − b| olduğu sonucu da elde edildi ki bu ifade sıkça kullanılacaktır.
Uyarı. Burada dikkat edilmesi gereken bir husus Toplama Özelliği ve mutlak
değerin beraber kullanılıp b < c ise |a + b| < |a + c| şeklinde bir eşitsizliğin her
zaman geçerli olduğunun düşünülmemesidir. Bu eşitsizlik sadece a + b ve a + c
ifadelerinin her ikisi de negatif değil ise doğrudur. Örneğin a = 1, b = −5 ve
c = −1 ise b < c sağlanır fakat |a + b| = |1 + (−5)| = 4 > 0 = |1 + (−1)| =
|a + c|’dır.
11
Örnek 1.2.8. Eğer −2 < x < 1 ise |x2 − x| < 6 olduğunu gösteriniz.
Kanıt. Hipoteze göre −2 < x < 1 olduğundan −2 < x < 1 < 2 yani −2 < x <
2 dolayısıyla |x| < 2 sağlanır. Dolayısıyla üçgen eşitsizliği ve Açıklama 1.2.5
kullanıldığında
|x2 − x| ≤ |x2 | + |x| = |x|2 + |x| < 22 + 2 = 6
elde edilir.
Şimdi Trikotami Özelliği’ne karşılık gelen ve çokça kullanacağımız aşağıdaki
sonucu verelim:
Teorem 1.2.9. x, y, a ∈ R olsun.
i) Her ε > 0 sayısı için x < y + ε olması için gerek ve yeter şart x ≤ y
eşitsizliğinin gerçeklenmesidir.
ii) Her ε > 0 sayısı için x > y − ε olması için gerek ve yeter şart x ≥ y
eşitsizliğinin gerçeklenmesidir.
iii) Her ε > 0 sayısı için |a| < ε olması için gerek ve yeter şart a = 0
eşitliğinin gerçeklenmesidir.
Kanıt. i) Gereklilik kısmının ispatını çelişki yöntemi ile elde edeceğiz. Buna
göre, her ε > 0 sayısı için x < y + ε sağlansın fakat buna karşılık x > y olsun.
x > y olduğundan x − y farkı pozitiftir. ε0 = x − y > 0 denirse y + ε0 = x
olarak ifade edilebilir. Dolayısıyla, Trikotami Özelliği’ne göre y+ε0 değeri x’den
büyük olamaz. Bu ise ε = ε0 için teorem hipotezi ile çelişir. Bu çelişkiye neden
x > y olarak alınmasıdır. Yani, x ≤ y eşitsizliği geçerlidir.
Tersine, ε > 0 sayısı verilsin ve x ≤ y sağlansın. Buna göre ya x = y ya
da x < y’dir. Eğer x < y ise Toplama ve Transitiﬂik Özellikleri’nden x + 0 <
y + 0 < y + ε yazılabilir. Eğer x = y ise Toplama Özelliği’ne göre x < y + ε
sağlanır. Bu durumda her ε > 0 sayısı için x < y + ε eşitsizliği her iki durumda
da gerçeklenir.
ii) Her ε > 0 sayısı için x > y − ε olsun. İkinci Çarpma Özelliği’ne göre bu
ifade −x < −y + ε eşitsizliğine denktir. Dolayısıyla i) şıkkına göre −x ≤ −y
olduğu sonucu elde edilir. Bu ise İkinci Çarpma Özelliği göz önüne alındığında
x ≥ y eşitsizliğinin doğruluğunu gösterir.
iii) Her ε > 0 sayısı için |a| < ε = 0 + ε olsun. i) neticesine göre bu ifade
|a| ≤ 0 olmasına denktir. Diğer taraftan her zaman |a| ≥ 0 sağlandığından
Trikotami kuralı gereğince |a| = 0’dır. Bu ise Teorem 1.2.7’nin i) şıkkına göre
a = 0 olduğu anlamına gelir.
12
a ve b iki reel sayı olsun. Bu durumda
[a, b] := {x ∈ R : a ≤ x ≤ b}, [a, ∞) := {x ∈ R : a ≤ x},
(−∞, b] := {x ∈ R : x ≤ b} veya (−∞, ∞) := R
formundaki bir kümeye kapalı aralık,
(a, b) := {x ∈ R : a < x < b}, (a, ∞) := {x ∈ R : a < x},
(−∞, b) := {x ∈ R : x < b} veya (−∞, ∞) := R
formundaki bir kümeye ise açık aralık adı verilir.
Aralık ile ya bir kapalı aralık ya bir açık aralık ya da
[a, b) := {x ∈ R : a ≤ x < b} veya (a, b] := {x ∈ R : a < x ≤ b}
formundaki bir küme kastedilmektedir.
a < b olması durumunda [a, b], [a, b), (a, b] ve (a, b) aralıkları reel sayı doğrusu üzerinde bir doğru parçasına tekabül eder, eğer b < a ise bu “aralıkların”
hepsi boş kümedir.
−∞ < a ≤ b < ∞ olmak üzere bir I aralığının sınırlı olarak adlandırılması
için gerek ve yeter şart [a, b], (a, b), [a, b) veya (a, b] formlarından birine sahip
olmasıdır. Bu durumda a ve b sayılarına I aralığının uç noktalar ı denir. Sınırlı
olmayan diğer tüm aralıklar sınırsız olarak isimlendirilir.
a, b uç noktaları a = b eşitliğini sağlayan bir aralığa dejenere, a < b eşitsizliğini sağlayan bir aralığa ise dejenere olmayan aralık adı verilir. Tanıma göre
bir dejenere açık aralık boş kümedir ve dejenere kapalı aralık ise bir noktadan
ibarettir.
Mutlak değer uzunluk kavramı ile yakından ilişkilidir. a ve b uç noktalarına
sahip bir kapalı aralığın uzunluğu |I| := |b − a| olarak, a, b ∈ R gibi herhangi
iki sayının arasındaki uzaklık ise |a − b| şeklinde tanımlanır.
Aralıklar kullanılarak eşitsizlikler ifade edilebilir. Örneğin, Teorem 1.2.6
istenirse |a| ≤ M olması için gerek ve yeter şart a’nın [−M, M ] kapalı aralığında
yer almasıdır, benzer şekilde Teorem 1.2.9’da iii) ifadesi a sayısının ε > 0 olmak
üzere (−ε, ε) açık aralığında yer alması için gerek ve yeter şart a = 0 eşitliğinin
gerçeklenmesidir şeklinde yazılabilir.
Alıştırmalar
1.2.1. a, b, c, d ∈ R olmak üzere aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise
birer ters örnek veriniz.
a)
b)
c)
d)
a bd’dir.
a ≤ b ve c > 1 ise |a + c| ≤ |b + c|’dir.
a ≤ b ve b ≤ a + c ise |a − b| ≤ c’dir.
Her ε > 0 için a < b − ε ise a < 0’dır.
Çözüm.
13
a)
b)
c)
d)
Yanlış. a = 2/3, b = 1, c = −2 ve d = −1 alınır ise istenilen gösterilmiş olur.
Yanlış. a = −4, b = −1 ve c = 2 alınır ise istenilen gösterilmiş olur.
Doğru. a ≤ b ve b ≤ a + c olduğundan |a − b| = b − a ≤ a + c − a = c sağlanır.
Eğer b ≤ 0 ise a 0 ise ε = b için
a < b − ε = 0 elde edilir.
1.2.2. a, b, c ∈ R ve a ≤ b olsun.
a) a + c ≤ b + c olduğunu ispatlayınız.
b) c ≥ 0 ise a · c ≤ b · c eşitsizliğinin geçerliliğini gösteriniz.
Çözüm.
a) a < b ise Toplama Özelliği’ne göre a+c < b+c sağlanır. a = b olması durumunda
+ bir fonksiyon olduğundan a + c = b + c gerçeklenir. Buna göre her a ≤ b için
a + c ≤ b + c eşitsizliği doğrudur.
b) c = 0 ise ac = 0 = bc ifadesi sağlanacağından c > 0 olduğunu kabul edebiliriz.
Eğer a < b ise Çarpma Özelliği’ne göre ac < bc gerçeklenir. a = b olması
durumunda · bir fonksiyon olduğundan ac = bc sağlanır. Buna göre her a ≤ b
ve c ≥ 0 için ac ≤ bc eşitsizliği doğrudur.
1.2.3. (1.7), (1.8) ve (1.9) ifadelerini ispatlayınız. Ayrıca a ≥ 0 veya a > 0 koşullarının
kaldırılması durumunda bu ifadelerin gerçeklenemediğini gösteriniz.
Çözüm.
a) 0 ≤ a < b ve 0 ≤ c < d ise ac < bd sağlanır. Gerçekten, ilk eşitsizliği c ve
ikinci eşitsizliği b ile çarparsak 0 ≤ ac < bc ve 0 ≤ bc < bd elde edilir. Bu ise
Transitiﬂik Özelliği’ne göre ac < bd olduğu √
anlamına gelir.
√
b) 0 ≤ a < b ise 0 ≤ a2 < b2 ve 0 ≤ a < b sağlanır. Gerçekten, 0 ≤ a < b
olduğundan (1.7)’ye göre 0 ≤ a2 < ab ve 0 √
≤ ab < b2 yani √
0 ≤ a2 1/b > 0 sağlanır. Gerçekten, eğer 1/a ≤ 1/b olsaydı
Çarpma Özelliği’ne göre b = ab(1/a) ≤ ab(1/b) = a çelişkisi elde edilirdir.
Diğer taraftan 1/b ≤ 0 olsaydı b = b2 (1/b) ≤ 0 çelişkisine ulaşılırdı.
d) a < 0 için verilen ifadelerinin doğru olması gerekmediğini göstermek için a =
−2, b = −1, c = 2 ve d = 5 alalım. Bu durumda a < b ve c < d iken ac = −4
olup bd = −5 değerinden küçük değildir. Ayrıca a2 = 4 sayısı da b2 = 1’den
küçük değildir. Diğer taraftan 1/a = −1/2 değeri de 1/b = −1 sayısından küçük
kalmaz.
1.2.4. Bir a ∈ R sayısının pozitif kısmı
a+ :=
|a| + a
,
2
a− :=
|a| − a
,
2
negatif kısmı ise
olarak tanımlanır.
a) a = a+ − a− ve |a| = a+ + a− olduğunu gösteriniz.
14
b) Aşağıdaki ifadelerin doğruluğunu gösteriniz:


a a ≥ 0
0
a+ =
ve a− =
0 a ≤ 0
−a
a≥0
a ≤ 0.
Çözüm.
a) Verilen tanımlara göre
a+ − a− =
ve
a+ + a− =
|a| + a
|a| − a
|a| + a − |a| + a
2a
−
=
=
= a,
2
2
2
2
|a| − a
|a| + a + |a| − a
2|a|
|a| + a
+
=
=
= |a|
2
2
2
2
sağlanır.
b) Mutlak değer tanımına göre a ≥ 0 ise a+ = (a + a)/2 = a ve a < 0 ise
a+ = (−a + a)/2 = 0 olur. Benzer şekilde a ≥ 0 ise a− = (a − a)/2 = 0 ve
a < 0 ise a− = (−a − a)/2 = −a gerçeklenir.
1.2.5. Aşağıdaki eşitsizlikleri sağlayan x ∈ R sayılarını tespit ediniz.
a) |2x + 1| < 7
b) |2 − x| < 2
c) |x3 − 3x + 1| < x3
x
<1
d) x−1
2
e) 4xx2 −1 < 14
Çözüm.
a) |2x + 1| < 7 ancak ve yalnız −7 < 2x + 1 < 7 ancak ve yalnız −8 < 2x < 6
ancak ve yalnız −4 < x < 3.
b) |2 − x| < 2 ancak ve yalnız −2 < 2 − x < 2 ancak ve yalnız −4 < −x < 0 ancak
ve yalnız 0 < x < 4.
c) |x3 − 3x + 1| < x3 ancak ve yalnız −x3 < x3 − 3x + 1 < x3 ancak ve yalnız
−3x + 1 < 0 yani 3x − 1 > 0 ve 2x3 − 3x + 1 > 0. 3x − 1 > 0 eşitsizliği x > 1/3
2
olmasına denktir. Diğer taraftan 2x3 − 3x
√ + 1 = (x − 1)(2x 3+ 2x − 1) = 0
ifadesini sağlayan√değerler x = 1, (−1 √
± 3)/2 olduğundan 2x − 3x + 1 > 0
(−1 + 3)/2 ya da x > 1 eşitsizliğine karşılık
eşitsizliği (−1 − 3)/2 < x < √
gelir. Dolayısıyla çözüm (1/3, ( 3 − 1)/2) ∪ (1, ∞) olarak bulunur.
d) Verilen ifadenin her iki yanını x − 1’in pozitif veya negatif olduğunu göz önüne
almadan x − 1 ile çarpamayız.
Durum 1. x − 1 > 0 olsun. Bu durumda x < x − 1 yani 0 < −1 olacağından
eşitsizliği sağlayan x değerlerinin kümesi boştur.
Durum 2. x−1 < 0 olsun. Bu durumda İkinci Çarpma Özelliği’ne göre x > x−1
yani 0 > −1 olması her x reel sayısı için doğru olduğundan çözüm aralığı
(−∞, 1)’dir.
e) Durum 1. 4x2 − 1 > 0 olsun. Çapraz çarpma yaparak 4x2 < 4x2 − 1 yani boş
küme elde edilir.
Durum 1. 4x2 − 1 < 0 olsun. Bu durumda İkinci Çarpma Özelliği’ne göre
4x2 > 4x2 − 1 yani 0 > −1 olması her x reel sayısı için doğru olduğundan
çözüm aralığı (−1/2, 1/2)’dir.
15
1.2.6. a, b ∈ R olsun.
a)
b)
c)
d)
√
a > 2 ve b = 1 + a −
√1 ise 2 < b < a olduğunu ispatlayınız.
2 < a < 3 ve b = 2 + √a − 2 ise 0 < a 2 olsun. Bu durumda a−1 > 1 yani 1 < a − 1 < a−1 sağlanır. Dolayısıyla
√
2 < b = 1 + a − 1 < 1 + (a − 1) gerçeklenir.
√
b) 2 < a < 3 olsun. Bu durumda 0 < a − 2 < 1 yani 0 < a − 2 < a − 2 < 1
√
sağlanır. Dolayısıyla 0 < a < 2 + a − 2 = b gerçeklenir.
c) 0 < a < 1 olsun. Bu durumda 0 > −a > −1 yani 0 < 1 − a < 1 sağlanır.
√
√
√
1 − a reel olduğundan 1−a < 1 − a doğrudur. Dolayısıyla b = 1− 1 − a <
1 − (1 − a) = a gerçeklenir.
√
d) 3 < a < 5 olsun. Bu durumda 1 < a − 2 < 3 yani 1 < a − 2 < a − 2 sağlanır.
√
Dolayısıyla 3 < 2 + a − 2 = b < a gerçeklenir.
1.2.7. a, b ∈ R sayılarının aritmetik ortalaması
√ A(a, b) = (a + b)/2 ve a, b ∈ [0, ∞)
sayılarının geometrik ortalaması ise G(a, b) = ab olarak tanımlanır. Eğer 0 ≤ a ≤ b
ise a ≤ G(a, b) ≤ A(a, b) ≤ b olduğunu ispatlayınız. Ayrıca G(a, b) = A(a, b) eşitliğinin sağlanması için gerek ve yeter şartın a = b ifadesinin gerçeklenmesi olduğunu
gösteriniz.
√
√
√
Çözüm.
Her a, b ∈ [0, ∞) için a + b − 2 ab = ( a − b)2 ≥ 0 sağlanır. Buna göre
√
2 ab ≤ a + b ve dolayısyla G(a, b) ≤ A(a, b) gerçeklenir. Diğer
√ 0≤a≤b
√ taraftan
olduğundan A(a, b) = (a + b)/2 ≤ 2b/2 = b ve G(a,√b) = ab ≥ a2 = a elde
edilir. Son
b) ancak
√ olarak, A(a, b) = G(a,
√ ve yalnız 2 ab = a + b ancak ve yalnız
√
√
( a − b)2 = 0 ancak ve yalnız a = b ancak ve yanlız a = b ifadesine ulaşılır.
1.2.8. x ∈ R olsun.
a)
b)
c)
d)
|x| ≤ 2 ise |x2 − 4| ≤ 4|x − 2| olduğunu ispatlayınız.
|x| ≤ 1 ise |x2 + 2x − 3| ≤ 4|x − 1| olduğunu ispatlayınız.
−3 ≤ x ≤ 2 ise |x2 + x − 6| ≤ 6|x − 2| olduğunu ispatlayınız.
−1 < x < 0 ise |x3 − 2x + 1| < 1.26|x − 1| olduğunu ispatlayınız.
Çözüm.
a) |x| ≤ 2 ve |x + 2| ≤ |x| + 2 olduğundan |x2 − 4| = |x + 2||x − 2| ≤ 4|x − 2| elde
edilir.
b) |x| ≤ 1 ve |x + 3| ≤ |x| + 3 olduğundan |x2 + 2x − 3| = |x + 3||x − 1| ≤ 4|x − 1|
elde edilir.
c) −3 ≤ x ≤ 2 ve |x−2| ≤ |x|+2 olduğundan |x2 +x−6| = |x+3||x−2| ≤ 6|x−2|
elde edilir.
d) −1 < x < 0 ve x2 + x − 1 fadesi (−1, 0) aralığında minimum değerini −1.25
noktasında aldığından |x3 − 2x + 1| = |x2 + x − 1||x − 1| < 5|x − 1|/4 elde edilir.
1.2.9. Aşağıdaki eşitsizlikleri gerçekleyen tüm n ∈ N değerlerini tespit ediniz.
a)
b)
c)
1−n
< 0.01
1−n2
n2 +2n+3
2n3 +5n2 +8n+3
n−1
<
n3 −n2 +n−1
< 0.025
0.002
16
Çözüm.
a) (1 − n)/(1 − n2 ) = 1/(1 + n) olduğundan 1/(n + 1) < 0.01 = 1/100 elde edilir.
Her n ∈ N için 1 + n > 0 olduğundan n + 1 > 100 yani n > 99 sonucuna ulaşılır.
b) Sadeleştirme yapıldığında verilen ifadenin 1/(2n + 1) < 1/40 yani 2n + 1 > 40
eşitsizliğine denk olduğu elde edilir. Buna göre n > 39/2 dolayısıyla n ≥ 20
eşitsizliğine ulaşılır.
√
c) Verilen eşitsizlik n2 + 1 > 500 olmasına denktir. Buna göre n > 499 ≈ 22.33
yani n > 23 eşitsizliği elde edilir.
1.2.10.
a) m/n rasyonel sayısını m · n−1 ∈ R şeklinde yorumlayıp m, n, p, q, ℓ ∈ Z
ve n, q, ℓ 6= 0 olmak üzere Postulat 1’i kullanarak aşağıdaki ifadelerin doğruluğunu gösteriniz:
p
mq + np
m
+ =
,
n
q
nq
m p
mp
· =
,
n q
nq
−
ℓ −1
m
−m
n
=
ve
= .
n
n
n
ℓ
b) Açıklama 1.2.1’i kullanarak Postulat 1’de R yerine Q olması durumunda Postulat 1’in gerçeklendiğini gösteriniz.
c) Bir rasyonel sayının irrasyonel bir sayı ile toplamının her zaman irrasyonel
olduğunu ispatlayınız. Rasyonel bir sayı ile irrasyonel bir sayının çarpım sonucu
hakkında yorum yapınız.
d) n, q > 0 olmak üzere m/n, p/q ∈ R sayıları göz önüne alınsın. Aşağıdaki ifadenin
doğruluğunu kanıtlayınız:
p
m
< eşitsizliği için gerek ve yeter şart mq < np olmasıdır.
n
q
(Bu sonuç rasyonel sayılara kısıtlanarak Q üzerinde “<” tanımı elde edilir.)
1.2.11. Her a, b, c, d ∈ R için
(ab + cd)2 ≤ (a2 + c2 )(b2 + d2 )
eşitsizliğinin gerçeklendiğini gösteriniz.
1.2.12.
a) R+ ile pozitif reel sayılar kümesi gösterilsin. Buna göre R+ ’nin aşağıdaki iki özelliği gerçeklediğini gösteriniz:
i) Her a ∈ R için aşağıdakilerin bir ve sadece bir tanesi doğrudur:
x ∈ R+ ,
−x ∈ R+ veya x = 0.
ii) x, y ∈ R+ olmak üzere x + y ve x · y sayıları da R+ kümesine aittir.
b) R kümesi i) ve ii) ile verilen özellikleri gerçekleyen bir R+ alt kümesini kapsasın
(bu küme pozitif reel sayılar kümesinin kendisi olmak zorunda değildir). x ≺ y
ile y − x ∈ R+ tanımlansın. Buna göre Postulat 2’de < yerine ≺ yazılması
durumunda Postulat 2’nin gerçeklendiğini gösteriniz.
17
1.3
Tamlık Aksiyomu
Bu bölümde R reel sayılara ilişkin üç postulatın sonuncusu üzerinde durulacaktır. İlk iki postulatın her ikisini de gerçekleyen R ve Q kümeleri arasında bir
ayırım özelliği görecek üçüncü postulatı formülüze etmek için aşağıdaki konsept
kullanılır.
Tanım 1.3.1. E reel sayıların boştan farklı bir alt kümesi olsun. Buna göre
i) E kümesinin üstten sınırlı olarak adlandırılması için gerek ve yeter şart
her a ∈ E için a ≤ M olacak şekilde bir M ∈ R sayısının var olmasıdır.
Bu durumda M sayısına E kümesinin bir üst sınırı denir.
ii) Bir s sayısının E kümesinin supremumu olarak adlandırılması için gerek
ve yeter şart s’in E kümesinin bir üst sınırı olması ve E’nin tüm M üst
sınırları için s ≤ M eşitsizliğinin gerçeklenmesidir. Bu durumda E kümesi
sonlu bir s supremumuna sahiptir denir ve s = sup E yazılır.
Tanım 1.3.1 ii)’ye göre bir E kümesinin supremumu (eğer varsa) E’nin
üst sınırlarının en küçüğüdür. Yine tanıma göre herhangi bir E ⊂ R kümesi
verildiğinde s = sup E olduğunu ispatlamak için hem s’in bir üst sınır olduğunu
hem de üst sınırların en küçüğü olduğunu göstermek gerekir.
Örnek 1.3.2. E = [0, 1] olsun. Buna göre sup E = 1’dir.
Kanıt. Aralığın tanımından 1 sayısının E kümesinin bir üst sınırı olduğu görülür. Zira her x ∈ [0, 1] için x ≤ 1 gerçeklenir. Diğer taraftan M sayısı E
kümesinin bir üst sınırı olsun. Buna göre her x ∈ E için M ≥ x eşitsizliği sağlanır. 1 ∈ E olduğundan aynı zamanda M ≥ 1 eşitsizliği doğrudur. Buradan
E’nin en küçük üst sınırının 1 olduğu sonucuna ulaşılır.
Aşağıdaki iki açıklama verilen bir kümenin kaç tane üst sınırı ve supremumu
olabilir sorusuna cevap mahiyetindedir.
Açıklama 1.3.3. Bir kümenin bir üst sınırı varsa sonsuz sayıda üst sınırı
vardır.
Kanıt. Eğer M0 sayısı E kümesinin bir üst sınırı ise M > M0 eşitsizliğini
gerçekleyen tüm M sayıları da E kümesinin üst sınırı olurlar. Bir sayıdan büyük
sonsuz tane reel sayı olduğundan E kümesinin sonsuz sayıda üst sınıra sahip
olduğu sonucu elde edilir.
Açıklama 1.3.4. Eğer bir kümenin supremumu varsa tek türlü belirlidir.
18
Kanıt. E kümesinin s1 ve s2 gibi iki supremumu olsun. Supremum tanımına
göre hem s1 hem de s2 sayıları E kümesinin birer üst sınırıdır. Ayrıca Tanım
1.3.1 ii)’ye göre s1 ≤ s2 ve s2 ≤ s1 sağlanır. Dolayısıyla, Trikotami Özelliği
gereği s1 = s2 olmalıdır.
Not. Yukarıdaki ispat genel bir prensibi göstermektedir. a = b olduğu kanıtlanmak istenildiğinde ayrı ayrı a ≤ b ve b ≤ a olduğunu ispatlamak genellikle
daha kolaydır.
Teorem 1.3.5 (Supremum için Yaklaşım Özelliği). E kümesinin sonlu bir
supremumu var olsun. Buna göre ε > 0 herhangi bir pozitif sayı olmak üzere
sup E − ε < a ≤ sup E
eşitsizliğini gerçekleyen bir a ∈ E noktası vardır.
Kanıt. Farz edelim ki teorem yanlış olsun. Buna göre öyle bir ε0 > 0 sayısı
vardır ki E kümesinin hiç bir elemanı s0 := sup E − ε0 ile sup E arasında yer
almaz. sup E sayısı E kümesinin bir üst sınırı olduğundan her a ∈ E için a ≤ s0
sağlanır. Buna göre s0 sayısı E kümesinin bir üst sınırı olur. Dolayısıyla, Tanım
1.3.1 ii)’den sup E ≤ s0 = sup E−ε0 eşitsizliği gerçeklenir. Bu eşitsizliğin her iki
tarafına ε0 − sup E eklenir ise ε0 ≤ 0 elde edilir ki bu durum bir çelişkidir.
Yaklaşım Özelliği kullanılarak tamsayıların herhangi bir alt kümesinin supremumunun yine bir tamsayı olduğu gösterilebilir.
Teorem 1.3.6. Eğer E ⊂ Z kümesinin bir supremumu varsa sup E ∈ E’dir.
Özel olarak, sadece tamsayıları içeren bir kümenin supremumu varsa yine bir
tamsayıdır.
Kanıt. s := sup E olsun. Yaklaşım Özelliği kullanılarak s − 1 < x0 ≤ s eşitsizliğini sağlayan bir x0 ∈ E tamsayısı seçilsin. Eğer s = x0 ise s ∈ E olacağından
istenen sağlanır. Yani sup E bir tamsayıdır. Diğer durumda s − 1 < x0 < s
olur ve yine Yaklaşım Özelliği kullanılarak x0 < x1 < s eşitsizliğini sağlayan
bir x1 ∈ E seçilebilir. x0 < x1 < s eşitsizliğinin her üç tarafından x0 çıkartılır
ise 0 < x1 − x0 < s − x0 elde edilir. Diğer taraftan s − 1 < x0 olduğundan
−x0 < 1 − s yazılabilir. Buna göre 0 < x1 − x0 < s + (1 − s) = 1 sonucuna
ulaşılır. Dolayısıyla x1 −x0 ∈ Z∩(0, 1) neticesi elde edilir ki bu durum Açıklama
1.2.1 iii) ile çelişir. Şu halde s ∈ E olmak zorundadır.
R ile ilgili yapılacak son varsayım supremumun varlığı ile ilgilidir:
19
Postulat 3 [Tamlık Aksiyomu]. E reel sayıların boştan farklı ve üsten sınırlı
bir alt kümesi ise E’nin sonlu bir supremumu vardır.
Tamlık Aksiyomu sıklıkla kullanılan bir olgudur. Bu aksiyomun ilk iki uygulaması tamsayıların ve reel sayılar içerisinde rasyonel sayıların dağılımlarını
ortaya koyar.
Teorem 1.3.7 (Archimedean Özelliği). a > 0 olmak üzere her a ve b reel sayısı
için b < na eşitsizliğini sağlayacak şekilde bir n ∈ N tamsayısı vardır.
Strateji: İspatın arkasında yatan mantık gayet basittir. Tamlık Aksiyomu ve
Teorem 1.3.6’ya göre tamsayıların boştan farklı üstten sınırlı her alt kümesi
bir “en büyük” tamsayıya sahiptir. Eğer k0 a ≤ b koşulunu sağlayan en büyük
tamsayı k0 ise n = k0 + 1 için, ki bu durumda n sayısı k0 ’dan büyüktür, na > b
eşitsizliği gerçeklenir. Bu aşamada iki olgunun üzerinde durulması gerekir: (1)
E := {k ∈ N : ka ≤ b} kümesi üstten sınırlı mıdır? (2) E kümesi boştan farklı
mıdır? İkinci sorunun cevabı b < a olup olmamasına bağlıdır. Şimdi detayları
verebiliriz.
Kanıt. Eğer b < a ise n = 1 için istenen sağlanır. a ≤ b olsun ve E = {k ∈ N :
ka ≤ b} kümesi göz önüne alınsın. E kümesi en azından 1 doğal sayısını içerdiğinden boştan farklıdır. ka ≤ b ifadesini sağlayan k ∈ E için, a > 0 olduğundan
Birinci Çarpma Özelliği’ne göre k ≤ b/a yazılabilir. Bu ise E kümesi b/a ile üsten sınırlıdır demektir. Dolayısıyla Tamlık Aksiyomu ve Teorem 1.3.6’ya göre,
E kümesi sonlu bir s supremumuna sahiptir öyle ki bu s sayısı aynı zamanda
E kümesinin elemanıdır. Yani s ∈ N gerçeklenir.
n = s+1 olsun. Buna göre n ∈ N’dir ve s’den büyük olduğundan E kümesine
ait olamaz. Şu halde na > b sağlanır.
Örnek 1.3.2 ve Teorem 1.3.6 göz önüne alındığında E’nin supremumunun
yine E kümesinin elemanı olduğu gözlenmektedir. Fakat durum her zaman
böyle olmayabilir.
n
o
n
o
Örnek 1.3.8. A = 1, 21 , 81 , · · · ve B = 21 , 32 , 43 , · · · kümeleri göz önüne
alınsın. sup A = sup B = 1 olduğunu kanıtlayınız.
Kanıt. 1 sayısının her iki kümenin de bir üst sınırı olduğu açıktır. Bu durumda
gösterilmesi gereken her iki küme için de 1’in en küçük üst sınır olduğudur. A
kümesi göz önüne alınsın. 1 ∈ A olduğundan A’nın herhangi bir M üst sınırı
için M ≥ 1 gerçeklenir. Dolayısyla sup A = 1 olduğu sonucu elde edilir. Diğer
taraftan, M sayısı B kümesinin bir üst sınırı olsun, öyleki M < 1 eşitsizliğini
sağlasın. Buna göre 1 − M > 0 olduğundan 1/(1 − M ) ∈ R gerçeklenir.
1
1 − M pozitif olduğundan ab = 1−M
olarak alındığında Archimedean Özelliği’ne göre n > 1/(1 − M ) eşitsizliğini sağlayan bir n ∈ N sayısı vardır. Buna
20
1
göre n > 1−M
olduğundan n(1 − M ) > 1 yani 1 − M > n1 yazılabilir. Bu ise
−M > n1 − 1 ya da M < 1 − n1 demektir. Şimdi x0 := 1 − 1/n diyelim. B
kümesinin elemanları
n1 2 3
o n
o
1
1
1
B=
, , ,··· = 1 − ,1 − ,1 − ,···
2 3 4
2
3
4
yani her n = 2, 3, · · · için 1− n1 formunda olduğundan x0 ∈ B’dir. Fakat M < x0
olması M sayısının B kümesinin bir üst sınırı olması ile çelişir. Şu halde M < 1
olamaz. Yani sup B = 1’dir.
Teorem 1.3.9 (Rasyonel Sayıların Yoğunluğu). a < b koşulunu sağlayan a ve
b reel sayıları verilsin. Buna göre a < q 0 ve E := {k ∈ N :
k/n ≤ a} kümesinin k0 gibi bir supremumu olduğunu farz edelim. Buna göre
m := k0 + 1 sayısı E’nin supremumundan büyük olmakla birlikte E kümesine
ait değildir. Dolayısıyla m/n > a eşitsizliği gerçeklenir. Peki aradığımız kesir
bu mudur? Ayrıca m/n < b eşitsizliği sağlanır mı? Cevap eğer n sayısı yeterince
büyük değil ise istenenin sağlanmadığı yönündedir. Bunu görmek için somut bir
örnek verelim: a = 2/3 ve b = 1 olsun. Eğer n = 1 ise E kümesi k1 ≤ 23 özelliğini
sağlayan k ∈ N sayılarını içereceğinden E boş kümedir ve supremumu yoktur.
n = 2 olması durumunda E kümesi k2 ≤ 32 yani k ≤ 43 özelliğini sağlayan
k ∈ N sayılarını içereceğinden E kümesinin supremumu k0 = 1’e eşittir. Benzer
şekilde n = 3 olması durumunda E kümesi k3 ≤ 32 yani k ≤ 2 özelliğini sağlayan
k ∈ N sayılarını içereceğinden E kümesinin supremumu k0 = 2’ye eşittir. Her
iki durumda da (k0 + 1)/n = 1’dir ki bu değer istenenden büyüktür. Fakat
n = 4 olması durumunda E kümesi k4 ≤ 32 yani k ≤ 83 özelliğini sağlayan
k ∈ N sayılarını içereceğinden E kümesinin supremumu k0 = 2’ye eşittir ve
(k0 + 1)/4 = 3/4 elde edilir ki bu değer istenildiği üzere b = 1’den küçüktür.
Her a < b için yeterince büyük bir n sayısının, k0 yukarıda anlatıldığı gibi
seçilmek üzere, (k0 +1)/n < b eşitsizliğini sağlayacak şekilde var olduğunu nasıl
ispatlamalıyız? Sorunun cevabı k0 ’ın k0 /n ≤ a eşitsizliğini sağlayacak şekilde
seçilmesi olgusuna dayanır. En kötü durumda a = k0 /n olsun. Bu durumda
b > (k0 + 1)/n eşitsizliği
b>
k0
1
1
k0 + 1
=
+ =a+
n
n
n
n
yani b − a > 1/n olduğu anlamına gelirdi ki Archimedean Özelliğine göre bu
şekilde bir n her zaman seçilebilir.
Peki sup E’nin var olduğu varsayımı için ne söylenebilir? Bu durum E’nin
boştan farklı ve üstten sınırlı olmasını gerektirir. Eğer n sabitlenir ise bu durumda E kümesi na ile üstten sınırlı olur. Fakat E kümesinin boştan farklı
olmasının tek yolu 1 ∈ E yani 1/n ≤ a olması ile mümkündür. Bu durum n
21
üzerinde ikinci bir kısıtlama yapılmasını gerektirir. Bu noktadan sonra ispatımıza geçebiliriz.
Kanıt. a > 0 olsun. Dolayısıyla b − a > 0’dır ve Archimedean Özelliği’ne göre
n > max
1 o
a b−a
n1
,
eşitsizliğini sağlayan bir n ∈ N sayısı, 1/n < a ve n1/n < bo− a olacak şekilde
1
mevcuttur. Burada belirtmek gerekir ki eğer max a1 , b−a
= a1 ise n > a1 >
1
b−a
olduğundan 1/n < a ve 1/n b−a
> a1 olduğundan 1/n < a ve 1/n 0 olduğundan ötürü E kümesi na
ile üstten sınırlıdır. Dolayısıyla k0 := sup E mevcuttur ve aynı zamanda Teorem
1.3.6’ye göre E kümesinin, özel olarak da N’nin bir elemanıdır. m = k0 + 1 ve
q = m/n olsun. k0 sayısı E kümesinin supremumu olduğundan m ∈
/ E’dir. Yani,
m/n > a sağlanır. Diğer taraftan k0 ∈ E olduğundan n sayısının seçiminden
ötürü
k0
k0
1
m
b = a + (b − a) ≥
+ (b − a) >
+ =
=q
n
n
n
n
ifadesi elde edilir. Yani a < q = m
n −a olacak şekilde bir k ∈ N
sayısı vardır. Bu eşitsizliğin her iki tarafına a eklenir ve a < b olduğu göz önüne
alınır ise 0 < k + a < k + b bulunur. Dolayısıyla, yukarıda ispatlandığı üzere
k + a < r < k + b olacak şekilde bir r ∈ Q sayısının varlığı garantidir. Buna
göre q := r − k sayısı Q rasyonel sayılar kümesinin elemanıdır ve a < q < b
eşitsizliğini gerçekler.
Tanım 1.3.10. E reel sayıların boştan farklı bir alt kümesi olsun. Buna göre
i) E kümesinin alttan sınırlı olarak adlandırılması için gerek ve yeter şart
her a ∈ E için a ≥ m olacak şekilde bir m ∈ R elemanının var olmasıdır.
Bu durumda m sayısına E kümesinin bir alt sınırı denir.
ii) Bir t sayısının E kümesinin inﬁmumu olarak adlandırılması için gerek
ve yeter şart t’in E kümesinin bir alt sınırı olması ve E’nin tüm m alt
sınırları için t ≥ m eşitsizliğinin gerçeklenmesidir. Bu durumda E kümesi
bir t inﬁmumuna sahiptir denir ve t = inf E yazılır.
iii) Bir E kümesinin sınırlı olarak adlandırılması için gerek ve yeter şart hem
alttan hem de üstten sınırlı olmasıdır.
22
Genellikle supremumunu içeren bir E kümesi için sup E yerine max E, inﬁmumunu içeren bir E kümesi için inf E yerine min E yazılır. Bazı yazarlar
supremumu üst sınırların en küçüğü, inﬁmumu alt sınırların en büyüğü olarak adlandırırlar. Fakat biz bu terminolojiyi en küçük üst sınır en büyük
alt sınırdan her zaman büyük veya eşit olacağından öğrencide bir karışıklık
yaratmaması bakımından kullanmayacağız.
İnﬁmum ve supremum arasındaki bağlantıyı ortaya koymak için yansıma
tanımını kullanırız. Bir E ⊆ R kümesinin yansıması
−E := {x : x = −a, a ∈ E}
olarak tanımlanır. Tanıma göre −(1, 2] = [−2, −1)’dir.
Aşağıdaki sonuç bir kümenin supremumunun, o kümenin yansımasının inﬁmumunun ters işaretli haline eşit olduğunu söyler. Bu sonuç kullanılarak inﬁmum için Yaklaşım Özelliği ve Tamlık Özelliği verilebilir (bkz Alıştırma 1.3.7).
Teorem 1.3.11 (Yansıma Prensibi). E ⊆ R kümesi boştan farklı olsun.
i) E kümesinin supremumu olabilmesi için gerek ve yeter şart
inf(−E) = − sup(E)
sağlayacak şekilde −E kümesinin bir inﬁmuma sahip olmasıdır.
ii) E kümesinin inﬁmumu olabilmesi için gerek ve yeter şart
sup(−E) = − inf(E)
sağlayacak şekilde −E kümesinin bir supremuma sahip olmasıdır.
Kanıt. i) ve ii) şıklarının kanıtları benzer olduğundan sadece ilk ifadenin ispatını vereceğiz.
E kümesinin supremumu s ve t = −s olsun. s sayısı E kümesinin bir üst
sınırı olduğundan her a ∈ E için s ≥ a yani −s = t ≤ −a eşitsizliği geçerlidir.
Buna göre t sayısı −E kümesi için bir alt sınırdır. −E kümesinin herhangi bir
alt sınırı m olsun. Her a ∈ E için m ≤ −a yani −m ≥ a gerçeklendiğinden −m
sayısı E kümesinin bir üst sınırıdır. E kümesinin supremumu s olduğundan
s ≤ −m yani t = −s ≥ m sağlanır. Bu ise t’nin −E kümesinin inﬁmumu
olduğu ve sup E = s = −t = − inf(−E) eşitliğinin sağlandığı anlamına gelir.
Tersine, −E kümesinin inﬁmumu t olsun ve inf(−E) = − sup(E) eşitliği
sağlansın. Tanıma göre her a ∈ E için t ≤ −a eşitsizliği geçerli olduğundan
−t sayısı E kümesinin bir üst sınırıdır. E kümesi boş olmadığından Tamlık
Aksiyomu gereği E kümesinin bir supremumu vardır.
Teorem 1.3.12 (Monotonluk Özelliği). R’nin boştan farklı A ⊆ B içermesini
gerçekleyen alt kümeleri verilsin.
23
i) Eğer B kümesinin supremumu varsa sup A ≤ sup B’dir.
ii) Eğer B kümesinin inﬁmumu varsa inf A ≥ inf B’dir.
Kanıt. i) A ⊆ B olduğundan B kümesine ait her üst sınır aynı zamanda A
kümesini de üstten sınırlar. Dolayısıyla sup B sayısı A’nın bir üst sınırıdır.
Buna göre Tamlık Aksiyomu gereği sup A mevcuttur ve Tanım 1.3.1 ii)’ye göre
sup A ≤ sup B eşitsizliği elde edilir.
ii) Açıkça A ⊆ B içermesi −A ⊆ −B olmasını gerektirir. Dolayısıyla i)
şıkkı, Teorem 1.3.11 ve İkinci Çarpma Özelliği göz önüne alındığında
inf A = − sup(−A) ≥ − sup(−B) = inf B
sonucu elde edilir.
Supremum ve inﬁmum tanımlarını R’nin tüm alt kümelerine uyarlamak
mümkündür. Bunu gerçekleştirmek içinSR’nin tanımını genişletmek gerekir.
Genişletilmiş reel sayılar kümesi R := R {±∞} olarak tanımlanır. Buna göre
bir x sayısının genişletilmiş reel sayılar kümesinin bir elemanı olabilmesi için
gerek ve yeter şart x ∈ R, x = +∞ veya x = −∞ ifadelerinden birinin gerçeklenmesidir.
Boştan farklı bir E ⊆ R kümesi göz önüne alınsın. Eğer E kümesi üstten
sınırlı değil ise sup E = +∞, alttan sınırlı değil ise inf E = −∞ olarak tanımlanır. Ayrıca sup ∅ = −∞ ve inf ∅ = +∞ şeklinde tanımlanır. Dikkat edilirse
R’nin bir E alt kümesinin supremumunun sonlu olabilmesi için gerek ve yeter
şart E’nin boştan farklı ve üstten sınırlı olmasıdır. Benzer şekilde bu E alt
kümesinin inﬁmumunun sonlu olabilmesi için gerek ve yeter şart E’nin boştan
farklı ve alttan sınırlı olmasıdır. Ayrıca, her a ∈ R için −∞ < a ve a < ∞
olduğu esasına göre Monotonluk Özelliği bu genişletilmiş tanım için de doğrudur. Yani −∞ < ∞ kuralı altında R’nin A ⊆ B içermesini sağlayan her A, B
alt kümeleri için sup A ≤ sup B ve inf A ≥ inf B eşitsizlikleri geçerlidir.
Alıştırmalar
1.3.1. Aşağıdaki ifadelerin hangilerinin doğru hangilerinin yanlış olduğunu belirleyiniz. Doğru olanları ispatlayıp yanlış olanlara ise ters örnek veriniz.
a) A ve B reel sayıların boştan farklı ve sınırlı iki alt kümesi ise sup(A∩B) ≤ sup A
sağlanır.
b) ε pozitif bir reel sayı olsun. A reel sayıların boştan farklı sınırlı bir alt kümesi
ve B = {xǫ : x ∈ A} ise sup B = ε sup A eşitliği gerçeklenir.
c) A ve B reel sayıların boştan farklı ve sınırlı iki alt kümesi olmak üzere A+B :=
{a + b : a ∈ A ve b ∈ B} şeklinde tanımlansın. Buna göre sup(A + B) =
sup(A) + sup(B) sağlanır.
d) A ve B reel sayıların boştan farklı ve sınırlı iki alt kümesi olmak üzere A−B :=
{a − b : a ∈ A ve b ∈ B} şeklinde tanımlansın. Buna göre sup(A − B) =
sup(A) − sup(B) sağlanır.
24
1.3.2. Aşağıda verilen her bir kümenin supremum ve inﬁmumunu tespit ediniz.
a)
b)
c)
d)
e)
f)
E
E
E
E
E
E
= {x ∈ R : x2 + 2x = 3}
= {x ∈ R : x2 − 2x + 3 > x2 ve x > 0}
= {p/q ∈ Q : p2 < 5q 2 ve p, q > 0}
= {x ∈ R : x = 1 + (−1)n /n, n ∈ N}
= {x ∈ R : x = 1/n + (−1)n , n ∈ N}
= {2 − (−1)n /n2 : n ∈ N}
1.3.3. Her a ∈ R ve n ∈ N için |a − rn | < 1/n olacak şekilde bir rn rasyonel sayısının
varlığını gösteriniz.
1.3.4. (İrrasyonel Sayıların Yoğunluğu) Gösteriniz ki a < b özelliğini gerçekleyen her
a, b reel sayısı için bir ξ ∈ R irrasyonel sayısı a < ξ < b eşitsizliğini sağlayacak şekilde
vardır.
1.3.5. Bir kümenin alt sınırının tek türlü belirli olmak zorunda olmadığını fakat
verilen bir E kümesinin inﬁmumunun tek türlü belirli olduğunu ispatlayınız.
1.3.6. Z’nin boştan farklı bir E alt kümesi için inf E’nin mevcut ve E kümesinin
elemanı olduğunu kanıtlayınız.
1.3.7. Yansıma Prensibi ve supremum için benzer sonuçları kullanarak aşağıdaki
ifadelerin doğruluğunu gösteriniz.
a) (İnﬁmum için Yaklaşım Özelliği) E ⊂ R kümesinin sonlu bir supremumu var
olsun. Buna göre ε > 0 herhangi bir pozitif sayı olmak üzere
inf E + ε > a ≥ inf E
eşitsizliğini gerçekleyen bir a ∈ E noktası vardır.
b) (İnﬁmum için Tamlık Özelliği) Eğer boştan farklı E ⊆ R kümesi alttan sınırlı
ise bir (sonlu) inﬁmumu vardır.
a) E ⊆ R kümesinin bir üst sınırı x ve x ∈ E ise gösteriniz ki E’nin
supremumu x sayısıdır.
b) Yukarıdaki ifadenin benzerini inﬁmum için tekrar yazıp ispatlayınız.
c) Örnek vererek yukarıdaki ifadelerin terslerinin doğru olmadığını gösteriniz.
1.3.8.
1.3.9. E, A, B ∈ R ve E = A ∪ B olsun. Gösteriniz ki eğer E’nin supremumu varsa
ve A, B kümeleri boştan farklı ise sup A ve sup B değerlerinin her ikisi de mevcuttur
ve sup E sayısı sup A veya sup B’den birine eşittir.
1.3.10. k, n ∈ Z olmak üzere k/2n formundaki bir sayıya diyadik rasyonel adı verilir.
a < b özelliğini sağlayan her a ve b reel sayıları için a < q < b eşitsizliğini gerçekleyen
bir q diyadik rasyonelinin varlığını gösteriniz.
1.3.11. xn ∈ R ve her n ∈ N için |xn | ≤ M olacak şekilde bir M ∈ R sayısı var olsun.
Gösteriniz ki her n ∈ N için sn = sup{xn , xn+1 , · · · } ifadesi bir reel sayı tanımlar
ve s1 ≥ s2 ≥ · · · eşitsizliği gerçeklenir. Benzer sonucu tn = inf{xn , xn+1 , · · · } için
ispatlayınız.
1.3.12. Eğer a, b ∈ R reel sayıları için b − a > 1 sağlanıyor ise a < k < b olacak
şekilde en az bir k ∈ Z sayısının varlığını gösteriniz.
25
1.4
Ters Fonksiyonlar ve Görüntüler
Kısım 1.1’den biliyoruz ki f : X → Y fonksiyonunun bir ters fonksiyonu olması
için gerek ve yeter şart Ran(f ) = Y ve her y ∈ Y elemanının tek türlü belirli
bir x ∈ X ön görüntüsüne sahip olmasıdır. Bu durumda f −1 ters fonksiyonu
f −1 (y) := x olarak tanımlanır. Özel olarak f : X → Y fonksiyonunun tersi
varsa her x ∈ X ve y ∈ Y için aşağıdaki ifadeler doğrudur:
f −1 (f (x)) = x ve
f (f −1 (y)) = y.
(1.10)
Teorem 1.4.1. X ve Y iki küme ve f : X → Y olsun. Buna göre aşağıda
verilen üç ifade birbirine denktir.
i) f ’in bir tersi vardır;
ii) f fonksiyonu X’den Y ’ye üzerine bire-bir bir fonksiyondur;
iii) Her x ∈ X ve y ∈ Y için bir g : Y → X fonksiyonu aşağıdaki iki koşulu
gerçekleyecek şekilde mevcuttur:
g(f (x)) = x
(1.11)
f (g(y)) = y.
(1.12)
ve
Ayrıca her f : X → Y için (1.11) ve (1.12) ifadelerini sağlayan sadece bir g
fonksiyonu vardır. Bu fonksiyon f −1 ters fonksiyonudur.
Kanıt. i) gerektirir ii). f fonksiyonunun bir tersi olsun. Tanım gereği Ran(f ) =
Y ’dir. Yani f fonksiyonu X’den Y ’ye üzerine bir fonksiyondur ve her y ∈ Y
elemanının tek türlü belirli bir x ∈ X ön görüntüsü vardır. Yani f (y1 ) = f (y2 )
için y1 = y2 sağlanır ki bu f ’in X üzerinde bire-bir olduğu anlamına gelir.
ii) gerektirir iii). f fonksiyonu X’den Y ’ye üzerine bire-bir bir fonksiyon
olsun. i) gerektirir ii) ispatı aynı zamanda f ’in bire-bir ve üzerine olması durumunda bir tersi olduğunu da söyler. Özel olarak g(y) := f −1 (y) fonksiyonu
(1.10)’den ötürü (1.11) ve (1.12) ifadelerini de gerçekler.
iii) gerektirir i). (1.11) ve (1.12) ifadelerini gerçekleyen bir g : Y → X fonksiyonu var olsun. Eğer bir y ∈ Y elemanının X içinde x1 , x2 gibi birbirinden
farklı iki ön görüntüsü varsa f (x1 ) = y = f (x2 ) yazılabilir. Bu durumda (1.11)’e
göre x1 = g(f (x1 )) = g(f (x2 )) = x2 olduğu sonucu elde edilir ki bu x1 6= x2
olması ile çelişir. Diğer taraftan verilen bir y ∈ Y için x = g(y) olsun. (1.12)’e
göre f (x) = f (g(y)) = y, yani Ran(f ) = Y olduğu sonucu elde edilir.
Son olarak, (1.11) ve (1.12) ifadelerinin her ikisini birden sağlayan bir başka
h fonksiyonunun olduğunu kabul edelim ve y ∈ Y elemanını sabitleyelim. ii)’ye
26
göre f (x) = y olacak şekilde bir x ∈ X vardır. Dolayısıyla (1.11)’den
h(y) = h(f (x)) = x = g(f (x)) = g(y)
ifadesi yazılabilir ki buna göre Y üzerinde h = g sağlanır. Yani g fonksiyonu
tek türlü belirlidir.
Biliyoruz ki bir f fonksiyonunun bire-bir olduğunu göstermek için iki yol
vardır. Ya f (x1 ) = f (x2 ) olduğu kabul edilip x1 = x2 eşitliğinin doğruluğu
gösterilmelidir ya da x1 6= x2 için f (x1 ) 6= f (x2 ) olduğu kanıtlanmalıdır. Eğer
X kümesi R içinde bir aralık ve f diferansiyellenebilir ise f ’in X üzerinde
bire-bir olduğunu göstermenin daha kolay bir yolu vardır.
Açıklama 1.4.2. I bir aralık ve f : I → R bir foksiyon olsun. Eğer f ’in türevi
I üzerinde her zaman pozitif ya da her zaman negatif değerler alıyor ise f
fonksiyonu I aralığı üzerinde bire-birdir.
Kanıt. Simetriden ötürü f ’in türevi olan f ′ fonksiyonunun her x ∈ X için
f ′ (x) > 0 koşulunu sağladığını, yani pozitif olduğunu farzedelim. Tek değişkenli
fonksiyonları daha önceden incelemiş olan herkes bilir ki bir I aralığında f ′ > 0
koşulunu sağlayan bir fonksiyon kesinlikle artandır. Yani x1 < x2 koşulunu
sağlayan x1 , x2 ∈ I için f (x1 ) < f (x2 ) gerçeklenir (bu özelliğin ispatı daha
sonra verilecektir).
Yukarıdaki özelliğin bire-bir olmayı neden gerektirdiğini göstermek için x1 ,
x2 ∈ X olmak üzere f (x1 ) = f (x2 ) eşitliğinin sağlandığını düşünelim. Eğer
x1 6= x2 ise Trikotami Özelliği gereği ya x1 < x2 ya da x2 < x1 ’dir. f fonksiyonu
I üzerinde kesinlikle artan olduğundan ya f (x1 ) < f (x2 ) ya da f (x2 ) < f (x1 )
sağlanır. Bu her iki durum da f (x1 ) = f (x2 ) olması varsayımı ile çelişir.
Teorem 1.4.1’e göre f : X → Y fonksiyonunun f −1 ters fonksiyonu olması
için gerek ve yeter şart her x ∈ X için f −1 (f (x)) = x ve her y ∈ Y için
f (f −1 (y)) = y eşitliklerinin sağlanmasıdır. Buna göre eğer y = f (x) fonksiyonu
x’e göre çözülebiliyorsa f −1 için bir formül bulunabilir.
Örnek 1.4.3. f (x) = ex − e−x fonksiyonunun R’de bire-bir olduğunu gösterip
Ran(f ) üzerinde f −1 için bir formül bulunuz.
Çözüm. Her x ∈ R için f ′ (x) = ex + e−x > 0 olduğundan Açıklama 1.4.2’ye
göre f fonksiyonu R üzerinde bire-birdir.
y = ex + e−x olsun. Bu ifadenin her iki tarafını ex ile çarpar, sıfırdan farklı
tüm terimleri bir tarafa toplarsak ex ’in
e2x − yex − 1 = 0
27
şeklinde kuadratik denklemini elde ederiz. İkinci derece denklemlerin çözümü
için bilinen formül kullanılarak
p
y ± y2 + 4
x
e =
(1.13)
2
sonucu elde edilir. ex ifadesi her zaman pozitif olduğundan negatif işaret göz
p
ardı edilmelidir. Son eşitlikten logaritma alınır ise x = log(y + y 2 + 4) − log 2
elde edilir ki bu ise
p
f −1 (x) = log(x + x2 + 4) − log 2
olduğu anlamına gelir.
Tanım 1.4.4. X ve Y iki küme f : X → Y olsun. Buna göre E ⊆ X kümesinin
f altındaki görüntüsü (veya imajı)
f (E) := {y ∈ Y : y = f (x) olacak şekilde x ∈ E vardır},
E ⊆ Y kümesinin f altındaki ters görüntüsü (veya ters imajı)
f −1 (E) := {x ∈ X : f (x) = y olacak şekilde y ∈ E vardır}
olarak tanımlanır.
f (E)
f
E
H
f
−1
(H)
E’nin bir aralık olması durumunda ekstra parantezleri ihmal ederiz. Örneğin
f ((a, b]) yerine f (a, b] ve f −1 ((a, b]) yerine f −1 (a, b] yazılabilir.
Örnek 1.4.5. f : R → R fonksiyonu f (x) = x2 olarak tanımlansın. Buna göre
E = {x : 0 ≤ x ≤ 2} kümesinin görüntüsü f (E) = {y : 0 ≤ y ≤ 4} kümesidir.
G = {y : 0 ≤ y ≤ 4} olsun. Buna göre G kümesinin f altındaki ters
görüntüsü f −1 (G) = {x : −2 ≤ x ≤ 2} kümesidir. Bu durumda f −1 (f (E)) 6= E
olduğu sonucu elde edilir.
Diğer taraftan f (f −1 (G)) = G eşitliği gerçeklenir. Fakat H = {y : −1 ≤
y ≤ 1} olması durumunda f (f −1 (H)) = {y : 0 ≤ y ≤ 1} =
6 H sonucu elde
edilir.
28
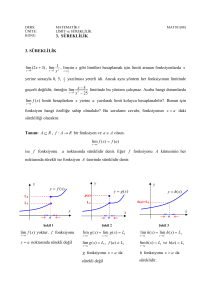
Örnek 1.4.6. f (x) = x2 + x fonksiyonu altında I = (−1, 0) ve J = (0, 1]
kümelerinin görüntülerini ve ters görüntülerini bulunuz.
Çözüm. “Bulmak” demek “ispatlamak” anlamına gelmediğinden y = x2 + x
fonksiyonunun graﬁğine bakarız.
Tanıma göre f (I) kümesi x’ler I = (−1, 0) aralığından değerler almak üzere
f (x)’in y-değerlerini içerir. f (x) = x2 + x = x(x + 1) fonksiyonunun x = 0, −1
noktalarında kökleri vardır ve x = −0.5 noktasında −0.25 minimum değerini
alır. Graﬁğe bakarak f (I) = [−0.25, 0) olduğu kolayca görülür. f −1 (I) kümesi görüntüsü I = (−1, 0) aralığına ait x-değerlerini içerdiğinden ve f fonksiyonunun graﬁği −1 < x < 0 için x-ekseninin altında yer aldığından açıkça
f −1 (I) = (−1, 0) olduğu görülür.
Benzer şekilde J = (0, 1] kümesinin görüntüsü f (J) = (0, 2] olmakla birlikte
[ −1 + √5 h −1 − √5
−1
.
, −1
0,
f (J) =
2
2
sonucu elde edilir.
DİKKAT. Ne yazık ki f −1 ’in üç tane anlamı bulunmaktadır: (1) f fonksiyonunun reel değerleri ve f (x) 6= 0 olması durumunda f −1 (x) = 1/f (x)
ters fonksiyonu; (2) f ’in bire-bir ve üzerine olması durumunda f −1 (x) ters
fonksiyonu; (3) f altında E’nin f −1 (E) ters görüntüsünü ifade etmede hep aynı
notasyon kullanılmaktadır. Metin içerisinde bunlardan hangisinin kast edildiği
anlaşılmalıdır.
29
Dikkat edilirse Tanım 1.4.4 bir asimetri içerir: y ∈ f (E) olması x ∈ E için
y = f (x) eşitliğinin sağlandığı anlamına gelir. Fakat x ∈ f −1 (E) olması y ∈ E
için x = f −1 (y) eşitliğinin sağlanacağı anlamına gelmez. Örneğin, f (x) = sin x
olsun. Her k ∈ Z için sin(kπ) = 0 olduğundan f altında {0} kümesinin ters
görüntüsü f −1 ({0}) = {kπ : k ∈ Z} olmakla birlikte arcsin x fonksiyonunun
değer bölgesi [−π/2, π/2] olduğundan {0}’ın f −1 altındaki imajı arcsin{0} =
{0}’dır.
Eğer göz önüne alınan kümelerin sayısı alfabenin harﬂerinden daha çok
değil ise onlar A, B, · · · , W gibi harﬂerle temsil edilebilir. Eğer alfabenin harflerinden daha çok ve sayıları n tane olan kümeler söz konusu ise bu kümeler A1 , A2 , · · · An simgeleri ile temsil edilebilir. Bu durumda, her bir Ai (i =
1, 2, 3, · · · , n) kümesi i ile indislenmiştir denir. Şimdi bu kavramı biraz daha
genelleştirelim. Herhangi bir A kümesini düşünelim. Her α ∈ A elemanına
karşılık bir Eα kümesi var olsun. Bütün bu kümelerden oluşan topluluk E ile
gösterilirse
E = {Eα : α ∈ A}
yazılabilir. Buna göre E topluluğu, elemanları Eα kümeleri olan bir kümedir.
Dolayısıyla E’ye bir kümeler ailesi veya kümeler topluluğu denir. Burada A
kümesine ailenin indis kümesi, her bir Eα kümesine α ile indislenmiş küme ve
her bir α ∈ A elemanına da bir indis adı verilir.
Yukarıda yapılan tanıma göre bir kümeler ailesinin bir A kümesi ile indislenmesi için gerek ve yeter şart A’dan E üzerine bir F fonksiyonunun var olmasıdır
(yani, her α ∈ A ile ilişkilendirilmiş E içerisinde bir ve yalnız bir küme vardır).
A ile indislenmiş E kümeler ailesi çoğunlukla E = {Eα }α∈A olarak gösterilir.
Tanım 1.4.7. E = {Eα }α∈A bir kümeler ailesi olsun.
i) Bir E kümeler ailesinin birleşimi
[
α∈A
Eα := {x : x ∈ Eα olacak şekilde α ∈ A vardır}
şeklinde tanımlanan kümedir. Yani bir x elemanının bu birleşime ait olabilmesi için gerek ve yeter şart en az bir α ∈ A için x ∈ Eα olmasıdır.
ii) Bir E kümeler ailesinin kesişimi
\
α∈A
Eα := {x : her α ∈ A için x ∈ Eα }
şeklinde tanımlanan kümedir. Yani bir x elemanının bu arakesite ait olabilmesi için gerek ve yeter şart her bir α ∈ A için x ∈ Eα olmasıdır.
Örneğin,
[
[0, x) = [0, 1)
ve
x∈(0,1]
\
[0, x) = {0}
x∈(0,1]
30
sağlanır.
Aşağıdaki önemli ve çokça kullanılan sonuç birleşimden keşisime ve tersi
geçişlerde kolay bir yol olduğunu göstermektedir.
Teorem 1.4.8 (DeMorgan Kuralları). X bir küme ve {Eα }α∈A ise X’in alt
kümelerinin bir ailesi olsun. Her E ⊆ X için E c ile X\E kümesi temsil edilmek
üzere
!c
\
[
=
Eαc
(1.14)
Eα
α∈A
α∈A
ve
\
α∈A
eşitlikleri geçerlidir.
Eα
!c
=
[
Eαc
(1.15)
α∈A
Kanıt. x elemanı (1.14) ifadesinin sol tarafında verilen kümeye ait olsun. Bu
S
durumda x ∈ X ve x ∈
/ α∈A Eα ifadeleri gerçeklenir. Tanıma göre x ∈ X ve
her α ∈ A için x ∈
/ Eα sağlanır. Dolayısıyla her α ∈ A için x ∈ Eαc gerçeklenir.
Bu ise x’in (1.14) ifadesinin sağ tarafında verilen kümeye ait olduğu anlamına
gelir. Bu adımlar terslenebilir olduğundan (1.14) eşitliğinin sağlandığı görülür.
Benzer şekilde hareket ederek (1.15) ifadesinin doğruluğu elde edilir.
Aşağıdaki sonuç kümelerin birleşim ve kesişimlerinin görüntü ve ters görüntüleri hakkında yorum yapmamızı sağlaması bakımından önemlidir.
Teorem 1.4.9. X ve Y iki küme, f : X → Y olsun.
i) X’in alt kümelerinin bir ailesi {Eα }α∈A ise
!
!
[
\
[
\
f
f (Eα ) ve f
f (Eα )
Eα =
Eα ⊆
α∈A
α∈A
α∈A
α∈A
ifadeleri doğrudur.
ii) X’in herhangi iki B ve C alt kümeleri için
f (C\B) ⊇ f (C)\f (B)
içermesi gerçeklenir.
iii) Y ’nin alt kümelerinin bir ailesi {Eα }α∈A ise
!
[
[
f −1
f −1 (Eα ) ve f −1
Eα =
α∈A
α∈A
ifadeleri doğrudur.
31
\
α∈A
Eα
!
=
\
α∈A
f (Eα )
iv) Y ’nin herhangi iki B ve C alt kümeleri için
f −1 (C\B) = f −1 (C)\f −1 (B)
eşitliği gerçeklenir.
v) Eğer E ⊆ f (X) ise f (f −1 (E)) = E gerçeklenir. Diğer taraftan, E ⊆ X
ise f −1 (f (E)) ⊇ E içermesi doğrudur.
Kanıt. i) Tanıma göre y ∈ f (∪α∈A Eα ) ifadesinin sağlanması için gerek ve yeter şart x ∈ Eα ve α ∈ A için y = f (x) eşitliğinin gerçeklenmesidir. Bu ise
y ∈ ∪α∈A f (Eα ) olmasına denktir. Benzer şekilde, y ∈ f (∩α∈A Eα ) ifadesinin
sağlanması için gerek ve yeter şart x ∈ ∩α∈A Eα için y = f (x) eşitliğinin gerçeklenmesidir. Buna göre her α ∈ A için y = f (xα ) olacak şekilde bir xα ∈ Eα
elemanı vardır. Dolayısıyla, y ∈ ∩α∈A f (Eα ) olduğu sonucu elde edilir.
ii) Eğer y ∈ f (C)\f (B) ise c ∈ C için y = f (c) ve her b ∈ B için y 6= f (b)
gerçeklenir. Dolayısıyla, y ∈ f (C\B) sağlanır. Benzer şekilde hareket ederek
iii), iv) ve v) ifadelerinin doğruluğu gösterilebilir.
i), ii) ve v) şıklarında verilen içermelerde f fonksiyonunun bire-bir olmaması
durumunda eşitlik halinin hiçbir zaman gerçeklenmeyeceğini görmek önemlidir
(bkz Alıştırma 1.4.7 ve 1.4.8). Örneğin, eğer f (x) = x2 , E1 = {1} ve E2 = {−1}
ise f (E1 ∩ E2 ) = ∅ kümesi f (E1 ) ∩ f (E2 ) = {1} kümesinin bir alt kümesidir.
Alıştırmalar
1.4.1. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu
tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) f (x) = sin x olsun. Bu durumda
π 3π
f:
,
→ [−1, 1]
2 2
fonksiyonu bir bijeksiyondur ve ters fonksiyonu arcsin x’dir.
b) A, B, C verilen bir X kümesinin alt kümeleri olmak üzere f : X → X fonksiyonu
tanımlansın. Eğer A ∩ B 6= ∅ ise f (A) ∩ f (B ∪ C) 6= ∅ sağlanır.
c) A ve B verilen bir X kümesinin alt kümeleri olsun. Buna göre (A\B)c = B\A
eşitliği geçerlidir.
d) Eğer f fonksiyonu [−1, 1] aralığını [−1, 1] üzerine resmediyor ise f −1 (f ({0})) =
{0} sağlanır.
1.4.2.
a) Aşağıda verilen f fonksiyonlarının E üzerinde bire-bir olduklarını gösterip f (E) kümesini tespit ediniz.
i) f (x) = 3x − 7, E = R
ii) f (x) = e1/x , E = (0, ∞)
32
iii)
iv)
v)
vi)
f (x) = tan x, E = (π/2, 3π/2)
f (x) = x2 + 2x − 5, E = (−∞, −6)
f (x) = 3x − |x| + |x + 2|, E = R
f (x) = x/(x2 + 1), E = [−1, 1]
b) f (E) üzerinde f −1 için bir açık formül bulunuz.
1.4.3. Aşağıda verilen ifadelerin her biri için f (E) ve f −1 (E) kümelerini teşkil ediniz.
a)
b)
c)
d)
e)
f (x) = 2 − 3x, E = (−1, 2)
f (x) = x2 + 1, E = (−1, 2]
f (x) = 2x − x2 , E = [−2, 2)
f (x) = log(x2 − 2x + 1), E = (0, 3]
f (x) = cos x, E = [0, ∞)
1.4.4. Aşağıdaki şekilde tanımlanan her bir küme için basit bir tanımlama yapınız.
S
a) x∈[0,1] [x − 2, x + 1]
T
b) x∈[0,1] (x − 1, x + 1]
T
c) k∈N − k1 , k1
S
d) k∈N − k1 , 0
S
e) k∈N −k, k1
T
f) k∈N k−1
, k+1
k
k
1.4.5. (1.15) ifadesini ispatlayınız.
1.4.6. Teorem 1.4.9 iii), iv) ve v) şıklarının doğruluğunu gösteriniz.
1.4.7. f (x) = x2 olsun.
a) R’nin f (C\B) 6= f (C)\f (B) eşitsizliğini gerçekleyen iki B ve C alt kümelerini
bulunuz.
b) R’nin f −1 (f (E)) 6= f (E) eşitsizliğini gerçekleyen bir E alt kümesini bulunuz.
1.4.8. X ve Y iki küme ve f : X → Y olsun. Aşağıdaki ifadelerin birbirine denk
olduğunu gösteriniz.
a)
b)
c)
d)
f fonksiyonu X üzerinde bire-birdir.
X’in her A ve B alt kümesi için f (A\B) = f (C)\f (B) eşitliği sağlanır.
X’in her E alt kümesi için f −1 (f (E)) = E’dir.
X’in her A ve B alt kümesi için f (A ∩ B) = f (A) ∩ f (B) ifadesi doğrudur.
33
2 Reel Değerli Diziler
2.1
Dizilerin Limitleri
Bir sonsuz dizi (ya da kısaca dizi ) tanım bölgesi N doğal sayılar olan bir fonksiyondur. Terimleri xn := f (n) olan bir f dizisi x1 , x2 , x3 , · · · veya {xn }n∈N veya
{xn }∞
n=1 veya {xn } şeklinde gösterilebilir. Buna göre 1, 1/2, 1/4, 1/8, · · · ifadesi
{1/2n−1 }n∈N dizisini; −1, 1, −1, 1, · · · ifadesi {(−1)n }n∈N dizisini; ve 1, 2, 3, · · ·
ifadesi ise {n}n∈N dizisini temsil eder.
Tamamen iki ayrı konsepte sahip {xn }n∈N dizisi ile {xn : n ∈ N} kümesini birbirine karıştırmamak gerekir. Örneğin, dizi olarak göz önüne alındığında 1, 2, 3, 4, · · · ile 2, 1, 3, 4, · · · birbirlerinden farklıdırlar. Fakat küme anlamında {1, 2, 3, 4, · · · } ile {2, 1, 3, 4, · · · } kümeleri özdeştirler. Diğer taraftan
1, −1, 1, −1, · · · sonsuz bir dizi iken {(−1)n : n ∈ N} kümesinin sadece iki tane
elemanı vardır.
Limit kavramı analizin temel taşlarından birisidir. Temel matematik derslerinden biliyoruz ki bir {xn } reel sayı dizisinin bir a sayısına yakınsaması için
n sayısı büyüdükçe xn değerlerinin a’ya yaklaşması (yani a ile xn arasındaki
mesafenin kısalması) gerekir. Dolayısıyla, verilen bir ε > 0 için (ne kadar küçük
olduğunun önemi olmaksızın), eğer n sayısı yeterince büyük ise, |xn − a| farklı
ε’dan küçüktür. Buna göre bir dizinin limiti için aşağıdaki biçimsel tanım verilebilir:
Tanım 2.1.1. Reel sayıların bir {xn } dizisinin bir a ∈ R reel sayısına yakınsaması için gerek ve yeter şart her ε > 0 sayısına karşılık
her n ≥ N için |xn − a| < ε
olacak şekilde bir N ∈ N (genellikle ε’a bağlı) sayısının var olmasıdır.
Aşağıdaki ifadeler ve notasyonlar sıkça birbirinin yerine kullanılır:
a) {xn } dizisi a’ya yakınsar; b) xn dizisi a’ya yakınsar; c) a = limn→∞ xn ;
d) n → ∞ iken xn → a; e) {xn } dizisinin limiti vardır ve a sayısına eşittir.
n → ∞ iken xn → a ifadesinde, xn dizisini a değerine yapılan yaklaşımların
bir dizisi ve ε değerini ise bu yaklaşımda oluşan hata için bir üst sınır olarak
düşünmek mümkündür. Tanım 2.1.1’deki N değeri n ≥ N için hata değeri
ε’dan küçük olacak şekilde seçilir.
a−ε
x1
x3
(
a+ε
x5 . . . a . . . x6
)
x4
x2
Tanımdan anlaşılacağı üzere xn dizisinin a değerine yakınsaması için gerek
ve yeter şart n → ∞ iken |xn − a| → 0 olmasıdır. Özel olarak xn → 0 olması
için gerek ve yeter şart n → ∞ iken |xn | → 0 sağlanmasıdır.
Tanım 2.1.1’e göre belirli bir limitin varlığını göstermek için öncelikle ne
kadar küçük olduğu önemli olmayan verilen bir ε > 0 sayısına karşılık n ≥ N
için |xn − a| < ε eşitsizliğini gerçekleyecek N sayısının ne şekilde seçileceğini
tanımlamak gerekir. Özellikle, ε sayısı N belirlenmeden tanımlanır ve N sayısı
genellikle ε’a bağlıdır. Her n ≥ N için |xn − a| < ε sağlandığından N sayısı n’e
bağlı olamaz.
Limitin varlığı ile ilgili somut örneklere geçmeden önce bir terminoloji daha
verelim. Pn ifadesi N ile indislenmiş bir özelliği göstersin. Her n ≥ N için
Pn özelliğinin doğru olduğu bir N ∈ N sayısı varsa büyük n değerleri için Pn
gerçeklenir denir. Dolayısıyla, Tanım 2.1.1’in bir informal özeti xn dizisinin
a değerine yakınsaması için gerek ve yeter şart n sayısı büyük olmak üzere
|xn −a| farkının küçük olmasıdır şeklinde verilebilir. Bu ifadenin anlamı, verilen
bir pozitif ε (ne kadar küçük olduğunun önemi olmaksızın) sayısına karşılık her
n ≥ N için |xn − a| farkı ε’dan küçük olacak şekilde yeterince büyük bir N
doğal sayısının seçilebileceğidir.
Örnek 2.1.2.
i) n → ∞ iken 1/n → 0 olduğunu ispatlayınız.
ii) xn → 2 ise n → ∞ iken (2xn + 1)/xn → 5/2 olduğunu gösteriniz.
iii) limn→∞ n21+1 = 0 olduğunu gösteriniz.
iv) limn→∞ 3n+2
n+1 = 3 olduğunu ispatlayınız.
Çözüm. i) ε > 0 olsun. Archimedean Özelliği kullanılarak N > 1ε olacak şekilde bir N ∈ N sayısı seçilsin. Bu eşitsizliğin tersi alındığında n ≥ N olmak
üzere 1/n ≤ 1/N < ε ifadesi elde edilir. 1/n oranının tüm değerleri pozitif
olduğundan her n ≥ N için |1/n| < ε eşitsizliğine ulaşılır. Buna göre n → ∞
iken 1/n → 0 sağlanır.
ii) için Strateji: Tanıma göre gösterilmesi gereken büyük n değerleri için
2xn + 1 5
2 − xn
− =
xn
2
2xn
ifadesinin küçük olduğudur. Bu son yazılan kesrin payının değeri n → ∞ iken
xn → 2 olduğundan büyük n değerleri için küçük olacaktır. Peki payda için ne
söylenebilir? xn → 2 olduğundan büyük n değerleri için xn değeri 1’den büyük
olacaktır. Dolayısıyla, büyük n için 2xn değeri 2’den büyük olacaktır. n değerini iki kere büyüttüğümüzden Tanım 2.1.1’de verilen ε değerine karşılık gelen
36
N sayısını belirlemede iki kısıtlama yapmamız gerekir. Tüm bu kısıtlamalar
altında aşağıdaki çözümü verebiliriz:
ii) ε > 0 olsun. xn → 2 olduğundan Tanım 2.1.1’e göre ε > 0 sayısına
karşılık n ≥ N1 için |xn − 2| < ε olacak şekilde bir N1 ∈ N sayısı vardır. Şimdi,
ε = 1 olmak üzere Tanım 2.1.1’i uygulayarak n ≥ N2 için |xn − 2| < 1 olacak
şekilde bir N2 sayısı seçelim. Mutlak Değerin Temel Teoremi’nden n ≥ N2 için
−1 < xn − 2 < 1 yani xn > 1, dolayısıyla 2xn > 2 olduğu sonucu elde edilir.
N = max{N1 , N2 } seçilsin ve n ≥ N olsun. n ≥ N1 olduğundan |2 − xn | =
|xn −2| < ε sağlanır. Diğer taraftan n ≥ N2 olduğundan 0 ≤ 1/(2xn ) < 1/2 < 1
eşitsizliği elde edilir. Buna göre her n ≥ N için
2xn + 1 5 |2 − xn |
ε
=
−
<
<ε
xn
2
2xn
2xn
olduğu sonucuna ulaşılır.
iii) ε > 0 sayısı verilsin. N sayısını bulmak için n ∈ N olmak üzere
1
1
1
< 2 ≤
n2 + 1
n
n
eşitsizliğini kullanırız. i) şıkkında olduğu gibi ε > 0 olduğundan 1/ε > 0’dir
ve Archimedean Özelliği’ne göre bir N = N (ε) doğal sayısı (burada N (ε) ile
N doğal sayısının ε’a bağlı olduğu ifade edilmektedir) 1/N < ε olacak şekilde
mevcuttur. Buna göre n ≥ N olması 1/n < ε eşitsizliğinin sağlandığı anlamına
gelir ve buradan
1
1
1
=
−
0
n2 + 1 < n < ε
n2 + 1
elde edilir. Yani, verilen dizinin limiti sıfırdır.
iii) ε > 0 sayısı verilsin. Yeterince büyük n için
3n + 2
n + 1 − 3 < ε
(2.1)
eşitsizliğinin sağlandığının gösterilmesi gerekmektedir. Öncelikle yukarıda verilen ifadenin sol tarafını sade halde yazalım:
3n + 2
3n + 2 − 3n − 3 −1 1
1
=
=
−
3
n+1
n + 1 = n + 1 < n.
n+1
Buna göre eğer 1/n < ε ifadesi gerçeklenir ise (2.1) eşitsizliği sağlanır. Archimedean Özelliği yukarıda anlatıldığı şekilde aynen uygulandığında aranan N
sayısının varlığı ve verilen dizinin limitinin 3 olduğu kolayca gösterilebilir. 37
Örnek 2.1.2 ii)’de dikkat edilirse N sayısı N1 ve N2 ’nin maksimumu olacak şekilde seçildi. Bu seçim bize n ≥ Nj (j = 1, 2) için maksimum olma
özelliğinden n ≥ N eşitsizliğinin sağlanmasını garantiler. Benzer şekilde, her j
için n ≥ Nj için N1 , N2 , · · · , Nq sayıları bir Pj özelliğini gerçeklesin. Eğer N =
max{N1 , N2 , · · · , Nq } ise tüm q değerleri için n ≥ N olmak üzere P1 , P2 , · · · , Pq
özellikleri aynı anda gerçeklenir. Bu olgu yapılan ispatlarda sıkça kullanılmakla
birlikte N değerinin Nj tamsayılarının maksimumu olduğu açık olarak kimi durumlarda belirtilmemektedir.
Aşağıdaki iki sonuç bir dizinin ya limiti olmadığını ya da tektürlü belirli bir
limiti olduğunu gösterir.
Örnek 2.1.3. {(−1)n }n∈N dizisinin limiti yoktur.
Çözüm. a ∈ R için n → ∞ iken (−1)n → a olsun. Buna göre verilen ε = 1 için
bir N ∈ N sayısı n ≥ N olmak üzere |(−1)n − a| < ε eşitsizliğini sağlayacak
şekilde mevcuttur. n sayısının tek olması durumunda |1 + a| = | − 1 − a| < 1
ve n’nin çift olması dırımında ise |1 − a| < 1 sağlanır. Buna göre
2 = |1 + 1| ≤ |1 − a| + |1 + a| < 1 + 1 < 2
yani 2 < 2 çelişkisi elde edilir. Dolayısıyla {(−1)n }n∈N dizisinin bir limiti yoktur.
Açıklama 2.1.4. Bir dizi en fazla bir limit değerine sahip olabilir.
Kanıt. {xn } dizisi a ve b değerlerine yakınsasın. Tanıma göre verilen bir ε > 0
sayısına karşılık her n ≥ N için |xn − a| < ε/2 ve |xn − b| < ε/2 eşitsizliklerini
sağlayacak şekilde bir N ∈ N tamsayısı mevcuttur. Buna göre, üçgen eşitsizliği
kullanılarak
|a − b| = |a − b + xn − xn | ≤ |xn − a| + |xn − b| < ε
ifadesi elde edilir. Yani her ε > 0 sayısı için |a − b| < ε eşitsizliği sağlanır. Bu
ise Teorem 1.2.9’ya göre a = b olmasını gerektirir.
Tanım 2.1.5. Bir {xn }n∈N dizisi verilsin. Her nk ∈ N için n1 < n2 < · · ·
özelliğini sağlayan {xnk } dizisine {xn } dizisinin bir alt dizi si adı verilir.
Tanıma göre x1 , x2 , · · · şeklindeki bir dizinin xn1 , xn2 , · · · alt dizisi x1 , x2 , · · ·
dizisinden n = nk eşitliğini sağlayan indisler hariç tüm xn ’lerin atılması ile elde
edilir. Örneğin 1, 1, · · · dizisi özel olarak (−1)n dizisinin nk = 2k eşitliğini sağlayan terimler hariç diğer tüm terimlerinin silinmesi ile elde edilmiş bir alt dizidir.
Benzer şekilde, 1/2, 1/4, · · · dizisi özel olarak 1/n dizisinin nk = 2k özelliğini
sağlayan terimler hariç diğer tüm terimlerinin silinmesi ile elde edilmiş bir alt
dizisidir.
38
Görüldüğü üzere {1/n} dizisi, bir alt dizisi olan {1/2n } dizisine göre limit
değeri olan sıfıra çok daha yavaş yakınsar. Diğer taraftan Örnek 2.1.3’te gösterildiği gibi {(−1)n } dizisinin bir limiti yok iken bu dizinin bir alt dizisi olan
1, 1, · · · dizisi 1’e yakınsar.
Eğer n → ∞ iken xn → a ise n büyüdükçe xn değerlerinin a’ya yaklaştığı
söylenebilir. k büyüdükçe nk değeri de büyüyeceğinden yakınsak bir dizinin
herhangi bir alt dizisinin de yakınsak olacağı sonucu sezilebilir.
Açıklama 2.1.6. a değerine yakınsayan bir {xn }n∈N dizisi verilsin ve bu
{xn }n∈N dizisinin herhangi bir {xnk }n∈N alt dizisi göz önüne alınsın. Buna
göre k → ∞ için xnk değerleri de a’ya yakınsar.
Kanıt. ε > 0 olsun ve n ≥ N için |xn − a| < ε eşitsizliğini sağlayan N ∈ N
seçilsin. nk ∈ N ve n1 < n2 < · · · olduğundan her k ∈ N için nk ≥ k gerçeklenir.
Dolayısıyla, k ≥ N için |xnk − a| < ε sağlanır. Buna göre k → ∞ iken xnk → a
olduğu sonucu elde edilir.
Aşağıdaki tanım dizi teorisi içerisinde oldukça önemli bir yere sahiptir.
Tanım 2.1.7. Reel sayıların bir {xn } dizisi verilsin.
i) {xn } dizisinin üstten sınırlı olarak adlandırılması için gerek ve yeter şart
{xn : n ∈ N} kümesinin üstten sınırlı olmasıdır.
ii) {xn } dizisinin alttan sınırlı olarak adlandırılması için gerek ve yeter şart
{xn : n ∈ N} kümesinin alttan sınırlı olmasıdır.
iii) {xn } dizisinin sınırlı olarak adlandırılması için gerek ve yeter şart bu
dizinin üstten ve alttan sınırlı olmasıdır.
Tanım 2.1.7 ve Tanım 1.3.1 birlikte düşünüldüğünde {xn } dizisinin üstten
sınırlı olması için gerek ve yeter şart her n ∈ N için xn ≤ M olacak şekilde
bir M ∈ R sayısının var olmasıdır. Benzer şekilde {xn } dizisinin alttan sınırlı
olması için gerek ve yeter şart her n ∈ N için xn ≥ m olacak şekilde bir m ∈ R
sayısının var olmasıdır. Diğer taraftan açık olarak {xn } dizisinin sınırlı olması
için gerek ve yeter şart her n ∈ N için |xn | ≤ C olacak şekilde bir C > 0
sayısının var olmasıdır (bkz Alıştırma 2.1.5). Bu durumda {xn } dizisi C ile
sınırlıdır veya domine edilmiştir denir.
Yakınsak ve sınırlı diziler arasında aşağıdaki önemli ilişki mevcuttur.
Teorem 2.1.8. Her yakınsak dizi sınırlıdır.
Strateji: n → ∞ iken xn → a olsun. Tanıma göre yeterince büyük N için
xN , xN +1 , · · · değerleri a’ya yakın olmalıdır. Bu ise sınırlılığı gerektirir. Ayrıca
x1 , · · · , xN −1 sonlu dizisi de sınırlı olduğundan verilen dizi sınırlıdır.
39
Kanıt. limn→∞ xn = a olsun. Buna göre, verilen ε = 1 sayısına karşılık n ≥ N
için |xn − a| < 1 olacak şekilde bir N ∈ N sayısı vardır. Dolayısıyla, üçgen
eşitsizliği kullanılarak her n ≥ N için |xn |−|a| ≤ |xn −a| < 1 yani |xn | < 1+|a|
ifadesi elde edilir. Diğer taraftan, 1 ≤ n ≤ N için
|xn | ≤ M := max{|x1 |, |x2 |, · · · , |xN |}
olduğundan {xn } dizisinin max{M, 1 + |a|} ile domine edildiği sonucu elde
edilir.
Örnek 2.1.3 göz önüne alındığında Teorem 2.1.8’in tersinin doğru olmadığı
sonucu elde edilir.
Yakınsak Dizi ⇒ Sınırlı Dizi, Sınırlı Dizi ; Yakınsak Dizi
Alıştırmalar
2.1.1. Aşağıdaki ifadelerin hangilerinin doğru hangilerinin yanlış olduğunu belirleyiniz. Doğru olanları ispatlayıp yanlış olanlara ise ters örnek veriniz.
a)
b)
c)
d)
xn
xn
xn
xn
yakınsak ise xn /n dizisi de yakınsaktır.
yakınsak değil ise xn /n dizisi de yakınsak değildir.
yakınsak ve yn sınırlı ise xn yn dizisi yakınsaktır.
dizisi sıfıra yakınsıyor ve her n ∈ N için yn > 0 ise xn yn dizisi de yakınsaktır.
2.1.2. Aşağıdaki limitlerin varlığını Örnek 2.1.2i), iii), iv)’de anlatılan metodu kullanarak gösteriniz.
a)
b)
c)
d)
n→∞
n→∞
n→∞
n→∞
iken
iken
iken
iken
2 − 1/n → 2.
√
1 + π/ n → 1.
3(1 + 1/n) → 3.
(2n2 + 1)/(3n2 ) → 2/3.
2.1.3. Reel sayıların n → ∞ iken 1’e yakınsayan bir xn dizisi göz önüne alınsın.
Tanım 2.1.1 kullanılarak aşağıdaki limitlerin varlığını ispatlayınız.
a) limn→∞ (1 + 2xn ) = 3.
b) limn→∞ (πxn − 2)/(xn ) = π − 2.
c) limn→∞ (x2n − e)/xn = 1 − e.
2.1.4. Aşağıda verilen her bir diziye ait farklı limitlere sahip iki yakınsak alt dizi
bulunuz.
a) 3 − (−1)n .
b) (−1)3n + 2.
c) (n − (−1)n n − 1)/n.
2.1.5. xn ∈ R olsun.
a) {xn } dizisinin sınırlı olması için gerek ve yeter şart her n ∈ N için |xn | ≤ C
olacak şekilde bir C > 0 sayısının var olmasıdır
40
b) {xn } dizisi sınırlı olsun. Buna göre her k ∈ N için n → ∞ iken xn /nk → 0
olduğunu gösteriniz.
2.1.6. C bir pozitif sabit olsun. {bn } negatif olmayan sayıların sıfıra yakınsayan bir
dizisi ve {xn } yeterince büyük n değerleri için |xn − a| < Cbn özelliğini sağlayan reel
sayıların bir dizisi ise xn ’in a’ya yakınsadığını ispatlayınız.
2.1.7. a bir reel sabit olmak üzere n ∈ N için xn := a olarak tanımlansın. Buna göre
{xn } “sabit” dizisinin yakınsak olduğunu ispatlayınız.
a) {xn } ve {yn } dizileri aynı bir reel sayıya yakınsasınlar. Buna göre n →
∞ iken xn − yn → 0 olduğunu gösteriniz.
b) {n} dizisinin yakınsamadığını ispatlayınız.
c) a) şıkkının hükmünü gerçekleyen sınırsız xn 6= yn dizilerinin varlığını gösteriniz.
2.1.8.
2.1.9. {xn } reel sayıların bir dizisi olsun. xn dizisinin a değerine yakınsaması için
gerek ve yeter şartın xn ’nin HER alt dizisinin a’ya yakınsaması olduğunu ispatlayınız.
2.2
Limit Teoremleri
Hem teoride hem de uygulamada karşılaşılan en büyük problemlerden birisi
verilen bir dizinin yakınsak olduğu olmadığıdır. Eğer verilen dizinin yakınsak
olduğu biliniyorsa limit değerine farklı teknikler kullanılarak yaklaşımda bulunulabilir veya bu limit hesaplanabilir.
Teorem 2.2.1 (Sıkıştırma Teoremi). {xn }, {yn } ve {wn } reel sayı dizileri
olsun.
i) Eğer n → ∞ iken xn → a ve yn → a (AYNI a değeri) ve
n ≥ N0 için xn ≤ wn ≤ yn
eşitliği sağlanacak şekilde bir N0 ∈ N var ise bu durumda n → ∞ iken
wn → a sağlanır.
ii) Eğer n → ∞ iken xn → 0 ve {yn } dizisi sınırlı ise n → ∞ iken xn yn → 0.
Kanıt. i) ε > 0 olsun. xn ve yn dizileri a değerine yakınsadığından Tanım 2.1.1
ve Teorem 1.2.6 kullanılarak n ≥ N1 için −ε < xn − a < ε ve n ≥ N2 için −ε <
yn −a < ε eşitsizliklerini sağlayan N1 , N2 ∈ N seçilebilir. N = max{N0 , N1 , N2 }
olsun. n ≥ N için teorem hipotezine ve N1 ve N2 ’nin seçiminden
a − ε < x n ≤ wn ≤ yn < a + ε
eşitsizliği sağlanır. Buna göre n ≥ N için |wn − a| < ε olduğu elde edilir.
Dolayısıyla n → ∞ için wn → a sonucuna ulaşılır.
41
ii) xn → 0 ve n ∈ N için |yn | ≤ M olacak şekilde bir M > 0 sayısı var
olsun. ε > 0 olmak üzere |xn | < ε/M eşitsizliğini n ≥ N için sağlayacak şekilde
N ∈ N seçilsin. Buna göre n ≥ N için
|xn yn | < M
ε
=ε
M
sağlanır. Yani n → ∞ iken xn yn → 0 gerçeklenir.
Aşağıdaki Sıkıştırma Teoremi’nin ne şekilde kullanıldığına ilişkin bir örnek
verilmektedir.
Örnek 2.2.2. limn→∞ 2−n cos(n3 − n2 + n − 13) limit değerini bulunuz.
Çözüm. Her x ∈ R için | cos x| ≤ 1 olduğu kullanılırsa {2−n cos(n3 − n2 + n −
13)} dizisinin 2−n ile domine edildiği sonucuna ulaşılır. Diğer taraftan 2n > n
olduğundan 2−n < n1 ’dir. Buna göre Örnek 2.1.2 i) ve Sıkıştırma Teoremi’ne
göre n → ∞ iken n1 → 0 olduğundan 2−n → 0 dolayısıyla 2−n cos(n3 − n2 +
n − 13) → 0 limit değeri elde edilir.
Teorem 2.2.3. E ⊂ R olsun. Eğer E kümesinin sonlu bir supremumu varsa
n → ∞ iken xn → sup E olacak şekilde bir xn ∈ E dizisi vardır. Benzer şekilde,
eğer E kümesinin sonlu bir inﬁmumu varsa n → ∞ iken yn → inf E olacak
şekilde bir yn ∈ E dizisi vardır.
Kanıt. E kümesinin sonlu bir supremumu olsun. Buna göre Supremum için
Yaklaşım Özelliği’ne göre sup E − n1 < xn ≤ sup E eşitsizliğini sağlayacak
şekilde bir xn ∈ E vardır. Dolayısıyla, Sakıştırma Teoremi ve Örnek 2.1.2 i)’ye
göre n → ∞ iken xn → sup E sağlanır. Benzer şekilde n → ∞ iken yn → inf E
olacak şekilde bir yn ∈ E dizisinin varlığı gösterilebilir.
Teorem 2.2.4. {xn } ve {yn } iki reel sayı dizisi ve α ∈ R olsun. Eğer {xn } ve
{yn } yakınsak ise
i) limn→∞ (xn + yn ) = limn→∞ xn + limn→∞ yn ,
ii) limn→∞ (αxn ) = α limn→∞ xn ,
ve
iii) limn→∞ (xn yn ) = (limn→∞ xn ) (limn→∞ yn )
eşitlikleri gerçeklenir. Bunlara ek olarak yn 6= 0 ve limn→∞ yn 6= 0 ise
iv) limn→∞
xn
yn
=
limn→∞ xn
limn→∞ yn
ifadesi gerçeklenir ve özellikle tüm bu limitler mevcuttur.
42
Kanıt. limn→∞ xn = x ve limn→∞ yn = y olsun.
i) ε > 0 olsun ve n ≥ N için |xn − x| < ε/2 ve |yn − y| < ε/2 eşitsizliklerini
sağlayacak şekilde N ∈ N seçilsin. Buna göre üçgen eşitsizliği kullanılarak n ≥
N için
ε ε
|(xn + yn ) − (x + y)| ≤ |xn − x| + |yn − y| < + = ε
2 2
elde edilir. Yani, n → ∞ iken (xn + yn ) → (x + y) sağlanır.
ii) n → ∞ iken αxn − αx → 0 olduğunu göstermek yeter. n → ∞ iken
xn − x → 0 olduğundan Sıkıştırma Teoremi’ne göre n → ∞ iken α(xn − x) → 0
sonucu elde edilir. Yani, limn→∞ (αxn ) = αx eşitliği bulunur.
iii) Teorem 2.1.8’e göre her yakınsak dizi sınırlı olduğundan yakınsak {xn }
dizisi sınırlıdır. Dolayısıyla Sıkıştırma Teoremi’ne göre {xn {yn − y}} ve {{xn −
x}y} dizilerinin her ikisi de 0 değerine yakınsar. Diğer taraftan
xn yn − xy = xn (yn − y) + (xn − y)y
olduğundan i) şıkkına göre n → ∞ iken xn yn → xy olduğu sonucu elde edilir.
Benzer argüman kullanılarak iv) ifadesinin gerçeklendiği gösterilebilir.
Örnek 2.2.5. limn→∞ (n3 + n2 − 1)/(1 − 3n3 ) limitini hesaplayınız.
Çözüm. Verilen ifadenin pay ve paydasını 1/n3 ile çarparsak
n3 + n2 − 1
1 + (1/n) − (1/n3 )
=
1 − 3n3
(1/n3 ) − 3
elde edilir. Örnek 2.1.2 i) ve Teorem 2.2.4 iii) göz önüne alındığında her k ∈ N
için n → ∞ iken 1/nk (1/n)k → 0 olduğu sonucuna ulaşılır. Dolayısıyla Teorem
2.2.4 i), ii) ve iv) şıklarına göre
1+0−0
1
n3 + n2 − 1
=
=−
n→∞
1 − 3n3
0−3
3
lim
limit değeri bulunur.
Tanım 2.2.6. {xn } reel sayıların bir dizisi olsun.
i) {xn } dizisinin +∞’a ıraksıyor (notasyon: n → ∞ iken xn → +∞ ya
da limn→∞ xn = +∞) olarak adlandırılması için gerek ve yeter şart her
M ∈ R için n ≥ N olmak üzere xn > M eşitsizliğini sağlayacak bir N ∈ N
sayısının var olmasıdır.
ii) {xn } dizisinin −∞’a ıraksıyor (notasyon: n → ∞ iken xn → −∞ ya
da limn→∞ xn = −∞) olarak adlandırılması için gerek ve yeter şart her
M ∈ R için n ≥ N olmak üzere xn < M eşitsizliğini sağlayacak bir N ∈ N
sayısının var olmasıdır.
43
Sıkıştırma Teoremi sonsuz limitlere genişletilebilir. Aşağıdaki sonuç Teorem
2.2.4’ün bir genişletilmesidir.
Teorem 2.2.7. {xn } ve {yn } iki reel sayı dizisi olsun öyleki n → ∞ iken
xn → +∞ (sırası ile, xn → −∞) gerçeklensin.
i) Eğer yn alttan sınırlı (sırası ile, yn üstten sınırlı) ise
(sırası ile, lim (xn + yn ) = −∞).
lim (xn + yn ) = +∞
n→∞
n→∞
ii) Eğer α > 0 ise
(sırası ile, lim (αxn ) = −∞).
lim (αxn ) = +∞
n→∞
n→∞
iii) Eğer bir M0 > 0 ve her n ∈ N için yn > M0 ise
(sırası ile, lim (xn yn ) = −∞).
lim (xn yn ) = +∞
n→∞
n→∞
iv) Eğer {yn } sınırlı ve xn 6= 0 ise
lim
n→∞
xn
= 0.
yn
Kanıt. Kolaylık sağlaması bakımından limn→∞ xn = +∞ olsun.
i) Hipotez koşulu gereği yn alttan sınırlı olduğundan bir M0 ∈ R için yn ≥
M0 sağlanır. M ∈ R ve M1 = M − M0 olsun. xn → +∞ olduğundan n ≥ N
için xn > M1 eşitsizliğini sağlayacak şekilde bir N ∈ N sayısı vardır. Buna göre
n ≥ N için xn +yn > M1 +M0 = M gerçeklenir. Bu ise limn→∞ (xn +yn ) = +∞
olduğu anlamına gelir.
ii) M ∈ R ve M1 = M/α olsun. xn → +∞ olduğundan n ≥ N için xn > M1
eşitsizliğini sağlayacak şekilde bir N ∈ N sayısı vardır. Buna göre α > 0 olmak
üzere her n ≥ N için αxn > αM1 = M gerçeklenir. Bu ise limn→∞ (αxn ) = +∞
olduğu anlamına gelir.
iii) M ∈ R ve M1 = M/M0 olsun. xn → +∞ olduğundan n ≥ N için
xn > M1 eşitsizliğini sağlayacak şekilde bir N ∈ N sayısı vardır. Ayrıca hipotez
koşulu gereği n ∈ N için yn > M0 olduğundan n ≥ N için xn yn > M1 M0 = M
elde edilir. Bu ise limn→∞ (xn yn ) = +∞ olduğu anlamına gelir.
iv) ε > 0 olsun. {yn } sınırlı olduğundan |yn | ≤ M0 eşitsizliğini sağlayacak
şekilde bir M0 > 0 sayısı vardır. Diğer taraftan M0 /M1 < ε olacak şekilde bir
M1 > 0 sayısı seçilsin. Ayrıca, xn → +∞ olduğundan n ≥ N için xn > M1
eşitsizliğini sağlayacak şekilde bir N ∈ N sayısı vardır. Tüm bu seçimler altında
n ≥ N için
yn |yn |
M0
=
<
<ε
xn xn
M1
eşitsizliğ gerçeklenir. Bu ise limn→∞ xynn = 0 olduğu anlamına gelir.
44
Eğer aşağıdaki kuralları kabul edersek
x ∈ R için
x > 0 için
x < 0 için
x + ∞ = ∞,
x · ∞ = ∞,
x − ∞ = −∞
x · (−∞) = −∞
x · ∞ = −∞, x · (−∞) = ∞
∞ · ∞ = (−∞) · (−∞) = ∞
∞ · (−∞) = (−∞) · (∞) = −∞
Teorem 2.2.7’nin Sonuç 2.2.8’i içerir.
Sonuç 2.2.8. {xn } ve {yn } reel sayı dizileri, α, x ve y genişletilmiş reel sayılar
olsun. n → ∞ iken xn → x ve yn → y ise aşağıdaki ifadenin sağ tarafının
∞ − ∞’dan farklı olma koşulu altında
lim (xn + yn ) = x + y
n→∞
sağlanır. Ayrıca bundan fazla olarak aşağıdaki ifadenin sağ tarafının 0·±∞’dan
farklı olma koşulu altında
lim (αxn ) = αx,
lim (xn yn ) = xy
n→∞
n→∞
gerçeklenir.
Dikkat edilirse ∞ − ∞ ve 0 · ±∞ durumlarından uzak durulmaktadır.
Çünkü bu formlar “belirsiz”dir. Belirsizlik hallerinin incelemesi ileriki derslerde
l’Hôpital Kuralı ile verilecektir.
Teorem 2.2.4 ve Teorem 2.2.7’de limit işleminin R’nin cebirsel yapısı ile
ne şekilde etkileşime girdiği ortaya konmaktadır (Bir toplamın limiti (çarpımı,
bölümü) limitlerin toplamı (çarpımı, bölümü) olarak yazılabilir). Aşağıdaki teorem limit işleminin R’nin bir diğer yapısı üzerindeki etkileşimini işaret etmektedir.
Teorem 2.2.9 (Karşılaştırma Teoremi). {xn } ve {yn } yakınsak diziler olsun.
Eğer
n ≥ N0 için xn ≤ yn
(2.2)
eşitsizliğini sağlayan bir N0 ∈ N sayısı varsa
lim xn ≤ lim yn
n→∞
n→∞
eşitsizliği sağlanır. Özel olarak, eğer xn ∈ [a, b] dizisi bir c noktasına yakınsıyor
ise bu c sayısı [a, b] aralığında olmalıdır.
45
Kanıt. Teoremin ifadesinin yanlış olduğunu kabul edelim. Yani, (2.2) sağlanırken x := limn→∞ xn limit değeri y := limn→∞ yn limit değerinden büyük olsun.
ε = (x − y)/2 verilsin. Buna göre n ≥ N1 için |xn − x| < ε ve |yn − y| < ε
olacak şekilde bir N1 > N0 seçilebilir. Dolayısıyla bu n sayısı için
x−y
x−y
=y+
= y + ε > yn
xn > x − ε = x −
2
2
sağlanır. Bu ise (2.2) ile çelişir. Dolayısıyla teoremde yer alan ilk ifadenin doğruluğu gösterilmiş olur.
a ≤ xn ≤ b olduğundan yukarıda elde edilen sonuç kullanılarak a ≤ c ≤ b
eşitsizliğinin sağlandığı görülür.
Yukarıdaki teoremi hatırlamanın bir yolu, söz konusu limitlerin varlığının
garantisi altında, bir eşitsizliğin limitinin, limitlerin eşitsizliği olduğudur. Bu
prosedür “verilen eşitsizliğin limitini almak” şeklinde isimlendirilir. xn < yn
eşitsizliğinden xn ≤ yn olduğu anlaşılacağından Karşılaştırma Teoremi şu sonucu içerir: Eğer {xn } ve {yn } yakınsak reel sayı dizileri ise
n ≥ N0 için xn < yn ise lim xn ≤ lim yn olduğu anlamına gelir.
n→∞
n→∞
Burada dikkat edilmesi gereken bir husus ≤ işaretinin < ile değiştirilmesi durumunda elde edilecek sonucun doğru olmadığıdır. Yani
n ≥ N0 için xn < yn ise lim xn < lim yn olduğu anlamına GELMEZ.
n→∞
n→∞
Örneğin, 1/n2 < 1/n olmasına karşın bu dizilerin limitleri eşittir.
Alıştırmalar
2.2.1. Aşağıdaki ifadelerin hangilerinin doğru hangilerinin yanlış olduğunu belirleyiniz. Doğru olanları ispatlayıp yanlış olanlara ise ters örnek veriniz.
a)
b)
c)
d)
n→∞
n→∞
n→∞
n→∞
iken
iken
iken
iken
xn
xn
xn
xn
→ ∞ ve xn → −∞ ise xn + yn → 0 sağlanır.
→ −∞ ise 1/xn → 0 sağlanır.
→ 0 ise 1/xn → ∞ sağlanır.
→ ∞ ise (1/2)xn → 0 sağlanır.
2.2.2. Aşağıdaki dizilerin sıfıra yakınsadığını ispatlayınız.
a)
b)
c)
d)
xn
xn
xn
xn
2
= sin(log n + n5 + en )/n
2
= 2n/(n
+ π)
√
√
= ( 2n + 1)/(n + 2)
n
= n/2
2.2.3. Tanım 2.2.6’yı kullanarak aşağıdaki ifadelerin +∞ veya −∞ değerlerine ıraksadığını gösteriniz.
a) xn = n2 − n
46
b) xn = n − 3n2
c) xn = (n2 + 1)/n
d) xn = n2 (2 + sin(n3 + n + 1))
2.2.4. Eğer varsa, aşağıdaki dizilerin limitlerini hesaplayınız.
a)
b)
c)
d)
xn
xn
xn
xn
= (2 + 3n − 4n2 )/(1 − 2n + 3n2 )
3
=√
(n3 + n − 2)/(2n
+ n − 2)
√
= √3n + 2 − √n
√
√
= ( 4n + 1 − n − 1)/( 9n + 1 − n + 2)
2.2.5.
a) Teorem 2.2.4 iv) ifadesini ispatlayınız.
b) Sonuç 2.2.8 ifadesini ispatlayınız.
2.2.6. x ∈ R ve xn ≥ 0 olmak üzere n → ∞ iken xn → x sağlansın. Buna göre
√
√
limn→∞ xn = x olduğunu ispatlayınız.
2.2.7. Verilen x ∈ R sayısına karşılık n → ∞ iken rn → ∞ olacak şekilde bir rn ∈ Q
dizisinin varlığını gösteriniz.
2.2.8. x ve y genişletilmiş reel sayılar, {xn }, {yn } ve {wn } reel sayı dizileri olsun.
a) [R için Sıkıştırma Teoremi] Eğer n → ∞ iken xn → x, yn → x ve n ∈ N
için xn ≤ wn ≤ yn eşitliği sağlanıyor ise bu durumda n → ∞ iken wn → x
gerçeklenir.
b) [R için Karşılaştırma Teoremi] Eğer n → ∞ iken xn → x, yn → x ve n ∈ N için
xn ≤ yn eşitliği sağlanıyor ise bu durumda x ≤ y gerçeklenir.
2.2.9. Alıştırma 2.2.6’yı kullanarak aşağıdaki ifadelerin doğru olduğunu ispatlayınız.
√
a) 0 ≤ x1 ≤ 1 ve n ∈ N için xn+1 = 1 − 1 − xn olsun. Eğer limn→∞ xn = x ise
x = 0 ya da 1’dir.
√
b) x1 > 3 ve n ∈ N için xn+1 = 2 + xn − 2 olsun. Eğer limn→∞ xn = x ise
x = 3’tür.
√
c) x1 ≥ 0 ve n ∈ N için xn+1 = 2 + xn olsun. Eğer limn→∞ xn = x ise x = 2’dir.
x1 > −2 olması durumunu inceleyiniz.
2.2.10.
a) n ≥ 0 için 0 ≤ y < 1/10n olsun. Buna göre
w
w
1
≤ y < n+1 + n+1
10n+1
10
10
eşitsizliğini sağlayacak şekilde bir 0 ≤ w ≤ 9 tamsayısının varlığını gösteriniz.
b) Verilen bir x ∈ [0, 1) sayısısına karşılık her n ∈ N için
n
n
X
X
1
xk
xk
≤x<
+ n
k
10
10k
10
k=1
k=1
eşitsizliğini sağlayacak şekilde 0 ≤ xk ≤ 9 tamsayılarının varlığını gösteriniz.
c) Verilen bir x ∈ [0, 1) sayısısına karşılık her k ∈ N için
n
X
xk
n→∞
10k
x = lim
k=1
eşitsizliğini sağlayacak şekilde 0 ≤ xk ≤ 9 tamsayılarının varlığını gösteriniz.
d) c) şıkkını kullanarak 0.5 = 0.4999 · · · ve 1 = 0.999 · · · olduğunu ispatlayınız.
47
2.3
Bolzano-Weierstrass Teoremi
Her ne kadar {(−1)n } dizisi yakınsak olmasa da, yakınsak bir alt diziye sahip
olduğunu biliyoruz. Bu bölümde, bu olgu ile alakalı genel bir kaide ispatlanacaktır. Bolzano-Weierstrass Teoremi adı verilen ve her sınırlı dizinin yakınsak
bir alt diziye sahip olduğunu belirten bu prensibi en genel halde ele almadan
önce söz konusu teoremin aşıkar olarak gerçeklendiği monotonluk kavramını
ortaya koyalım:
Tanım 2.3.1. Reel sayıların bir {xn }n∈N dizisi göz önüne alınsın.
i) {xn } dizisinin artan (sırası ile, kesinlikle artan) olarak isimlendirilmesi
için gerek ve yeter şart x1 ≤ x2 ≤ · · · (sırası ile, x1 < x2 < · · · ) eşitsizliğinin gerçeklenmesidir.
ii) {xn } dizisinin azalan (sırası ile, kesinlikle azalan) olarak isimlendirilmesi
için gerek ve yeter şart x1 ≥ x2 ≥ · · · (sırası ile, x1 > x2 > · · · ) eşitsizliğinin gerçeklenmesidir.
iii) {xn } dizisinin monoton olarak isimlendirilmesi için gerek ve yeter şart
dizinin artan veya azalan olmasıdır.
Bazı kaynaklarda azalan dizi yerine artmayan ve artan dizi yerine de azalmayan terimleri kullanılmaktadır.
Eğer {xn } dizisi artan (sırası ile, azalan) ise ve bir a değerine yakınsıyorsa
n → ∞ iken xn ↑ a (sırası ile, xn ↓ a) yazılacaktır. Açık olarak, kesinlikle artan
her dizi artandır ve kesinlikle azalan her dizi azalandır. Ayrıca, {xn } dizisinin
artan olması için gerek ve yeter şart {−xn } dizisinin azalan olmasıdır.
Teorem 2.1.8’e göre her yakınsak dizi sınırlıdır. Şimdi bu sonucun tersini
monoton diziler için kanıtlayalım.
Teorem 2.3.2 (Monoton Yakınsaklık Teoremi). Eğer {xn } dizisi artan ve
üstten sınırlı veya {xn } dizisi azalan ve alttan sınırlı ise {xn } sonlu bir limit
değerine yakınsar.
Kanıt. {xn } dizisi artan ve üstten sınırlı olsun. Tamlık Aksiyomu gereği sonlu
bir a := sup{xn : n ∈ N} supremumu vardır. ε > 0 olsun. Supremum için
Yaklaşım Özelliği kullanılarak
a − ε < xN ≤ a
olacak şekilde bir N ∈ N seçilsin. Dizi monoton artan olduğundan n ≥ N için
xN ≤ xn sağlanır. Ayrıca a verilen dizinin supremumu, dolayısıyla bir üst sınırı
olduğundan her n ∈ N için xn ≤ a gerçeklenir. Buna göre her n ≥ N için
a − ε < xN ≤ xn ≤ a < a + ε yani a − ε < xn ≤ a + ε eşitsizliği elde edilir.
48
Dolayısıyla n ≥ N için |xn − a| ≤ ε sağlanır. ε > 0 herhangi bir pozitif reel
sayı olduğundan {xn } dizisinin a’ya yakınsadığı sonucu elde edilir. Özel olarak,
{xn } artan olduğundan n → ∞ iken xn ↑ a yazılır.
{xn } dizisi azalan, alttan sınırlı ve b := inf{xn : n ∈ N} olsun. Buna göre
{−xn } dizisi artandır ve supremumu −b’dir (bkz Teorem 1.3.11). Yukarıda
verilen ilk durumdan ve Teorem 2.2.4 ii)’ye göre
b = −(−b) = − lim (−xn ) = lim xn
n→∞
n→∞
elde edilir.
Monoton Yakınsaklık Teoremi genellikle verilen bir dizinin limitinin varlığının gösterilmesi için kullanılır. Limitin varlığı bir kere gösterildiğinde Teorem
2.2.1 ve Teorem 2.2.4 kullanılarak bu limitin değerinin bulunması kolaydır.
Aşağıdaki örnek bu durumu ortaya koymaktadır.
Örnek 2.3.3. Eğer |a| < 1 ise n → ∞ iken an → 0’dır.
Çözüm. limn→∞ |a|n = 0 olduğunu göstermek yeterlidir. |a|n ifadesi Çarpma
Özelliği’ne göre monoton azalandır ve |a| < 1 olduğundan her n ∈ N için
|a|n+1 < |a|n sağlanır. Ayrıca mutlak değerin özelliğinden dolayı |a|n dizisi alttan (0 ile) sınırlıdır. Monoton azalan ve alttan sınırlı bir dizinin Monoton Yakınsaklık Teoremi’ne göre L := limn→∞ |a|n limiti mevcuttur. |a|n+1 = |a||a|n
cebirsel özdeşliğinin n → ∞ için limiti alınırsa Açıklama 2.1.6 ve Teorem 2.2.4’e
göre L = |a| · L olduğu sonucu elde edilir ki bu ise ya L = 0 ya da |a| = 1 demektir. Teorem hipotezine göre |a| < 1 eşitsizliği sağlandığından L = 0 olmak
zorundadır.
Örnek 2.3.4. Eğer a > 0 ise n → ∞ iken a1/n → 1’dir.
Çözüm. Problemi üç durumda ele alalım:
Durum 1. a = 1 olsun. Her n ∈ N için a1/n = 1 olduğundan n → ∞ iken
a1/n → 1 limit değeri elde edilir.
Durum 2. a > 1 olsun. Bu durumda Monoton Yakınsaklık Teoremi’ni kullanmak için {a1/n } dizisinin azalan ve alttan sınırlı olduğunu göstermek gerekir.
Bir n ∈ N sabitlensin. a > 1 olduğundan an+1 > an sağlanır. Bu eşitsizliğin her
iki tarafının n(n + 1). kökü alınırsa a1/n > a1/(n+1) sonucu elde edilir. Buna
göre a1/n azalandır. a > 1 olduğundan a1/n > 1 gerçeklenir ki bu ise a1/n
dizisinin alttan sınırlı olduğu anlamına gelir. Alttan sınırlı monoton azalan bir
dizinin Monoton Yakınsaklık Teoremi gereği L := limn→∞ a1/n limiti mevcuttur. Limit değerini bulmak için n → ∞ iken (a1/(2n) )2 = a1/n özdeşliğinin
her iki tarafının limitini alırsak L2 = L olduğu sonucu elde edilir. Buna göre
49
L = 0 ya da 1’dir. a1/n > 1 olduğundan Karşılaştırma Teoremi’ne göre L ≥ 1
sağlanacağından L = 1 olduğu sonucuna ulaşılır.
Durum 3. 0 < a < 1 olsun. Buna göre 1/a > 1’dir. Dolayısıyla Teorem 2.2.4 ve
Durum 2’den
lim a1/n = lim
n→∞
n→∞
1
1
=
=1
1/a1/n
limn→∞ (1/a)1/n
sonucu elde edilir.
Tanım 2.3.5. Bir {In }n∈N kümeler dizisinin iç içe geçmiş olarak isimlendirilmiş olması için gerek ve yeter şart
I1 ⊇ I2 ⊇ · · ·
şeklinde yazılabilmesidir.
Teorem 2.3.6 (İç İçe Geçmiş Aralık Özelliği). Eğer {In }n∈N boştan farklı kaT∞
palı sınırlı aralıkların iç içe geçmiş bir dizisi ise E := n=1 In boştan farklıdır.
Ayrıca, n → ∞ için bu aralıkların uzunlukları |In | → 0 oluyor ise E tek bir
noktadır.
Kanıt. In = [an , bn ] olsun. {In } iç içe geçmiş olduğundan {an } reel sayı dizisi
artandır ve üstten b1 ile sınırlıdır. Benzer şekilde {bn } dizisi azalandır ve alttan
a1 ile sınırlıdır. Dolayısıyla, Teorem 2.3.2’a göre n → ∞ iken an ↑ a ve bn ↓ b
olacak şekilde a, b ∈ R sayıları vardır. Her n ∈ N için an ≤ bn olduğundan
Karşılaştırma Teoremi’ne göre an ≤ a ≤ b ≤ bn sağlanır. Buna göre, bir x
sayısının her n ∈ N için In aralığına ait olması için gerek ve yeter şart a ≤ x ≤ b
eşitsiliğinin sağlanması, yani x ∈ [a, b] olmasıdır. Özel olarak, [a, b] aralığında
yer alan her x, aynı zamanda tüm In aralıklarına aittir.
a1
a2
a3
a4 . . . a
b . . . b4
b3
b2
b1
İspatın şimdiye kadar yapılan kısmında gösterildi ki tüm In ’lere ait tam olarak
bir elemanın varlığı için gerek ve yeter şart a = b eşitliğinin sağlanmasıdır.
Fakat, n → ∞ iken |In | → 0 olması demek bn − an → 0 anlamına gelir.
Dolayısıyla, Teorem 2.2.4’e göre n → ∞ iken |In | → 0 ise a sayısı b’ye eşittir.
50
Açıklama 2.3.7. İç İçe Geçmiş Aralık Özelliği’nde göz önüne alınan aralıkların
“kapalı” olma durumu ihmal edildiğinde Teorem 2.3.6 doğru olmayabilir.
Kanıt. Her n ∈ N için In = (0, 1/n) şeklinde tanımlanan aralıklar sınırlı ve iç
içe geçmiş olmakla birlikte kapalı değillerdir. Eğer her n ∈ N için bir x ∈ In
elemanı var olsaydı 0 < x < 1/n, yani her n ∈ N için n < 1/x sağlanırdı. Bu
ise Archimedean Özelliği ile çelişir. Buna göre In aralıkları ortak bir noktaya
sahip olamaz.
Açıklama 2.3.8. İç İçe Geçmiş Aralık Özelliği’nde göz önüne alınan aralıkların
“sınırlı” olma durumu ihmal edildiğinde Teorem 2.3.6 doğru olmayabilir.
Kanıt. n ∈ N olmak üzere In = [n, ∞) şeklinde tanımlanan kapalı ve iç içe
geçmiş sınırlı olmayan aralıklara ait ortak bir nokta yoktur.
Teorem 2.3.9 (Bolzano-Weierstrass Teoremi). Reel sayıların her sınırlı dizisi
yakınsak bir alt diziye sahiptir.
Strateji: Göstermemiz gereken {xn } dizisinin bir limit değerine yakınsayan
bir alt dizisinin olduğunur. Bunun için iç içe geçmiş In aralıkları kullanılacaktır. Özel olarak bu In aralıklarının uzunlukları n → ∞ iken 0’a yaklaşacak
şekilde seçilecektir. Bu seçimden ötürü aralıklar bir noktaya yaklaşacaktır. Bu
aşamada her bir adımda seçilen iç içe geçmiş aralığın verilen dizinin sonsuz sayıda terimini içerdiğinden emin olunması gerekir. Daha sonra her bir aralıktan
bir terim seçilerek yakınsak bir dizi formu elde edilecektir.
Kanıt. İspata genel bir gözlem ile başlayalım. {xn } herhangi bir dizi olsun.
Eğer A ve B kümelerinin birleşimi E = A ∪ B kümesi, n’nin sonsuz sayıda
değeri için xn içeriyor ise A veya B kümelerinin en az biri n’nin sonsuz sayıda
değeri için xn değerlerini içerir (Eğer içermeseydi bu durumda E kümesi, n’nin
sonlu sayıda değeri için xn sayılarını içerirdi ki bu ise çelişkiye neden olurdu).
{xn } reel sayıların herhangi sınırlı bir dizi olduğundan her n doğal sayısı
için |xn | ≤ C olacak şekilde bir C > 0 reel sayısı vardır. I1 = [a1 , b1 ] = [−C, C]
olsun. Sınırlılıktan ötürü her n ∈ N için a1 ≤ xn ≤ b1 olacak şekilde bir [a1 , b1 ]
aralığı vardır. I1 aralığı iki yarı-aralığa bölünsün ve c1 = (a1 + b1 )/2 denilsin.
Yukarıda anlatılanlardan ötürü [a1 , c1 ] veya [c1 , b1 ] aralıklarından (en az) biri
{xn } dizisinin sonsuz sayıdaki terimini içerir. Genelliği bozmadan [a1 , c1 ] kapalı
aralığının verilen dizinin sonsuz sayıda terimini içerdiği farz edilsin ve a2 =
a1 ve b2 = c1 olarak isimlendirilsin. Buna göre I2 = [a2 , b2 ] aralığında {xn }
dizisinin sonsuz sayıda terimi mevcuttur.
Yukarıdaki prosedürü tekrarlayarak I2 = [a2 , b2 ] aralığı iki eşit yarı-aralığa
2
denilsin. Buna göre bu yarı-aralıklardan (en az) birisi,
bölünsün ve c2 = a2 +b
2
51
[a2 , c2 ] veya [c2 , b2 ] aralığı, {xn } dizisinin sonsuz sayıda terimini içerecektir. Bu
özelliğe sahip olan aralık seçilsin ve I3 = [a3 , b3 ] olarak isimlendirilsin.
Benzer şekilde elde edilen In = [an , bn ] iç içe geçmiş aralıkları, {xn } dizisinin
sonsuz sayıda terimini içerecek şekilde teşkil edilsin. İç İçe Geçmiş Aralık Özelliği’nden a = limn→∞ an ve b = limn→∞ bn limitlerinin var olduğunu biliyoruz.
Diğer taraftan, [a1 , b1 ] = [−C, C] aralığının uzunluğu |I1 | = 2C, [a2 , b2 ] aralığının uzunluğu |I2 | = 2C/2 = C, [a3 , b3 ] aralığının uzunluğu |I3 | = 2C/22 =
C/2 ve genel olarak [an , bn ] aralığının uzunluğu |In | = C/2n−1 olduğundan
limn→∞ (bn − an ) = 0 yani a = b’dir.
I1 aralığı {xn } dizisinin en az bir xn1 terimini içerir. I2 aralığı {xn } dizisinin
sonsuz sayıda terimini içerdiğinden n2 > n1 özelliğini sağlayacak şekilde I2
aralığından bir xn2 seçilsin. Benzer şekilde, I3 aralığı {xn } dizisinin sonsuz
sayıda terimini içerdiğinden n3 > n2 > n1 özelliğini sağlayacak şekilde I3
aralığından bir xn3 terimi seçilsin. Bu prosedüre tekrar edilerek a değerine
yakınsayan {xn } dizisinin bir {xnk } alt dizisini elde edilir.
Alıştırmalar
2.3.1. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu
tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) xn kesinlikle azalan ve 0 ≤ xn < 1/2 ise n → ∞ iken xn → 0 sağlanır.
b) Eğer
(n − 1) cos(n2 + n + 1)
xn =
2n − 1
ise xn ’nin yakınsak bir alt dizisi vardır.
c) Eğer xn kesinkile artan bir dizi ve her n = 1, 2, 3 · · · için
|xn | < 1 +
1
n
ise limn→∞ xn = 1 gerçeklenir.
d) Eğer xn dizisinin yakınsak bir alt dizisi varsa, xn sınırlıdır.
√
2.3.2. x0 ∈ (−1, 0) ve n ∈ N için xn = xn−1 + 1 − 1 olsun. Buna göre n → ∞ iken
xn ↑ 0 olduğunu ispatlayınız. x0 ∈ [0, 1] olması durumu için yorum yapınız.
√
2.3.3. 0 ≤ x1 < 1 ve n ∈ N için xn+1 = 1 − 1 − xn olsun. Buna göre n → ∞ iken
xn ↓ 0 ve n → ∞ iken xn+1 /xn → 1/2 olduğunu gösteriniz.
√
2.3.4. x0 ≥ 2 ve n ∈ N için xn = 2 + xn−1 − 2 olsun. Monoton Yakınsaklık
Teoremi’ni kullanarak n → ∞ iken ya xn → 2 ya da xn → 3 olduğunu gösteriniz.
2.3.5. x0 ∈ R ve n ∈ N için xn = (1+xn−1 )/2 olsun. Monoton Yakınsaklık Teoremi’ni
kullanarak n → ∞ iken xn → 1 olduğunu gösteriniz.
52
2.3.6. Aşağıdaki limit değerlerinin doğruluğunu gösteriniz:
lim x
1/(2n−1)
n→∞


1


= 0



−1
x>0
x=0
x < 0.
a) {xn } reel sayıların monoton artan bir dizisi olsun (üstten sınırlı olmasına
gerek olmaksızın). n → ∞ iken xn → x olacak şekilde bir x genişletilmiş reel
sayısının varlığını gösteriniz.
b) Yukarıdaki özelliği azalan diziler için ifade edip ve ispatlayınız.
2.3.7.
2.3.8. E ⊂ R boştan farklı sınırlı bir küme olsun ve sup E ∈
/ E sağlansın. Her n ∈ N
için xn ∈ E olacak şekilde kesinlikle artan ve sup E değerine yakınsayan bir {xn }
dizisinin varlığını gösteriniz.
2.3.9. 0 < y1 < x1 olsun ve n ∈ N için
xn+1 =
√
xn + yn
ve yn+1 = xn yn
2
olarak tanımlansın.
a) Her n ∈ N için 0 < yn < xn olduğunu gösteriniz.
b) yn dizisinin artan ve üstten sınırlı, xn dizisinin azalan ve alttan sınırlı olduğunu
ispatlayınız.
c) n ∈ N için 0 < xn+1 − yn+1 < (x1 − y1 )/2n olduğunu gösteriniz.
d) limn→∞ xn = limn→∞ yn olduğunu gösteriniz (Bu ortak değere x1 ve y1 ’in
aritmetik-geometrik ortalaması adı verilir).
2.3.10. x0 = 1 ve y0 = 0 olsun ve n ∈ N için
xn = xn−1 + 2yn−1 ve yn = xn−1 + yn−1
olarak tanımlansın. Buna göre n ∈ N için x2n − 2yn2 = ±1 ve
√
xn
→ 2
n → ∞ iken
yn
olduğunu gösteriniz.
√
2.3.11. (Archimedes) x0 = 2 3 ve y0 = 3 olsun ve n ∈ N için
xn =
√
2xn−1 yn−1
ve yn = xn yn−1
xn−1 + yn+1
olarak tanımlansın.
a) n → ∞ iken x, y ∈ R için xn ↓ x ve yn ↑ y olduğunu gösteriniz.
b) x = y ve
3.14155 < x < 3.14161
olduğunu gösteriniz (x’in gerçek değeri π’dir).
53
2.4
Cauchy Dizileri
Bu bölümde oldukça etkili ve fazlaca kullanılan bir olgu üzerinde durulacaktır.
Tanıma göre, eğer {xn } yakınsak bir dizi ise büyük n değerleri için xn
terimlerinin yakınında yer alacağı bir a ∈ R noktası vardır. Eğer xn ’ler a’nın
yakınında ise doğal olarak birbirlerine de yakındırlar. Buna göre aşağıdaki konsept ortaya çıkar.
Tanım 2.4.1. xn ∈ R noktalar dizisinin (R’de) bir Cauchy dizisi olarak isimlendirilmesi için gerek ve yeter şart her ε > 0 sayısına karşılık
n, m ≥ N için |xn − xm | < ε
(2.3)
olacak şekilde bir N ∈ N doğal sayısının var olmasıdır.
o∞
n
dizisinin bir Cauchy dizisi olduğunu tanımı kullaÖrnek 2.4.2. 3n−7
9n+2
n=1
narak gösteriniz.
Çözüm. Gösterilmesi gereken her ε > 0 sayısına karşılık bir N pozitif tamsayısının n, m ≥ N için
3n − 7 3m − 7 9n + 2 − 9m + 2 < ε
46
eşitsizliğini sağlayacak şekilde var olduğudur. ε > 0 olsun. Bir N tamsayısı 27ε
değerinden daha büyük olacak şekilde seçilsin (bu seçimin nedeni aşağıda izah
edilmektedir). Herhangi n, m ≥ N pozitif tamsayıları göz önüne alınsın. Buna
göre
3n − 7 3m − 7 (27nm + 6n − 63m − 14) − (27mn + 6m − 63n − 14) 9n + 2 − 9m + 2 = (9n + 2)(9m + 2)
69 |m − n|
69 m + n
69m − 69n
<
≤
= 81mn + 18n + 18m + 4
81 mn
81 mn
23 1
46
1
1
23 1
<
=
+
+
<ε
=
27 n m
27 N
N
27N
sağlandığından verilen dizinin bir Cauchy dizisi olduğu sonucu elde edilir.
Örnek 2.4.3. {xn }n∈N = (−1)n n+1
dizisinin bir Cauchy dizisi olmadın
n∈N
ğını tanımı kullanarak gösteriniz.
Çözüm. Gösterilmesi gereken bir ε > 0 sayısına karşılık her N pozitif tamsayısının m, n ≥ N için
nn+1
m m + 1
|xn − xm | = (−1)
≥ε
− (−1)
n
m 54
eşitsizliğini sağladığıdır. ε = 2 olsun. Herhangi bir N pozitif tamsayısı göz
önüne alınsın ve n = 2N ve m = 2N + 1 olsun. Buna göre istenildiği üzere
n ≥ N ve m ≥ N sağlanır. Diğer taraftan
nn + 1
m m + 1
|xn − xm | = (−1)
− (−1)
n
m 2N 2N + 1
2N +1 (2N + 1) + 1 = (−1)
− (−1)
2N
2N + 1 2N + 1 (2N + 1) + 1 1 = 1 + 1 + 1 +
= +
2N
2N + 1 2N
2N + 1 1
1
=2+
+
>2=ε
2N
2N + 1
gerçeklendiğinden verilen dizinin bir Cauchy dizisi olmadığı sonucu elde edilir.
Aşağıdaki iki netice Cauchy dizisi olmanın süreklilik ile ne şekilde bağlantılı
olduğunu ortaya koymaktadır.
Açıklama 2.4.4. Eğer {xn } dizisi yakınsak ise bir Cauchy dizisidir.
Kanıt. {xn } dizisi yakınsak olduğundan n → ∞ iken xn → a sağlanır. Tanıma
göre, verilen bir ε > 0 sayısına karşılık n ≥ N için |xn − a| < ε/2 olacak şekilde
bir N ∈ N sayısı vardır. Dolayısıyla eğer n, m ≥ N ise üçgen eşitsizliğine göre
|xn −xm | = |xn −xm +a−a| = |(xn −a)−(xm −a)| ≤ |xn −a|+|xm −a| <
ε ε
+ =ε
2 2
sağlanır. Yani, {xn } bir Cauchy dizisidir.
Aşağıdaki teorem, Açıklama 2.4.4’nin tersinin de (reel değerli diziler için)
doğru olduğunu göstermektedir.
Teorem 2.4.5 (Cauchy). {xn } reel sayıların bir dizisi olsun. Buna göre {xn }
dizisinin Cauchy dizisi olabilmesi için gerek ve yeter şart {xn }’nin (bir a ∈ R
noktasına) yakınsamasıdır.
Strateji: Açıklama 2.4.4’den ötürü sadece her Cauchy dizisinin yakınsak olduğunu göstermek gerekir. {xn } bir Cauchy dizisi olsun. Buna göre xn terimleri birbirlerine yakın olduklarından {xn } dizisi sınırlı olmalıdır. Dolayısıyla,
Bolzano-Weierstrass Teoremi’ne göre {xn } dizisinin xnk gibi bir yakınsak alt
dizisi vardır. Yani, k’nın büyük değerleri için xnk ’lar bir a ∈ R noktasının yakınında yer alırlar. Fakat {xn } bir Cauchy dizisi olduğundan yeterince büyük n
değerleri için xn terimleri ile xnk ’lar yakındırlar. Dolayısıyla büyük n değerleri
için xn terimleri a noktasının yakınında yer alır. Buna göre tüm dizi aynı bir
a noktasına yakınsar.
55
Kanıt. {xn } bir Cauchy dizisi olsun ve ε = 1 verilsin. Cauchy dizisi olma
tanımına göre
n, m ≥ N için |xn − xm | < 1
olacak şekilde bir N ∈ N doğal sayısı vardır. Özel olarak bu ifade her m ≥ N
için |xN − xm | < 1 olacak şekilde bir N ∈ N sayısı vardır formunda yazılabilir.
Dolayısyla, üçgen eşitsizliği kullanılarak m ≥ N için
|xm | − |xN | ≤ |xm − xN | = |xN − xm | < 1 olduğundan |xm | < 1 + |xN |
elde edilir. Buna göre {xn } dizisi M = max{|x1 |, |x2 |, · · · , |xN −1 |, 1 + |xN |}
ile sınırlıdır (Her Cauchy dizisi sınırlıdır). Yani her n için |xn | ≤ M sağlanır.
Gerçekten, eğer n < N ise |xn | yukarıdaki maksimumu elde etmede kullanılan
terimlerden bir tanesidir. Diğer taraftan n ≥ N olması durumunda |xn | ≤
1 + |xN | eşitsizliği sağlandığından 1 + |xN | bir sınırdır.
Bolzano-Weierstrass Teoremi’ne göre {xn } dizisi n → ∞ iken xnk → a
olacak şekilde yakınsak bir alt diziye sahiptir. xn bir Cauchy dizisi olduğundan,
n, m ≥ N1 için |xn − xm | <
ε
2
eşitsizliğini sağlayacak şekilde bir N1 ∈ N sayısı seçilebilir. n → ∞ iken xnk → a
olduğundan
ε
k ≥ N2 için |xnk − a| <
2
ifadesini gerçekleyen bir N2 ∈ N vardır. nk ≥ N1 olacak şekilde k ≥ N2 sayısı
sabitlensin. Buna göre her n ≥ N1 için
|xn − a| ≤ |xn − xnk | + |xnk − a| < ε
elde edilir. Dolayısıyla, n → ∞ iken xn → a olduğu sonucuna ulaşılır.
Genellikle bir dizinin Cauchy dizisi olduğunu göstermek verilen dizinin yakınsak olduğunu göstermekten daha kolay olduğundan bu sonuç teoride önemli
bir yer teşkil eder. Aşağıdaki örnek bu durumun bir uygulamasıdır.
Örnek 2.4.6. n ∈ N için
1
2n
eşitsizliğini sağlayan her {xn } reel sayı dizisinin yakınsak olduğunu gösteriniz.
|xn − xn+1 | ≤
Çözüm. Eğer m > n ise
|xn − xm | = |xn − xn+1 + xn+1 − xn+2 + · · · + xm−1 − xm |
≤ |xn − xn+1 | + |xn+1 − xn+2 | + · · · + |xm−1 − xm |
1
1
1
≤ n + n+1 + · · · + m−1
2
2
2
56
1
1
elde edilir. Şimdi 21n + 2n+1
+ · · · + 2m−1
toplamının değerini hesaplayalım. Bu
1
toplam değerine T dersek ve T ’yi 2 ile çarpar kendisinden çıkartırsak
1
1
1
+ n+1 + · · · + m−1
n
2
2
2
1
1
1
1
− n+1 − · · · − m−1 − m
− T =
2
2
2
2
1
1
1
1
1
T = n − m ⇒T =2
− m
2
2
2
2n
2
T =
elde edilir. Burada 1/2m ifadesi pozitif olduğundan
1
1
1
1
1
1
1
≤ 2 n = n−1 ,
+
+
·
·
·
+
=
2
−
2n
2n+1
2m−1
2n
2m
2
2
yani tüm m > n ≥ 1 tamsayıları için
|xn − xm | ≤
1
2n−1
sağlanır. Diğer taraftan biliyoruz ki Archimedean Özelliği’ne göre verilen her
ε > 0 sayısına karşılık n ≥ N için 1/2n−1 < ε eşitsizliğini sağlayacak şekilde
bir N ∈ N doğal sayısı vardır. Buna göre {xn } bir Cauchy dizisidir. Teorem
2.4.5’e göre her Cauchy dizisi yakınsak olduğundan verilen dizinin yakınsadığı
bir reel sayının varlığı garantidir.
Aşağıdaki sonuç yeterince büyük n değerleri için xn ile xn+1 terimlerinin
yakın olmasının, verilen dizinin bir Cauchy dizisi olmasını gerektirmediğini vurgulamaktadır.
Açıklama 2.4.7. xn+1 − xn → 0 özelliğini sağlayan her dizinin bir Cauchy
dizisi olması şart değildir.
Kanıt. xn := log n olsun. Logaritmanın temel özelliklerinden biliyoruz ki
xn+1 − xn = log(n + 1) − log n = log
n + 1 n→∞
→ log 1 = 0
n
sağlanır. Diğer taraftan {xn } bir Cauchy dizisi olamaz. Çünkü n → ∞ iken
dizi +∞ değerine ıraksar.
Alıştırmalar
2.4.1. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu
tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) Eğer {xn } bir Cauchy dizisi ve {yn } sınırlı ise {xn yn } bir Cauchy dizisidir.
57
b) Eğer {xn } ve {yn } Cauchy dizileri ve her n ∈ N için yn 6= 0 ise {xn /yn } bir
Cauchy dizisidir.
c) Eğer {xn } ve {yn } Cauchy dizileri ve her n ∈ N için xn +yn > 0 ise {1/(xn /yn )}
sıfır değerine yakınsamaz.
d) Reel sayıların k → ∞ iken x2k − x2k−1 → 0 ve her k ∈ N için n 6= 2k koşullarını
sağlayan bir {xn } dizisi Cauchy dizisidir.
2.4.2. Her n ∈ N için
2n2 + 3
+ 5n2 + 3n + 1
eşitsizliğini sağlayan {xn } dizisinin bir Cauchy dizisi olduğunu gösteriniz.
|xn | ≤
n3
2.4.3. Her n ∈ N için xn ∈ Z olsun. Buna göre {xn } bir Cauchy dizisi ise xn ’nin
sonuçta bir sabit olduğunu, yani her n ≥ N için xn = a olacak şekilde bir a ∈ Z ve
n ∈ N sayılarının varlığını gösteriniz.
2.4.4. {xn } ve {yn } herhangi iki Cauchy dizisi ve a ∈ R olsun.
a) Teorem 2.4.5’ü kullanmadan axn dizisinin de bir Cauchy dizisi olduğunu gösteriniz.
b) Teorem 2.4.5’ü kullanmadan xn + yn dizisinin de bir Cauchy dizisi olduğunu
gösteriniz.
c) Teorem 2.4.5’ü kullanmadan xn yn dizisinin de bir Cauchy dizisi olduğunu gösteriniz.
2.4.5. {xn } bir reel sayı dizisi olsun. Farz edelim ki her ε > 0 sayısına karşılık
P
m ≥ n ≥ N için m
k=n zk < ε olacak şekilde bir N ∈ N sayısı var olsun. Buna göre
lim
n→∞
n
X
xk
k=1
limitinin var ve sonlu olduğunu gösteriniz.
2.4.6. Gösteriniz ki limn→∞
Pn
k=1 (−1)
k
/k limiti vardır ve sonludur.
2.4.7. {xn } bir dizisi olsun. Eğer her n ∈ N için
|xn+1 − xn | ≤ an
eşitsizliğini sağlayan bir a ∈ (0, 1) reel sayı var ise xn → x olacak şekilde bir x ∈ R
sayısının varlığını gösteriniz.
a) Reel sayıların bir E alt kümesi göz önüne alınsın. Her r > 0 için E ∩
(a − r, a + r) arakesiti sonsuz sayıda nokta içeriyor ise a ∈ R sayısına E’nin bir
kapanış noktası adı verilir. İspatlayınız ki, a sayısının E kümesinin bir kapanış
noktası olması için gerek ve yeter şart her r > 0 için E ∩ (a − r, a + r)\{a}
kümesinin boştan farklı olmasıdır.
b) R’nin her sınırlı sonsuz alt kümesinin en az bir kapanış noktası olduğunu ispatlayınız.
2.4.8.
58
PSfrag
a) R’nin bir E alt kümesinin dizisel kompakt olarak adlandırılması için
gerek ve yeter şart her xn ∈ E dizisinin, limit değeri E’nin elemanı olan bir
yakınsak alt diziye sahip olmasıdır. Her kapalı sınırlı aralığın dizisel kompakt
olduğunu ispatlayınız.
b) R içerisinde dizisel kompakt olmayan sınırlı aralıkların varlığını gösteriniz.
c) R içerisinde dizisel kompakt olmayan kapalı aralıkların varlığını gösteriniz.
2.4.9.
2.5
Limit Supremum ve Limit İnﬁmum
Formal tanımı vermeden önce açıklayıcı olması bakımından aşağıdaki irdelemeyi yapalım:
{xn } terimleri R kümesine ait bir dizi olsun. Buna göre her n ∈ N için
Xn = {xk : k ≥ n}
kümesinin R’de inﬁmumu vardır. Yani her k ≥ n için
inf Xn ≤ xk
sağlanır.
R
inf Xn
.
.
−∞
+∞
her k ≥ n için xk elemanları burada yer alır
Her n için Xn ⊇ Xn+1 olduğundan {tn } = {inf Xn } artan bir dizidir.
inf X1 inf X3
R
.
.
−∞
+∞
inf X2 inf X4
Benzer şekilde Xn kümesinin supremumu vardır. Buna göre her k ≥ n için
xk ≤ sup Xn
sağlanır.
59
sup Xn
R
.
.
−∞
+∞
her k ≥ n için xk elemanları burada yer alır
Ayrıca her n için Xn+1 ⊆ Xn+1 olduğundan {sn } = {sup Xn } azalan bir dizidir.
Sonuç olarak k ≥ n için
inf Xn ≤ xk ≤ sup Xn
eşitsizliği sağlanır.
sup X4 sup X2 R
.
.
−∞
+∞
sup X3 sup X1
inf Xn
sup Xn
.
−∞
R ∪ {−∞, ∞}
.
+∞
her k ≥ n için xk elemanları burada yer alır
n değerleri büyüdükçe [inf Xn , sup Xn ] kapalı aralığı küçülür. Dolayısıyla dizinin sonlu kısmı hariç bizim asıl ilgilendiğimiz bölümünün ne kadar küçük bir
aralığa sıkışacağını gözlemleyebiliriz.
inf Xn′
sup Xn′
inf Xn
sup Xn
.
R ∪ {−∞, ∞}
.
+∞
−∞
n′ > n
Tanım 2.5.1. {xn } bir reel sayı dizisi olsun. Buna göre {xn } dizisinin limit
supremumu
(2.4)
lim sup xn := lim sup xk
n→∞
n→∞
60
k≥n
ve {xn } dizisinin limit inﬁmumu
lim inf xn := lim
n→∞
n→∞
inf xk
k≥n
genişletilmiş reel sayılarıdır.
Tanım 2.5.1’de verilen limitlerin genişletilmiş reel sayı olarak varlığının gösterilmesi gerekir. Bunun için {xn } reel sayı dizisi ve
sn = sup xk := sup{xk : k ≥ n} ve tn = inf xk := inf{xk : k ≥ n}
k≥n
k≥n
dizileri göz önüne alınsın. Yukarıda anlatıldığı üzere sn ve tn ’lerin her biri
genişletilmiş reel sayılardır ve Monotonluk Özelliğine göre sn genişletilmiş reel
sayıların azalan ve tn ise artan bir dizisi olduğundan n → ∞ iken sn ↓ s ve
tn ↑ t olacak şekilde s ve t genişletilmiş reel sayıları vardır (bkz Alıştırma 2.3.7).
Bu genişletilmiş reel sayılar, sırası ile, Tanım 2.5.1’e göre {xn } dizisinin limit
supremum ve limit inﬁmum değerleridir.
Aşağıdaki üç örnekte limit supremum ve limit inﬁmumun ne şekilde hesaplandığı gösterilmektedir.
Örnek 2.5.2. xn = (−1)n olsun. lim supn→∞ xn ve lim inf n→∞ xn değerlerini
tespit ediniz.
Çözüm. Her n ∈ N için supk≥n (−1)k = 1 olduğundan Tanım 2.5.1’e göre
lim supn→∞ xn = 1’dir. Benzer şekilde lim inf n→∞ xn = −1 olarak bulunur. Örnek 2.5.3. xn = 1+1/n olsun. lim supn→∞ xn ve lim inf n→∞ xn değerlerini
tespit ediniz.
Çözüm. Her n ∈ N için supk≥n (1 + 1/k) = 1 + 1/n olduğundan Tanım 2.5.1’e
göre lim supn→∞ xn = 1’dir. Diğer taraftan, her n ∈ N için inf k≥n (1 + 1/k) = 1
olduğundan lim inf n→∞ xn = 1 şeklinde elde edilir.
Örnek 2.5.4. xn = (−1)n n olsun. lim supn→∞ xn ve lim inf n→∞ xn değerlerini
tespit ediniz.
Çözüm. Verilen dizi {−1, 2, −3, 4, −5, 6, −7, · · · } şeklinde yazılabilir. Buna göre
her n ∈ N için supk≥n (−1)n n = ∞ olduğundan lim supn→∞ xn = ∞’dir. Diğer
taraftan, her n ∈ N için inf k≥n (−1)n n = −∞ olduğundan lim inf n→∞ xn =
−∞ şeklinde elde edilir.
Teorem 2.5.5. {xn } bir reel sayı dizisi, s = lim supn→∞ xn ve t = lim inf n→∞ xn
olsun. Buna göre k → ∞ iken xnk → s ve j → ∞ iken xℓj → s olacak şekilde
{xnk }k∈N ve {xℓj }j∈N alt dizileri vardır.
61
Kanıt. İspatı sadece limit supremum için vereceğiz. Benzer argüman kullanılarak teoremin doğruluğu limit inﬁmum için de gösterilebilir. sn = supk≥n xk
olsun. Buna göre n → ∞ iken sn ↓ s gerçeklenir.
Durum 1. s = ∞ olsun. Tanıma göre her n ∈ N için sn = ∞’dir. s1 = ∞
olduğundan xn1 > 1 olacak şekilde bir n1 ∈ N sayısı vardır. sn1 +1 = ∞
olduğundan xn2 > 2 olacak şekilde bir n2 ≥ n1 + 1 > n1 sayısı mevcuttur. Bu
şekilde devam ederek, her k ∈ N için xnk > k olacak şekilde bir {xnk } alt dizisi
seçilebilir. Dolayısıyla, R için Sıkıştırma Teoremi’ne (bkz Alıştırma 2.2.8) göre
k → ∞ iken xnk → ∞ = s olur.
Durum 2. s = −∞ olsun. Her n ∈ N için sn ≥ xn ve n → ∞ iken sn → −∞
olduğundan R için Sıkıştırma Teoremi’ne göre n → ∞ iken xn → −∞ = s
sağlanır.
Durum 3. −∞ < s < ∞ olsun. n0 = 0 alınsın. Teorem 1.3.5’e (Supremum için
Yaklaşım Teoremi) göre sn0 +1 − 1 < xn1 ≤ sn0 +1 eşitsizliğini sağlayacak bir
n1 ∈ N tamsayısı vardır. Benzer şekilde, sn1 +1 − 1/2 < xn2 ≤ sn1 +1 eşitsizliğini
sağlayacak bir n2 ≥ n1 + 1 > n1 tamsayısı mevcuttur. Bu anlamda devam
ederek her k ∈ N için
snk−1 +1 −
1
< xnk ≤ snk−1 +1
k
(2.5)
eşitsizliğini sağlayacak şekilde n1 < n2 < · · · tamsayıları seçilebilir. k → ∞
iken snk−1 +1 → s olduğundan Sıkıştırma Teoremi’ne göre k → ∞ iken xnk → s
elde edilir.
Teorem 2.5.6. {xn } bir reel sayı dizisi ve x bir genişletilmiş reel sayı olsun.
Buna göre n → ∞ iken xn → x olması için gerek ve yeter şart
lim sup xn = lim inf xn
n→∞
n→∞
(2.6)
eşitliğinin sağlanmasıdır.
Kanıt. n → ∞ iken xn → x olsun. {xn } dizisinin her {xnk } alt dizisi için n →
∞ iken xnk → x yazılabilir. Buna göre, Teorem 2.5.5’den lim supn→∞ xn = x
ve lim inf n→∞ xn = x ifadeleri gerçeklenir. Dolayısıyla, (2.6) eşitliği doğrudur.
Tersine, (2.6) ifadesi doğru olsun.
Durum 1. x = ±∞ olsun. Eğer terimler ±xn şeklinde göz önüne alınırsa x =
∞ olduğunu söyleyebiliriz. Buna göre, verilen bir M ∈ R için inf k≥N xk >
M olacak şekilde bir N ∈ N vardır. Dolayısıyla, her n ≥ N için xn > M
gerçeklenir. Bu ise n → ∞ iken xn → x olduğu anlamına gelir.
62
Durum 2. −∞ < x < ∞ ve ε > 0 olsun. Ayrıca
sup xk − x <
k≥N
ε
ε
ve x − inf xk <
k≥N
2
2
olacak şekilde bir N ∈ N seçilsin.
n, m ≥ N olsun ve basitlik sağlaması bakımından xn > xm eşitsizliğinin
doğruluğu kabul edilsin. Buna göre
|xn − xm | = xn − xm ≤ sup xk − x + x − inf xk <
k≥N
k≥N
ε ε
+ =ε
2 2
elde edilir. Dolayısıyla, {xn } dizisi bir Cauchy dizisidir ve sonlu bir reel sayıya
yakınsar. Bununla beraber, Teorem 2.5.5’e göre {xn } dizisinin x’e yakınsayan
bir alt dizisi mevcuttur. Bu ise n → ∞ iken xn → x olduğu anlamına gelir.
Teorem 2.5.5 bize limit supremum ve limit inﬁmum hakkında aşağıdaki
geometrik yorumu yapma imkânı tanır.
Teorem 2.5.7. {xn } bir reel sayı dizisi olsun. Buna göre lim supn→∞ xn (sırası
ile, lim inf n→∞ xn ) değeri, {xn } dizisinin bazı alt dizilerinin yakınsadığı (veya
değerin ∞ olması durumunda ıraksadığı) en büyük (sırası ile, en küçük) genişletilmiş sayıdır. Yani, k → ∞ iken xnk → x ise
lim inf xn ≤ x ≤ lim sup xn
n→∞
(2.7)
n→∞
eşitsizliği gerçeklenir.
Kanıt. k → ∞ iken xnk → x olsun. Bir N ∈ N sayısı sabitlensin ve k ≥ K
iken nk ≥ N olacak şekilde yeterince büyük bir K sayısı seçilsin. Buna göre
her k ≥ K için
inf xj ≤ xnk ≤ sup xj
j≥N
j≥N
eşitsizliği doğrudur. k → ∞ iken yukarıdaki ifadenin limiti alınırsa
inf xj ≤ x ≤ sup xj
j≥N
j≥N
elde edilir. Son eşitsizlikten bu kez N → ∞ iken limit alır ve Tanım 2.5.1
kullanılırsa (2.7) ifadesi elde edilir.
Açıklama 2.5.8. Reel sayıların herhangi bir {xn } dizisi için
lim inf xn ≤ lim sup xn
n→∞
n→∞
eşitsizliği gerçeklenir.
63
Kanıt. Her n ∈ N için inf k≥n xk ≤ x ≤ supk≥n xk eşitsizliği gerçeklendiğinden
Teorem 2.2.9 (Karşılaştırma Teoremi) kullanılarak verilen ifadenin doğruluğu
görülür.
Aşağıdaki ifadenin doğruluğu Tanım 2.5.1, Karşılaştırma Teoremi ve Monoton Yakınsaklık Teoremi kullanılarak gösterilebilir.
Açıklama 2.5.9. Bir {xn } dizisinin alttan sınırlı olması için gerek ve yeter şart lim supn→∞ xn < ∞ ve üstten sınırlı olması için gerek ve yeter şart
lim inf n→∞ xn > −∞ ifadelerinin gerçeklenmesidir.
Aşağıdaki sonuç bize eşitsizliklerin limit supremum ve limit inﬁmumlarını
alabileceğimizi belirtir.
Teorem 2.5.10. Büyük n değerleri için xn ≤ yn eşitsizliği sağlanıyor ise
lim sup xn ≤ lim sup yn ve lim inf xn ≤ lim inf yn
n→∞
n→∞
n→∞
n→∞
(2.8)
ifadeleri doğrudur.
Kanıt. Her k ≥ N için xk ≤ yk ise her n ≥ N için supk≥n xk ≤ supk≥n yk
ve inf k≥n xk ≤ inf k≥n yk eşitsizlikleri gerçeklenir. Eğer bu ifadelerden n → ∞
iken limit alınırsa (2.8) elde edilir.
Alıştırmalar
2.5.1. Aşağıdaki dizilerin limit supremum ve limit inﬁmum değerlerini hesaplayınız.
a)
b)
c)
d)
e)
f)
g)
xn
xn
xn
xn
xn
xn
xn
= 3 − (−1)n
= cos(nπ/2)
=√
(−1)n+1 + (−1)n /n
= 1 + n2 /(2n − 5)
= yn /n, burada yn üstten sınırlı bir dizidir
= n(1 + (−1)n ) + n−1 ((−1)n − 1)
= (n3 + n2 − n + 1)/(n2 + 2n + 5)
2.5.2. {xn } bir reel sayı dizisi olsun. Buna göre
− lim sup xn = lim inf (−xn )
n→∞
n→∞
ve
− lim inf xn = lim inf (−xn )
n→∞
n→∞
olduğunu gösteriniz.
2.5.3. {xn } bir reel sayı dizisi ve r ∈ R olsun.
64
a) Büyük n değerleri için
lim sup xn < r iken xn < r
n→∞
olduğunu ispatlayınız.
b) Sonsuz çoklukta n ∈ N için
lim sup xn > r iken xn > r
n→∞
olduğunu ispatlayınız.
2.5.4. {xn } ve {yn } reel sayıların herhangi iki dizisi olsun.
a) Aşağıdaki toplamların hiç birinin ∞ − ∞ formunda olmaması koşulu altında
lim inf xn + lim inf yn ≤ lim inf (xn + yn )
n→∞
n→∞
n→∞
≤ lim sup xn + lim inf yn
n→∞
n→∞
≤ lim sup(xn + yn ) ≤ lim sup xn + lim sup yn
n→∞
n→∞
n→∞
olduğunu ispatlayınız.
b) Eğer limn→∞ xn limiti mevcut ise
lim inf (xn + yn ) = lim xn + lim inf yn
n→∞
n→∞
n→∞
ve
lim sup(xn + yn ) = lim xn + lim sup yn
n→∞
n→∞
n→∞
eşitliklerini ispatlayınız.
2.5.5. {xn } ve {yn } reel sayıların herhangi iki dizisi olsun.
a) Her n ∈ N için xn ≥ 0 ve yn ≥ 0 olsun. Aşağıdaki eşitsizliğin sağındaki çarpım
0 · ∞ formunda olmamak üzere
lim sup(xn yn ) ≤ (lim sup xn )(lim sup yn )
n→∞
n→∞
n→∞
olduğunu gösteriniz.
b) Her n ∈ N için xn ≤ 0 ≤ yn olsun. Aşağıdaki eşitsizlikte bulunan çarpımların
hiç biri 0 · ∞ formunda olmamak üzere
(lim inf xn )(lim sup yn ) ≤ lim inf (xn yn )
n→∞
n→∞
n→∞
olduğunu gösteriniz.
2.5.6. Her n ∈ N için xn ≥ 0 ve yn ≥ 0 olsun. n → ∞ iken xn → x (burada x bir
genelleştirilmiş reel sayı da olabilir) ise aşağıdaki eşitlikte bulunan çarpımların hiç
biri 0 · ∞ formunda olmamak üzere
lim sup(xn yn ) = x lim sup yn
n→∞
n→∞
olduğunu gösteriniz.
65
2.5.7. Herhangi bir reel {xn } dizisi için
lim sup xn = inf sup xk ve lim inf xn = sup inf xk
n→∞
n∈N
n→∞
k≥n
n∈N
k≥n
olduğunu gösteriniz.
2.5.8. Her n ∈ N için xn ≥ 0 olsun. 1/0 = ∞ ve 1/∞ = 0 yorumları altında
lim sup
n→∞
1
1
1
1
=
ve lim inf
=
n→∞ xn
xn
lim inf n→∞ xn
lim supn→∞ xn
olduğunu gösteriniz.
66
3 R Üzerinde Fonksiyonlar
3.1
İki-Yönlü Limitler
Bölüm 2’de reel sayıların limitlerini inceledik. Bu bölümde ise tanım ve değer
kümeleri R’nin bir alt kümesi olan reel fonksiyonların limitleri üzerinde duracağız. Bu formdaki fonksiyonları, değer kümesi aynı zamanda ∞ ve/veya −∞
değerlerini içeren fonksiyonlardan ayırmak için reel fonksiyonları kimi zaman
sonlu değerli olarak isimlendireceğiz.
Tanım 3.1.1. a ∈ R, I reel sayıların a noktasını içeren bir açık aralığı ve f
muhtemelen a noktasında olmasa da bu I aralığı üzerindeki diğer tüm noktalarda tanımlı bir reel fonksiyon olsun. Buna göre x noktası a noktasına yaklaşırken f (x) fonksiyonunun L’ye yakınsıyor olarak adlandırılması için gerek ve
yeter şart her ε > 0 sayısına karşılık
0 < |x − a| < δ olduğu müddetçe |f (x) − L| < ε
(3.1)
eşitsizliğini sağlayan bir δ > 0 (bu sayı genellikle ε, f , I ve a niceliklerine
bağlıdır) sayısının var olmasıdır.
Bu durumda
L = lim f (x) veya x → a iken f (x) → L
x→a
yazılır ve x noktası a noktasına yaklaşırken f (x) fonksiyonunun limiti L’dir
şeklinde okunur.
Tanım 3.1.1’e göre verilen bir fonksiyonun limiti olduğunu göstermek için
genel bir ε > 0 değeri ile başlayıp (3.1) ifadesini sağlayan δ sayısının nasıl
seçilmesi gerektiği ortaya konmalıdır.
Örnek 3.1.2. m, b ∈ R olmak üzere f (x) = mx + b olarak tanımlansın. Buna
göre her a ∈ R için
f (a) = lim f (x)
x→a
olduğunu ispatlayınız.
y
y = f (x)
L+ε
L
L−ε
a+δ a
a−δ
x
Kanıt. Eğer m = 0 ise ispat gerektiren bir durum yoktur. Diğer durumda, ε > 0
sayısı verilsin ve δ = ε/|m| olarak seçilsin. Eğer |x − a| < δ ise bu durumda
|f (x) − f (a)| = |mx + b − (ma + b)| = |m||x − a| < |m|δ = ε
ifadesi sağlanacağından δ sayısının bu seçimi ile x → a iken f (x) → f (a) olduğu
elde edilir.
Kimi durumlarda δ sayısını belirlemek için f (x) − L ifadesini iki çarpan
şeklinde yazmamız gerekebilir. Daha sonra önemsiz olduğu düşünülen çarpan
bir üst sınırı ile değiştirilerek istenilen elde edilir.
Örnek 3.1.3. f (x) = x2 + x − 3 olarak tanımlansın. Buna göre x → 1 iken
f (x) → −1 olduğunu ispatlayınız.
Kanıt. ε > 0 ve L = −1 olsun. Buna göre
f (x) − L = x2 + x − 3 − (−1) = x2 + x − 2 = (x − 1)(x − 2)
bulunur. Eğer 0 < δ ≤ 1 ise |x−1| < δ olduğundan |x−1| < 1 yani −1 < x−1 <
1 dolayısıyla 0 < x < 2 elde edilir. Buna göre üçgen eşitsizliği kullanılarak
|x + 2| ≤ |x| + 2 < 4 eşitsizliğine ulaşılır. δ = min{1, ε/4} olsun. δ sayısının bu
seçimi ile eğer |x − 1| < δ ise
|f (x) − L| = |x − 1||x − 2| < 4|x − 1| < 4δ ≤ ε
elde edilir. Bu ise tanıma göre x → 1 iken f (x) → −1 demektir.
Örnek 3.1.4. limx→a x2 = a2 olduğunu ispatlayınız.
Kanıt. Her x ∈ R için f (x) := x2 olsun. Gösterilmesi gereken
|f (x) − L| = |f (x) − a2 | = |x2 − a2 |
68
farkının, x değerleri a’ya yeterince yakın olmak üzere, önceden atanmış bir ε
değerinden küçük olduğudur. Buna göre x2 − a2 = (x − a)(x + a) olduğundan,
eğer |x−a| < 1 ise üçgen eşitsizliği kullanılarak |x|−|a| ≤ |x−a| < 1nyani |x| <
o
ε
1 + |a| dolayısıyla |x + a| ≤ |x| + |a| < 1 + 2|a| elde edilir. δ = min 1, 2|a|+1
olsun. δ sayısının bu seçimi ile |x − a| < δ ise
|f (x) − L| = |x − a||x + a| < |x − a|(1 + 2|a|) < (1 + 2|a|)δ ≤ ε
sonucuna ulaşılır. Bu ise tanıma göre x → a iken f (x) → a2 demektir.
Örnek 3.1.5. a > 0 için x → a iken
1
x
→
1
a
olduğunu ispatlayınız.
Kanıt. Her x > 0 için f (x) := 1/x ve a > 0 olsun. Gösterilmesi gereken
1 1 1
|f (x) − L| = f (x) − = − a
x a
farkının, x değerleri a > 0’ya yeterince yakın olmak üzere, önceden atanmış bir
ε değerinden küçük olduğudur. Buna göre x > 0 için
1
− 1 = 1 (a − x) = 1 |x − a|
ax
x a ax
olduğundan 1/(ax) ifadesi için bir üst sınır bulmak gerekir. Özel olarak eğer
|x − a| < 12 a ise − 12 a < x − a < 12 a olduğundan a − 21 a < x < a + 12 a yani
1
3
1
2
2 a < x < 2 a sonuçta x < a elde edilir. Dolayısıyla
|x − a| <
1
2
1
a için 0 <
< 2
2
ax
a
sonucuna ulaşılır. Buna göre x’in bu değerleri için
f (x) − 1 < 2 |x − a|
a a2
elde edilir. Yukarıdaki eşitsizliğin sağ tarafının ε’dan küçük kalmasını garantile
mek için |x − a| < 21 a2 ε alınmalıdır. Sonuç olarak δ = min 21 a, 12 a2 ε şeklinde
seçilirse eğer |x − a| < δ ise
|f (x) − L| =
2
2
|x − a| < 2 δ ≤ ε
2
a
a
sonucuna ulaşılır. Bu ise tanıma göre x → a iken f (x) → 1/a demektir.
Devam etmeden önce Tanım 3.1.1’in iki önemli özelliğine değinelim: Kabul
1. I bir açık aralıktır; Kabul 2. 0 < |x − a| sağlanır. Eğer I = (c, d) bir açık
aralık ve δ0 := min{a − c, d − a} olarak belirlenirse |x − a| < δ0 için x ∈ I
sağlanır. Dolayısıyla, Kabul 1 yeterince küçük δ > 0 için |x − a| < δ (a’nın
69
her iki tarafında) koşulunu sağlayan her x 6= a noktasında f (x) fonksiyonu
tanımlıdır. |x − a| > 0 olduğundan x 6= a’dır ve Kabul 2 f fonksiyonu bu
noktada tanımlı olmasa dahi f ’in limitinin a olabileceğini garantiler (Bu olgu
daha sonra türevleri tanımlarken kritik bir rol oynayacaktır).
Aşağıdaki sonuç f (x) fonksiyonu a noktasında tanımlı olsa dahi a noktasında f ’in limitinin değerinin f (a) değerinden genellikle bağımsız olduğunu
ortaya koymaktadır.
Açıklama 3.1.6. a ∈ R, I reel sayıların a noktasını içeren bir açık aralığı
ve f, g muhtemelen a noktasında olmasa da bu I aralığı üzerindeki diğer tüm
noktalarda tanımlı birer reel fonksiyon olsun. Eğer her x ∈ I\{a} için f (x) =
g(x) ve x → a iken f (x) → L ise bu durumda x → a iken g(x) fonksiyonunun
da bir limit değeri vardır ve
lim g(x) = lim f (x)
x→a
x→a
sağlanır.
Kanıt. ε > 0 olsun. (3.1) ve |x − a| < δ için x ∈ I koşullarını sağlayacak şekilde
yeterince bir küçük δ > 0 sayısı seçilsin. 0 < |x − a| < δ eşitsizliğinin sağlandığı
kabul edilsin. Teorem hipotezine göre f (x) = g(x) ve (3.1)’den |f (x) − L| < ε
olduğundan |g(x) − L| < ε sonucu elde edilir.
Örnek 3.1.7. x → 1 iken
g(x) =
x3 + x2 − x − 1
x2 − 1
fonksiyonunun bir limit değeri olduğunu ispatlayınız.
Kanıt. f (x) = x + 1 olsun. Örnek 3.1.2’ye göre x → 1 iken f (x) → 2 sağlanır.
x 6= ±1 için
g(x) =
(x + 1)(x2 − 1)
x3 + x2 − x − 1
=
= x + 1 = f (x)
x2 − 1
x2 − 1
olduğundan Açıklama 3.1.6’ya göre x → 1 iken g(x) fonksiyonunun limiti vardır
(ve bu limit değeri 2’dir).
Dizilerin limitleri ile fonksiyonların limitleri arasında yakın bir ilişki vardır.
Teorem 3.1.8 (Limitlerin Dizisel Karakterizasyonu). a ∈ R, I reel sayıların a
noktasını içeren bir açık aralığı ve f muhtemelen a noktasında olmasa da bu I
aralığı üzerindeki diğer tüm noktalarda tanımlı bir reel fonksiyon olsun. Buna
göre
L = lim f (x)
x→a
70
limitinin mevcut olması için gerek ve yeter şart n → ∞ iken a değerine yakınsayan her xn ∈ I\{a} dizisi için n → ∞ iken f (xn ) → L olmasıdır.
Kanıt. x noktası a’ya yaklaşırken f fonksiyonu L değerine yakınsasın. Buna
göre verilen ε > 0 için (3.1) ifadesini sağlayacak şekilde bir δ > 0 sayısı vardır.
Diğer taraftan eğer xn ∈ I\{a} dizisi n → ∞ iken a değerine yakınsıyor ise
n ≥ N için |xn − a| < δ eşitsizliğini sağlayan bir N ∈ N sayısı seçilebilir. xn 6= a
olduğundan (3.1)’e göre her n ≥ N için |f (xn ) − L| < ε sağlanır. Bu ise n → ∞
iken f (xn ) → L demektir.
Tersine, n → ∞ iken a değerine yakınsayan her xn ∈ I\{a} dizisi için
n → ∞ iken f (xn ) → L olsun. Bu durumda, eğer x noktası a’ya yaklaşırken
f fonksiyonu L değerine yakınsamıyor ise bir ε > 0 sayısı için (biz bu sayıya
ε0 diyelim) “0 < |x − a| < δ olduğu müddetçe x ∈ I\{a} için |f (x) − L| < ε”
eşitsizliğini sağlayan hiç bir δ > 0 sayısı yoktur. Dolayısıyla n ∈ N olmak üzere
her δ = 1/n için 0 < |xn − a| < 1/n ve |f (xn ) − L| ≥ ε koşullarını sağlayan bir
xn ∈ I noktası vardır. Bu ise birinci koşul ve Sakıştırma Teoremi (Teorem 2.2.1)
gereği xn 6= a ve xn → a demektir. Sonuç olarak hipotez koşuluna göre n → ∞
iken f (xn ) → L sağlanır. Özel olarak, büyük n değerleri için |f (xn ) − L| < ε
olması ikinci koşul ile çelişir.
Yukarıdaki teorem gereği bir fonksiyonun x → a iken limit değerinin olmadığını göstermek için f altındaki görüntülerinin farklı limit değerlerine sahip
olduğu a değerine yakınsayan iki dizinin varlığını göstermek gerekir.
Örnek 3.1.9.
f (x) =

sin
0
1
x
x 6= 0
x=0
şeklinde tanımlanan fonksiyonun x → 0 iken limitinin olmadığını gösteriniz.
Kanıt. n ∈ N için
an :=
2
2
ve bn :=
(4n + 1)π
(4n + 3)π
olarak tanımlansın. Açıktır ki her iki dizi de n → ∞ iken 0 değerine yakınsar.
Diğer taraftan her n ∈ N için f (an ) = 1 ve f (bn ) = −1 olduğundan n → ∞
iken f (an ) → 1 ve f (bn ) → −1 gerçeklenir. Bu ise Teorem 3.1.8’e göre x → 0
iken f (x) fonksiyonunun limitinin olmadığı anlamına gelir.
f, g : E → R olsun. Her x ∈ E için f ve g fonksiyonlarının noktasal toplamı,
f +g
(f + g)(x) := f (x) + g(x),
71
bir α ∈ R skaleri ile f fonksiyonunun skaler çarpımı, αf
(αf )(x) := αf (x),
f ve g fonksiyonlarının noktasal çarpımı, f g
(f g)(x) := f (x)g(x)
ve son olarak da f ve g’nin (g(x) 6= 0 olmak üzere) noktasal bölümü, f /g
f
f (x)
(x) =
g
g(x)
şeklinde tanımlanır.
Aşağıdaki sonuç Teorem 2.2.4’ün fonksiyon analoğudur.
Teorem 3.1.10. a ∈ R, I reel sayıların a noktasını içeren bir açık aralığı
ve f, g muhtemelen a noktasında olmasa da bu I aralığı üzerindeki diğer tüm
noktalarda tanımlı birer reel fonksiyon olsun. x değerleri a’ya yaklaşırken f (x)
ve g(x) yakınsak ise (f + g)(x), (f g)(x), (αf )(x) ve (g(x) fonksiyonunun limiti
sıfırdan farklı olmak üzere) (f /g)(x) fonksiyonları da yakınsaktırlar. Aslında,
lim (f + g)(x) = lim f (x) + lim g(x),
x→a
x→a
x→a
lim (αf )(x) = α lim f (x),
x→a
x→a
lim (f g)(x) = lim f (x) lim g(x)
x→a
x→a
x→a
ve (g(x) fonksiyonunun limiti sıfırdan farklı olmak üzere)
f
limx→a f (x)
(x) =
lim
x→a
g
limx→a g(x)
eşitlikleri gerçeklenir.
Kanıt. i)
L := lim f (x) ve M := lim g(x)
x→a
x→a
olsun. Eğer xn ∈ I\{a} dizisi a değerine yakınsıyor ise Teorem 3.1.8’e göre n →
∞ iken f (xn ) → L ve g(xn ) → M sağlanır. Bu ise Teorem 2.2.4 ii) şıkkına göre
n → ∞ iken f (xn ) + g(xn ) → L + M demektir. Bu ifade a değerine yakınsayan
her xn ∈ I\{a} dizisi için doğru olduğundan Teorem 3.1.8 kullanılarak
lim (f + g)(x) = L + M = lim f (x) + lim g(x)
x→a
x→a
x→a
sonucu elde edilir. Diğer sonuçlar, Teorem 2.2.4 ii)-iv) neticeleri benzer şekilde
kullanılarak ispatlanır.
72
Diziler için verilen Sıkıştırma ve Karşılaştırma Teoremleri ile Limitlerin Dizisel Karakterizasyonu beraber düşünüldüğünde aşağıdaki sonuçlar elde edilir.
Teorem 3.1.11 (Fonksiyonlar için Sıkıştırma Teoremi). a ∈ R, I reel sayıların
a noktasını içeren bir açık aralığı ve f, g, h muhtemelen a noktasında olmasa da
bu I aralığı üzerindeki diğer tüm noktalarda tanımlı birer reel fonksiyon olsun.
i) Her x ∈ I\{a} için g(x) ≤ h(x) ≤ f (x) sağlanıyor ve
lim f (x) = lim g(x) = L
x→a
x→a
ise bu durumda x → a iken h(x) fonksiyonunun limiti vardır ve
lim h(x) = L
x→a
gerçeklenir.
ii) Her x ∈ I\{a} için |g(x)| ≤ M ve x → a iken f (x) → 0 ise
lim f (x)g(x) = 0
x→a
sağlanır.
y
y = f (x)
y = h(x)
.
L
a
y = g(x)
x
Teorem 3.1.12 (Fonksiyonlar için Karşılaştırma Teoremi). a ∈ R, I reel sayıların a noktasını içeren bir açık aralığı ve f, g muhtemelen a noktasında olmasa
da bu I aralığı üzerindeki diğer tüm noktalarda tanımlı birer reel fonksiyon olsun. Eğer f ve g fonksiyonlarının x değerleri a’ya yaklaşırken limitleri varsa
ve her x ∈ I\{a} için f (x) ≤ g(x) sağlanıyor ise
lim f (x) ≤ lim g(x)
x→a
x→a
eşitsizliği gerçeklenir.
73
Yukarıdaki limit teoremleri (Teorem 3.1.10, 3.1.11 ve 3.1.12) sayesinde ε ve
δ’ya başvurmadan limitlerin var olduğu ispatlanabilir.
Örnek 3.1.13.
lim
x→1
x−1
=0
3x + 1
olduğunu ispatlayınız.
Kanıt. Örnek 3.1.2’ye göre x → 1 iken x − 1 → 0 ve 3x + 1 → 4 elde edilir.
Teorem 3.1.10 kullanılarak x → 1 iken (x − 1)/(3x + 1) → 0/4 = 0 sonucuna
ulaşılır.
Alıştırmalar
3.1.1. a ∈ R, f ve g muhtemelen x = a noktasında olmasa da reel sayıların a
noktasını içeren bir açık aralığı üzerindeki diğer tüm noktalarda tanımlı birer reel
fonksiyon olsun. Buna göre aşağıdaki ifadelerin hangilerinin doğru hangilerinin yanlış
olduğunu belirleyiniz. Doğru olanları ispatlayıp yanlış olanlara ise ters örnek veriniz.
a) Her n ∈ N için x → a iken (x − a)n sin(f (x)(x − a)−n ) fonksiyonunun limiti
vardır.
b) xn 6= a olmak üzere {xn } dizisi a değerine yakınsasın. Eğer n → ∞ iken
f (xn ) → L ise x → a iken f (x) → L sağlanır.
c) f ve g fonksiyonları (a − 1, a + 1) açık aralığı üzerinde sonlu değerli ve x → a
iken f (x) → 0 ise x → a iken f (x)g(x) → 0 sağlanır.
d) a noktasını içeren bir I aralığı içerisindeki her x değeri için f (x) ≤ g(x) ve
limx→a f (x) limiti yoksa limx→a g(x) limiti de yoktur.
3.1.2. Tanım 3.1.1’i kullanarak aşağıdaki limitlerin herbirinin varlığını ispatlayınız.
a) limx→2 x2 + 2x − 5 = 3
b) limx→1
x2 +x−2
x−1
=3
3
c) limx→2 x + 2x + 1 = 4
2
d) limx→0 x3 sin(ex ) = 0
3.1.3. Aşağıdaki limitlerin hangilerinin var hangilerinin var olmadığına karar veriniz.
Cevabınızın doğruluğunu ispatlayınız.
a) limx→0 tan x1
2 b) limx→0 x cos x x+1
3
c) limx→1
1
log x
3.1.4. Aşağıdaki limitlerin hangilerinin var hangilerinin var olmadığına karar veriniz.
Cevabınızın doğruluğunu ispatlayınız.
a) limx→1
b) limx→1
x2 +2x−3
x3 −x
xn −1
x−1
n∈N
74
√
3
c) limx→1
x4 −1
cos(1−x)
d) limx→0
2 sin2 x+2x−2x cos2 x
1−cos2 (2x)
e) limx→0 tan x sin
1
x2
3.1.5. Teorem 3.1.11’i ispat ediniz.
3.1.6. Teorem 3.1.12’yi ispat ediniz.
3.1.7. f reel değerli bir fonksiyon olsun.
a) Eğer
L = lim f (x)
x→a
limiti varsa x → a iken |f (x)| → |L| olduğunu ispatlayınız.
b) x → a iken |f (x)| → |L| olduğu halde f (x)’in limitinin olmadığı f fonksiyonlarının varlığını gösteriniz.
3.1.8. Her reel değerli f fonksiyonu için f ’in pozitif kısmı
f + (x) =
|f (x)| + f (x)
, x ∈ Dom(f )
2
f − (x) =
|f (x)| − f (x)
, x ∈ Dom(f )
2
ve f ’in negatif kısmı
olarak tanımlanır.
a) Her x ∈ Dom(f ) için f + (x) ≥ 0, f − (x) ≥ 0, f (x) = f + (x) − f − (x) ve |f (x)| =
f + (x) + f − (x) olduğunu kanıtlayınız (Alıştırma 1.2.4 ile kıyaslayınız).
b) Eğer
L = lim f (x)
x→a
+
limiti varsa x → a iken f (x) → L
+
ve f − (x) → L− olduğunu ispatlayınız.
3.1.9. f ve g reel değerli fonksiyonlar ve her x ∈ Dom(f ) ∩ Dom(g) için
(f ∨ g)(x) := max{f (x), g(x)} ve (f ∧ g)(x) := min{f (x), g(x)}
olarak tanımlansın.
a) Her x ∈ Dom(f ) ∩ Dom(g) için
(f ∨ g)(x) =
(f + g)(x) + |(f − g)(x)|
2
(f ∧ g)(x) =
(f + g)(x) − |(f − g)(x)|
2
ve
olduğunu ispatlayınız.
b) Eğer
L = lim f (x) ve M = lim g(x)
x→a
x→a
limitleri varsa x → a iken (f ∨ g)(x) → L ∨ M ve (f ∧ g)(x) → L ∧ M sağlanır.
75
3.1.10. a ∈ R ve a noktasını içeren bir açık aralık I olsun. Eğer f : I → R fonksiyonu
x → a iken f (x) → f (a) oluyor ve m < f (a) < M eşitsizliğini sağlayan m ve M
sayıları varsa |x − a| < δ koşulunu sağlayan x değerleri için
m + ε < f (x) < M − ε
ifadesini gerçekleyen ε ve δ sayıları vardır.
3.2
Tek-Yönlü Limitler ve Sonsuzda Limit Kavramı
Bir önceki kısımda reel değerli bir fonksiyonun limitini tanımladık. Şimdi bu
tanımı daha gelen durumlarda
kullanılmak üzere genişletelim.
√
x → 1 iken f (x) := x − 1 fonksiyonunun limiti nedir? Makul bir cevap
limitin sıfır olduğu yönündedir. Fakat, bu fonksiyon a = 1 noktasını içeren bir
AÇIK aralıkta tanımlı olmadığından Tanım 3.1.1’in koşullarını gerçeklemez.
Aslında f fonksiyonu sadece x ≥ 1 için tanımlıdır. Bu tip problemlerle başa
çıkmak için “tek-yönlü limitler” kavramı kullanılmaktadır.
Tanım 3.2.1. a ∈ R ve f reel değerli bir fonksiyon olsun.
i) x noktası a noktasına sağdan yaklaşırken f (x) fonksiyonunun L’ye yakınsıyor olarak adlandırılması için gerek ve yeter şart, f fonksiyonu sol
uç-noktası a olan bir I açık aralığında tanımlı ve her ε > 0 sayısına
karşılık
a + δ ∈ I ve a < x < a + δ olduğu müddetçe |f (x) − L| < ε
(3.2)
eşitsizliğini sağlayan bir δ > 0 (bu sayı genellikle ε, f , I ve a niceliklerine
bağlıdır) sayısının var olmasıdır. Bu durumda
f (a+) := L =: lim f (x)
x→a+
yazılır ve fonksiyonunun a noktasındaki sağdan-limiti L’dir şeklinde okunur.
ii) x noktası a noktasına soldan yaklaşırken f (x) fonksiyonunun L’ye yakınsıyor olarak adlandırılması için gerek ve yeter şart, f fonksiyonu sağ
uç-noktası a olan bir I açık aralığında tanımlı ve her ε > 0 sayısına karşılık a − δ ∈ I ve a − δ < x < a olduğu müddetçe |f (x) − L| < ε eşitsizliğini
sağlayan bir δ > 0 (bu sayı genellikle ε, f , I ve a niceliklerine bağlıdır)
sayısının var olmasıdır. Bu durumda
f (a−) := L =: lim f (x)
x→a−
yazılır ve fonksiyonunun a noktasındaki soldan-limiti L’dir şeklinde okunur.
76
İki-yönlü limitler için bir önceki kısımda verilen tüm limit teoremlerinin tekyönlü limit söz konusu olduğunda da doğruluğu kolayca gösterilir. Bu anlamda
gerektiğinde söz konusu teoremleri tek-yönlü limitler için kullanma hakkına
sahibiz.
Tek-yönlü limitlerin varlığı limit teoremlerinden veya doğrudan tanımı kullanılarak gösterilebilir.
Örnek 3.2.2.
i) a = 0 noktasında

x + 1 x ≥ 0
f (x) =
x − 1 x < 0
şeklinde tanımlanan fonksiyonun tek-yönlü limitleri olduğunu fakat limx→0 f (x)
limitinin mevcut olmadığını gösteriniz.
ii) Aşağıdaki limitin varlığını ispatlayınız:
lim
x→0+
√
x = 0.
Kanıt. i) ε > 0 ve δ = ε olsun. Eğer 0 < x < δ ise |x − 0| = |x| < δ olduğundan |f (x) − 1| = |x + 1 − 1| = |x| < δ = ε gerçeklenir. Buna göre
limx→0+ f (x) limit değeri vardır ve 1’e eşittir. Benzer şekilde −δ < x < 0 ise
|f (x) − (−1)| = |x − 1 + 1| = |x| < δ = ε sağlandığından limx→0− f (x) limiti
var ve −1’e eşittir. Bununla beraber n → ∞ iken xn = (−1)n /n → 0 sağlanır,
fakat f (xn ) = (−1)n (1 + 1/n) yakınsak değildir. Dolayısıyla, Limitlerin Dizisel
Karakteristiği’nden ötürü limx→0 f (x) limiti mevcut değildir.
√
√
ii) ε > 0 ve δ = ε2 olsun. Eğer 0 < x < δ ise |f (x) − L| = | x| = x <
√
√
δ = ε elde edilir. Bu ise limx→0+ x = 0 demektir.
Her fonksiyonun tek-yönlü limitleri var olmak zorunda değildir (bkz Alıştırma 3.1.9). Alıştırma 3.2.2’de bir fonksiyonun tek yönlü limitleri olsa da iki-yönlü
limitinin olmayabileceği gösterilmektedir. Bununla beraber, aşağıdaki sonuç bir
a noktasında tek-yönlü limitler var ve birbirine EŞİT ise a noktasında fonksiyonun iki-yönlü limitinin var olduğunu ortaya koymaktadır.
Teorem 3.2.3. f bir reel değerli fonksiyon olsun. Buna göre
lim f (x)
x→a
limitinin var ve L değerine eşit olması için gerek ve yeter şart
L = lim f (x) = lim f (x)
x→a+
x→a−
ifadesinin sağlanmasıdır.
77
(3.3)
Kanıt. x → a iken f (x) fonksiyonunun limiti var ve L olsun. Verilen bir ε > 0
sayısı için 0 < |x − a| < δ olduğu müddetçe |f (x) − L| < ε eşitsizliğini sağlayan
bir δ > 0 sayısı seçilsin. Ayrıca a < x < a + δ ve a − δ < x < a eşitsizliklerini
sağlayan her x değeri için a − δ < x < a + δ yani −δ < x − a < δ olduğundan
0 < |x − a| < δ gerçeklenir. Buna göre f (x) fonksiyonunun x → a iken sağdan
ve soldan limitlerinin her ikiside vardır ve (3.3) ifadesi doğrudur.
Tersine (3.3) ifadesi doğru olsun ve bir ε > 0 sayısı verilsin. Buna göre
a < x < a + δ1 (sırası ile, a − δ2 < x < a) olduğu müddetçe |f (x) − L| < ε
eşitsizliğini sağlayan bir δ1 (sırası ile, δ2 ) sayısı vardır. δ = min{δ1 , δ2 } olsun.
0 < |x − a| < δ ise ya a < x < a + δ1 ya da 1 − δ2 < x < a (x noktasının a’nın
sağında ya da solunda yer almasına bağlı) sağlanır. Dolayısıyla (3.1) ifadesi
gerçeklenir. Yani, x → a iken f (x) → L’dir.
Reel değerli fonksiyonların limitleri kavramı genişletilmiş reel sayılara aşağıdaki şekilde uygulanabilir.
Tanım 3.2.4. a, L ∈ R ve f reel değerli bir fonksiyon olsun.
i) x → ∞ iken f (x) fonksiyonu L değerine yakınsıyor olarak adlandırılması
için gerek ve yeter şart (c, ∞) ⊂ Dom(f ) içermesini sağlayan bir c > 0
sayısının ve verilen ε > 0 sayısına karşılık x > M olduğu müddetçe
|f (x) − L| < ε eşitsizliğini gerçekleyecek şekilde bir M ∈ R sayısının var
olmasıdır. Bu durumda
lim f (x) = L veya x → ∞ iken f (x) → L
x→∞
yazılır. Benzer şekilde x → −∞ iken f (x) fonksiyonu L değerine yakınsıyor olarak adlandırılması için gerek ve yeter şart (−∞, −c) ⊂ Dom(f )
içermesini sağlayan bir c > 0 sayısının ve verilen ε > 0 sayısına karşılık
x < M olduğu müddetçe |f (x) − L| < ε eşitsizliğini gerçekleyecek şekilde
bir M ∈ R sayısının var olmasıdır. Bu durumda
lim f (x) = L veya x → −∞ iken f (x) → L
x→−∞
yazılır.
ii) x → a iken f (x) fonksiyonu ∞ değerine yakınsıyor olarak adlandırılması
için gerek ve yeter şart I\{a} ⊂ Dom(f ) içermesini sağlayan a noktasını
da içeren bir I açık aralığının ve verilen M ∈ R sayısına karşılık 0 <
|x − a| < δ olduğu müddetçe f (x) > M eşitsizliğini gerçekleyecek şekilde
bir δ > 0 sayısının var olmasıdır. Bu durumda
lim f (x) = ∞ veya x → a iken f (x) → ∞
x→a
78
yazılır. Benzer şekilde, x → a iken f (x) fonksiyonu −∞ değerine yakınsıyor olarak adlandırılması için gerek ve yeter şart I\{a} ⊂ Dom(f )
içermesini sağlayan a noktasını da içeren bir I açık aralığının ve verilen
M ∈ R sayısına karşılık 0 < |x − a| < δ olduğu müddetçe f (x) < M
eşitsizliğini gerçekleyecek şekilde bir δ > 0 sayısının var olmasıdır. Bu
durumda
lim f (x) = −∞ veya x → a iken f (x) → −∞
x→a
yazılır.
Tanım 3.2.4 kullanılarak x → a+ ve x → a− iken f (x) → ±∞ ve x → ±∞
iken f (x) → ±∞ limitleri de tanımlanabilir ki bu durumlar öğrenciye ödev
olarak bırakılmıştır.
Örnek 3.2.5.
i) x → ∞ iken 1/x → 0 olduğunu ispatlayınız.
x+2
= −∞ olduğunu ispatlayınız.
ii) limx→1− f (x) := limx→1− 2
2x − 3x + 1
Kanıt. i) ε > 0 verilsin ve M = 1/ε olsun. Eğer x > M ise |1/x| = 1/x <
1/M = ε sağlanır. Buna göre x → ∞ iken 1/x → 0 gerçeklenir.
ii) M ∈ R olsun. Göstermemiz gereken 1’in civarında fakat solunda yer alan
x değerleri için f (x) < M (M sayısının ne kadar büyük ve negatif olduğunun önemi olmaksızın) eşitsizliğinin sağlandığıdır. Genelliği bozmadan M < 0
olduğu kabul edilsin. x, 1’e soldan yaklaşırken 2x2 − 3x + 1 negatif değerler
alır ve 0’a yakınsar (dikkat edilirse aslında 2x2 − 3x + 1 kolları yukarı doğru
uzanmış x eksenin 1/2 ve 1 noktalarında kesen bir paraboldür). Buna göre
1 − δ < x < 1 aralığındaki x değerleri için 2/M < 2x2 − 3x + 1 < 0 olacak şekilde bir δ ∈ (0, 1) sayısı seçilebilir. Dolayısıyla −1/(2x2 − 3x + 1) > −M/2 > 0
gerçeklenir. Diğer taraftan 0 < x < 1 olduğundan 2 < x + 2 < 3 sağlanır. Bu
ise −(x + 2)/(2x2 − 3x + 1) > −M yani her 1 − δ < x < 1 için
f (x) =
2x2
x+2
<M
− 3x + 1
sonucu elde edilir.
Tek-yönlü, çift-yönlü ve sonsuz limitleri tek türlü belirli bir şekilde göstermek için aşağıdaki notasyonu tanımlayalım. a bir genişletilmiş reel sayı, I ya a
noktasını içeren ya da bir uç noktası a olan dejenere olmayan bir açık aralık ve
f muhtemelen a noktasında olmasa da I açık aralığı üzerinde tanımlanmış reel
değerli bir fonksiyon olsun. Eğer a sonlu ve I aralığı a noktasını içeriyor ise
lim f (x)
x→a
x∈I
79
(3.4)
noktasyonu limx→a f (x) (limitin olması durumunda); eğer a değeri sonlu ve
I aralığının sol uç noktası ise (3.4) notasyonu limx→a− f (x) (limitin olması
durumunda); eğer a değeri sonlu ve I aralığının sağ uç noktası ise (3.4) notasyonu limx→a+ f (x) (limitin olması durumunda); eğer a = ±∞ ve I aralığının
bir uç noktası ise (3.4) notasyonu limx→±∞ f (x) (limitin olması durumunda)
limitlerini temsil edecektir.
Yukarıdaki şekilde tanımlanan notasyon kullanılarak Limitlerin Dizisel Karakterizasyonu çift-yönlü, tek-yönlü ve sonsuz limitler için aşağıdaki şekilde
verilir.
Teorem 3.2.6. a bir genişletilmiş reel sayı ve I ya a noktasını içeren ya da bir
uç noktası a olan dejenere olmayan bir açık aralık ve f muhtemelen a noktasında olmasa da I açık aralığı üzerinde tanımlanmış reel değerli bir fonksiyon
olsun. Buna göre
lim f (x)
x→a
x∈I
limitinin var ve L değerine eşit olması için gerek ve yeter şart xn 6= a ve n → ∞
iken xn → a olan her xn ∈ I dizisi için f (xn ) → L limitinin gerçeklenmesidir.
Kanıt. Bu teoremin doğruluğu hali hazırda iki-yönlü limitler için gösterildiğinden (3.4) ifadesinin temsil ettiği diğer limit durumları için ispatı yapmak
yeter. Tüm durumlara ait kanıtlar benzer tarzda hareket ederek ortaya koyulabileceğinden biz sadece a noktasının I aralığına ait ve L = ∞ olması halini
inceleyeceğiz. Gösterilmesi gereken x → a iken f (x) → ∞ limitinin gerçeklenmesi için gerek ve yeter şartın her n ∈ N için xn 6= a ve a değerine yakınsayan
tüm xn ∈ I dizileri için f (xn ) → ∞ olduğudur.
x → a iken f (x) → ∞ olsun. Eğer xn ∈ I, n → ∞ iken xn → a ve xn 6= a ise
verilen bir M ∈ R sayısına karşılık 0 < |x − a| < δ olduğu müddetçe f (x) > M
eşitsizliğini sağlayacak şekilde bir δ > 0 sayısı ve n ≥ N için |xn − a| < δ
eşitsizliğini sağlayacak şekilde bir n ∈ N sayısı vardır. Sonuç olarak, n ≥ N
eşitsizliğini sağlayan xn terimleri için f (xn ) > M gerçeklenir. Bu ise istenildiği
gibi n → ∞ iken f (xn ) → ∞ olduğu anlamına gelir.
Tersine, xn 6= a olan ve a değerine yakınsayan tüm xn ∈ I dizileri için
f (xn ) → ∞ limiti sağlansın, fakat x → a iken f (x) fonksiyonu ∞ değerine
yakınsamasın. ∞’a “yakınsamanın” tanımına göre her n ∈ N için f (xn ) ≤ M0
ve |xn − a| < 1/n eşitsizliklerini gerçekleyen M0 ∈ R ve xn ∈ I sayıları vardır.
Dolayısıyla, n → ∞ iken xn → a sağlanır fakat f (xn ) fonksiyonu ∞ değerine
yakınsamaz. Bu ise a ∈ I ve L = ∞ durumunda Teorem 3.2.6’te elde edilen
sonuç ile çelişir.
80
Teorem 3.2.6 kullanılarak Teorem 2.2.7 ve Sonuç 2.2.8 ile verilen limit teoremlerinin fonksiyonlar için analogları ispatlanabilir. Bu limit teoremleri kullanılarak sonsuz limitler ve ±∞’da limitler hesaplanır.
Örnek 3.2.7. limx→∞
2x2 − 1
= −2 olduğunu ispatlayınız.
1 − x2
Kanıt. Çarpımın limiti limitlerin çarpımı olduğundan her m ∈ N için Örnek
3.2.5 i)’ye göre x → ∞ iken 1/xm → 0 sağlanır. Yukarıda verilen ifadenin payı
ve paydası 1/x2 ile çarpılırsa
2 − 1/x2
limx→∞ (2 − 1/x2 )
2
2x2 − 1
=
lim
=
=
= −2
x→∞ −1 + 1/x2
x→∞ 1 − x2
limx→∞ (−1 + 1/x2 )
−1
lim
elde edilir.
Alıştırmalar
3.2.1. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu
tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) Eğer x → ∞ iken f (x) → ∞ ve g(x) > 0 ise x → ∞ iken g(x)/f (x) → 0
sağlanır.
b) Eğer x → a+ iken f (x) → 0 ve her x ∈ R için g(x) ≥ 1 ise x → a+ iken
g(x)/f (x) → ∞ sağlanır.
c) Eğer x → ∞ iken f (x) → ∞ ise x → ∞ iken sin(x2 + x + 1)/f (x) → 0 sağlanır.
d) Eğer P derecesi Q’nün derecesine eşit ya da küçük iki polinom ise (bkz Alıştırma
3.2.4)
P (x)
P (x)
= lim
=L
lim
x→−∞ Q(x)
x→∞ Q(x)
olacak şekilde bir L ∈ R sayısı vardır.
3.2.2. Aşağıda verilen ifadelerin her biri için tanımları kullanarak (limit teoremleri
yerine) limitlerin varlığını ispatlayınız. Limit değerlerini belirleyiniz.
√
a) limx→0− x2 /x
b) limx→∞ sin x/x2
c) limx→−1+ 1/(x2 − 1)
d) limx→1+ (x − 3)/(3 − x − 2x2 )
e) limx→−∞ (cos(tan x))/(x + 1)
3.2.3. Her a ∈ R için x → a iken ex → ea , sin x → sin a ve cos x → cos a olduğunu
kullanarak aşağıdaki limitleri eğer varsa hesaplayınız.
a)
b)
c)
d)
e)
f)
limx→2− (x3 − x2 − 4)/(x2 − 4)
limx→∞ (5x2 + 3x − 2)/(3x2 − 2x + 1)
2
limx→−∞ e−1/x
2
limx→0+ ex +2x−1 / sin x
√
limx→0− √
sin(x + π/2)/ 3 cos x − 1
limx→0+ 1 − cos x/ sin x
81
3.2.4. Her j = 0, 1, 2, · · · , n için aj ∈ R ve an 6= 0 olmak üzere
P (x) = an xn + an−1 xn−1 + · · · + a1 x + a0
formundaki bir fonksiyona n. dereceden polinom adı verilir.
a) Eğer 00 = 1 ise her n = 0, 1, · · · ve a ∈ R için limx→a xn = an olduğunu
ispatlayınız.
b) Eğer P bir polinom ise her a ∈ R için
lim P (x) = P (a)
x→a
olduğunu ispatlayınız.
3.2.5. a ∈ R olmak üzere f ve g reel değerli fonksiyonlar için aşağıdaki karşılaştırma
teoremlerini ispatlayınız.
a) Eğer x → a iken g(x) → ∞ ve f (x) ≥ g(x) ise x → a iken f (x) → ∞ sağlanır.
b) Eğer f (x) ≤ g(x) ≤ h(x) ve
L := lim f (x) = lim h(x)
x→∞
x→∞
ise x → ∞ iken g(x) → L sağlanır.
3.2.6. Teorem 3.2.6’ün şu özel durumunu ispatlayınız: a ∈ R için f : [a, ∞) → R
olsun. x → ∞ iken f (x) → L limitinin gerçeklenmesi için gerek ve yeter şart n → ∞
iken ∞ değerine yakınsayan her xn ∈ (a, ∞) dizisi için f (xn ) → L olmasıdır.
3.2.7. f : [0, 1] → R ve her a ∈ [0, 1] için f (a) = limx→a f (x) olsun. Buna göre
her q ∈ Q ∩ [0, 1] için f (q) = 0 eşitliğinin sağlanması için gerek ve yeter şartın her
x ∈ [0, 1] için f (x) = 0 ifadesinin gerçeklenmesi olduğunu ispatlayınız.
3.2.8. P bir polinom ve bir a ∈ R sabiti için P (a) > 0 olsun. Buna göre x → a+
iken P (x)/(x − a) → ∞ ve x → a− iken P (x)/(x − a) → −∞ olduğunu fakat
lim
x→a
P (x)
x−a
limitinin var olmadığını ispatlayınız.
3.2.9. [Cauchy] f : N → R olsun. Eğer
lim f (n + 1) − f (n) = L
n→∞
ise limn→∞ f (n)/n limitinin var ve L değerine eşit olduğunu ispatlayınız.
82
3.3
Süreklilik
Biliyoruz ki bir fonksiyonun a noktasında sürekli olması için a ∈ Domf ve
x → a iken f (x) → f (a) sağlanmalıdır. Aslında burada üstü kapalı bir şekilde
de olsa f ’in a noktasının her iki tarafında√tanımlı olduğu kabul edilmektedir.
Şimdi daha genel halde x = 0 noktasında x gibi, verilen bir noktanın sadece
bir yönünde tanımlı olan bir fonksiyonun sürekliliğinin de içerildiği aşağıdaki
tanımı verelim.
Tanım 3.3.1. R’nin boştan farklı bir alt kümesi E ve f : E → R olsun.
i) f fonksiyonunun bir a ∈ E noktasında sürekli olarak adlandırılması için
gerek ve yeter şart verilen ε > 0 sayısına karşılık
|x − a| < δ ve x ∈ E olduğu müddetçe |f (x) − f (a)| < ε
(3.5)
eşitsizliğini sağlayacak şekilde bir δ > 0 (genellikle bu sayı ε, f ve a
niceliklerine bağlıdır) sayısının var olmasıdır.
ii) f fonksiyonunun E üzerinde sürekli (notasyon: f : E → R sürekli) olarak
adlandırılması için gerek ve yeter şart f ’in her x ∈ E noktasında sürekli
olmasıdır.
Aşağıdaki sonuç eğer E kümesi a noktasını içeren bir açık aralık ise “f fonksiyonu a noktasında süreklidir” ifadesinin “x → a iken f (x) → f (a)” yazmaya
denk olduğunu göstermektedir. Dolayısıyla, E’nin bir açık aralık olması durumunda “f fonksiyonu a ∈ E noktasında süreklidir” yerine kısaca “f fonksiyonu
a noktasında süreklidir” şeklinde belirtiriz.
Açıklama 3.3.2. a noktasını içeren bir açık aralık I ve f : I → R olsun. f
fonksiyonunun a ∈ I noktasında sürekli olması için gerek ve yeter şart
f (a) = lim f (x)
x→a
ifadesinin sağlanmasıdır.
Kanıt. I = (c, d) ve δ0 := min{|c − a|, |d − a|} olsun. Eğer δ < δ0 ise |x − a| < δ
eşitsizliğini sağlayan x değerleri için x ∈ I sağlanır. Dolayısıyla f (a) = L,
E = I ve δ < δ0 için (3.5) ifadesi (3.1)’e denk olur. Buna göre f fonksiyonunun
a noktasında sürekli olması için gerek ve yeter şart x → a iken f (x) → f (a)
sağlanmasıdır.
Teorem 3.1.8’in ispatındaki şekilde hareket ederek herhangi boştan farklı
bir kümenin üzerinde sürekliliğin dizisel karakterizasyonunu aşağıdaki şekilde
verebiliriz.
83
Teorem 3.3.3. R’nin boştan farklı bir alt kümesi E, a ∈ E ve f : E → R
olsun. Buna göre aşağıdaki ifadeler birbirine denktir.
i) a ∈ E noktasında f süreklidir.
ii) Eğer xn dizisi a değerine yakınsıyor ve xn ∈ E ise n → ∞ iken f (xn ) →
f (a)’dır.
√
Özel olarak x fonksiyonu Alıştırma 2.2.6’ya göre I = [0, ∞) aralığında
süreklidir.
Teorem 3.3.3 ve Teorem 2.2.4 birlikte düşünüldüğünde aşağıdaki sonuç elde
edilir.
Teorem 3.3.4. R’nin boştan farklı bir alt kümesi E ve f, g : E → R olsun.
Eğer f , g fonksiyonları bir a ∈ E noktasında (sırası ile, E kümesi üzerinde)
sürekli ise f + g, f g ve αf (α ∈ R) fonksiyonları da a noktasında (sırası ile,
E üzerinde) süreklidir. Ayrıca, g(a) 6= 0 (sırası ile, her x ∈ E için g(x) 6= 0)
olmak üzere f /g fonksiyonu da a noktasında (sırası ile, E üzerinde) süreklidir.
Alıştırma 3.1.7, 3.1.8 ve 3.1.9 göz önüne alındığında eğer f ve g fonksiyonları
sırası ile, bir a ∈ E noktasında ya da E kümesi üzerinde sürekli ise |f |, f + , f − ,
f ∨ g ve f ∧ g fonksiyonları da söz konusu a ∈ E noktasında ya da E kümesi
üzerinde süreklidir. Ayrıca Alıştırma 3.2.4’e göre her polinom R’de süreklidir.
Pek çok komplike fonksiyon toplamlar, çarpımlar, bölümler ve aşağıda tanımlanan operasyon ile basit kısımlara ayrılabilir.
Tanım 3.3.5. R’nin iki alt kümesi A ve B, f : A → R ve g : B → R olsun.
Buna göre eğer f (A) ⊆ B ise g ile f ’in bileşkesi g ◦ f : A → R fonksiyonu x ∈ A
olmak üzere
(g ◦ f )(x) := g(f (x))
şeklinde tanımlanır.
Teorem 3.3.6. R’nin iki alt kümesi A ve B, f : A → R, g : B → R ve her
x ∈ A için f (x) ∈ B olsun.
i) I ya a noktasını içeren ya da bir uç noktası a olan dejenere olmayan bir
açık aralık, A := I\{a} olsun. Eğer
L := x→a
lim f (x)
x∈I
limiti var ve B kümesine ait ve g fonksiyonu L ∈ B noktasında sürekli
ise
!
lim (g ◦ f )(x) = g
x→a
x∈I
sağlanır.
84
lim f (x)
x→a
x∈I
ii) Eğer f fonksiyonu a ∈ A noktasında ve g fonksiyonu f (a) ∈ B noktasında
sürekli ise g ◦ f bileşke fonksiyonu da a ∈ A noktasında süreklidir.
Kanıt. i) xn ∈ I\{a} ve n → ∞ iken xn → a olsun. Açıkça f (A) ⊆ B olduğundan f (xn ) ∈ B gerçeklenir. Ayrıca, Limitlerin Dizisel Karakterizasyonu (Teorem 3.2.6) ötürü n → ∞ iken f (xn ) → L’dir. g fonksiyonu L ∈ B noktasında
sürekli olduğundan Teorem 3.3.3’e göre n → ∞ iken f (xn ) := g(f (xn )) → L
sağlanır. Bu ise Teorem 3.2.6’ya göre I aralığında x → a iken g ◦ f (x) → L
demektir. Yani i) ifadesi gerçeklenir. Benzer tarzda hareket ederek ii) şıkkının
doğruluğu gösterilebilir.
Pek çok uygulamada verilen bir fonksiyonun maksimum ve minimum değerlerini belirlemek önemli bir yer tutar. Bu amaçla ilk adım olarak aşağıdaki
konsepti ortaya koyalım.
Tanım 3.3.7. R’nin boştan farklı bir alt kümesi E olsun. Bir f : E → R
fonksiyonunun E üzerinde sınırlı olarak adlandırılması için gerek ve yeter şart
her x ∈ E için |f (x)| ≤ M eşitsizliğini sağlayacak şekilde bir M ∈ R sayısının
var olmasıdır. Bu durumda f fonksiyonu E üzerinde M ile domine edilmiştir
denir.
Dikkat edilirse bir f fonksiyonun E kümesi üzerinde sınırlı olup olmaması
E ve f ifadelerine bağlıdır. Örneğin, [1, ∞) aralığından f (x) = 1/x fonksiyonu
1 ile domine edilmiştir. Fakat aynı fonksiyon (0, 2) aralığında sınırsızdır. Diğer
taraftan, (−2, 2) aralığında f (x) = x2 fonksiyonu 4 ile domine edilmiş olmakla
birlikte [0, ∞) üzerinde sınırsızdır.
Sıkça kullanılacak aşağıdaki sonçta kapalı ve sınırlı bir aralıkta sürekli olan
fonksiyonların her zaman sınırlı olduğu gösterilmektedir.
Teorem 3.3.8 (Ekstremum Değer Teoremi). Eğer I aralığı kapalı, sınırlı ve f :
I → R fonksiyonu I üzerinde sürekli ise bu durumda f fonksiyonu I üzerinde
sınırlıdır. Ayrıca,
M = sup f (x) ve m = inf f (x)
(3.6)
x∈I
x∈I
ise
f (xM ) = M ve f (xm ) = m
olacak şekilde xm , xM ∈ I noktaları vardır.
Kanıt. Farzedelim ki f fonksiyonu I üzerinde sınırlı olmasın. Buna göre
|f (xn )| > n, n ∈ N
(3.7)
eşitsizliğini sağlayan xn ∈ I vardır. I aralığı sınırlı olduğundan Bolzano-Weierstrass Teoremi’ne (Teorem 2.3.9) göre {xn } dizisinin yakınsak bir alt dizisi
85
vardır. Bu yakınsak alt dizi xnk olsun. Buna göre k → ∞ iken xnk → a gerçeklenir. Ayrıca, yine I sınırlı olduğundan Karşılaştırma Teoremi (Teorem 2.2.9)
gereği a ∈ I’dır ve özel olarak f (a) ∈ R sağlanır. Diğer taraftan, (3.7) ifadesinde
n yerine nk yazar ve bu eşitsizlikten k → ∞ iken limit alınırsa |f (a)| = ∞ elde
edilir ki bu ise f (a) ∈ R olması ile çelişir. Şu durumda f fonksiyonu I üzerinde
sınırlı olmalıdır.
Yukarıda gösterildi ki M ve m sonlu reel sayılardır. Şimdi f (xM ) = M
eşitliğini sağalayan bir xM ∈ I sayısının var olduğunu göstermek için ifadenin
tersinin, yani her x ∈ I için f (x) < M sağlandığını farz edelim. Buna göre
g(x) =
1
M − f (x)
şeklinde tanımlanan fonksiyon I’da sürekli ve dolayısıyla I üzerinde sınırlıdır.
Özel olarak, |g(x)| = g(x) ≤ C eşitsizliğini sağlayacak şekilde C > 0 sayısı
mevcuttur. Dolayısıyla her x ∈ I için
1
(3.8)
C
ifadesi gerçeklenir. Tüm x ∈ I üzerinden (3.8) eşitsizliğinin supremumu alınır
ise
1
M ≤M−
C
elde edilir ki bu ise çelişkidir. Şu durumda f (xM ) = M olacak şekilde bir
xM ∈ I vardır. Benzer argüman kullanılarak f (xm ) = m eşitliğini sağlayan bir
xm ∈ I olduğu gösterilebilir.
f (x) ≤ M −
Teorem 3.3.8’de verilen M değerine I üzerinde f fonksiyonunun maksimumu, m değerine ise minimumu adı verilir.
Açıklama 3.3.9. Ekstremum Değer Teoremi’nin hipotezinden “kapalı” veya
“sınırlı” olma koşulları çıkarıldığında teorem doğru olmaz.
Kanıt. İsteneni göstermek için bir ters örnek vermek yeter. Sınırlı fakat kapalı
olmayan (0, 1) aralığı üzerinde f (x) = 1/x fonksiyonu süreklidir fakat sınırlı
değildir. Diğer taraftan sınırlı olmayan kapalı [0, ∞) aralığı üzerinde f (x) = x
fonksiyonu süreklidir fakat sınırlı değildir.
Bir aralıkta sürekli olan fonksiyonların graﬁklerinde delikler veya sıçramalar yoktur (bkz Teorem 3.3.11). Bu olgu kullanılarak aşağıdaki basit gözlem
verilebilir.
Lemma 3.3.10. a 0 ise buna göre x1 > x0 ve her x ∈ [x0 , x1 ] için f (x) > ε
eşitsizliğini sağlayacak şekilde bir ε pozitif sayısı ve x1 ∈ [a, b) noktası vardır.
86
Strateji: İspatın dayanak ﬁkri gayet basittir. Eğer f (x0 ) > 0 ise bu durumda
x0 ’ın civarındaki x değerleri için f (x) > f (x0 )/2 gerçeklenir. Şimdi detayları
verelim.
Kanıt. ε = f (x0 )/2 olsun. x0 < b olduğundan δ0 := (b − x0 )/2 sayısı pozitiftir
ve a ≤ x < x0 + δ0 eşitsizliğini sağlayan x değerleri için x ∈ [a, b) gerçeklenir.
Tanım 3.3.1 kullanılarak x ∈ [a, b) ve |x − x0 | < δ olduğu müddetçe |f (x) −
f (x0 )| < ε eşitsizliğini gerçekleyecek şekilde 0 < δ < δ0 sayısını seçelim.
Bir x1 ∈ (x0 , x0 + δ) sabitlensin ve x ∈ [x0 , x1 ] olsun. ε ve δ sayılarının
seçimlerinden ötürü açıkça
−
f (x0 )
f (x0 )
< f (x) − f (x0 ) <
2
2
gerçeklenir. Yukarıdaki eşitsizliğin sol tarafı f (x)’e göre çözülür ise f (x) >
f (x0 )/2 = ε elde edilir.
Bir y0 reel sayısının c ve d sayıları arasında yer alması için gerek ve yeter
şart c < y0 < d ya da d < y0 < c eşitsizliğinin gerçeklenmesidir.
Teorem 3.3.11 (Ara Değer Teoremi). a < b ve f : [a, b] → R sürekli bir
fonksiyon olsun. Eğer y0 sayısı f (a) ile f (b) arasında yer alıyor ise bu durumda
f (x0 ) = y0 olacak şekilde bir x0 ∈ (a, b) sayısı vardır.
Kanıt. f (a) < y0 < f (b) olsun. Aşağıdaki şekilde gösterildiği gibi bir E = {x ∈
[a, b] : f (x) < y0 } kümesi göz önüne alınsın. a ∈ E ve E ⊆ [a, b] olduğundan
E kümesi boştan farklıdır ve R’nin sınırlı bir alt kümesidir. Dolayısıyla Tamlık
Aksiyomu gereği x0 := sup E değeri sonlu bir reel sayı olarak mevcuttur. Buna
göre x0 ∈ (a, b) ve f (x0 ) = y0 olduğunu göstermek yeter.
y
f (b)
.
y0
f (a)
.
.
a
x0
87
b
x
Teorem 2.2.3 göz önüne alınarak n → ∞ iken xn → x0 olan bir xn ∈ E dizisi
seçilsin. E ⊆ [a, b] olduğundan Teorem 2.2.9 (Karşılaştırma Teoremi) gereği
x0 ∈ [a, b] gerçeklenir. Dolayısıyla f fonksiyonunun sürekliliği ve E kümesinin
tanımı göz önüne alındığında f (x0 ) = limn→∞ f (xn ) ≤ y0 elde edilir.
f (x0 ) = y0 olduğunu göstermek için ifadenin doğru olmadığını yani f (x0 ) <
y0 eşitsizliğinin sağlandığını farz edelim. Buna göre y0 − f (x) ifadesi [a, b) aralığında süreklidir ve x = x0 noktasında pozitif değer alır. Dolayısıyla, Lemma
3.3.10’a göre y0 − f (x1 ) > ε > 0 olacak şekilde x1 > x0 ve ε sayıları seçilebilir.
Buradan x1 ∈ E ve x1 > sup E çelişkisi elde edilir.
x0 ∈ [a, b] ve y0 = f (x0 ) olduğunu ispatladık. Kanıtın başında yaptığımız
f (a) < y0 < f (b) varsayımından ötürü x0 sayısı a veya b’ye eşit olamaz. Buna
göre x0 ∈ (a, b) sonucu elde edilir.
Yukarıdaki teorem gereği, eğer f fonksiyonu bir [a, b] aralığında sürekli ve
f (a) ≤ y0 ≤ f (b) ise f (x0 ) = y0 olacak şekilde bir x0 ∈ [a, b] sayısı vardır.
Eğer f fonksiyonu bir a noktasında sürekli değil ise f fonksiyonu a’da süreksiz dir denir ve a noktasına f ’in bir süreksizlik noktası adı verilir. Bir fonksiyonun bir süreksizlik noktası etrafındaki davranışı aşağıdaki örnekte incelenmektedir.
Örnek 3.3.12.
f (x) =

 |x|
x
1
x 6= 0
x=0
şeklinde tanımlanan fonksiyonun (−∞, 0) ve [0, ∞) aralıklarında sürekli ve 0
noktasında süreksiz olduğunu gösterip f (0+) ve f (0−) limit değerlerinin var
olduğunu ispatlayınız.
Kanıt. x ≥ 0 için |x| = x dolayısıyla f (x) = 1 olduğundan açıkça f (0+) = 1
limit değeri vardır ve her a > 0 için x → a iken f (x) → f (a) sağlanır. Buna
göre, f fonksiyonu [0, ∞) aralığında süreklidir. Benzer şekilde f (0−) = −1
limit değeri vardır ve f fonksiyonu (−∞, 0) aralığında süreklidir. Diğer taraftan,
f (0+) 6= f (0−) olduğundan Teorem 3.2.3’e göre x → 0 iken f (x) fonksiyonunun
limiti yoktur. Dolayısıyla f fonksiyonu 0 noktasında süreksizdir.
Örnek 3.3.13. sin x fonksiyonunun R’de sürekli olduğu kabulü altında

sin 1 x 6= 0
x
f (x) =
1
x=0
şeklinde tanımlanan fonksiyonun (−∞, 0) ve (0, ∞) aralıklarında sürekli ve 0
noktasında süreksiz olduğunu gösterip ne f (0+) ne de f (0−) limitlerinin var
olmadığını ispatlayınız.
88
Kanıt. Teorem 3.1.10’a göre 1/x fonksiyonu x 6= 0 için süreklidir. Dolayısıyla Teorem 3.3.6 kullanılarak f fonksiyonunun (−∞, 0) ve (0, ∞) üzerinde
sürekli olduğu sonucu elde edilir. f (0+) limitinin var olmadığını göstermek için
xn = 2/((2n + 1)π) olarak tanımlansın. Buna göre n ∈ N için sin(1/xn ) =
(−1)n ’dir. xn ↓ 0 olmakla birlikte (−1)n dizisi yakınsak değildir. Dolayısıyla
Teorem 3.3.3’e (Sürekliliğin Dizisel Karakterizasyonu) göre f (0+) limiti mevcut
değildir. Benzer argüman kullanılarak f (0−) değerinin var olmadığı gösterilebilir.
Örnek 3.3.14. R üzerinde

1 x ∈ Q
f (x) :=
0 x ∈
/Q
şeklinde tanımlanan fonksiyona Dirichlet fonksiyonu adı verilir. Dirichlet fonksiyonunun her x ∈ R noktasında süreksiz olduğunu gösteriniz (Bu tip fonksiyonlara hiçbir yerde sürekli fonksiyon adı verilir).
Kanıt. a bir rasyonel sayı ve {xn } irrasyonel sayıların a noktasına yakınsayan
bir dizisi olsun (Bu dizinin varlığı Teorem 1.3.9 ve Alıştırma 1.3.4 (Rasyonel ve
İrrasyonel Sayıların Yoğunluğu) göz önüne alındığında garantidir). Her n ∈ N
için f (xn ) = 0 olduğundan f (a) = 1 olmasına karşın f (xn ) → 0 gerçeklenir.
Buna göre f fonksiyonu herhangi bir rasyonel a noktasında sürekli olamaz.
Diğer taraftan b bir irrasyonel sayı ve {yn } rasyonel sayıların bu b değerine
yakınsayan bir dizisi olsun (Bu dizinin varlığı Teorem 1.3.9 (Rasyonel Sayıların Yoğunluğu) göz önüne alındığında garantidir). Her n ∈ N için f (yn ) = 1
olduğundan f (yn ) → 1 sağlanır. Fakat f (b) = 0 olduğundan f fonksiyonunun
herhangi bir irrasyonel b noktasında sürekli olmadığı sonucu elde edilir.
Her reel sayı ya rasyonel ya da irrasyonel olduğundan f fonksiyonunun R’de
hiç bir yerde sürekli olmadığı neticesine ulaşılır.
Örnek 3.3.15.
f (x) =

1
q
0
x=
p
q
x∈
/Q
∈ Q (indirgenmiş formda)
şeklinde tanımlanan fonksiyonun (0, 1) aralığındaki tüm irrasyonellerde sürekli
fakat (0, 1) aralığındaki tüm rasyoneller üzerinde süreksiz olduğunu kanıtlayınız.
89
Kanıt. a noktası (0, 1) aralığından bir rasyonel sayı ve farz edelim ki f fonksiyonu bu a noktasında sürekli olsun. Eğer xn irrasyonellerin a noktasına yakınsayan bir dizisi ise süreklilikten f (xn ) → f (a) yani f (a) = 0 gerçeklenir. Fakat
tanıma göre f (a) 6= 0 olduğundan çelişki elde edilir. Buna göre f fonksiyonu
(0, 1) aralığındaki tüm rasyoneller için süreksizdir.
(0, 1) aralığına ait bir irrasyonel sayı a olsun. Gösterilmesi gereken n → ∞
iken xn → a koşulunu sağlayan tüm xn ∈ (0, 1) dizilerinin aynı zamanda
f (xn ) → f (a) limitini de gerçeklediğidir. xn ∈ Q olsun. Her n ∈ N için dizinin terimleri indirgenmiş formda xn = pn /qn şeklinde yazılsın. f (a) = 0
olduğundan n → ∞ iken qn → ∞ limitini göstermek yeter. Tersine, her k ∈ N
için |qnk | ≤ M < ∞ eşitsizliğini sağlayacak şekilde n1 < n2 < · · · tamsayıları
var olsun. xnk ∈ (0, 1) olduğundan
E :=
pn
xnk = k : k ∈ N
qnk
şeklinde tanımlanan küme sadece sonlu sayıda eleman içerir. Buna göre E kümesinden alınan her dizinin limiti yine E kümesine ait olmalıdır. a bu limit
değerlerinden birisidir fakat a irrasyonel olduğundan kümeye ait olamaz. Dolayısıyla n → ∞ iken qn → ∞ ve buna göre f fonksiyonunun (0, 1) aralığındaki
tüm irrasyonellerde sürekli olduğu sonucu elde edilir.
Açıklama 3.3.16. f fonksiyonu sadece Q üzerinde ve g fonksiyonu da sadece
bir noktada süreksiz iki fonksiyon ise bu fonksiyonların g ◦ f bileşkeleri hiçbir
yerde sürekli olabilir.
Kanıt. f fonksiyonu Örnek 3.3.15’te göz önüne alınan fonksiyon ve

1 x 6= 0
g(x) =
0 x = 0
olsun. Buna göre

1 x ∈ Q
(g ◦ f )(x) =
0 x ∈
/Q
sağlanır. g ◦ f bileşke fonksiyonu Örnek 3.3.14 ile verilen hiçbir yerde sürekli
Dirichlet fonksiyonudur.
Aşağıdaki örneklerde gerektiğinde sin x, cos x ve ex fonksiyonlarının R’de
sürekli olduğu kabul edilecektir.
90
Alıştırmalar
3.3.1. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu
tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) Eğer f fonksiyonu [a, b] üzerinde sürekli ve J := f ([a, b]) ise J sınırlı ve kapalı
bir aralıktır.
b) Eğer [a, b] üzerinde f ve g sürekli, f (a) < g(a) ve f (b) > g(b) ise f (c) = g(c)
eşitsizliğini sağlayan bir c ∈ [a, b] sayısı vardır.
c) a noktasında f fonksiyonu sürekli ve f (a) 6= 0 olmak üzere a noktasını içeren bir
I aralığı üzerinde tanımlı sonlu değerli f ve g fonksiyonları göz önüne alınsın.
Buna göre g fonksiyonunun a noktasında sürekli olması için gerek ve yeter şart
f g fonksiyonunun a’da sürekli olmasıdır.
d) f ve g fonksiyonları R üzerinde tanımlı ve sonlu değerli olsun. Eğer f ve g ◦ f
fonksiyonları R üzerinde sürekli ise g’nin de R üzerinde süreklidir.
3.3.2. Limit teoremlerini kullanarak aşağıdaki fonksiyonların [0, 1] üzerinde sürekli
olduğunu gösteriniz.
a) f (x) =
ex
2√
sin x
cos x

 x2 +x−2
x 6= 1
x−1
3
x=1

e−1/x x 6= 0
c) f (x) =
0
x=0

√x sin 1 x =
6 0
x
d) f (x) =
0
x=0
b) f (x) =
3.3.3. Aşağıda verilen denklemleri gerçekleyen en az bir x ∈ R sayısının var olduğunu
gösteriniz.
a) ex = x3
b) ex = 2 cos x + 1
c) 2x = 2 − 3x
3.3.4. Eğer f : [a, b] → R fonksiyonu sürekli ise supx∈[a,b] |f (x)| değerinin sonlu
olduğunu ispatlayınız.
3.3.5. Eğer f : [a, b] → [a, b] fonksiyonu sürekli ise f ’in bir sabit noktasının, yani
f (c) = c eşitliğini sağlayan bir c ∈ [a, b] sayısının varlığını gösteriniz.
3.3.6. Eğer reel değerli f fonksiyonu bir a ∈ R noktasında sürekli bazı M ∈ R
noktalarında f (a) < M ise her x ∈ I için f (x) < M eşitsizliğini gerçekleyecek şekilde
a’yı içeren bir I açık aralığı vardır.
3.3.7. f + g toplam fonksiyonu R üzerinde sürekli olan f ve g hiçbir yerde sürekli
fonksiyonlarının varlığını gösteriniz. Bu fonksiyonların çarpımı için de benzer durumun söz konusu olduğunu gösteriniz.
91
3.3.8. a ∈ R, bu a noktasını içeren bir açık aralık I, f, g : I → R ve f fonksiyonu
a’da sürekli olsun. İspatlayınız ki g fonksiyonunun a noktasında sürekli olması için
gerek ve yeter şart f + g toplam fonksiyonunun a’da sürekli olmasıdır.
3.3.9. f : R → R fonksiyonu her x, y ∈ R için f (x + y) = f (x) + f (y) eşitliğini
gerçeklesin.
a) Her x ∈ R ve n ∈ Z için f (nx) = nf (x) olduğunu gösteriniz.
b) Her x ∈ R ve q ∈ Q için f (qx) = qf (x) olduğunu gösteriniz.
c) İspatlayınız ki f fonksiyonunun 0 noktasında sürekli olması için gerek ve yeter
şart f ’in R üzerinde sürekli olmasıdır.
d) İspatlayınız ki f fonksiyonu 0 noktasında sürekli ise her x ∈ R için f (x) = mx
eşitliğini sağlayacak şekilde bir m ∈ R sayısı vardır.
3.3.10. f : R → (0, ∞) fonksiyonu f (x + y) = f (x)f (y) eşitliğini gerçeklesin. İspatlayınız ki f fonksiyonu 0 noktasında sürekli ise her x ∈ R için f (x) = ax eşitliğini
sağlayacak şekilde bir a ∈ (0, ∞) sayısı vardır (Burada ax fonksiyonunun R üzerinde
olduğunu kabul ediyoruz).
3.3.11. f : R → R fonksiyonu R üzerinde sürekli ve
lim f (x) = lim f (x) = ∞
x→∞
x→−∞
ise f ’in R üzerinde bir minimumunun, yani
f (xm ) = inf f (x) < ∞
x∈R
ifadesini sağlayan bir xm ∈ R sayısının var olduğunu gösteriniz.
3.4
Düzgün Süreklilik
Tanım 3.4.1. R’nin boştan farklı bir alt kümesi E ve f : E → R bir fonksiyon
olsun. Buna göre f fonksiyonunun E üzerinde düzgün sürekli (notasyon: f :
E → R düzgün sürekli) olarak isimlendirilmesi için gerek ve yeter şart her
ε > 0 sayısına karşılık
|x − a| < δ ve x, a ∈ E olduğu müddetçe |f (x) − f (a)| < ε
(3.9)
eşitsizliğini sağlayacak şekilde δ > 0 sayısının var olmasıdır.
Dikkat edilirse Tanım 3.4.1’de söz konusu δ sayısı ε ve f niceliklerine bağlı
fakat a ve x değerlerine bağlı değildir. Bu durum bir küme üzerinde verilen bir
fonksiyonun düzgün sürekliliğini göstermek istendiğinde özellikle vurgulanması
gereken temel noktadır.
Örnek 3.4.2. (0, 1) aralığında f (x) = x2 fonksiyonunun düzgün sürekli olduğunu ispatlayınız.
92
Kanıt. ε > 0 verilsin ve δ = ε/2 olsun. Eğer x, a ∈ (0, 1) ise |x+a| ≤ |x|+|a| ≤ 2
sağlanır. Dolayısıyla x, a ∈ (0, 1) ve |x − a| < δ ise
|f (x) − f (a)| = |x2 − a2 | = |x − a||x + a| ≤ 2|x − a| < 2δ = ε
elde edilir.
Görüldüğü üzere süreklilik ve düzgün süreklilik tanımları birbirine benzer.
Tek fark, sürekli fonksiyonlarda δ parametresi a sayısına bağlı olabilirken düzgün sürekli fonksiyonlarda δ parametresi kesinlikle a’dan bağımsız seçilmelidir.
Tanımdan hemen anlaşılan bir sonuç E kümesi üzerinde düzgün sürekli tüm
fonksiyonların aynı zamanda E üzerinde sürekli olduğudur. Aşağıdaki örnek bu
durumun tersinin, bazı kısıtlamalar yapılmaksızın, her zaman doğru olmadığını
ortaya koymaktadır.
Örnek 3.4.3. Gösteriniz ki f (x) = x2 fonksiyonu R üzerinde düzgün sürekli
değildir.
Kanıt. f fonksiyonu R üzerinde düzgün sürekli olsun. Buna göre her x, a ∈ R
için |x−a| < δ olduğu müddetçe |f (x)−f (a)| < 1 eşitsizliğini sağlayan bir δ > 0
sayısı vardır. Archimedean Özelliği’ne göre nδ > 1 olacak şekilde yeterince
büyük bir n ∈ N sayısı seçilebilir. a = n ve x = n + δ/2 olsun. Dolayısıyla
|x − a| < δ ve
1 > |f (x) − f (a)| = |x2 − a2 | =
n+
δ
2
2
= n2 + nδ +
− n2
δ2
δ2
− n2 = nδ +
> nδ > 1
4
4
çelişkisi elde edilir. Bu çelişki f fonksiyonunun R üzerinde düzgün sürekli olmadığını ortaya koymaktadır.
Aşağıdaki sonuç süreklilik ve düzgün süreklilik arasında kilit rol oynamaktadır.
Lemma 3.4.4. E ⊆ R ve f : E → R düzgün sürekli olsun. Eğer xn ∈ E bir
Cauchy dizisi ise f (xn )’de bir Cauchy dizisidir.
Kanıt. ε > 0 olsun ve (3.9) ifadesini gerçekleyen bir δ > 0 sayısı seçilsin.
{xn } bir Cauchy dizisi olduğundan n, m ≥ N için |xn − xm | < δ eşitsizliğini
sağlayan bir N ∈ N sayısı vardır. Buna göre n, m ≥ N için aynı zamanda
|f (xn ) − f (xm )| < ε ifadesi gerçeklenir.
93
Dikkat edilirse (0, 1) aralığında f (x) = 1/x fonksiyonu sürekli ve xn =
1/n bir Cauchy dizisi olmasına karşın f (xn ) = n bir Cauchy dizisi değildir.
Aslında, (0, 1) aralığında 1/x sürekli fakat düzgün sürekli değildir. Bu durumu
y = 1/x fonksiyonunun graﬁği doğrular. Aşağıdaki şekilde görüldüğü üzere a
değeri 0’a yaklaştıkça δ değerleri küçülür (δ0 ve δ1 değerlerini mukayese ediniz).
Dolayısıyla δ sayısı a’dan bağımsız seçilemez.
y
f (x0 ) + ε
.
.
f (x0 ) − ε
.
f (x1 ) + ε
.
.
.
δ0
x0
}
}
f (x1 ) − ε
δ1
x1
x
Bir açık aralık üzerinde süreklilik ve düzgün süreklilik, her ne kadar aralık sınırlı olsa da, farklıdır. Aşağıdaki sonuç sınırlı kapalı aralıklar üzerinde
durumun bu şekilde olmadığını göstermektedir.
Teorem 3.4.5. I kapalı ve sınırlı bir aralık olsun. Bu durumda eğer f : I → R
fonksiyonu I üzerinde sürekli ise I üzerinde düzgün süreklidir.
Kanıt. Tersine, I üzerinde f fonksiyonu sürekli olsun fakat düzgün sürekli olmasın. Buna göre bir ε0 > 0 sayısı ve xn , yn ∈ I noktaları |xn − yn | < 1/n
ve
|f (xn ) − f (yn )| ≥ ε0 , n ∈ N
(3.10)
eşitsizliğini sağlayacak şekilde mevcuttur. Bolzano-Weierstrass Teoremi ve Karşılaştırma Teoremi’ne göre xn dizisinin xnk şeklinde k → ∞ iken bir x ∈ I
değerine yakınsayan bir alt dizisi mevcuttur. Benzer şekilde {ynk }k∈N dizisinin
ynkj şeklinde j → ∞ iken bir y ∈ I değerine yakınsayan bir alt dizisi mevcuttur.
j → ∞ iken xnkj → x ve f sürekli olduğundan (3.10) ifadesine göre |f (x) −
f (y)| ≥ ε0 , yani f (x) 6= f (y) sağlanır. Diğer taraftan her n ∈ N için |xn − yn | <
1/n olduğundan Teorem 2.2.1’e (Sıkıştırma Teoremi) göre x = y’dir. Bu ise
f (x) = f (y) çelişkisini doğurur.
Sınırlı açık aralıklar üzerinde düzgün sürekliliğin kullanışlı fakat basit bir
karakterizasyonu aşağıdaki teorem ile verilmektedir (Bu sonuç sınırsız aralıklar
için geçerli değildir).
94
Teorem 3.4.6. a < b ve f : (a, b) → R olsun. f fonksiyonunun (a, b) üzerinde
düzgün sürekli olması için gerek ve yeter şart f ’in [a, b] kapalı aralığına sürekli
genişletilebilmesi, yani
f (x) = g(x), x ∈ (a, b)
(3.11)
eşitliğini sağlayan bir g : [a, b] → R sürekli fonksiyonunun var olmasıdır.
Kanıt. f fonksiyonu (a, b) üzerinde düzgün sürekli olsun. Diğer taraftan n → ∞
iken b değerine yakınsayan bir xn ∈ (a, b) dizisi göz önüne alınsın. Buna göre
{xn } bir Cauchy dizisi olduğundan Lemma 3.4.4’e göre {f (xn )}’de bir Cauchy
dizisidir ve ayrıca
g(b) := lim f (xn )
n→∞
limiti vardır. Bu değer b değerine yaklaşan başka diziler kullanılsa da değişmez.
n → ∞ iken b değerine yakınsayan bir başka yn ∈ (a, b) dizisi göz önüne alınsın.
ε > 0 sayısı verilsin ve E = (a, b) için (3.9) ifadesini gerçekleyecek şekilde bir
δ > 0 sayısı seçilsin. xn − yn → 0 olduğundan n ≥ N için |xn − yn | < δ
eşitsizliğini gerçekleyecek şekilde N ∈ N sayısı seçilebilir. Dolayısıyla (3.9)’a
göre her n ≥ N için |f (xn ) − f (yn )| < ε sağlanır. Her ε > 0 için bu ifadenin
n → ∞ iken limiti alınırsa
| lim f (xn ) − lim f (yn )| ≤ ε
n→∞
n→∞
elde edilir. Bu ise Teorem 1.2.9’ya göre
lim f (xn ) = lim f (yn )
n→∞
n→∞
demektir. Benzer şekilde hareket ederek g(a) için istenilen gösterilebilir.
Her x ∈ (a, b) için g(x) = f (x) olsun. Buna göre g fonksiyonu [a, b] üzerinde tanımlıdır ve (3.11) ifadesini sağlar. Ayrıca Limitlerin Dizisel Karakterizasyonu’na göre [a, b] üzerinde süreklidir. Dolayısıyla, g’ye istenildiği şekilde
“sürekli genişletilebilir”.
Tersine, [a, b] üzerinde sürekli ve (3.11) ifadesini sağlayan bir fonksiyon g
olsun. Teorem 3.4.5’e göre [a, b] aralığı üzerinde g fonksiyonu düzgün süreklidir.
Dolayısıyla, g fonksiyonu (a, b) aralığı üzerinde düzgün süreklidir. Bu ise f ’in
(a, b) üzerinde düzgün sürekli olduğu anlamına gelir.
Sınırlı, açık ve dejenere olmayan (a, b) aralığında f fonksiyonu sürekli olsun.
Dikkat edilirse f ’in [a, b] aralığına sürekli genişletilebilmesi için gerek ve yeter
f fonksiyonunun tek-yönlü limitlerinin var ve a ve b sayılarına eşit olmasıdır.
Aslında, limitlerin varlığı durumunda her zaman g fonksiyonunun a ve b noktalarındaki değerleri söz konusu limitlere eşit olacak şekilde tanımlanabilir. Buna
göre f fonksiyonunun düzgün sürekliliğini ε ve δ argümanlarını kullanılmadan
göstermek mümkündür.
95
Örnek 3.4.7. (0, 1) üzerinde f (x) = (x − 1)/ log x fonksiyonunun düzgün
sürekli olduğunu gösteriniz.
Kanıt. Açıkça x → 0+ iken f (x) → 0 sağlanır. Diğer taraftan l’Hôpital Kuralı’na göre
x−1
1
lim f (x) = lim
= lim
=1
x→1−
x→1− log x
x→1− 1/x
elde edilir. Yani f (x) fonksiyonunun 0 noktasında sağdan ve 1 noktasında soldan limitleri mevcut olduğundan f fonksiyonu [0, 1] aralığına sürekli genişletilebilir. Dolayısıyla Teorem 3.4.6’ya göre f fonksiyonu (0, 1) aralığında düzgün
süreklidir.
Alıştırmalar
3.4.1. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu
tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) Eğer f fonksiyonu (0, ∞) aralığında düzgün sürekli ve g fonksiyonu (0, ∞) aralığında pozitif ve sınırlı ise f g fonksiyonu da (0, ∞) aralığında düzgün süreklidir.
b) x log(1/x) fonksiyonu (0, 1) aralığında düzgün süreklidir.
c) Her sıfırdan farklı m, b ∈ R için
cos x
mx + b
şeklinde tanımlanan fonksiyon (0, 1) üzerinde düzgün süreklidir.
d) f ve g fonksiyonları [a, b] üzerinde düzgün sürekli ve her x ∈ [a, b] için g(x) 6= 0
ise f /g fonksiyonu da [a, b] üzerinde düzgün süreklidir.
3.4.2. Tanım 3.4.1’i kullanarak aşağıda verilen fonksiyonların (0, 1) aralığında düzgün sürekli olduğunu gösteriniz.
a) f (x) = x2 + x
b) f (x) = x3 − x + 2
c) f (x) = x sin x
3.4.3. Aşağıda verilen fonksiyonların (0, 1) aralığında düzgün sürekli olduğunu gösteriniz (sin x ve cos x fonksiyonlarının tanım bölgeleri üzerinde sürekli olduğu bilindiğine
göre isteneni göstermek için l’Hôpital Kuralı kullanılabilir).
a) f (x) =
sin x
x
b) f (x) = x cos
1
x2
c) f (x) = x log x
d) f (x) = (1 − x2 )1/x
3.4.4. sin x fonksiyonunun R üzerinde sürekli olduğu bilindiğine göre (0, 1) açık aralığı
üzerinde xα sin(1/x) fonksiyonunun düzgün sürekli olduğu α reel sayısını tespit ediniz.
96
a) f : [0, ∞) fonksiyonu sürekli ve x → ∞ iken f (x) → L olacak şekilde
bir L ∈ R sayısı var olsun. Buna göre f fonksiyonunun [0, ∞) üzerinde düzgün
sürekli olduğunu ispatlayınız.
b) f (x) = 1/(x2 +1) fonksiyonunun R üzerinde düzgün sürekli olduğunu gösteriniz.
3.4.5.
3.4.6. Reel sayıların boştan farklı bir alt kümesi E, α ∈ R ve f, g : E → R fonksiyonları E üzerinde düzgün sürekli olsun. α
a) f +g ve αg fonksiyonlarının da E üzerinde düzgün sürekli olduğunu ispatlayınız.
b) f ve g fonksiyonları E üzerinde sınırlı ise f g fonksiyonun E üzerinde düzgün
sürekli olduğunu gösteriniz.
c) f g çarpım fonksiyonu R üzerinde düzgün sürekli olmadığı halde R üzerinde
düzgün sürekli olan f ve g fonksiyonlarının varlığını gösteriniz.
d) f fonksiyonu E üzerinde sınırlı ve her x ∈ E için g(x) ≥ ε0 eşitsizliğini sağlayacak şekilde bir ε > 0 sayısı var olsun. Buna göre f /g fonksiyonunun E üzerinde
düzgün sürekli olduğunu ispatlayınız.
e) Her x ∈ (0, 1) için g(x) > 0 olmak üzere f /g bölüm fonksiyonu (0, 1) üzerinde düzgün sürekli olmadığı halde (0, 1) üzerinde düzgün sürekli olan f ve g
fonksiyonlarının varlığını gösteriniz.
a) I bir sınırlı aralık olsun. Eğer f : I → R fonksiyonu I üzerinde düzgün
sürekli ise f ’in I üzerinde sınırlı olduğunu ispatlayınız.
b) a) şıkkında verilen ifadede I sınırsız veya sadece f sürekli olarak alınır ise
sınırlılık hakkında verilen hüküm doğru olmayabilir.
3.4.7.
3.4.8. E ⊆ R olsun. f : E → R fonksiyonunun E üzerinde artan olarak adlandırılması
için gerek ve yeter şart x1 < x2 koşulunu sağlayan her x1 , x2 ∈ E için f (x1 ) ≤ f (x2 )
eşitsizliğinin gerçeklenmesidir. f fonksiyonu boştan farklı, sınırlı ve açık (a, b) aralığı
üzerinde artan olsun.
a) f (a+) ve f (a−) limitlerinin her ikisinin de var ve sonlu olduğunu ispatlayınız.
b) Gösteriniz ki f fonksiyonunun (a, b) aralığında sürekli olması için gerek ve yeter
şart f ’in (a, b) üzerinde düzgün sürekli olmasıdır.
c) Gösteriniz ki eğer f sınırsız ise b) şıkkı doğru değildir. Yani, (0, 1) aralığı üzerinde sürekli fakat bu aralık üzerinde düzgün sürekli olmayan bir g : (0, 1) → R
fonksiyonu vardır.
3.4.9. İspatlayınız ki n. dereceden bir polinomun R üzerinde sürekli olması için gerek
ve yeter şart n = 0 ya da 1 olmasıdır.
97
4 R Üzerinde Diferansiyellenebilme
4.1
Türev
Tanım 4.1.1. Reel değerli bir f fonksiyonunun bir a noktasında diferansiyellenebilir olarak adlandırılması için gerek ve yeter şart f fonksiyonunun a
noktasını içeren bir I açık aralığında tanımlı ve
f ′ (a) := lim
h→0
f (a + h) − f (a)
h
(4.1)
limitinin var olmasıdır. Bu durumda f ′ (a) değerine a noktasında f fonksiyonunun türev i denir.
f fonksiyonu a noktasını içeren bir I açık aralığı üzerinde tanımlı olduğundan yeterince küçük h 6= 0 için (4.1) ile verilen bölüm de tanımlıdır.
Biliyoruz ki y = f (x) fonksiyonunun bir (a, f (a)) noktasında düşey olmayan
bir teğet doğrusunun (veya tanjat doğrusu) olması için gerek ve yeter şart f ’in
a noktasında türevi olmasıdır. Bu durumda x = a noktasında fonksiyonun
graﬁğine çizilen teğetin eğimi f ′ (a)’dır. Bu bağlantının mantıklı olduğunu gözlemlemek için (4.1) ifadesinin geometrik yorumunu verelim: f fonksiyonu a
noktasında diferansiyellenebilir olsun. y = f (x) eğrisinin graﬁği üzerindeki en
az iki noktadan geçen doğruya secant doğrusu (veya kesen), eğrinin graﬁği
üzerindeki bir noktadan yine eğrinin üzerinde ki diğer bir noktaya çizilen doğru
parçasına ise kiriş adı verilir. x = a + h olsun. Buna göre (x, f (x)) ve (a, f (a))
noktalarından geçen kirişin eğimi (f (x)−f (a))/(x−a)’dır. x = a+h olduğundan
(4.1) ifadesinden
f (x) − f (a)
f ′ (a) := lim
x→a
x−a
yazılabilir. x → a olduğundan aşağıdaki şekilde de görüldüğü üzere (x, f (x))
ve (a, f (a)) noktalarından geçen kirişlerin eğimi, x = a noktasından y = f (x)
doğrusuna çizilen teğetin eğimine yaklaşmaktadır ve limit durumunda x = a
noktasında y = f (x) eğrisine çizilen teğet doğrusunun eğimi tam olarak f ′ (a)
değerine eşittir. Buna göre x = a noktasında y = f (x) eğrisinin graﬁğinin
(a, f (a)) noktasında tek türlü belirli bir teğet doğrusuna sahip olabilmesi için
gerek ve yeter şart f ′ (a) türevinin var olmasıdır denir.
y
y = f (x)
Kirişler
.
.
Teğet
.
a
x2
x1
x
f fonksiyonu E kümesi üzerindeki tüm noktalarda diferansiyellenebilir ise
f ′ türev fonksiyonu E üzerinde bir fonksiyondur. Bu fonksiyon pek çok şekilde
gösterilebilir:
df
= f (1) = f ′ .
Dx f =
dx
y = f (x) olması durumunda f ′ için dy/dx veya y ′ noktasyonları kullanılır. Yüksek mertebeden türevler rekürsif olarak tanımlanır: yani, söz konusu türevlerin
var olması durumunda n ∈ N için f (n+1) (a) := (f (n) )′ (a)’dır. Ayrıca, yüksek
mertebeden türevleri ifade etmek için de çeşitli yollar kullanılır: Dxn f , dn f /dxn
ve f (n) gibi. Eğer y = f (x) ise dn y/dxn veya y (n) yazılır. f (2) (sırası ile, y (2) )
ikinci türev i fonksiyonu f ′′ (sırası ile, y ′′ ) ile gösterilir ve bir a noktasında var
olması durumunda f fonksiyonu a noktasında iki kez diferansiyellenebilir dir
denir.
Türevlerle çalışma söz konusu olduğundan diferansiyellenebilmenin iki karakterizasyonunu verebiliriz. Bunlardan ilki türevleri
F (x) :=
f (x) − f (a)
, x 6= a
x−a
(4.2)
“kiriş fonksiyonu” ile karakterize etmektir. Bu metot Zincir Kuralı’nı ortaya
koyarken kullanılacaktır.
Teorem 4.1.2. Reel değerli f fonksiyonunun bir a ∈ R noktasında diferansiyellenebilmesi için gerek ve yeter şart a ∈ I, I üzerinde tanımlı bir fonksiyon
f , a noktasında sürekli bir fonksiyon F ve her x ∈ I için
f (x) = F (x)(x − a) + f (a)
(4.3)
eşitliğinin sağlandığı bir I açık aralığı ve F : I → R fonksiyonunun var olmasıdır. Bu durumda F (a) = f ′ (a) gerçeklenir.
Kanıt. Dikkat edilirse her x ∈ I\{a} için (4.2) and (4.3) ifadeleri birbirlerine
denktir. f fonksiyonu a noktasında diferansiyellenebilir olsun. Buna göre f
fonksiyonu a noktasını içeren bir I açık aralığında tanımlıdır ve (4.1) ifadesinde
100
verilen limit vardır. F fonksiyonu I üzerinde x 6= a olması durumunda (4.2)
eşitliği ile, a noktasında ise F (a) := f ′ (a) olarak tanımlansın. Dolayısıyla, her
x ∈ I için (4.3) eşitliği gerçeklenir ve f ′ (a) türevi var olduğundan (4.2)’ye göre
F fonksiyonu süreklidir.
Tersine (4.3) ifadesi gerçeklensin. Buna göre her x 6= a, x ∈ I için (4.2)
eşitliği sağlanır. x → a iken (4.2) ifadesinden limit alınırsa, F ’in a noktasında
sürekli olduğu bilindiğine göre, F (a) = f ′ (a) elde edilir.
Diferansiyellenebilmenin ikinci karakterizasyonu ise lineer yaklaşım (f (a +
h) − f (a)’ya orijinden geçen doğrular ile ne kadar iyi yaklaşılabilir) ile verilir.
Bu olgu çok değişkenli fonksiyonların türevleri tanımlanırken kullanılacaktır.
Teorem 4.1.3. Reel değerli f fonksiyonunun bir a noktasında diferansiyellenebilmesi için gerek ve yeter şart T (x) := mx fomundaki bir T fonksiyonunun
lim
h→0
f (a + h) − f (a) − T (h)
=0
h
(4.4)
eşitliğini sağlayacak şekilde var olmasıdır.
Kanıt. f fonksiyonu türevlenebilir ve m := f ′ (a) olsun. Dolayısıyla (4.1)’e göre
h → 0 iken
f (a + h) − f (a) − T (h)
f (a + h) − f (a)
=
− f ′ (a) → 0
h
h
gerçeklenir.
Tersine, h 6= 0 ve T (x) := mx için (4.4) ifadesi sağlansın. Buna göre
f (a + h) − f (a) − mh
f (a + h) − f (a)
=m+
h
h
f (a + h) − f (a) − mh
=m+
h
ifadesinden limit alınırsa (4.4)’e göre m elde edilir. Dolayısıyla, h → 0 iken
(f (a + h) − f (a))/h → m sonucuna ulaşılır. Yani, f ′ (a) türevi vardır ve m’e
eşittir.
Teorem 4.1.2’nin aşağıda verilen ilk uygulaması süreklilik ile diferansiyellenebilme arasındaki ilişkiyi ortaya koymaktadır.
Teorem 4.1.4. f fonksiyonu a noktasında diferansiyellenebilir ise aynı zamanda bu noktada süreklidir.
Kanıt. f fonksiyonu a noktasında diferansiyellenebilir olsun. Teorem 4.1.2’ye
göre her x ∈ I için f (x) = f (a) + F (x)(x − a) şeklinde tanımlı, a noktasında
101
sürekli bir F fonksiyonu ve I açık aralığı vardır. Bu ifadeden x → a iken limit
alınırsa
lim f (x) = f (a) + F (x) · 0 = f (a)
x→a
elde edilir. Yani, x → a iken f (x) → f (a) sonucuna ulaşılır ki bu f fonksiyonu
a noktasında sürekli demektir.
Yukarıdaki teoreme göre a noktasında sürekli olmayan hiç bir fonksiyon a’da
diferansiyellenebilir değildir. Örnek 4.1.5, Teorem 4.1.4’ün tersinin, yani bir a
noktasında sürekli olan fonksiyonların bu a noktasında diferansiyellenmesini
gerektirmediğini göstermektedir.
Örnek 4.1.5. f (x) = |x| fonksiyonunun 0 noktasında sürekli fakat diferansiyellenebilir olmadığını gösteriniz.
Kanıt. Mutlak değer fonksiyonunun tanımına göre x → 0 iken |x| → 0 sağlandığından f fonksiyonu 0 noktasında süreklidir. h > 0 iken |h| = h ve h < 0 iken
|h| = −h sağlandığından
lim
h→0+
ve
lim
h→0−
h−0
f (0 + h) − f (0)
= lim
=1
h→0+
h
h
f (0 + h) − f (0)
−h − 0
= lim
= −1
h→0−
h
h
elde edilir. Limitin var olması için tek-yönlü limitlerin mevcut ve birbirine eşit
olması gerektiğinden (Teorem 3.2.3), a = 0 ve f (x) = |x| için (4.1) ifadesindeki
limit yoktur. Buna göre f fonksiyonu 0 noktasında diferansiyellenebilir değildir.
y
y = |x|
.
x
Aslında Örnek 4.1.5 diferansiyellenebilme ve sürekli fonksiyonlar arasındaki
fark hakkında ki en genel yanlış anlaşılmayı yansıtır. a noktasında diferansiyellenebilen bir fonksiyon (a, f (a)) noktasında daima tek türlü belirli bir teğet
102
doğrusuna sahip olacağından, verilen bir aralıkta bu diferansiyellenebilir fonksiyonun graﬁği “düzgün”dür, yani bir köşe, bir sivri uç veya kırılma noktası
içermez. Aksine, her ne kadar bir sürekli fonksiyonun graﬁği verilen bir aralıkta kesintisiz (boşluk veya sıçrama içermeyen) olsa da bir köşe, bir sivri uç
veya bir kırılma noktası içerebilir. Özel olarak, x = 0 noktasında f (x) = |x|
fonksiyonu sürekli olmakla birlikte diferansiyellenebilir değildir. Ayrıca, y = |x|
graﬁği her ne kadar kesintisiz olsa da (0, 0)’da bir köşe içerir.
Tanım 4.1.1’e göre f fonksiyonu a noktasında diferansiyellenebilir ise f ’in
a noktasını (dolayısıyla a’nın her iki yanını da) içeren bir açık aralık ğzerinde
tanımlanmış olması gerekir. Limit kavramındaki gibi tanım bölgesi kapalı aralıklar olan fonksiyonlar için “tek-yönlü” türevlerini tanımlamak uygun olur (bkz
Örnek 4.1.9). Burada bir reel fonksiyonun bir aralık üzerinde diferansiyellenebilmesi ne anlama gelir kısaca vurgulanmaktadır (bir aralık içindeki her noktada diferansiyellenebilmenin tersine). Bu konsept İntegral kavramı anlatılırken
kullanılacaktır.
Tanım 4.1.6. I dejenere olmayan bir aralık olsun.
i) Bir f : I → R fonksiyonunun I aralığı üzerinde diferansiyellenebilir olarak adlandırılması için gerek ve yeter şart
fI′ (a) := x→a
lim
x∈I
f (x) − f (a)
x−a
limitinin mevcut ve her a ∈ I için sonlu olmasıdır.
ii) f fonksiyonunun I üzerinde sürekli diferansiyellenebilir olarak adlandırılması için gerek ve yeter şart fI′ türevinin mevcut ve I üzerinde sürekli
olmasıdır.
Dikkat edilirse, I aralığının bir uç noktası a değil iken fI′ (a) ile f ′ (a) değerleri aynıdır. Bu durumda genellikle fI′ notasyonundaki alt indis kullanılmaz.
Ayrıca, f fonksiyonu [a, b] aralığında diferansiyellenebilir ise
f (b + h) − f (b)
f (a + h) − f (a)
vef ′ (b) := lim
h→0−
h→0+
h
h
f ′ (a) := lim
ifadeleri yazılabilir.
Örnek 4.1.7.
yınız.
i) Her x ∈ R ve n ∈ N için (xn )′ = nxn−1 olduğunu ispatla-
ii) Her x ∈ (0, ∞) ve n ∈ −N∪{0} için (xn )′ = nxn−1 olduğunu ispatlayınız.
Kanıt. i) Her c, d ∈ R ve n ∈ N için
cn − dn = (c − d) (cn−1 + cn−2 d + cn−3 d2 + · · · + cdn−2 + dn−1 )
|
{z
}
n terim
103
şeklinde yazılabileceğini biliyoruz. f (x) = xn olsun. n = 1 ise her a ∈ R için
f ′ (a) = lim
x→a
f (x) − f (a)
x−a
= lim
=1
x→a x − a
x−a
elde edilir. Eğer n > 1 ve x 6= a ise
f (x) − f (a)
x n − an
= lim
x→a
x→a x − a
x−a
(x − a)(xn−1 + xn−2 a + xn−3 a2 + · · · + xan−2 + an−1 )
= lim
x→a
x−a
n−1
n−2
n−3 2
= lim (x
+x
a+x
a + · · · + xan−2 + an−1 )
f ′ (a) = lim
x→a
= (an−1 + an−2 a + an−3 a2 + · · · + aan−2 + an−1 )
{z
}
|
n terim
= na
n−1
sonucuna ulaşılır.
ii) f (x) = xn olsun. n = 0 ise f (x) = x0 = 1 olduğundan her x ∈ R için
f ′ (a) = lim
x→a
f (x) − f (a)
1−1
= lim
=0
x→a
x−a
x−a
elde edilir. n ∈ −N ve a > 0 olsun. Bu durmda −n ∈ N olduğundan i) şıkkı
kullanılarak
f (x) − f (a)
x n − an
= lim
x→a
x→a x − a
x−a
a−n − x−n n n
= lim
x a
x→a
x−a
−n
a − x−n
lim (xn an )
= lim
x→a
x→a
x−a
f ′ (a) = lim
= na−n−1 a2n
= nan−1
elde edilir. Buna göre xn fonksiyonu a ∈ R noktasında diferansiyellenebilirdir
ve türevi f ′ (a) = nan−1 ’e eşittir.
Örnek 4.1.8.
i) n ∈ Z ve n ∈ N olmak üzere q = n/m ise
xn − an = (xq − aq )(xq(m−1) + x2(m−2) aq + · · · + xq aq(m−2) + aq(m−1) )
eşitliğinin gerçeklendiğini gösteriniz.
ii) [Kuvvet Kuralı] Her q ∈ Q için xq fonksiyonunun (0, ∞) aralığında diferansiyellenebilir ve (xq )′ = qxq−1 olduğunu ispatlayınız.
104
Kanıt. i) Örnek 4.1.7’de söylendiği üzere her c, d ∈ R ve m ∈ N için
cm − dm = (c − d) (cm−1 + cm−2 d + cm−3 d2 + · · · + cdm−2 + dm−1 )
{z
}
|
m terim
eşitliği geçerlidir. Burada q = n/m olmak üzere c = xq ve d = aq alınır istenilen
gösterilmiş olur.
ii) f (x) = xq , x, a ∈ (0, ∞) ve q = n/m olsun. i) şıkkı kullanılarak
f (x) − f (a)
x q − aq
= lim
x→a
x→a x − a
x−a
n
n
x −a
= lim
(xq(m−1) + · · · + aq(m−1) )−1
x→a x − a
n
x − an
lim (xq(m−1) + · · · + aq(m−1) )−1
= lim
x→a
x→a
x−a
|
{z
}
f ′ (a) = lim
m terim
= na
n−1
(ma
q(m−1) −1
)
= qa
n−1−qm+q
= qaq−1
elde edilir.
Aşağıdaki örnek Tanım 4.1.6’nın sürekli fonksiyonların ailelerine genişletilebileceğini ortaya koyar.
Örnek 4.1.9. f (x) = x3/2 fonksiyonu [0, ∞) aralığında diferansiyellenebilirdir
√
ve türevi her x ∈ [0, ∞) için f ′ (x) = 3 x/2’ye eşittir.
Kanıt. Kuvvet Kuralı’na (Örnek 4.1.8) göre her x ∈ (0, ∞) için
f ′ (x) = (x3/2 )′ =
3
3√
3 (3/2)−1
x
x
= x1/2 =
2
2
2
sağlanır. Ayrıca, tanıma göre
√
h3/2 − 0
f (0 + h) − f (0)
= lim
= lim h = 0
h→0+
h→0+
h→0+
h
h
f ′ (0) = lim
gerçeklenir.
Tanım 4.1.6 ile bağlantılı olarak sıklıkla kullanılan bir notasyon verelim. I
dejenere olmayan bir aralık olsun. Her n ∈ N için C n fonksiyonlar ailesini
C n (I) := {f : f : I → R ve f (n) türevi var ve türev I üzerinde sürekli}
olarak tanımlayalım. Her n ∈ N için C n (I)’ya ait olan f fonksiyonlarının ailesi
C ∞ (I) ile gösterilir. Dikkat edilir ise C 1 (I) notasyonu I üzerinde sürekli diferansiyellenebilen reel değerli fonksiyonların ailesini gösterir. Üzerinde çalışılan
aralık açık olarak verildiğinde bu notasyonda dışarıdaki parantezler ihmal edilecektir. Yani C n ([a, b]) yerine C n [a, b] yazımı kullanılacaktır.
105
Teorem 4.1.4 modiﬁye edilerek bir I aralığı üzerinde diferansiyellenebilir bir
fonksiyonun I aralığı üzerinde sürekli olduğu sonucu elde edilebilir. Dolayısıyla,
her m > n > 0 tamsayıları için C ∞ (I) ⊂ C m (I) ⊂ C n (I) içermesi doğrudur.
Aşağıdaki örnekte R üzerinde her diferansiyellenebilir fonksiyonun C 1 (R)
ailesine ait olmadığı gösterilmektedir.
Örnek 4.1.10.
f (x) =

x2 sin(1/x)
0
x 6= 0
x=0
şeklinde tanımlanan fonksiyon R üzerinde süreklidir. Fakat orijin noktasını içeren hiç bir reel sayı aralığında sürekli diferansiyellenebilir değildir.
Kanıt. Tanıma göre
h2 sin(1/h) − 0
f (0 + h) − f (0)
= lim
= lim h sin(1/h) = 0
h→0
h→0
h→0
h
h
f ′ (0) = lim
ve x 6= 0 için
f ′ (x) = 2x sin(1/x) − cos(1/x)
olduğundan f fonksiyonu R’de diferansiyellenebilirdir, fakat limx→0 f ′ (x) limiti
yoktur. Buna göre f ′ fonksiyonu orijin noktasını içeren hiç bir aralıkta sürekli
değildir.
İki farklı aralık üzerinde diferansiyellenebilen bir fonksiyonunun bu iki aralığın birleşimi üzerinde diferansiyellenebilir olması gerekmez.
Açıklama 4.1.11. f (x) = |x| fonksiyonu [0, 1] ve [−1, 0] aralıkları üzerinde
diferansiyellenebilir iken [−1, 1] aralığı üzerinde diferansiyellenemez.
Kanıt. x > 0 iken f (x) = x ve x < 0 iken f (x) = −x olduğundan açıkça f
fonksiyonu [−1, 0) ∪ (0, 1] aralığında diferansiyellebenilir (x > 0 ise f ′ (x) = 1
ve x < 0 ise f ′ (x) = −1). Örnek 4.1.5’den biliyoruz ki f (x) fonksiyonu x = 0
noktasında diferansiyellenebilir değildir. Bununla beraber
|h|
|h|
′
= 1 ve f[−1,0]
= −1
(0) = lim
h→0− h
h→0+ h
′
f[0,1]
(0) = lim
olduğundan f fonksiyonu [0, 1] ve [−1, 0] aralıkları üzerinde diferansiyellenebilirdir.
106
Alıştırmalar
4.1.1. f, g : [a, b] → R olsun. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu tespit ediniz. Doğru olanları ispatlayıp yanlış olanlara ise birer
ters örnek veriniz.
a) Eğer f = g 2 ve [a, b] aralığında f diferansiyellenebilir ise (a, b) aralığında g
diferansiyellenebilirdir.
b) Eğer [a, b] aralığında f diferansiyellenebilir ise [a, b] üzerinde düzgün süreklidir.
c) Eğer (a, b) aralığında f (a) = f (b) = 0 ise f fonksiyonu [a, b] üzerinde düzgün
süreklidir.
d) Eğer f fonksiyonu (a, b] aralığında diferansiyellenebilir ve x → a+ iken f (x)/(x−
a) → 1 ise f fonksiyonu (a, b] üzerinde düzgün süreklidir.
4.1.2. Aşağıdaki her reel fonksiyon için Tanım 4.1.1’i kullanarak f ′ (a) tğrevinin var
olduğunu gösteriniz.
2
a) f (x) = x
√ + x, a ∈ R
b) f (x) = x, a > 0
c) f (x) = 1/x, a 6= 0
4.1.3.
fα (x) =

|x|α 1
x
0
x 6= 0
x=0
olsun. α > 0 ise x = 0 noktasında fα (x) fonksiyonunun sürekli ve α > 1 için x = 0
noktasında diferansiyellenebilir olduğunu gösteriniz.
4.1.4. 0 noktasını içeren bir aralık I ve f : I → R olsun. Her x ∈ I için |f (x)| ≤ |x|α
eşitsizliğini gerçekleyecek α > 1 sayısı varsa f fonksiyonunun 0 noktasında diferansiyellenebilir olduğunu ispatlayınız.α = 1 olması durumunu inceleyiniz.
a) y = x+sin x eğrisinin y = x+15 doğrusuna paralel olan tüm teğetlerinin
y = x + sin x eğrisini kestiği yerlerin koordinatlarını belirleyiniz.
b) y = 3x2 + 2 eğrisine teğet olan ve (−1, 7) noktasından geçen tüm teğtlerinin
y = 3x2 + 2 eğrisini kestiği yerlerin koordinatlarını belirleyiniz.
4.1.5.
4.1.6. f fonksiyonu R üzerinde
fα (x) :=

 x3
0
x≥0
x<0
olarak tanımlansın. Her R için f (n) var olmasını sağlayan tüm n ∈ N değerlerini tespit
ediniz.
4.1.7. f : (0, ∞) → R fonksiyonu her x, y ∈ (0, ∞) için f (x) − f (y) = f (x, y) ve
f (1) = 0 koşullarını sağlasın.
a) f fonksiyonunun (0, ∞) aralığında sürekli olması için gerek ve yeter şart 1
noktasında sürekli olmasıdır, ispatlayınız.
b) f fonksiyonunun (0, ∞) aralığında diferansiyellenebilir olması için gerek ve yeter
şart 1 noktasında diferansiyellenebilir olmasıdır, ispatlayınız.
107
c) Gösteriniz ki, f fonksiyonu 1 noktasında diferansiyellenebilir ise her x ∈ (0, ∞)
için f ′ (x) = f ′ (1)/x’dir.
[Not: Eğer f ′ (1) = 1 ise f (x) = log x fonksiyonudur.]
4.1.8. I bir açık aralık, f : I → R ve c ∈ I olsun. f fonksiyonunun c noktasında yerel
maksimumu vardır olarak isimlendirilmesi için gerek ve yeter şart her |x − c| < δ için
f (c) ≥ f (x) eşitsizliğini sağlayacak şekilde bir δ > 0 sayısının var olmasıdır.
a) c noktasında f fonksiyonunun yerel maksimumu varsa u > 0 ve yeterince küçük
t < 0 için
f (c + t) − f (c)
f (c + u) − f (c)
≤ 0 ve
≥0
u
t
eşitsizliklerinin sağlandığını gösteriniz.
b) Yukarıdaki ifadeyi yerel minimum için yazınız.
c) Gösteriniz ki, f fonksiyonu 1 noktasında diferansiyellenebilir ise her x ∈ (0, ∞)
için f ′ (x) = f ′ (1)/x’dir.
d) b) ve c) şıklarındaki ifadelerin terslerinin doğru olmadığını bir örnek ile gösteriniz: 0 noktasında yerel maksimum ve yerel minimum içermediği halde f ′ (0) = 0
sağlayan bir f fonksiyonu bulunuz.
4.1.9. a > 0 için (−a, a) olsun. Bir f : I → R fonksiyonunun çift olarak isimlendirimesi için gerek ve yeter şart her x ∈ I için f (−x) = f (x) eşitliğinin, tek olarak
isimlendirimesi için gerek ve yeter şart her x ∈ I için f (−x) = −f (x) eşitliğinin
sağlanmasıdır.
a) Eğer f fonksiyonu tek ve I üzerinde diferansiyellenebilir ise I üzerinde f ′ türev
fonksiyonunun çift olduğunu gösteriniz.
b) Eğer f fonksiyonu çift ve I üzerinde diferansiyellenebilir ise I üzerinde f ′ türev
fonksiyonunun tek olduğunu gösteriniz.
4.2
Diferansiyellenebilme Teoremleri
Teorem 4.2.1. f ve g reel fonksiyonlar ve α ∈ R olsun. Eğer f ve g fonksiyonları a noktasında diferansiyellenebilir ise f +g, αf , f ·g ve (g(a) 6= 0 olması
durumunda) f /g fonksiyonları da a noktasında diferansiyellenebildir. Ayrıca
ve
eşitlikleri sağlanır.
(f + g)′ (a) = f ′ (a) + g ′ (a),
(4.5)
(αf )′ (a) = αf ′ (a),
(4.6)
(f · g)′ (a) = g(a)f ′ (a) + f (a)g ′ (a),
(4.7)
′
g(a)f ′ (a) − f (a)g ′ (a)
f
(a) =
g
g 2 (a)
(4.8)
108
Kanıt. Yukarıdaki ifadelerin doğruluğunu göstermek için yapılan ispat tarzları
aynı olduğundan biz burada sadece (4.7)’nin açık kanıtını vereceğiz. Buna göre
f (x)g(x) − f (a)g(a) + f (a)g(x) − f (a)g(x)
f (x)g(x) − f (a)g(a)
=
x−a
x−a
g(x)(f (x) − f (a)) + f (a)(g(x) − g(a))
=
x−a
g(x) − g(a)
f (x) − f (a)
+ f (a)
= g(x)
x−a
x−a
yazılabilir. Yukarıdaki ifade fonksiyonların çarpımıdır. g fonksiyonu sürekli olduğundan (bkz Teorem 4.1.4), Tanım 4.1.1 and Teorem 3.1.10’a göre
f (x)g(x) − f (a)g(a)
g(x) − g(a)
f (x) − f (a)
lim
+ lim f (a)
= lim g(x)
x→a
x→a
x→a
x−a
x−a
x−a
f (x) − f (a)
g(x) − g(a)
= lim g(x) lim
+ lim f (a)
x→a
x→a
x→a
x−a
x−a
= g(a)f ′ (a) + f (a)g ′ (a)
elde edilir.
Formül (4.5)’e Toplam Kuralı, (4.6)’ya Homojenlik Kuralı, (4.7)’ye Çarpım
Kuralı ve (4.8)’e ise Bölüm Kuralı adı verilir.
İki fonksiyonun bileşkesinin türevi hakkında aşağıdaki teorem söz konusudur.
Teorem 4.2.2 (Zincir Kuralı). f ve g reel değerli iki fonksiyon olsun. Eğer
f fonksiyonu a noktasında, g fonksiyonu f (a) noktasında diferansiyellenebilir
iseg ◦ f fonksiyonu da a noktasında diferansiyellenebilirdir ve
(g ◦ f )′ (a) = g ′ (f (a))f ′ (a)
sağlanır.
Kanıt. Teorem 4.1.2’ye göre açık I ve J aralıkları, a noktasında sürekli F : I →
R, f (a) noktasında sürekli G : I → R fonksiyonları F (a) = f ′ (a), G(f (a)) =
g ′ (f (a)),
f (x) = F (x)(x − a) + f (a), x ∈ I
(4.9)
ve
g(y) = G(y)(y − f (a)) + g(f (a)), y ∈ J
(4.10)
ifadelerini sağlayacak şekilde mevcuttur. f fonksiyonu a noktasında sürekli olduğundan her x ∈ I için f (x) ∈ J olduğunu varsayabiliriz (eğer gerekirse I
aralığı küçültülebilir).
109
Bir x ∈ I sabitlensin. (4.10) eşitliğinde y = f (x) alınır ve bu ifadede (??)
kullanılır ise
(g ◦ f )(x) = g(f (x)) = G(f (x))(f (x) − f (a)) + g(f (a))
= G(f (x))F (x)(x − a) + (g ◦ f )(a)
elde edilir. Her x ∈ I için H(x) = G(f (x))F (x) olsun. a noktasında F fonksiyonu ve f (a) noktasında G fonksiyonu sürekli olduğundan H fonksiyonu da a
noktasında süreklidir. Ayrıca,
H(a) = G(f (a))F (a) = g ′ (f (a))f ′ (a)
sağlanır. Buna göre Teorem 4.1.2 kullanılarak (g ◦ f )′ (a) = g ′ (f (a))f ′ (a) eşitliğine ulaşılır.
Alıştırmalar
4.2.1. a noktasını içeren bir açık aralık I ve f, g, h : I → R olsun. Aşağıda verilen ifadelerin hangilerinin doğru, hangilerinin yanlış olduğunu tespit ediniz. Doğru olanları
ispatlayıp yanlış olanlara ise birer ters örnek veriniz.
a) f, g ve h fonksiyonları a noktasında diferansiyellenebilir ise
(f gh)′ (a) = f ′ (a)g(a)h(a) + f (a)g ′ (a)h(a) + f (a)g(a)h′ (a)
sağlanır.
b) f fonksiyonu a noktasında iki kez diferansiyellenebilir ve g fonksiyonu f (a)
noktasında iki kez diferansiyellenebilir ise
(g ◦ f )′′ (a) = g ′ (f (a))f ′′ (a) + g ′′ (f (a))(f ′ (a))2
sağlanır.
c) f (n) (a) ve g (n) (a) ile verilen n. derece türevler var ise
(f + g)(n) (a) = f (n) (a) + g (n) (a)
sağlanır.
d) f (n) (a) ve g (n) (a) ile verilen n. derece türevler var ve sıfırdan farklı ise
(n)
g(a)f (n) (a) + (−1)n f (a)g (n) (a)
f
(a) =
g
g (n+1) (a)
sağlanır.
4.2.2. f ve g fonksiyonları 2 ve 3 noktalarında diferansiyellenebilir f ′ (2) = a, f ′ (3) =
b, g ′ (2) = c ve g ′ (3) = d
a) f, g ve h fonksiyonları a noktasında diferansiyellenebilir ise
(f gh)′ (a) = f ′ (a)g(a)h(a) + f (a)g ′ (a)h(a) + f (a)g(a)h′ (a)
sağlanır.
110
b) f fonksiyonu a noktasında iki kez diferansiyellenebilir ve g fonksiyonu f (a)
noktasında iki kez diferansiyellenebilir ise
(g ◦ f )′′ (a) = g ′ (f (a))f ′′ (a) + g ′′ (f (a))(f ′ (a))2
sağlanır.
c) f (n) (a) ve g (n) (a) ile verilen n. derece türevler var ise
(f + g)(n) (a) = f (n) (a) + g (n) (a)
sağlanır.
d) f (n) (a) ve g (n) (a) ile verilen n. derece türevler var ve sıfırdan farklı ise
(n)
g(a)f (n) (a) + (−1)n f (a)g (n) (a)
f
(a) =
g
g (n+1) (a)
sağlanır.
4.3
Bazı Fonksiyonların Türevleri
Bu noktaya kadar aşağıdaki türevlerin doğruluğu gösterilmiştir:
• f (x) = c (c sabit sayı) ise f ′ (x) = 0’dır
• f (x) = xq ise f ′ (x) = qxq−1 ’dir
• f (x) = |x| ise f ′ (x) =
x
|x| ’dir.
Şimdi bazı önemli fonksiyonların türevlerinin ne şekilde hasaplandığını inceleyelim.
Trigonometrik Fonksiyonların Türevleri
Teorem 4.3.1. Sinüs fonksiyonunun türevi kosinüs fonksiyonudur:
d
sin x = cos x.
dx
Kanıt. Türev tanımı, sinüs fonksiyonu için toplam formülü (sin(x+h) = sin x cos h+
cos x sin h) ve limit kuralları kullanılarak
d
sin(x + h) − sin x
sin x cos h + cos x sin h − sin x
sin x = lim
= lim
h→0
h→0
dx
h
h
sin x(cos h − 1) + cos x sin h
= lim
h→0
h
cos x sin h
sin x(cos h − 1)
+ lim
= lim
h→0
h→0
h
h
cos h − 1
sin h
= sin x lim
+ cos x lim
h→0
h→0
h
h
elde edilir.
= sin x · 0 + cos x · 1 = cos x.
111
Teorem 4.3.2. Kosinüs fonksiyonunun türevi negatif sinüs fonksiyonudur:
d
cos x = − sin x.
dx
Kanıt. Türev tanımı, kosinüs fonksiyonu için toplam formülü (cos(x + h) =
cos x cos h−sin x sin h) ve limit kuralları kullanılarak yukarıdaki şekilde hareket
ederek istenilen gösterilir. Diğer taraftan
π
π
− x = cos x ve cos
− x = sin x
sin
2
2
olduğundan Zincir Kuralı (Teorem 4.2.2) kullanılarak
π
π
d
d
cos x =
sin
− x = (−1) cos
− x = − sin x
dx
dx
2
2
türev değeri elde edilir.
Örnek 4.3.3. Aşağdaki fonksiyonların türevlerini hesaplayınız.
i) sin(πx) + cos(3x)
√
ii) x2 sin x
iii)
cos x
1−sin x
Çözüm. i) Toplam ve Zincir Kuralları kullanılarak
d
(sin(πx) + cos(3x)) = π cos(πx) − 3 sin(3x)
dx
elde edilir.
ii) Çarpım ve Zincir Kuralları kullanılarak
√
√
√
√
√ 1
d 2
1
(x sin x) = 2x sin x + x2 cos x √ = 2x sin x + x3/2 cos x
dx
2
2 x
elde edilir.
iii) Bölüm Kuralı kullanılarak
(1 − sin x)(− sin x) − (cos x)(0 − cos x)
cos x
d
=
dx 1 − sin x
(1 − sin x)2
− sin x + sin2 x + cos2 x
(1 − sin x)2
1
1 − sin x
=
=
2
(1 − sin x)
1 − sin x
=
elde edilir.
(sin2 x + cos2 x = 1)
112
Örnek 4.3.4. İki farklı metot kullanarak f (t) = sin t cos t fonksiyonunun türevini hesaplayınız.
Çözüm. Çarpım kuralını kullanarak
f ′ (t) = cos t cos t + sin t(− sin t) = cos2 t − sin2 t
elde edilir. Bir diğer çözüm yöntemi sin(2t) = 2 sin t cos t eşitliği kullanılarak
verilebilir. Buna göre
d 1
1
′
f (t) =
sin(2t) = (2) cos(2t) = cos(2t) = cos2 t − sin2 t
dt 2
2
sonucuna ulaşılır.
Diğer trigonometrik fonksiyonların türevleri ise
sin x
cos x
cos x
cot x =
sin x
eşitlikleri kullanıılarak elde edilir.
tan x =
1
cos x
1
csc x =
sin x
sec x =
Örnek 4.3.5. Tanjant ve sekant fonksiyonlarının türevlerini hesaplayınız.
Çözüm. Yukarıda tanjat ve sekant fonksiyonları için verilen ifadeleri kullanarak
(cos x)(cos x) − sin x(− sin x)
d sin x
d
=
tan x =
dx
dx cos x
cos2 x
=
ve
cos2 x + sin2 x
1
=
= sec2 x
2
cos x
cos2 x
d
−1
(cos x)
dx
sin x
1 sin x
= (−1)(cos x)−2 (− sin x) =
=
= sec x tan x
cos2 x
cos x cos x
d
d
sec x =
dx
dx
1
cos x
=
elde edilir.
Örnek 4.3.5’deki şekilde hareket ederek
d
d
cot x = − csc2 x
csc = − csc x cot x
dx
dx
olduğunun gösterilmesi okuyucuya alıştırma olarak bırakılmıştır.
Örnek 4.3.6.
x i 1
x i
h
x
1
d h
3x + cot
= 3 + − csc2
= 3 − csc2
dx
2
2
2
2
2
d
d
3
=
(3 csc(2x)) = 3(− csc(2x) cot(2x))(2) = −6 csc(2x) cot(2x)
dx sin(2x)
dx
113
Kapalı Fonksiyonların Türevleri
Bu kısımda Zincir Kuralı’nın özel bir durumu olan kapalı türev kavramı incelenecektir. Şimdiye kadar
y = 3x2 − sin(7x + 5)
gibi y = f (x) formunda “açık” bir şekilde x’e bağlı olarak yazılabilien y fonksiyonlarının türevleri incelendi ve türevlerinin Zincir Kuralı kullanılarak
y ′ = 6x − 7 cos(7x + 5)
şeklinde hesaplanabileceği gösterildi. Diğer taraftan kimi zaman
x3 + y 3 − 9xy = 0, y 2 − x = 0 ve x2 − y 2 − 25 = 0
gibi eşitlikler ile çalışmamız gerekebilir. Bu denklemler x ile y değişkenleri arasında “kapalı” bir ilişki tanımlar. Bazı durumlarda böyle bir denklemi, y’yi x’in
bir kapalı fonksiyonu şeklinde yazarak çözebiliriz. Bildiğimiz yoldan türev alırken F (x, y) = 0 denklemini y = f (x) şeklinde yazamasak da dy/dx türevini
gene de kapalı türev yolu ile bulabiliriz. Bu olgu aşağıdaki örnekte anlatılmaktadır.
Örnek 4.3.7. x2 + y 2 = 25 eğrisine (3, −4) noktasından çizilen teğetin eğimini
tespit ediniz.
Çözüm. x2 + y 2 = 52 denklemi merkezi (0, 0), yarıçapı 5 olan çemberi gösterir.
İstenen teğetin eğimi iki farklı şekilde bulunabilir.
√
Yöntem 1. x2 + y 2 = 25 denklemi sadece x’e bağlı olarak y1,2 = ± 25 − x2
√
şeklinde yazılabilir. Dikkat edilirse (3, −4) noktası y = − 25 − x2 eğrisinin
üzerindedir. Dolayısyla Zincir Kuralı kullanılarak
y′ =
p
dy
d
x
−2x
=
(− 25 − x2 ) = − √
=√
dx
dx
2 25 − x2
25 − x2
türev değeri elde edilir. Buna göre teğitin eğimi
x
dy 3
3
√
=√
=
2
2
dx x=3 25 − x
4
25 − 3
şeklinde bulunur.
Yöntem 2. Şimdi verilen denklemin y’yi kapalı olarak x’in türevlenebilir bir
fonksiyonu gibi tanımladığını varsayalım: y = y(x). Buna göre verilen kapalı
çember denkleminin her iki tarafından x’e göre türev alınırsa
d 2
d 2
d
dy
dy
x
(x ) +
(y ) =
25 ⇒ 2x + 2y
=0⇒
=−
dx
dx
dx
dx
dx
y
114
elde edilir. Buna göre teğerin eğimi
x 3
dy =− =
dx (3,−4)
y (3,−4)
4
olarak bulunur. Bu şekilde türev değerini hesaplama metoduna kapalı türev adı
verilir.
Örnek 4.3.8.
i) cos2 x + cos2 y = cos(2x + 2y) ise dy/dx türevini bulunuz.
ii) x2 y + y 4 = 4 + 2x ise d2 y/dx2 türevini bulunuz.
Çözüm. i) y’yi x’in fonksiyonu gibi düşünüp, y = y(x), denklemin kapalı olarak
türevini alırsak
d
d
d
(cos2 x) +
(cos2 y) =
(cos(2x + 2y))
dx
dx
dx
d
d
d
cos y = − sin(2x + 2y) (2x + 2y)
2 cos x cos x + 2 cos y
dx
dx
dx
dy
dy
2 cos x(− sin x) + 2 cos y(− sin y)
= − sin(2x + 2y) 2 + 2
dx
dx
dy
dy
−2 cos x sin x − 2 cos y sin y = −2 sin(2x + 2y) − 2 sin(2x + 2y)
dx
dx
dy
dy
2 sin(2x + 2y) − 2 cos y sin y = −2 cos x sin x + 2 sin(2x + 2y)
dx
dx
elde edilir. Buna göre türev
y′ =
cos x sin x − sin(2x + 2y)
dy
=
dx
sin(2x + 2y) − cos y sin y
olarak bulunur.
ii) Benzer şekilde y = y(x) olarak düşünüp denklemin kapalı olarak birinci
türevini alırsak
d 2
d
dy
dy
(x y + y 4 ) =
(4 + 2x) ⇒ 2xy + x2
+ 4y 3
=2
dx
dx
dx
dx
2 − 2xy
dy
= 2
y′ =
dx
x + 4y 3
elde edilir. Birinci türev ifadesinden tekrar türev alınarak
d
d
2
3
2
3
d2
2 − 2xy
dx (2 − 2xy)(x + 4y ) − dx (x + 4y )(2 − 2xy)
=
dx2 x2 + 4y 3
(x2 + 4y 3 )2
dy
dy
(x2 + 4y 3 ) − 2x + 12y 2 dx
(2 − 2xy)
−2 y + x dx
=
(x2 + 4y 3 )2
115
bulunur.
dy
dx
=
2−2xy
x2 +4y 3
olduğu kullanılarak
2 − 2xy
d2
y = 2
dx
x2 + 4y 3
(x2 + 4y 3 ) − 2x + 12y 2 x2−2xy
(2 − 2xy)
−2 y + x x2−2xy
2 +4y 3
2 +4y 3
=
(x2 + 4y 3 )2
′′
sonucuna ulaşılır.
Ters Trigonometrik Fonksiyonların Türevleri
Örnek 4.3.9.
d
dx
arcsin x =
√ 1
1−x2
olduğunu ispatlayınız.
dy
1
= √1−x
eşitliğinin sağlanKanıt. y = arcsin x olsun. Gösterilmesi gereken dx
2
dığıdır. Arcsinüs fonksiyonunun tanımı gereği biliyoruz ki
x = sin y ve −
π
π
≤y≤
2
2
ifadeleri geçerlidir. Yukarıdaki ilk ifadenin x’e göre türevi alınırsa
1=
d
d
dy
dy
d
(x) =
(sin y) =
(sin y)
= (cos y)
dx
dx
dy
dx
dx
olduğundan
1
dy
=
dx
cos y
2
2
2
2
elde edilir. Diğer taraftan
p sin y + cos y = 1 dolayısıyla cos y = 1 − sin y
olduğundan cos y = ± p1 − sin2 y elde edilir. Burada − π2 ≤ y ≤ π2 için cos y >
0 olduğundan cos y = 1 − sin2 y gerçeklenir. Buna göre
dy
1
1
=p
=√
2
dx
1 − x2
1 − sin y
bulunur.
Örnek 4.3.10.
d
dx
arccos x =
√ −1
1−x2
olduğunu ispatlayınız.
dy
−1
= √1−x
Kanıt. y = arccos x olsun. Gösterilmesi gereken dx
eşitliğinin sağlan2
dığıdır. Arckosinüs fonksiyonunun tanımı gereği biliyoruz ki
x = cos y ve 0 ≤ y ≤ π
ifadeleri geçerlidir. Yukarıdaki ilk ifadenin x’e göre türevi alınırsa
1=
d
d
dy
dy
d
(x) =
(cos y) =
(cos y)
= (− sin y)
dx
dx
dy
dx
dx
116
olduğundan
dy
−1
=
dx
sin y
elde edilir. Diğer taraftan sin2 y + cos2 y = 1 dolayısıyla sin2 y = 1 − cos2 y
p
olduğundan sin y = ± 1 − cos2 y elde edilir. Burada 0 ≤ y ≤ π için sin y > 0
p
olduğundan sin y = 1 − cos2 y gerçeklenir. Buna göre
dy
−1
−1
=p
=√
2
dx
1 − x2
1 − cos y
bulunur.
Örnek 4.3.11.
d
dx
arctan x =
1
1+x2
olduğunu ispatlayınız.
dy
1
Kanıt. y = arctan x olsun. Gösterilmesi gereken dx
= 1+x
2 eşitliğinin sağlandığıdır. Arctanjant fonksiyonunun tanımı gereği biliyoruz ki
x = tan y ve −
π
π
≤y≤
2
2
ifadeleri geçerlidir. Yukarıdaki ilk ifadenin x’e göre türevi alınırsa
1=
d
d
d
dy
dy
(x) =
(tan y) =
(tan y)
= (sec2 y)
dx
dx
dy
dx
dx
olduğundan
1
dy
=
dx
sec2 y
elde edilir. Diğer taraftan sin2 y + cos2 y = 1 dolayısıyla
olduğundan sec2 y = 1 + tan2 y elde edilir. Buna göre
sin2 y
cos2 y
+
cos2 y
cos2 y
=
1
cos2 y
dy
1
1
=
=
dx
1 + x2
1 + tan2 y
bulunur.
Logaritmik ve Üstel Fonksiyonların Türevleri
Logaritma fonksiyonunun türevi
lim (1 + n)
n→0
1/n
=e
eşitliğine dayanır. Burada e sayısı doğal logaritmanın tabanı olan e = 2.718281828459 · · ·
sayısıdır.
Örnek 4.3.12.
d
dx
ln x =
1
x
olduğunu ispatlayınız.
117
Kanıt. f (x) = ln x fonksiyonu x > 0 için tanımlıdır. Türev tanımı kullanılarak
f (x + h) − f (x)
1
x+h
ln(x + h) − ln x
f (x) = lim
= lim
= lim
ln
h→0
h→0
h→0 h
h
h
x
#
"
h1
1
h
h
(h/x = n olsun)
= lim
= lim ln 1 +
ln 1 +
h→0 h
h→0
x
x
h
i
x1 1
1
= lim ln (1 + n) nx = lim ln (1 + n) n
n→0
n→0
1
1
1
1
ln (1 + n) n = lim ln (1 + n) n
= lim
n→0 x
x n→0
1
1
= ln e =
x
x
′
elde edilir.
Örnek 4.3.13. x > 0, a > 0 ve a 6= 1 olmak üzere
ispatlayınız.
Kanıt.
d
dx
ln x =
1
x
d
dx (loga
x) =
1
x ln a
olduğunu
olduğu kullanılarak
f ′ (x) =
d
d
(loga x) =
dx
dx
ln x
ln a
=
1/x
1
=
ln a
x ln a
elde edilir.
Açıklama 4.3.14. En genel halde u = u(x) olmak üzere
d
1
d
1 ′
(loga u(x)) =
u′ (x) ve
(ln u(x)) =
u (x)
dx
u(x) ln a
dx
u(x)
sağlanır.
Örnek 4.3.15.
i) y = ln(sin x) ise dy/dx’i bulunuz.
ii) y = log10 (2 + sin x) ise dy/dx’i bulunuz.
iii) y = x
√
x
ise dy/dx’i bulunuz.
Çözüm. i) u = sin x olsun. Buna göre zincir kuralını kullanarak y = ln u fonksiyonunun türevi
dy du
1
1
dy
=
= cos u =
cos x = cot x
dx
du dx
u
sin x
118
olarak elde edilir.
ii) u = 2 + sin x olsun. Buna göre zincir kuralını kullanarak y = log10 u fonksiyonunun türevi
dy du
1
1
cos x
dy
=
=
cos x =
cos x =
dx
du dx
u ln 10
(2 + sin x)(ln 10)
(2 + sin x)(ln 10)
şeklinde bulunur.
√
iii) y = x x ifadesinden
y=x
√
x
⇒ y = xx
1/2
⇒ ln y = ln xx
1/2
⇒ ln y = x1/2 ln x
yazılır ve her iki tarafın x’e göre kapalı türevi alınırsa
1
ln x
1
1
1 ′
y = x−1/2 ln x + x1/2 = √ + √ ⇒
y
2
x
2 x
x
1
ln
x
√ +√
y′ = y
2 x
x
√
1
ln
x
√ +√
y′ = y = x x
2 x
x
sonucuna ulaşılır.
Örnek 4.3.16.
d x
dx e
= ex olduğunu ispatlayınız.
Kanıt. y = ex olsun. Buna göre x = ln y elde edilir. Son eşitliğin her iki tarafından y’ye göre türev alırsak
d
1
dy
d x
dx
=
(ln y) = ⇒
= y sonuçta
e = ex
dy
dy
y
dx
dx
elde edilir.
Örnek 4.3.17.
d
x
dx (a )
= ax ln a olduğunu ispatlayınız.
Kanıt. y = ax olsun. Buna göre ln y = ln ax yani ln y = x ln a sağlanır. Bu
ifadenin her iki yanından x’e göre türev alırsak
d
d
1 dy
dy
(ln y) =
(x ln a) ⇒
= ln a ⇒
= y ln a
dx
dx
y dx
dx
sonuçta
dy
= ax ln a
dx
elde edilir.
119
Açıklama 4.3.18. En genel halde u = u(x) olmak üzere
d u(x)
d u(x)
(a
) = au(x) ln a · u′ (x) ve
(e
) = eu(x) u′ (x)
dx
dx
sağlanır.
Örnek 4.3.19.
ii) y = xe
√
1−x
i) y = 2sin 3x ise dy/dx’i bulunuz.
ise dy/dx’i bulunuz.
Çözüm. i) u = sin 3x olsun. Buna göre y = 2u fonksiyonunun türevi
dy
dy du
d u d
=
=
(2 ) (sin 3x) = 2u ln 2 · 3 cos 3x
dx
du dx
du
dx
yani
dy
= 3 · 2sin 3x ln 2 · cos 3x
dx
elde edilir.
ii) Gerekli işlemler yapılarak
√
√
√
√
xe 1−x
−1
dy
= 1e 1−x + xe 1−x √
= e 1−x − √
dx
2 1−x
2 1−x
sonucuna ulaşılır.
4.4
Ortalama Değer Teoremi
Ortalama Değer Teoremi, bir fonksiyonunu türevi ile bu fonksiyona ait kirişlerin
bir tanesinin eğimi arasındaki ilişkiyi ortaya koyar. Şimdi özel bir durumu içeren
aşağıdaki sonucu verelim.
Lemma 4.4.1 (Rolle Teoremi). a < b olmak üzere a, b ∈ R reel sayıları göz
önüne alınsın. Eğer f fonksiyonu [a, b] aralığında sürekli, (a, b) aralığında diferansiyellenebilir ve f (a) = f (b) ise f ′ (c) = 0 olacak şekilde bir c ∈ (a, b) sayısı
vardır.
Kanıt. Ekstremum Değer Teoremi (Teorem 3.3.8) gereği f fonksiyonunun [a, b]
kapalı aralığında sonlu bir M maksimum ve m minimum değeri vardır. Eğer
M = m ise f fonksiyonu (a, b) üzerinde sabit sabit fonksiyon olmak zorundadır
ve bu durumda her x ∈ (a, b) için f ′ (x) = 0 sağlanır.
M 6= m olsun. f (a) = f (b) eşitliği gerçeklendiğinden bir c ∈ (a, b) noktasının fonksiyon altındaki değeri M veya m’e eşit olacak şekilde seçilebilir.
120
Genelliği bozmadan f (c) = M olsun (eğer f (c) = m ise benzer tarzda hareket ederek istenilen gösterilebilir). M noktası [a, b] aralığında f fonksiyonunun
maksimumu olduğundan c + h ∈ (a, b) koşulunu sağlayan tüm h değerleri için
f (c + h) − f (c) ≤ 0
eşitsizliği gerçeklenir. Eğer h > 0 ise
f ′ (c) = lim
f (c + h) − f (c)
≤0
h
f ′ (c) = lim
f (c + h) − f (c)
≥0
h
h→0+
ve h > 0 ise
h→0−
olduğundan f ′ (c) = 0 eşitsizliğinin doğruluğu elde edilir.
Açıklama 4.4.2. Rolle Teoremi’ndeki süreklilik hipotezi [a, b] aralığındaki bir
nokta için bile sağlanmasa teorem doğruluğunu yitirir.
Kanıt. Aşağıdaki
f (x) =

x
0
x ∈ [0, 1)
x=1
fonksiyonu göz önüne alınsın. Bu fonksiyon açıkça [0, 1) aralığında sürekli, (0, 1)
üzerinde diferansiyellenebilir ve f (0) = f (1) = 0 olduğu halde f ′ (x) değeri hiç
bir zaman sıfıra eşit değildir.
Açıklama 4.4.3. Rolle Teoremi’ndeki diferansiyellenebilirlik hipotezi (a, b)
aralığındaki bir nokta için bile sağlanmasa teorem doğruluğunu yitirir.
Kanıt. Biliyoruz ki f (x) = |x| fonksiyonu [−1, 1] aralığında sürekli, (−1, 1)\{0}
üzerinde diferansiyellenebilir ve f (−1) = f (1) = 1 olduğu halde f ′ (x) değeri
hiç bir zaman sıfıra eşit değildir.
Teorem 4.4.4. a < b olmak üzere a, b ∈ R reel sayıları göz önüne alınsın.
i) [Genelleştirilmiş Ortalama Değer Teoremi] Eğer f ve g fonksiyonları [a, b]
aralığında sürekli ve (a, b) aralığında diferansiyellenebilir ise
g ′ (c)(f (b) − f (a)) = f ′ (c)(g(b) − g(a))
eşitliğini sağlayacak şekilde bir c ∈ (a, b) sayısı vardır.
121
ii) [Ortalama Değer Teoremi] Eğer f fonksiyonu [a, b] aralığında sürekli ve
(a, b) aralığında diferansiyellenebilir ise
f (b) − f (a) = f ′ (c)(b − a)
eşitliğini sağlayacak şekilde bir c ∈ (a, b) sayısı vardır.
Kanıt. i)
h(x) = f (x)(g(b) − g(a)) − g(x)(f (b) − f (a))
olsun. Bu fonksiyonun
h′ (x) = f ′ (x)(g(b) − g(a)) − g ′ (x)(f (b) − f (a))
türev fonksiyonu açıkça [a, b] üzerinde sürekli ve (a, b) üzerinde diferansiyellenebilirdir. Ayrıca
h(a) = f (a)(g(b) − g(a)) − g(a)(f (b) − f (a))
ve
= f (a)g(b) − f (a)g(a) − g(a)f (b) + g(a)f (a) = f (a)g(b) − g(a)f (b)
h(b) = f (b)(g(b) − g(a)) − g(b)(f (b) − f (a))
= f (b)g(b) − f (b)g(a) − g(b)f (b) + g(b)f (a) = g(b)f (a) − f (b)g(a)
sağlandığından h(a) = h(b) eşitliği gerçeklenir. Dolayısıyla Rolle Teoremi’ne
göre h′ (c) = 0 olacak şekilde bir c ∈ (a, b) sayısı vardır.
ii) Eğer i) şıkkında g(x) = x alınır ise istenilen gösterilmiş olur.
Rolle Teoremi c ∈ (a, b) için eğriye (c, f (c)) noktasından çizilen teğetin
x-eksenine paralel olduğunu söyler. Bununla beraber Ortalama Değer Teoremi
benzer koşullarda bir c ∈ (a, b) için (c, f (c)) noktasından çizilen teğetin (a, f (a))
ve (b, f (b)) noktalarını birleştiren kirişe paralel olacağını belirtir. Genelleştirilmiş Ortalam Değer Teoremi aynı zamanda Cauchy Ortalama Değer Teoremi
olarak da bilinir.
Teğet
y
y
Kiriş
f (b)
y = f (x)
a
c
b
y = f (x)
f (a)
x
a
122
c
b
x
Tanım 4.4.5. R reel sayıların bir alt kümesi E göz önüne alınsın ve f : E → R
olsun.
i) f fonksiyonunun E üzerinde artan (sırası ile kesinlikle artan) olarak isimlendirilmesi için gerek ve yeter şart x1 < x2 koşulunu sağlayan x1 , x2 ∈ E
için f (x1 ) ≤ f (x2 ) (sırası ile f (x1 ) < f (x2 )) eşitsizliğinin sağlanmasıdır.
ii) f fonksiyonunun E üzerinde azalan (sırası ile kesinlikle azalan) olarak
isimlendirilmesi için gerek ve yeter şart x1 < x2 koşulunu sağlayan x1 , x2 ∈
E için f (x1 ) ≥ f (x2 ) (sırası ile f (x1 ) > f (x2 )) eşitsizliğinin sağlanmasıdır.
iii) f fonksiyonunun E üzerinde monoton (sırası ile kesinlikle monoton) olarak isimlendirilmesi için gerek ve yeter şart ya artan ya da azalan (sırası
ile ya kesinlikle artan ya da kesinlikle azalan) olmasıdır.
Dikkat edilirse f (x) = x2 fonksiyonu [0, 1] ve [−1, 0] üzerinde kesinlikle
monotonken [−1, 1] aralığında monoton değildir.
Teorem 4.4.6. a 0 (sırası ile f ′ (x) < 0) ise f fonksiyonu
[a, b] üzerinde kesinlikle artandır (sırası ile kesinlikle azalandır).
ii) Eğer her x ∈ (a, b) için f ′ (x) = 0 ise f fonksiyonu [a, b] üzerinde sabittir.
iii) Eğer g fonksiyonu [a, b] üzerinde sürekli, (a, b) aralığında diferansiyellenebilir ve her x ∈ (a, b) için f ′ (x) = g ′ (x) sağlanıyor ise [a, b] üzerinde
f − g fonksiyonu sabittir.
Kanıt. i) a ≤ x1 < x2 ≤ b olsun. Ortalama Değer Teoremi’ne göre f (x2 ) −
f (x1 ) = f ′ (c)(x2 − x1 ) eşitliğini sağlayacak şekilde bir c ∈ (a, b) sayısı vardır.
Buna göre eğer f ′ (c) > 0 ise f (x2 ) > f (x1 ) ve eğer f ′ (c) < 0 ise f (x2 ) < f (x1 )
gerçeklenir. Dolayısıyla istenilen gösterilmiş olur.
ii) Eğer f ′ = 0 ise i) şıkkının istapına göre f fonksiyonu hem artan hem de
azalandır. Dolayısıyla [a, b] üzerinde sabit olmak zorundadır.
iii) Yıkarıda verilen ii) şıkkının ispatı f −g için uygulanırsa istenilen gösterilmiş
olur.
Teorem 4.4.6 i) şıkkı diferansiyellenebilir fonksiyonların monotonluğu hakkında yorum yapma imkanı sağlar. Bununla birlikte monoton olduğu halde
diferansiyellenebilir olmayan fonksiyonlar da vardır. Örneğin
f (x) = ⌊x⌋ := n, n ≤ x < n + 1, n ∈ Z
123
en büyük tamsayı fonksiyonu R üzerinde artan olmakla birlikte ne sürekli ne
de diferansiyellenebilir değildir.
Peki bu diferansiyellenemeyen monoton fonksiyonların davranışları ne şekildedir. Aşağıdaki sonuç tıpkı en büyük tamsayı fonksiyonunda olduğu gibi bir
aralıkta monoton olan herhangi bir fonksiyonun daima sağdan ve soldan limitlerinin var olduğunu ortaya koyar. Bu sonuç Monoton Yakınsaklık Teoremi’nin
(Teorem 2.3.2) fonksiyonlar için analoğudur.
Teorem 4.4.7. f fonksiyonu [a, b] aralığında artan olsun.
i) Eğer c ∈ [a, b) ise f (c+) limiti mevcuttur ve f (c) ≤ f (c+) eşitsizliği
sağlanır.
ii) Eğer c ∈ (a, b] ise f (c−) limiti mevcuttur ve f (c−) ≤ f (c) eşitsizliği
sağlanır.
Kanıt. Simetriden ötürü verilen bir c ∈ (a, b] için f (c−) limitinin var ve f (c−) ≤
f (c) olduğunu göstermek yeter. E = f ((a, c)) ve s = sup E olsun. f fonksiyonu
artan olduğundan f (c) değeri E’nin bir üst sınırıdır. Buna göre s bir sonlu sayı
olarak s ≤ f (c) eşitsizliğini gerçekler. Supremum için Yaklaşım Özelliği’nden
(Teorem 1.3.5) s − ε < f (x0 ) ≤ s olacak şekilde bir x0 ∈ (a, c) sayısı vardır. f
fonksiyonunun artan olduğu göz önüne alındığında her x0 < x < c için
s − ε < f (x0 ) ≤ f (x) ≤ s
eşitsizliği gerçeklenir. Buna göre f (c−) limiti vardır ve f (c−) = s ≤ f (c)
eşitsizliği gerçeklenir.
124
Örnek 3.3.14’den biliyoruz ki hiç bir yerde sürekli yani sayılamayan sonsuz
noktada süreksizliği olan fonksiyonlar mevcuttur. Peki bir monoton fonksiyon
kaç tane süreksizlik noktasına sahip olabilir?
Teorem 4.4.8. Eğer f fonksiyonu bir I aralığında monoton ise I üzerinde f
fonksiyonunun en fazla sayılabilir sayıda süreksizlik noktası olabilir.
Örnek 4.4.9. Her x > 0 için 1 + x < ex olduğunu ispatlayınız.
Kanıt. f (x) = ex − x olsun. Her x > 0 için f ′ (x) = ex − 1 > 0 olduğundan Teorem 4.4.6 i) şıkkına göre f (x) fonksiyonu (0, ∞) aralığında kesinlikle artandır.
Dolayısıyla her x > 0 için ex − x = f (x) > f (0) = 1 gerçeklenir. Yani, x > 0
için ex > x + 1 gerçeklenir.
Teorem 4.4.10 (Türevler için Ara Değer Teoremi). f fonksiyonu f ′ (a) 6= f ′ (b)
olmak üzere [a, b] aralığında diferansiyellenebilir olsun. Eğer y0 sayısı f ′ (a)
ile f ′ (b) arasında yer alıyor ise f ′ (x0 ) = y0 eşitliğini sağalayacak şekilde bir
x0 ∈ (a, b) sayısı vardır.
Strateji: F (x) := f (x) − y0 x olsun. Buna göre F ′ (x0 ) := f ′ (x0 ) − y0 = 0
eşitliğini sağlayacak şekilde bir x0 ∈ (a, b) sayısı bulmamız gerekir. Diferansiyellenebilir bir F fonksiyonunun lokal ekstremumları F ′ türevinin sıfıra eşit
olduğu yerlerde bulunduğundan F fonksiyonunun bir x0 ∈ (a, b) noktasında
lokal ekstremumu olduğunu göstermek yeter.
Kanıt. y0 değeri f ′ (a) ile f ′ (b) arasında yer alsın. Simetriden ötürü f ′ (a) <
y0 < f ′ (b) olduğunu farz edebiliriz. Her x ∈ (a, b) için F (x) = f (x) − y0 x
olarak tanımlansın. Buna göre F fonksiyonu [a, b] aralığında diferansiyellenebilirdir. Dolayısıyla, Ekstremum Değer Teoremi’ne (Teorem 3.3.8) göre [a, b]
üzerinde F fonksiyonunun bir mutlak maksimum, F (x0 ) değeri vardır. Diğer
taraftan F ′ (a) = f ′ (a)−y0 < 0 olduğundan F fonksiyonu azalandır. Dolayısıyla
yeterince küçük h > 0 için F (a + h) − F (a) < 0 yani F (a + h) < F (a) sağlanır. Bu ise bize F (a)’nın [a, b] üzerinde F fonksiyonunun mutlak minimumu
olmadığını gösterir. Dolayısıyla mutlak minimum F (x0 ) değeri mutlaka (a, b)
üzerinde olmalıdır. Yani F ′ (x0 ) = 0 olacak şekilde bir x0 ∈ (a, b) sayısı vardır.
Bu ise isteneni ispatlar.
4.5
Limitlerde Belirsiz Şekiller ve L’Hôpital Kuralı
Aşağıdaki sonuç 0/0 ve ∞/∞ formundaki limitleri hesaplamada sıkça kullanılır.
125
Teorem 4.5.1 (L’Hôpital Kuralı). a bir genişletilmiş reel sayı, a’nın bir iç
veya uç noktası olduğu bir açık aralık I, f ve g fonksiyonları I\{a} üzerinde
diferansiyellenebilir ve her x ∈ I\{a} için g(x) 6= 0 6= g ′ (x) olsun. Ayrıca,
A := x→a
lim f (x) = x→a
lim g(x)
x∈I
x∈I
değeri ya 0 ya da ∞ olsun. Eğer
B := x→a
lim
x∈I
f ′ (x)
g ′ (x)
limiti bir genişletilmiş reel sayı olarak var ise
lim
x→a
x∈I
f ′ (x)
f (x)
= x→a
lim ′
g(x)
g (x)
x∈I
sağlanır.
(x)
limx→a fg(x)
limitini l’Hôpital kuralı ile bulmak için x → a iken 0/0 veya
x∈I
∞/∞ formunu elde ettiğimiz sürece f ve g ifadelerinin türevlerini almaya devam ederiz.
0\0 Belirsizliği
Örnek 4.5.2. Aşağıdaki limitleri hesaplayınız.
√
1+x−1
(a) limx→0
x
(b) limx→∞
sin x1
arctan x1
(c) limx→0
sin x2 − ln(1 + x2 )
1 − cos x2
(d) limx→0
x3 cos x1
1 − sec x
(e) limx→0−
sin x
x2
Çözüm. Bu tip belirsizliklerde doğrudan l’Hôpital Kuralı uygulanır.
√
√1
1 + x − 1 00
2 1+x
(a) limx→0
= limx→0
= 21
x
1
0
sin x1
− x12 cos x1 00
1
1
0
1+ 2 =1
(b) limx→∞
= limx→∞
= limx→∞ cos
− x12
x
x
arctan x1
1+ x12
126
(c)
2x
1
2x cos x2 − 1+x
cos x2 − 1+x
sin x2 − ln(1 + x2 ) 00
2
2
=
lim
=
lim
x→0
x→0
x→0
1 − cos x2
2x sin x2
sin x2
2x
0
−2x sin x2 + (1+x
2 )2
0
= lim
x→0
2x cos x2
1
− sin x2 + (1+x
2 )2
= lim
=1
x→0
cos x2
lim
(d) Her a ∈ R için −1 ≤ cos a ≤ 1 sağlandığından limx→0 cos x1 limit değeri
sonludur. limx→0 cos x1 = k olsun. Buna göre
x3 cos x1
x3
1
x3
lim cos
= k lim
= lim
lim
x→0
x→0 1 − sec x
x→0 1 − sec x
x→0 1 − sec x
x
2
0
x 3x
0
(x cos2 x)
= −3k lim
=
k lim
x→0 sin x
x→0 − sec x tan x
= −3k · 1 · 0 = 0
(e) limx→0−
sin x 00
cos x
=
= limx→0−
x2
2x
1
0−
= −∞
∞\∞, ∞ · 0, ∞ − ∞ Belirsizlikleri
∞\∞ formundaki belirsizliklerde doğrudan l’Hôpital Kuralı uygulanır.
Örnek 4.5.3. Aşağıdaki limitleri hesaplayınız.
(a) limx→ π4
tan 2x
ln(4x − π)
(b) limx→∞
x(ln x)2
e2x
Çözüm. (a)
limπ
x→ 4
tan 2x ∞
2 sec2 2x
4x − π
∞
= limπ
=
limπ
4
x→ 4 2 cos2 2x
x→ 4
ln(4x − π)
4x−π
0
0
=
limπ
x→ 4
4
4
= =∞
−8 cos 2x sin 2x
0
(b)
∞
(ln x)2 + 2x(ln x) x1
(ln x)2 + 2(ln x)
x(ln x)2 ∞
=
lim
=
lim
x→∞
x→∞
x→∞
e2x
2e2x
2e2x
1
1
∞
2(ln x) x + 2 x
(ln x) + 1
∞
= lim
=
lim
x→∞
x→∞
4e2x
2xe2x
1
∞
0
∞
x
=
lim
=
=0
x→∞ 2e2x + 4xe2x
∞
lim
127
∞ · 0 ve ∞ − ∞ tipindeki belirsizlikler cebirsel işlemler ile 0\0 veya ∞\∞
formuna çevrilerek l’Hôpital kuralı uygulanarak limit bulunur.
Örnek 4.5.4. Aşağıdaki limitleri hesaplayınız.
x
xπ
(a) limx→2 ln
tan
2
4
x
π −
(b) limx→ π2
cot x 2 cos x
Çözüm. (a)
1
ln x2 00
x
xπ 0·∞
x
lim ln
tan
= lim
= lim π
2
x→2
x→2 cot xπ
x→2 −
2
4
4
4 1 + cot
xπ
4
(b)
limπ
x→ 2
=
1
2
− π4
=−
2
π
x
2x cos x − π cot x
π ∞−∞
= limπ
−
x→ 2
cot x 2 cos x
2 cos x cot x
2x sin x − π 00
2 sin x + 2x cos x
2
= limπ
= limπ
=
= −1
x→ 2
x→ 2
2 cos x
−2 sin x
−2
Belirsiz Kuvvetler
1∞ , 00 ve ∞0 formundaki belirsizlikler de fonksiyonun logaritması alınarak
daha önceden çözümü bilinen hallerden birisine dönüştürülebilir. Buna göre,
eğer a genişletilmiş reel sayısı için limx→a ln f (x) = L ise
lim f (x) = lim eln f (x) = eL
x→a
x→a
elde edilir.
Örnek 4.5.5. limx→0+ (1 + x)1/x = e olduğunu gösteriniz.
Çözüm. Verilen limt 1∞ formunda bir belirsizliğe sahiptir. f (x) = (1 + x)1/x
olsun ve limx→0+ ln f (x) limit değerini hesaplayalım. Buna göre
ln f (x) = ln(1 + x)1/x =
1
ln(1 + x)
x
olduğundan
1
1
ln(1 + x) 00
1
∞·0
ln(1 + x) = lim
= lim 1+x = = 1
x→0+ x
x→0+
x→0+ 1
x
1
lim ln f (x) = lim
x→0+
128
elde edilir. Yani,
lim ln f (x) = 1
x→0+
olduğundan
lim (1 + x)1/x = lim f (x) = lim eln f (x) = e1 = e
x→0+
x→0+
x→0+
sonucuna ulaşılır.
Örnek 4.5.6. limx→0 (cot x)sin x limitini hesaplayınız.
Çözüm. Dikkat edilirse limit ∞0 belirsizliğine sahiptir. Eğer f (x) = (cot x)sin x
denir ise
ln f (x) = ln(cot x)sin x = sin x ln(cot x)
elde edilir. Buna göre
0·∞
lim ln f (x) = lim sin x ln(cot x) = lim
x→0
x→0
x→0
2
∞
ln(cot x)
− −1/cotsinx
cos x
x→0
− sin
2x
x
∞
=
lim
= lim
x→0
1
sin x
sin x
=0
cos2 x
olduğundan istenen limit değeri
lim (cot x)sin x = e0 = 1
x→0
şeklinde bulunur.
Örnek 4.5.7. limx→0 (x + sin x)tan x limitini hesaplayınız.
Çözüm. Verilen limit 00 formunda bir belirsizliğe sahiptir. Eğer f (x) = (x +
sin x)tan x denir ise
ln f (x) = ln(x + sin x)tan x = tan x ln(x + sin x) =
ln(x + sin x)
cot x
elde edilir. Buna göre
1+cos x
ln(x + sin x) ∞
∞
=
lim x+sin x
x→0
x→0 − 12
cot x
sin x
lim ln f (x) = lim tan x ln(x + sin x) = lim
x→0
x→0
(− sin x)(1 + cos x)
0
(− sin2 x)(1 + cos x)
= lim
=0
=
x
x→0
x→0
x + sin x
1+1
sin x + 1
= lim
olduğundan istenen limit değeri
lim (x + sin x)tan x = e0 = 1
x→0
şeklinde bulunur.
129
4.6
Fonksiyon Graﬁklerinin Çizimi
Limit, süreklilik ve türev gibi kavramlar kullanarak verilen bir fonksiyonun
graﬁği çizilebilir. Bunun için aşağıdaki tanımlara ihtiyaç vardır.
Tanım 4.6.1 (Düşey Asimptotlar). f : A → R bir fonksiyon ve a ∈ A olsun.
i) limx→a+ f (x) = ±∞ ise x = a doğrusuna f fonksiyonunun sağdan düşey
asimptotu denir.
ii) limx→a− f (x) = ±∞ ise x = a doğrusuna f fonksiyonunun soldan düşey
asimptotu denir.
iii) x = a doğrusu f fonksiyonunun hem sağdan hem de soldan düşey asimptotu ise x = a doğrusuna f ’nin düşey asimptotu denir.
1
Örnek 4.6.2. f (x) = 5−x
şeklinde tanımlı f : R\{5} → R fonksiyonunun eğer
varsa düşey asimptotlarını bulunuz.
Çözüm.
1
1
= −∞ ve lim f (x) = lim
=∞
x→5+ 5 − x
x→5−
x→5− 5 − x
lim f (x) = lim
x→5+
olduğundan x = 5 doğrusu f fonksiyonunun hem sağdan hem soldan düşey
asimptotudur. Bu durumda x = 5 doğrusu f ’in düşey asimptotudur
Tanım 4.6.3 (Yatay ve Eğik Asimptotlar). Bazı a ∈ R için (a, ∞) ⊆ A olmak
üzere f : A → R bir fonksiyon olsun.
lim (f (x) − (mx + c)) = 0 veya
x→∞
lim (f (x) − (mx + c)) = 0
x→−∞
olacak şekilde bir y = mx + c doğrusu varsa y = mx + c doğrusuna f fonksiyonunun bir eğik asimptotu denir. Burada m = 0 ise yani
lim f (x) = c veya lim f (x) = c
x→−∞
x→∞
ise y = c doğrusuna f ’in yatay asimptotu denir.
Önerme 4.6.4. f fonksiyonunun eğik ya da yatay asimptotu varsa tek türlü
belirlidir.
1
Örnek 4.6.5. f (x) = 1 + 5−x
şeklinde tanımlı f : R\{5} → R fonksiyonunun
eğer varsa düşey asimptotlarını bulunuz.
130
Çözüm.
lim f (x) = lim
x→∞
x→∞
1+
1
5−x
= 1 ve
lim f (x) = lim
x→−∞
x→−∞
1+
1
5−x
olduğundan y = 1 doğrusu f fonksiyonunun yatay asimptotudur
=1
Eğik Asimptotun Bulunması. Bir f fonksiyonunun eğer varsa eğik asimptotu varsa aşağıdaki şekilde bulunur.
i) limx→∞ f (x) = c olacak şekilde bir c ∈ R varsa y = c doğrusu f fonksiyonunun yatay asimptotudur.
ii) limx→∞ f (x) = ∞ veya limx→∞ f (x) = −∞ ise limx→∞ f (x)
limitinin
x
var olup olmadığına bakılır. Bu limit var ve sıfırdan farklı ise
lim
x→∞
f (x)
=m
x
denir. Bundan sonra limx→∞ (f (x) − mx) limitinin var olup olmadığına
bakılır. Bu limit varsa
lim (f (x) − mx) = c
x→∞
denir. Bu durumda y = mx + c doğrusu f fonksiyonunun eğik asimptotu
olur.
x2
şeklinde tanımlı f : R\{1} → R fonksiyonunun
3(x − 1)
eğik asimptotunu bulunuz.
Örnek 4.6.6. f (x) =
2
x
Çözüm. limx→∞ f (x) = limx→∞ 3(x−1)
= ∞ olduğundan f fonksiyonunun eğik
asimptotu olabilir. Diğer taraftan
f (x)
lim
= lim
x→∞ x
x→∞
x2
3(x−1)
x
x2
1
= =m
x→∞ 3(x2 − x)
3
= lim
elde edilir. Buna göre
lim (f (x) − mx) = lim
x→∞
x→∞
x2
x
−
3(x − 1)
3
sonucuna ulaşılır. Eğer c = 1/3 denir ise y =
eğik asimptotudur. Ayrıca
= lim
x+1
3
x→∞
x
1
=
3x − 3
3
doğrusu f fonksiyonunun
lim f (x) = ∞ ve lim f (x) = −∞
x→1+
x→1−
olduğundan x = 1 noktasında fonksiyonun düşey asimptotu vardır.
131
Fonksiyon Graﬁklerinin Çizimi. Bir f fonksiyonunun graﬁğini çizerken genellikle aşağıdaki yol izlenir.
i) Eğer verilmemişse fonksiyonun tanım kümesi bulunur.
ii) Fonksiyonun eksenleri kestiği noktalar (varsa) bulunur:
• 0, f ’in tanım kümesine aitse f (0) değeri bulunarak fonksiyonun graﬁğinin y-eksenini kestiği nokta bulunur.
• f (x) = 0 eşitliğini sağlayan x değerleri varsa (belirlenebiliyorsa) bulunarak fonksiyonun x-eksenini kestiği nokta veya noktalar bulunur.
iii) Fonksiyonun yerel maksimum ve yerel minimumları incelenir: f diferansiyellenebilir ise f ′ (x0 ) = 0 eşitliğini sağlayan f ’in ekstremum noktaları
(varsa) bulunur.
• Eğer f ′ türevinin işareti x0 ’ın solunda negatif sağında pozitifse x0
noktasında f ’in yerel minimumu vardır.
• Eğer f ′ türevinin işareti x0 ’ın solunda pozitif sağında negatifse x0
noktasında f ’in yerel maksimumu vardır.
Yerel maksimum ve yerel minimumlar ikinci türev testi ile de bulunabilir:
• Eğer f ′′ (x0 ) > 0 ise f ’in x0 noktasında yerel minimumu vardır.
• Eğer f ′′ (x0 ) < 0 ise f ’in x0 noktasında yerel maksimumu vardır.
• Eğer f ′′ (x0 ) = 0 ise bu test sonuç vermez. x0 noktasında bir ekstremum olabilir ya da olmayabilir.
iv) f ’in konkavitesi ve büküm noktaları incelenir: f ′′ türevi varsa ve bir aralık
üzerinde
• Eğer f ′′ (x) > 0 ise verilen aralıkta f fonksiyonu yukarı konkavdır.
• Eğer f ′′ (x) < 0 ise verilen aralıkta f fonksiyonu aşağı konkavdır.
• Eğer fonksiyonunun gösterdiği eğri üzerindeki bir noktada konkavlık yön değiştiriyorsa bu noktaya büküm noktası denir. Eğer c bir
büküm noktası ise ya f ′′ (x) = 0 eşitliği sağlanır ya da f ′′ (x) ikinci
türevi mevcut değildir.
v) Fonksiyonun tek veya çift olup olmadığına bakılır: f ’in tanım bölgesindeki
tüm x değerleri için
• f (−x) = −f (x) sağlanıyor ise f fonksiyonu tek fonksiyon,
• f (−x) = f (x) sağlanıyor ise f fonksiyonu çift fonksiyondur.
Buna göre:
• Fonksiyon çift ise x ≥ 0 için çizim yapılır, oluşan görüntünün yeksenine göre, simetriği alınarak graﬁk tamamlanır.
132
• Fonksiyon tek ise, x ≥ 0 için çizim yapılır, oluşan görüntünün orijine
göre simetriği alınarak graﬁk tamamlanır.
vi) Eğer fonksiyon periyodik ise, fonksiyonun periyodu bulunur. Esas periyotta çizim yapılır; diğer aralıklarda çizim tekrarlanır.
vii) Fonksiyonun monotonluğu incelenir. Bir aralık üzerinde diferansiyellenebilir f fonksiyonu için
• Eğer f ′ (x) > 0 ise f fonksiyonu bu aralık üzerinde artandır.
• Eğer f ′ (x) < 0 ise f fonksiyonu bu aralık üzerinde azalandır
viii) Fonksiyonun asimptotları bulunur.
ix) Fonksiyonun değişim tablosu yapılır ve bu değerlere göre graﬁk çizilir.
Graﬁklerin Basit Dönüşümleri. Verilen bir f fonksiyonu cinsinden yazılabilen bazı fonksiyonların graﬁkleri f ’in graﬁği yardımıyla çizilebilir. Böylece
graﬁk çizmedeki işlem yükünü azaltmış oluruz. Şimdi bazı özel durumları inceleyelim.
i) g(x) = f (x + a) şeklinde tanımlı g fonksiyonunun graﬁği f fonksiyonunun
graﬁğinin, x-ekseni boyunca, |a|’nın değeri kadar, a nın işaretinin tersi
yönünde kaydırılarak bulunur.
ii) g(x) = f (x) + b fonksiyonunun graﬁği, f fonksiyonunun graﬁğinin, yekseni boyunca, |b|’nin değeri kadar, b’nin işaretinin yönünde kaydırılarak
bulunur.
iii)
a) k > 1 olmak üzere g(x) = f (kx) fonksiyonunun graﬁği f fonksiyonunun graﬁğinin y-eksenine doğru yatay olarak k defa sıkıştırılmasıyla
elde edilir.
b) 0 < k < 1 olmak üzere g(x) = f (kx) fonksiyonunun graﬁği f fonksiyonunun graﬁğinin y-ekseninden yatay olarak 1/k defa açılarak elde
edilir.
iv)
a) k > 1 olmak üzere g(x) = kf (x) fonksiyonunun graﬁği f fonksiyonunun graﬁğinin x-ekseninden (dikey yönde) k kere açılarak elde
edilir.
b) 0 < k < 1 olmak üzere g(x) = kf (x) fonksiyonunun graﬁği f fonksiyonunun graﬁğinin x-eksenine doğru (yani dikey yönde) 1/k kere
sıkıştırılarak bulunur.
v)
a) g(x) = −f (x) fonksiyonunun graﬁği, f fonksiyonunun graﬁğinin,
x-eksenine göre simetriğidir.
b) g(x) = f (−x) fonksiyonunun graﬁği ise, f fonksiyonunun graﬁğinin
y-eksenine göre simetriğidir.
133
vi) g(x) = f (|x|) fonksiyonunun graﬁği x ≥ 0 için f ’in graﬁği aynen korunarak ve x ≤ 0 için f fonksiyonunun x ≥ 0 için çizilen graﬁğinin y-eksenine
göre simetriği alınarak bulunur.
vii) g(x) = |f (x)| fonksiyonunun graﬁği, f fonksiyonunun graﬁğinden kolayca
bulunabilir. f fonksiyonunun graﬁğinin x-ekseninin üzerinde kalan parçaları aynen muhafaza edilir ve sonra da f fonksiyonunun graﬁğinin xekseninin altında kalan parçalarının x-eksenine göre simetriği alınarak g
nin graﬁği elde edilir.
viii) y = λf (kx + a) + b şeklindeki daha karışık fonksiyonların graﬁği (i)-(v)
dönüşümleri ard arda uygulanarak çizilebilir.
4.7
Ters Fonksiyon Teoremleri
Bu bölümde ters fonksiyonların sürekliliği ve diferansiyellenebilmesi olguları
üzerinde durulacaktır.
Biliyoruz ki, f : X → Y fonksiyonunun bir f −1 tes fonksiyonuna sahip olabilmesi için gerek ve yeter şart f ’in 1-1 ve üzerine olmasınır (bkz Teorem 1.4.1).
Bu durumda her x ∈ X için f −1 (f (x)) = x ve her y ∈ Y için f (f −1 (y)) = y
eşitlikleri gerçeklenir. (x, f (x)) = (f −1 (y), y) olduğundan y = f −1 (x) ters fonksiyonunun graﬁği y = f (x) fonksiyonunun graﬁğinin y = x doğrusuna göre
simetriğidir. Dolayısıyla, f −1 eğrisi f eğrisi kadar düzgündür. Buna göre aşağıdaki iki sonucu verebiliriz.
y=x
. (y, x)
f ’in graﬁği
.
(x, y)
f −1 ’in graﬁği
Teorem 4.7.1. I dejenere olmayan bir aralık ve f : I → R fonksiyonu 11 olsun. Eğer f fonksiyonu I üzerinde sürekli ise J := f (I) bir aralıktır, f
fonksiyonu I üzerinde kesinlikle artandır ve f −1 ters fonksiyonu J üzerinde
sürekli ve kesinlikle monotondur.
134
f fonksiyonu (a, b) aralığında diferansiyellenebilir olsun. Buna göre y =
f (x) fonksiyonunun graﬁği üzerindeki her x ∈ (a, b) noktasının düşey olmayan
bir teğeti vardır. Aynı zamanda, y = f (x) fonksiyonunun yansıması olan y =
f −1 (x) ters fonksiyonunun graﬁği üzerindeki f (a) ve f (b) aralığında yer alan
her x noktasının da düşey olmayan bir teğeti mevcuttur. Dolayısıyla y = f −1
fonksiyonu bu x noktalarında diferansiyellenebilirdir. f (f −1 (x)) = x olduğuna
d
f (f −1 (x)) = 1 elde edilir.
göre bu ifadenin her iki tarafından türev alırsak dx
Dolayısıyla burada Zincir Kuralı kullanılır ise
f ′ (f −1 (x))
d −1
1
d −1
f (x) = 1 yani
f (x) = ′ −1
dx
dx
f (f (x))
sonucuna ulaşılır.
Teorem 4.7.2 (Ters Fonksiyon Teoremi). I bir açık aralık ve f : I → R
fonksiyonu 1-1, sürekli olsun. Eğer a ∈ I için b = f (a) sağlanıyor ve f ′ (a) türev
değeri mevcut ve sıfırdan farklı ise buna göre f −1 ters fonksiyonu b noktasında
diferansiyellenebilirdir ve (f −1 )′ (b) = 1/f ′ (a) eşitliği geçerlidir.
Örnek 4.7.3. f (x) = 2x + cos x ise (f −1 )′ (1) değerini hesaplayınız.
Çözüm. Her x ∈ R için
f ′ (x) = 2 − sin x > 0
olduğundan f fonksiyonu R üzerinde 1-1 ve artandır. (f −1 )′ için bir ifade bulmadan (f −1 )′ (1) değerini hesaplayabiliriz. f (0) = 1 olduğundan f −1 (1) = 0
eşitliği gerçeklenir. Buna göre Teorem 4.7.2 kullanılarak
(f −1 )′ (1) =
1
1
1
1
= ′
=
=
f ′ (f −1 (1))
f (0)
2 − sin 0
2
elde edilir.
Örnek 4.7.4. f (x) = x3 + x ise (f −1 )′ (10) değerini hesaplayınız.
Çözüm. Her x ∈ R için
f ′ (x) = 3x2 + 1 > 0
olduğundan f fonksiyonu R üzerinde 1-1 ve artandır. (f −1 )′ için bir ifade bulmadan yukarıdaki şekilde hareket ederek (f −1 )′ (1) değerini hesaplayabiliriz.
f (2) = 10 olduğundan f −1 (10) = 2 eşitliği gerçeklenir. Buna göre Teorem 4.7.2
kullanılarak
(f −1 )′ (10) =
1
1
1
1
= ′
= 2
=
f ′ (f −1 (10))
f (2)
32 + 1
13
elde edilir.
135

mb1001 analiz ı - İstanbul Kültür Üniversitesi

Related documents

Products

Support

mb1001 analiz ı - İstanbul Kültür Üniversitesi

Related documents

Add this document to collection(s)

Add this document to saved

Suggest us how to improve StudyLib