Mekanik, Statik Denge

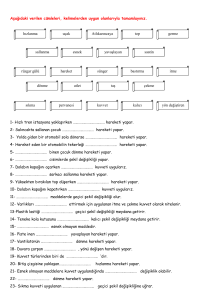
Mekanik, Statik Denge
Mardin Artuklu Üniversitesi
2. Hafta-01.03.2012
İdris Bedirhanoğlu
url : www.dicle.edu.tr/A/idrisb
e-mail : idrisbed@gmail.com
0532 657 14 31
Statik
**Statik; uzayda kuvvetler etkisi altındaki cisimlerin denge konumunu inceler.
**Bir cisim bir koordinat sistemine göre hareket etmiyorsa veya düzgün
doğrusal (sabit hızlı) bir hareket yapıyorsa dengededir.
**Cismin
denge konumunu bozan veya bozulmuş denge konumunu tekrar
dengeye getiren etkiye kuvvet denir.
**Bir
kuvvet; şiddeti, uygulama noktası, doğrultusu ve yönü ile karakterize
edilir.
(Uygulama noktası)
P= 5 ton (Şiddeti)
(Yönü)
(Doğrultusu)
**Kuvvet bir cisme başka bir cismin teması veya yerçekimi kuvvetinde olduğu
gibi uzaktan etkir.
KUVVET :
Özetle;
Herhangi bir yerdeğiştirmenin nedeni olarak düşünülen etkinin
matematiksel modeli diye düşünebiliriz.
Kuvvet = vektörel bir büyüklüktür
ETKİ
TEPKİ
**Kuvvet
temas ile etkirse ve temas yüzeyi küçükse kuvvet bir
noktaya uygulanıyor kabul edilir ve tekil kuvvet adını alır.
Kuvvet etki ettiği temas yüzeyi büyükse kuvvetin bu yüzey
üzerine yayılı etkidiği kabul edilir.
q= 5 t/m
(Yayılı kuvvet)
(Tekil kuvvet)
P= 5 ton
(Temas yüzeyi)
P= 40 ton
q= 5 t/m
8m
(Yayılı kuvvet)
4m
A
(Tekil kuvvet)
4m
**Kuvvet hacim üzerinde yayılı fakat tek bir noktaya etkidiği varsayılır;
Ağırlık Merkezi (G).
w2
w1
=
G
wn
G
n
W = ∑ wi
i =1
W
**Bir cisme etki eden kuvvet başka bir cisim tarafından etki
ettirilirse böyle kuvvete dış kuvvet denir.
**Bir cismin kendi parçalarının arasındaki kuvvete ise iç kuvvet
denir.
F3
F1
Aynı cismi iki parçaya
ayırdığımızı kabul edelim
F2
Fn
A
Dış kuvvet
B
B
A
İç kuvvet
Statiğin Temel İlkeleri
I. İlke (Paralelkenar ilkesi):
**Bir rijit cisimde bir noktaya etki eden iki kuvvetin yerine bir kuvvet
konulabilir. Bu kuvvet, kenarları verilen kuvvetlere eşit olan
paralelkenarın köşegeni çizilerek elde edilir ve bu iki kuvvetin bileşkesi
adı verilir.
II. İlke (Denge ilkesi):
**Bir
rijit cisme etki eden iki kuvvetin dengede olabilmeleri için
tesir çizgilerinin (doğrultularının) aynı, şiddetlerinin eşit ve
yönlerinin zıt olması gerekir.
Rijit cisim
P1 = P 2
P1
P2
III. İlke (Süperpozisyon İlkesi):
**Rijit bir cisme etkiyen bir kuvvet sistemine dengedeki bir
kuvvet sistemini eklemek veya çıkarmak rijit cismin durumunu
değiştirmez.
P2
C
P1
P2
≡
B
P1
C
A
B
≡
P1
C
P3
A
B
P3
IV. İlke EtkiEtki-tepki İlkesi
**Birbirine
değen herhangi bir A ve B cisimleri karşılıklı olarak
şiddetleri eşit, doğrultuları aynı, yönleri ters kuvvet uygularlar.
Eğer bu cisimler arasında sürtünme yoksa bu kuvvetler değme
yüzeyine dik doğrultudadır.
RA= -RB
RA
RB
Değme yüzeyi
Uzay :
**İncelenecek olayın ortaya çıktığı geometrik bölgeye denir.
z
P(x,y,z)
O
x
y
Birimler:
10 N (Newton)= 9,81 kg= 1 kgm/s2
Kuvvetin birimi Newton olup; 1 Newton 1 kg’lık kütleyi 1 m/s2 ‘lik ivme
kazandıran büyüklüktür.
1 N’luk kuvvetin 1 m2’lik alanda yaratacağı etki (gerilme) 1 paskal’dır.
1 Pa= 1 N/m2
1 MPa =1N/mm2
Metre : Dünyanın çevresinin yaklaşık 40 milyonda biri.
Saniye : Ortalama güneş gününün 86400’de biri.
Kilogram : 1 litre normal suyun ağırlığı.
Kütle : kg.s2/m
Vektörler:
1- Serbest vektör
2- Kayan vektör
3- Sabit vektör
4- Birim vektör
Vektör; şiddet, doğrultu ve yön belirtir.
Y
Doğrultusu
Şiddeti
Yönü
F
Uygulama noktası
A(xA ,yA)
B(xB ,yB )
F vektörü
O (0,0) (Referans noktası)
X
1- Serbest vektör
Kuvvet çiftinin moment etkisi serbest vektördür
F= 5 ton
F= 2 ton
M= 10 tm
=
=
F= 2 ton
F= 5 ton
2- Kayan vektör
Doğrultusu
F
F
A
B
=
A
F
=
B
-F
F vektörü kayan vektördür
A
F
B
3- Sabit vektör
F= 5 ton
A
4- Birim vektör
Boyu 1 birim olan vektördür.
Z
λzk
λ
O
λxi
X
λyj
UYGULAMA
Y
B
F
40 m
80 m
A
30 m
O
X
OB kulesi A noktasına AB kablosu ile bağlıdır.
Kablodaki kuvvet F=1200 kg.
A)Kuvvetin Fx,Fy,Fz bileşenlerini,
B) θx, θy, θz açılarını hesaplayınız.
AĞIRLIK MERKEZİ (SENTROİD)
İki Boyutlu Cisimlerin Ağırlık Merkezi
Dünyanın rijit cisme uyguladığı yerçekimi tek bir W
(Weight=ağırlık) kuvveti ile gösterilebilir. Cismin
ağırlığı denilen bu kuvvetin uygulama noktası
cismin ağırlık merkezidir.
G(XG ,YG , ZG) noktası ağırlık merkezinin uygulama
noktasıdır.
Alanların (İki Boyutlu Cisimlerin) Ağırlık
Merkezi Hesabı
Üniform kalınlıklı homojen bir plak elemanın ağırlığı aşağıdaki
hesaplanabilir :
∆W = γ .t.∆A
∆W
t
∆A= ∆a × ∆b
∆A
b
a
Burada γ ; malzemenin özgül (birim hacim) ağırlığı
(t/cm3, t/m3…), t plağın ağırlığı (cm,mm..) ∆A gözönüne
alınan eleman parçasının alanı (cm2,mm2…) olup ∆W
birimi (t, kg….) olur.
Çok kullanılan bazı alanların ve tellerin ağırlık merkezleri
Üçgen
xG=x/3
y
G(xG,yG)
yG
yG=y/3
Alan=x.y/2
xG
x