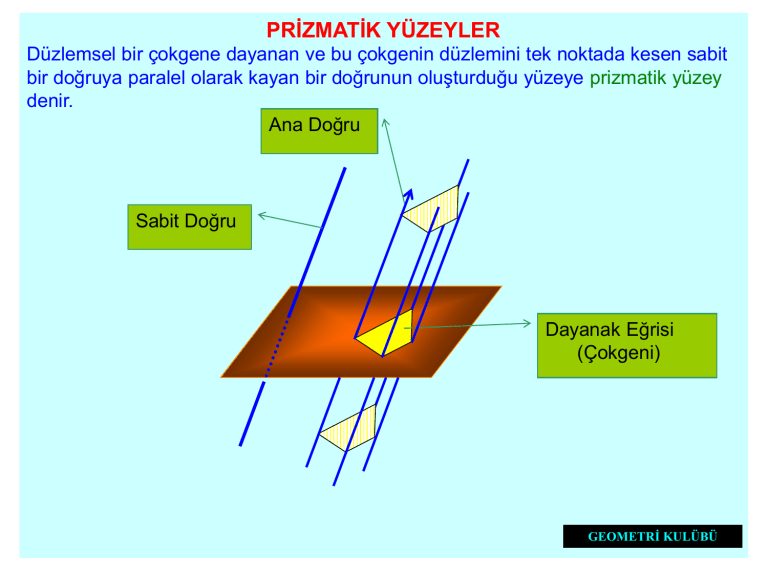
PRİZMATİK YÜZEYLER
Düzlemsel bir çokgene dayanan ve bu çokgenin düzlemini tek noktada kesen sabit
bir doğruya paralel olarak kayan bir doğrunun oluşturduğu yüzeye prizmatik yüzey
denir.
Ana Doğru
Sabit Doğru
Dayanak Eğrisi
(Çokgeni)
GEOMETRİ KULÜBÜ
PRİZMA
Bir prizmatik yüzeyin ana doğrularını kesen iki paralel düzlemle, prizmatik yüzey
arasında kalan kapalı cisme prizma denir.
SONUÇLAR
1. Yanal yüzler paralelkenardır.
2. Alt ve üst tabanlar eştir.
Alt ve üst tabanlar arasındaki
uzaklığa prizmanın yüksekliği
denir.
ÜST TABAN
DİK KESİT
3. Tabanı n-gen olan bir prizmanın n tane
yan yüzü vardır.
YANAL
AYRIT
4 .Tabanı n-gen olan prizmaya
n-gen prizma denir.
(Üçgen prizma, Beşgen prizma, Düzgün
altıgen prizma ...)
5. Ayrıca prizmalar yan
ayrıtlarının tabana dik olup
olmamasına göre ;
- dik n-gen prizma
- eğik n-gen prizma olarak
adlandırılır.
YANAL YÜZ
ALT
TABAN
TABAN AYRITI
GEOMETRİ KULÜBÜ
DİK PRİZMALARIN ÖZELİKLERİ
GEOMETRİ KULÜBÜ
1. Dik prizmaların yan yüzeyleri dikdörtgendir.
2. Dik prizmalarda yan ayrıtların uzunluğu prizmanın yüksekliğine eşittir.
PRİZMALARIN İSİMLENDİRİLMESİ
1. EĞİK PRİZMA
2. DİK PRİZMA
3. DÜZGÜN PRİZMA ?
4. ÖZEL PRİZMALAR ?
3. DÜZGÜN PRİZMA
Tabanları düzgün çokgen olan dik prizmaya düzgün prizma denir.
*** Düzgün prizmaların yan yüzleri bir birine eş olan dikdörtgenlerdir.
ÖZEL PRİZMALAR
Paralelyüz
Dik paralelyüz
GEOMETRİ KULÜBÜ
SONUÇLAR
.Paralelyüzün tüm yüzeyleri
birer paralelkenardır.
.Dik paralelyüzün sadece
tabanları paralelkenardır. Yan
yüzleri dikdörtgendir.
Dikdörtgenler prizması
Küp
.Dikdörtgenler prizmasının tüm
yüzeyleri dikdörtgendir.
.Kübün tüm yüzeyleri karedir.
.Silindirin tabanı dairedir.
Dairesel eğik silindir
Dik silindir
EĞİK VE DİK PRİZMALARIN KARŞILAŞTIRILMASI
Herhangi bir eğik prizmanın dik kesiti alınarak, alt ve üst
tabanları üst üste getirilirse dik prizma elde edilir.
*** Her iki prizmanın hacimleri eşittir.
.
SONUÇ
*** Dik prizmalarda yükseklik yan ayrıta eşittir.
*** Dik prizmalarda taban bir dik kesittir.
GEOMETRİ KULÜBÜ
GEOMETRİ KULÜBÜ
PRİZMANIN YANAL ALANI
A’
1.Prizmanın yanal alanı : “Yan yüzeylerin alanları toplamı”
D’
B’
K
C
N
YANAL ALAN = YANAL AYRIT UZUNLUĞU x DİK KESİT ÇEVRESİ
SY=L . ÇD
2.Dik prizmanın yanal alanı :
YANAL ALAN = YÜKSEKLİK x TABAN ÇEVRESİ
SY=h . ÇT
3. Prizmanın Alanı : “Tüm alanı”
PRİZMANIN ALANI = YANAL ALAN + 2 x TABAN ALANI
S = SY + 2 ST
L
A
M
D
B
C
PARALELYÜZÜN ÖZELİKLERİ
1. O simetri merkezidir.
2. S=2 x (Üç paralelkenar alanı)
3. Cisim köşegeni : Bir köşe ile buna komşu olmayan köşeyi birleştiren doğru
parçasıdır.
4. Cisim köşegenlerinin hepsi farklı uzunluktadır.
AC’A’C
C’
A’
O
D
C
A
B
GEOMETRİ KULÜBÜ
PRİZMANIN HACMİ
GEOMETRİ KULÜBÜ
TEOREM
Bir dikdörtgenler prizmasının hacmi bir köşeden geçen üç
ayrıtının uzunlukları çarpımına eşittir.
SONUÇ
Dikdörtgenler prizmasının hacmi :
c
Taban alanı ile yüksekliğin
çarpımına eşittir.
b
V=ST . h
a
V= a.b.c
KÜBÜN HACMİ : Bir ayrıtı a br. olan kübün hacmi a3 birimküptür.
a
a
a
GEOMETRİ KULÜBÜ
SONUÇ 1 : Tabanı diküçgen olan herhangi bir dik prizmanın hacmi ; V=ST . h dır.
Şekildeki üçgen prizma ters çevrilerek ilk verilen
prizmaya yapıştırılırsa bir dikdörtgenler prizması elde
edilir.
b
Elde edilen dikdörtgenler
prizmasının hacmi ilk verilen dik
prizmanın hacminin iki katıdır.
h
a
V
a.b.h a.b
.h S T .h
2
2
Tabanı herhangi bir üçgen olan dik prizmanın hacmi de V= ST . H dır. Çünkü verilen
prizma tabanları dik üçgen olan iki prizmaya bölünebilir.
S1
,
V1
S2 , V2
h
V=V1+V2=S1.h+S2.h=(S1+S2).h=ST . h
GEOMETRİ KULÜBÜ
Tabanı herhangi bir çokgen olan dik prizmanın hacmi de V=ST . h dır.
S1
,
S3
V1
S2
,
,
V3
V3
V=V1+V2+V3
=S1.h+S2.h+S3.h
=(S1+S2+S3).h
=ST .h
Herhangi bir dik prizmanın hacmi tabanı ile yüksekliğinin çarpımına eşittir.
GEOMETRİ KULÜBÜ
Herhangi bir eğik prizmanın hacmi ; Dik kesit alanı ile yan ayrıt uzunluğu çarpımına eşittir.
Herhangi bir dik prizmanın hacmi ; Taban alanıı (dik kesit alanı) ile yüksekliği
(yanayrıt) uzunluğu çarpımına eşittir.
Prizma Hacmi=Dikkesit alanı x yan ayrıt uzunluğu
GEOMETRİ KULÜBÜ
GEOMETRİ KULÜBÜ
PRİZMA AÇILIMLARI












