(Microsoft PowerPoint - KATI C\335S\335MLER

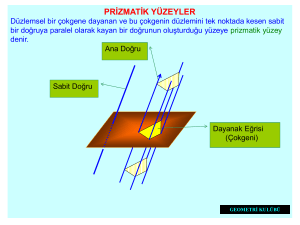
UZAY GEOMETRİ HAKKINDA GENEL HATIRLATMALAR
UZAY AKSİ
AKSİYOMLARI
ÜÇ DİKME TEOREMİ
TEOREMİ
Farklı iki noktadan bir tek doğru geçer.
Katı cisim sorularını çözmede çok faydalı bir bilgidir.
A
Doğrusal olmayan 3 farklı noktadan bir tek düzlem
geçer
{B, C, D, H } ∈ E
Bir doğru ve bu doğru üzerinde bulunmayan bir
.H
nokta düzlem belirtir.
[AH] ⊥ [HC]
.
B
E
C
[HC] ⊥ [BD] ise
D
[AC] ⊥ [BD] olur.
Kesişen farklı iki doğru bir düzlem belirtir
Paralel iki doğru bir düzlem belirtir
Farklı iki düzlem kesişirse arakesitleri bir doğrudur.
A
Bir doğru üzerinde bulunmadığı bir düzlemi keserse
{B, C, D, H } ∈ E
arakesiti bir noktadır.
.H
Bir doğrunun farklı iki noktası bir düzlem üzerinde
B
E
ise, bu doğrunun bütün noktaları da bu düzlem
C
[AH] ⊥ [HC] ve
.
[AC] ⊥ [BD] ise
D
[HC] ⊥ [BD]
eks TR em yayınları
üzerindedir.
Paralel iki düzlemden biri içindeki her doğru diğer
düzleme paraleldir.
Paralel iki düzlemden birini kesen bir düzlem
diğerini de keser.
Üç dikme teoremi ile birçok katı cisim sorusunda
karşılaşılabilir. Birkaç örnek verelim…
Kesişen iki düzlemin ikisine de paralel olan bir
Silindir
Dikdörtgenler prizması
doğru bu düzlemlerin arakesit doğrusuna da
H
paraleldir.
G
E
C
D
F
Aynı doğruya paralel olan iki doğru birbirine
paraleldir.
C
D
B
A
Bir düzlemin kesişen iki doğrusuna kesişme
O
A
B
E
[DE] ⊥ [EB]
[HA] ⊥ [AB]
noktasında dik olan doğru bu düzleme diktir.
Aynı doğruya dik olan iki düzlem birbirine paraleldir
Yanda düzgün altıgen şeklinde
lamba
Aynı düzleme dik olan iki doğru birbirine paraleldir.
K
Bir noktadan geçen ve bir doğruya dik olan yalnız
Direk üzerinde alınan herhangi
E
B
bir düzlem vardır.
lamba direği dikilmiş olsun.
.F
A
düz bir arsanın F köşesine bir
bir K noktasından A noktasına
çizilen doğru parçası AC ye dik
C
Paralel iki düzlemden birine dik olan doğru diğer
D
olur.
Yani [KA] ⊥ [AC]
düzlemede diktir.
221
celal.isbilir@gmail.com
KATI CİSİMLER HAKKINDA GENEL HATIRLATMALAR
KATI Cİ
CİSİMLER 3 ANA BAŞ
BAŞLIK ALTINDA
ÜÇGEN
ÜÇGEN PRİ
PRİZMA
A’
İNCELENEBİ
NCELENEBİLİR:
A’
C’ Yan yatmış hali
.
PRİZMALAR: (Dikdörtgenler prizması, kare prizma, küp,
B’
üçgen prizma, silindir, beşgen prizma, yamuk prizma…)
B’
C’
A
PİRAMİTLER: (Üçgen piramit, kare piramit, yamuk piramit,
A
koni… )
.
C
C
.
KÜRE:
B
B
Yukarıdaki dik üçgen prizmalar dikkatlice incelenirse aynı
PRİ
PRİZMALAR
cismin farklı perspektiften görünen eş iki üçgen prizma
olduğu görülür. Fakat ikinci şeklin hacmini hesaplarken
HACİM : Taban alanı x Yükseklik
bazen taban alanı hangisi diye bir problemle karşılaşan
YANAL ALAN: Taban çevresi x Yükseklik
öğrenciler şeklin ilk konumunu göz önüne alırlarsa hacmi
Eğer prizma dik ise, yanal alan(lar) dikdörtgendir.
daha kolay hesaplayabilirler.
YÜZEY ALANI (ALANI ): Yanal alan + 2(Taban alan)
SİLİNDİ
NDİR (dairesel prizma)
DİKDÖ
KDÖRTGENLER PRİ
PRİZMASI
a, b, c ......: Ayrıtlar (kenarlar)
e...............: Cisim köşegeni
f.................: Bir yüzey köşegeni
Hacim = V = a.b.c
G
Yanal alan = 2(a + b).c
F
E
c
e
Alan = 2(a.b + a.c + b.c)
b
a
A
r
B
2πr
AN
AL
L
NA
YA
r
O
Yanal alan = 2π
π.r.h
V = π.r2.h
Tüm alan = 2π
π.r.h + 2π
π.r2
PİRAMİ
RAMİT
f = a2 + b2
B
.O
A
C
f
r
O
h
e = a 2 + b2 + c 2
D.
C
h
eks TR em yayınları
H
.O` r
D
Dikdö
Dikdörtgenler prizması
prizmasında: 12 tane ayrıt, 8 tane köşe,
DİK PİRAMİT: Cisim yüksekliği tabanın ağırlık
merkezinden geçer.
12 tane yüzey köşegeni ve 4 tane cisim köşegeni vardır.
DÜZGÜN PİRAMİT: Cisim yüksekliği tabanın ağırlık
merkezinden geçer, ayrıca tabanı düzgün çokgendir.
KARE PRİ
PRİZMA
NOT: Düzgün piramit aynı zamanda dik piramittir.
KÜP
G
H
H
F
E
Yan yüz yüksekliği
e
D
A
a
a
h
C
f
A
a
a
Cisim yüksekliği
(hacim hesaplarken kullanılır)
D
.
.
B
H
B
Hacim = V = a2.b
Yanal alan = 4a.b
Alan = 4a.b + 2a2
e = 2a2 + b2
C
(alan hesaplarken kullanılır)
a
b
D
T
F
E
e
KARE DİK Pİ
PİRAMİ
RAMİT
G
Hacim = V =
a3
A
Yanal alan = 4a2
a
B
Alan = 6a2
(taban alanı).h a2 .h
Hacim V =
=
3
3
e=a 3
Yanal alan = Şekli saran 4 üçgenin alanı
f =a 2
Alan = yanal alan + a2
222
celal.isbilir@gmail.com
Katı cisimler hakkında genel hatırlatmalar
BENZER İKİ
PİRAMİ
RAMİTTE HACİ
HACİMLER
ORANI:
KESİ
KESİK Pİ
PİRAMİ
RAMİT
T
H
F
E
D
4S
V=
O`
A
19V
Hacimler oranı
oranı benzerlik
oranı
oranının kü
küpüne eş
eşittir.
h
a
C
a
r
ÜST
TABAN
yanal alan
a3 2
12
S=
2πr '+ 2πr .
| DC |
2
a 6
h=
3
G
a
D
2πr
ALT
TABAN
alt taban alanı
alanı
πr2
C
YANAL ALAN
A = a2 3
H
B
DÜZGÜ
ZGÜN SEKİ
SEKİZYÜ
ZYÜZLÜ
ZLÜ
Tüm ayrıtları eşit olan iki tane kare piramidin
tabanlarının birleştirilmesi ile elde edilen piramittir.
P
eks TR em yayınları
A
açık hali
C
2πr`
Tüm yüzeyleri eşkenar üçgen olan piramittir.
T
a
D
üst taban alanı
alanı
πr`2
DÜZGÜ
ZGÜN DÖ
DÖRTYÜ
RTYÜZLÜ
ZLÜ
a
r`
.
O
B
V=
π.r 2 .h
3
h
9S
B
Tüm alan = π.r. l + π.r2
7V
S
A
α
r
=
360º
l
KESİ
ESİK KONİ
KONİ
V
G
Yanal alan = π.r.l
BENZER İKİ KONİ
KONİDE HACİ
HACİMLER ORANI:
A
V
h=a 2
A
a
A = 2a2 3
C
a
a
a3 2
V=
3
9S
a
D
16S
B
B
C
O
a
a
7V
4S
a
a
a
Hacimler
oranıı
oran
benzerlik
19V
oranıının
oran
37V küpüne e
eşşittir.
S
ÜÇGEN
ÜÇGENİ
GENİN Bİ
BİR KENARI ETRAFINDA DÖ
DÖNMESİ
NMESİ
a
a
a
Alanı S birim kare olan bir
A
ABC üçgeninin [BC], [AC],
P’
DİK (DÖ
(DÖNEL) KONİ
KONİ
c
KONİ
KONİNİN AÇ
AÇILIMI
döndürülmesi ile elde edilen
A
A
α
l
B
l
h
o
[AB] kenarları etrafında 360°
b
r
l
C
l......; koninin ana doğrusu
Yanal alan
l
V[BC] =
(π.r.l )
cisimlerin hacimleri:
a
B
C
4πS2
3a
V[ AC] =
4πS2
3b
V[ AB] =
4πS2
3c
KÜRE
2πr
O r
A
h ......; koninin yüksekliği
o
4
3
V= π. r 3
r
B
Alan = 4.π.r2
r ......; koninin taban yarıçapı
223
celal.isbilir@gmail.com
PRİZMALAR ÜZERİNDE EN KISA YOL
Kırık Çizgileri Dü
Düzleş
zleştirelim
Açık hali
A
b
h2
.
.
A
mi n
(a+
b
h1+h2
h1
Açık hali
G
A
B
a
H
5
F
)
c
dikeyde alınan yol
c
D
B
T
a
A
yatayda alınan yol
mi n
K
c
.
c
E
.
C
( |A
T|+
|TK
|+|K
H|)
a+b+a
H
b
B
Açık hali
6
G Açık hali
F
mi n
c
c
D
P
A
+ |P
G| )
a+b
b
(a + b) + c
c+b
( |A
P|
a
H
A
E
F
P
( |A
P|
c
D
.
A
D
K
M
A
+ |P
G| )
L
C
|)
a
B
.
b
G
|G
1 K| +
|K
c
.
C
L| +
|LM
|+|M
G|
2 )
a+b
G2
b
H
Açık hali
G
A
F
T
c
c
2
C
H
( |A
P|
.
( |A
P|
+ |P
T|)
a+b
b
G
L
T
Açık hali
A
E
+ |P
G| )
a
mi n
A
B
a
c 2
2
|AP| + |PT| toplamının en küçük değeri: ( ) + (a + b)
2
K
F
c
c
G
B
|AP| + |PG| toplamının en küçük değeri:
min
(
B
E
(a + b)2 + c 2
mi n
b +c
P
a
.
G2
c
9
F
A
.
G1
G Açık hali
D
F
D
c
|MB
G
P
H
E
a
G1
B
|AP| + |PG| toplamının en küçük değeri:
4
H
8
a+b
b
a
|+
|G1K| + |KL| + |LM| + |MG2| toplamının en küçük değeri: c 2 + (a + b)2
mi n
c
C
|LM
G1 ve G2 bulundukları yüzeylerin ağırlık merkezleri
Açık hali
G
|+
B
E
(c + b)2 + c 2
|AP| + |PG| toplamının en küçük değeri:
A
G
B
a
3
+ |P
G| )
a
b
A
|KL
|AK| + |KL| + |LM| + |MB| toplamının en küçük değeri: a2 + 4(b + c)2
eks TR em yayınları
mi n
.
C
.
|+
Açık hali
c
D
|AK
2
7
F
C
Açık hali
G
P
M
min
(
b
A
A
E
F
G
2
|AP| + |PG| toplamının en küçük değeri:
H
K
c
B
a
2
( |A
P|
E
D
.
C
G
L
A
A
E
H
c + b+ c + b
H
1
D
T
C
b
mi n
( |A
T|+
|TK
|+|K
a+b+
a
2
L|)
L
a
A
B
3a
2
2
|AT| + |TK|+ |KL| toplamının en küçük değeri: ( + b) + c
2
(b + c)2 + b2
224
celal.isbilir@gmail.com
KONİ YÜZEYİ ÜZERİNDEN EN KISA YOL
Dü
zleşştirelim
Eğri Çizgileri D
üzle
.P
P
1
Açık hali
1
P
1
60°° 60°°
4
F
8
P
Açık hali
5
9
D
4
F
D
A
7
5
A
A
B
2
O
.
O
4
.
A
8
A
B
.
O
3
B
P
Açık hali
7
P
5
O
P
Açık hali
60°° 60°°
8
120° 3
15
E
12
E
.
B
8
3
P
3
.O
A
eks TR em yayınları
B
3
D
8
A
A
.P
D
8
.
16
8
E
D
O
D
8
D
D
9
7
A
.
O
A
A
A
B
B
4
.
Açık hali
9
30° 9
P
.
O
20
D
8
D
A
2
36°° 36°°
8
E
A
A
5
P
Açık hali
D
15
B
5
.
8
24
E
.
A
B
O
P
P
O
A
4
O
4
3
Açık hali
P
4
12
A
B
B
3
O
6
.
Açık hali
E
O
A
2
P
P
2
.
A
B
A
B
B
.
O
12
A
.
O
4
A
B
A
B
.
2
O
225
4
celal.isbilir@gmail.com
SİLİNDİR YÜZEYİ ÜZERİNDEN EN KISA YOL
PİRAMİT YÜZEYİ ÜZERİNDEN EN KISA YOL
Eğri Çizgileri Dü
Düzleş
zleştirelim
1
D
.
C
A
Ad
an
D
h
.
.
O
r
ye
e
nk
D
yol
2πr
A
B
m(BTC) = β
C
A
Ad
an
C
h
.
2
ye
e
nk
ısa
πr
T
α+β
α β
D
D
C
.
K
B
r
Açık hali
T
yol
C
K
m
Açık hali
D
.
C
h
E
A
A
.
r
O
h
2
.
B
A
K|
(| A
n
i
+
D|
|K
A
Ad
an
E
ye
e
nk
ısa
yol
2πr
E
m(BTC) = β
3
Açık hali
T
T
α β
2α+β
D
B
.
R
D
R
.
C
K
K
Açık hali
4
D
.
C
A
Ad
an
C
ye
e
h
h
.
A
.
O
r
A
m(ATB) = α
nk
ısa
in
+|
K|
|( A
C
A
Açık hali
T
T
2α+2β
D
R
5
A
Ad
an
P
K
ye
e
h
.
h
πr
A
.
O
nk
ısa
yol
A
m(ATB) = α
.
R
Açık hali
C
|
4
B
.P
|+
KD
|)
DR
m(BTC) = β
yol
3πr
m
B
α β
D
)
m(ATB) = α
eks TR em yayınları
3
C|)
m(ATB) = α
h
A
K
|+|
(|AK
min
D
A
C
.
K
C
B
.
.
O
α+β
K
ısa
Açık hali
2
T
Açık hali
α β
h
A
T
1
Açık hali
B
C
.
K
A
K
(|A
in
m
.
A
)
D
A|
|R
|+
R
D
+|
D|
|K
|+
m(BTC) = β
P
2
r
B
226
celal.isbilir@gmail.com