AST416
Astronomide Sayısal Çözümleme - II
2. Temel İstatistik Kavramlar ve
Dağılımlar
Bu derste neler öğreneceksiniz?
• Sıklık Dağılımı ve Olasılık Dağılımı
• Olasılık ve Kümüatif Dağılım Fonksiyonları
• Dağılım Fonksiyonu Elemanları
• Örnek Dağılım ve Ana Dağılım (Sample Dist. & Parent Dist.)
• Tekdüze Dağılım (Uniform Dist.)
• Normal/Gauss Dağılım (Normal/Gaussian Dist.)
• Log-Normal Dağılım
• Pareto Dağılımı
• Binom ve Bernoulli Dağılımları
• Poisson Dağılımı
• Üstel Dağılım (Exponential Dist.)
• Gamma Dağılımı
• Lorentz Dağılımı (Cauchy Dağılımı)
• Ki-kare Dağılımı (Chi-squared Dist.)
• Öğrencinin t Dağılımı (Student’s t Dist.)
• F Dağılımı
• Beta Dağılımı
Dağılım?
Olasılık teorisi terminolojisi henüz tam olarak yerleşmiş
sayılmaz. Aşağıdaki terimlerin birbirleri yerine kullanıldığını
görebilirsiniz.
•
•
•
•
•
•
•
Sıklık dağılımı (Frequency distribution)
Olasılık dağılımı (Probability dist.)
Dağılım fonksiyonu (Distribution function)
Olasılık dağılım fonksiyonu (Probability distribution func.)
Olasılık kütle fonksiyonu (Probability mass func.)
Olasılık yoğunluk fonksiyonu (Probability density func.)
Olasılık fonksiyonu (Probability func)
Sıklık Dağılımı ve Olasılık Dağılımı
Sıklık dağılımı (frequency distribution),
bir örnek grubunda (Örn. ölçümler)
sonuçların ne miktarda olduğunun
gösterilmesidir.
Boy (m)
Öğrenci Sayısı
Kümülatif Sayı
< 1.6
6
6
1.6 – 1.8
12
18
1.8 – 2.0
10
28
2.0 <
3
31
Olasılık dağılımı (probability dist.), bir deney
sonucunun
gerçekleşme
ihtimalinin
gösterilmesidir.
Para Fırlatma
Sayısı
Yazı Gelme
Sayısı
Yazı Gelme
İhtimali
4
1
%25
100
66
%66
1000
589
%58.9
10000
4882
%48.82
Öğrenci Boyları Dağılımı
14
12
10
8
6
4
2
0
Yazı Gelme Olasılığı Dağılımı
70
60
50
40
30
20
10
0
Para Fırlatma Sayısı
Boy
< 1.6
1.6 - 1.8
1.8 - 2.0
2.0 <
4
100
1000
10000
Olasılık Yoğunluğu Fonksiyonu
(Probability Dens. Func.)
Bir deney sonucunun gerçekleşme olasılığını veren fonksiyondur. Herhangi bir olguya
ilişkin ölçümlerin dağılımı, olgunun sahip olabileceği değerlerin gerçek olma ihtimali
olarak da düşünülebilir. Normalize olasılık dağılım fonksiyonlarında her bir ölçüme
ilişkin olasılık değerlerinin toplamı 1 değerine normalize edilir.
Bir kablosuz haberleşme hattındaki
sinyalin zayıflama profili ve matematiksel
ifadesi. (Gamma dağılımı)
200 defa fırlatılan bir parada yazı gelmesinin
olasılık kütle fonksiyonu grafiği ve
matematiksel ifadesi. (Binom dağılımı)
Kümülatif / Birikimli Dağılım
Fonksiyonu (Cumulative Dist. Func.)
Olasılık dağılım fonksiyonunun sahip olduğu değerlerin
toplanarak temsil edildiği fonksiyonlardır. Olasılık değerlerinin
tamamı 1 ya da %100 ihtimale sahip olduğu için 1 değerine
yakınsamaktadır.
Dağılım Fonksiyonu Elemanları
Dağılım fonksiyonlarının yapısını belirleyen elemanlar
bulunmaktadır. Bu elemanlar:
• Ortalama değer (Average/Weighted Average/Mean)
• Varyans (Variance)
• Çarpıklık (Skewness)
• Basıklık (Kurtosis)
Ortalama Değer / Beklenen Değer
Bir dağılımın ortalama değeri, bu dağılımı oluşturan ölçümlerin
doğruluğunu belirlemektedir.
Beklenen değerden farklılık gösteren ortalama değerler sistematik
hatalardan kaynaklanabileceği gibi, beklenen değerin gerçek değer
olmamasından (örn. Teorik hesapların eksik/yanlış olmasından) ya
da yeterli ölçümün yapılmamasından kaynaklanabilir.
Doğruluk
Ortalama Değer / Beklenen Değer
X değeri için yapılan farklı
sayıda
ölçümlerin
histogramları. Sırasıyla 5, 50,
100,
1000
defa
ölçüm
yapılmıştır.
Ölçüm
sayısı
arttıkça,
dağılımın
yapısı
belirginleşmiş, ortalama değeri
ve ortalama değer etrafındaki
saçılma belirginleşmiştir.
Ortalama Değer / Beklenen Değer
Özellikle simetrik olmayan dağılımlar söz
konusu olduğunda, tercihe göre beklenen
değer olarak ortalama değer yerine mod ya
da medyan değeri kullanılabilmektedir. Bu
tercih gözlenen/ölçülen olgunun türüne
göre yapılabilmektedir.
Örneğin gelir dağılımı, az sayıda yüksek
gelirli bir grubun olması sebebiyle, yüksek
gelir bölgesine doğru kaymış bir ortalama
değer verecektir. Bu sebeple insanların
büyük bir kısmı ortalama gelirden daha
düşük gelire sahip olmaktadır.
Varyans ve Standart Sapma
(Variance & Standard Deviation)
Varyans ve standart sapma (σ), dağılım değerlerinin ortalama değer
etrafında ne kadar çok saçılmış olduğunu belirler. Dolayısıyla yapılan
ölçümlerin ne kadar hassas olduğunu belirlemektedir.
Varyans ve Standart Sapma
(Variance & Standard Deviation)
Varyansın bazı özellikleri
• Varyans ve standart sapma değerleri negatif olamaz.
• Tüm ölçümler aynı değere sahip ise varyans sıfır değerini alır.
• Varyans değeri, dağılımın konumundan bağımsızdır. Tüm değerler
aynı miktarda kaydırıldığında varyans değişmez.
• Varyansın birimi, ölçülen değerin biriminin karesidir. Standart
sapmanın birimi ise ölçülen değerin birimidir.
Varyans ve Standart Sapma
(Variance & Standard Deviation)
Çarpıklık (Skewness)
Bir dağılımın asimetrisinin ölçütüdür. Bu ölçütün
basit ve standart bir matematiksel ifadesi yoktur.
Temel olarak iki tür çarpıklık vardır.
Negatif Çarpıklık: dağılımın sol kuyruğu uzundur;
dağılımın önemli bir çoğunluğu sağ tarafta
toplanmıştır.
Pozitif Çarpıklık: dağılımın sağ kuyruğu uzundur;
dağılımın önemli bir çoğunluğu sol tarafta
toplanmıştır.
Çarpıklık (Skewness)
Farklı çarpıklıklara sahip iki adet
log-normal dağılımdaki mod,
medyan ve ortalama değerlerin
karşılaştırması.
Basıklık (Kurtosis)
Bir dağılımın ne kadar geniş
olduğunun ya da ‘kuyruklu’
olmasının ölçütüdür. Çarpıklık
gibi basit ve standart bir
matematiksel ifadesi yoktur.
Örnek Dağılımı ve Ana Dağılım
(Sample Dist. & Parent Dist.)
Yapılan gözlemlerin sayısının arttırılması, gözlemlerin oluşturduğu dağılımı, ilgili
olgunun gerçek dağılımına daha fazla yaklaştıracaktır. Ancak sonsuz adet gözlem
yapmanın mümkün olmaması sebebiyle yapılan gözlemler gerçek dağılımın bir
örneği niteliğini taşımaktadır.
Bir dağılımı oluşturmak için mümkün olan sonsuz sayıdaki tüm değerlerin
kullanılması kabulu, elde edilen dağılımın ana dağılım olarak kabul edilmesi
anlamına gelmektedir. Gerçekte herhangi bir olayın tam olarak ne tür bir dağılım
gösterdiğini bilemeyiz. Ancak bu dağılımı yeterli hassasiyette temsil ettiği kabul
edilen matematiksel bir fonksiyonu, olgunun ana dağılımı olarak kabul ederiz.
Bu kabulden sonra, yapılan gözlemlerin oluşturduğu ve sonlu sayıdaki değerler ile
üretilen örnek dağılımı kullanarak ana dağılıma ilişkin parametreleri elde edebilir
ya da ana dağılımın geçerliliğini sorgulayabiliriz.
Örnek Dağılımı ve Ana Dağılım
(Sample Dist. & Parent Dist.)
Bir grup öğrenci, bir top ile serbest
düşme deneyi yapıp, topun 2 metrelik
mesafeyi kaç saniyede kat ettiğini
ölçmüşlerdir. 50 defa tekrarlanan bu
deneyin sonunda ölçümleri yandaki
histograma yerleştirmişlerdir.
Bu dağılımın ölçümlerdeki rastgele
hatalardan kaynaklandığı kabulü ile
ortalama değer ve standart sapmasını
hesaplamışlar ve bir Gauss dağılımı
üretip düz çizgi ile histogramın üzerine
çizmişlerdir. Bu eğrinin, ana dağılımı
temsil etmesi beklenmektedir.
Kesikli çizgi ile çizilen eğri ise aynı
deneye ilişkin teorik hesaplamalar ile
elde edilen dağılımı göstermektedir.
Bu iki dağılım arasındaki farklar nelerdir?
Aralarındaki farklar nasıl giderilebilir?
Örnek Dağılımı ve Ana Dağılım
(Sample Dist. & Parent Dist.)
Ana dağılımın ξi olası değeleri için
hesaplanabilen standart sapması yanda
verilmiştir.
Ana dağılımın varlığının kabulu ile artık
bir
ortalama
değer
belirlenmiş
olduğundan, örnek uzayın standart
sapmasının
hesabında
karekök
içerisindeki payda ölçüm sayısından 1
çıkararak hesaplanmalıdır.
Bu hesabın gerekçesi, bir ana dağılımın
varlığı durumunda ortalama değerin
belirlenmiş
olmasıdır.
Dolayısıyla
standart sapma hesaplanırken olası
değerlerin bulunabileceği serbestlik
derecesi 1 eksik olmaktadır.
Tekdüze Dağılım (Uniform Dist.)
Tekdüze dağılım, bir aralık
içerisindeki
değerlerin
tamamının
aynı
olasılıkla
bulunabileceği bir dağılım
türüdür.
Bu dağılım türü bir ön bilgiye
sahip
olunmayan
(uninformative) ya da belirli
değerlerde farklılık göstermesi
beklenmeyen
olguların
dağılımlarını temsil etmek için
kullanılır.
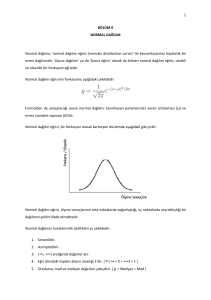
Normal (Gauss) Dağılım
Ölçümlerde rastgele hataların varlığı
sebebiyle oluşan dağılıma normal dağılım
ya da Gauss dağılımı adı verilir.
Doğada gözlenen bir çok olguya ilişkin
ölçümlerin dağılımı Gauss dağılımı ile
temsil edilebilmektedir. Bu sebeple Gauss
dağılımına ‘normal’ adı verilmiştir.
Matematiksel olarak iki parametreye bağlı
bir
dağılım
fonksiyonudur.
Bu
parametreler, ortalama değer ve standart
sapmadır.
Ortalama değerin sıfır ve standart
sapmanın 1 alındığı durumda ‘standart
normal dağılım’ elde edilmektedir.
Merkezi Limit Teoremi (Central
Limit Theorem)
Çoğu
durumda,
bağımsız
rastgele
sonlu
değişkenlerin eklenmesi durumunda, toplamın
dağılımı normal dağılıma yaklaşmaktadır. Buna
merkezi limit teoremi adı verilmektedir. Toplanan bu
değişkenlerin başlangıçtaki dağılımlarının türü
önemsizdir.
Yandaki örnekte 6 yüzlü adil bir zarın n defa atılması
ile
gelen
sayıların
toplamlarının
dağılımı
görülmektedir. Başlangıçta tekdüze dağılım gösteren
bu deney, n sayısı büyüdükçe normal dağılıma
yaklaşmaktadır.
Teorem, farklı bir çok istatistiksel yöntemde, başka
tür dağılımların söz konusu olduğu durumlarda bile
normal dağılım kullanarak yaklaşım yapılabileceği
sonucunu çıkarmaktadır.
Merkezi Limit Teoremi (Central
Limit Theorem)
Bazı dağılımlar için merkezi limit teoremi örnekleri:
• Binom dağılımı B(n,p), ortalama değer np ve
varyans np(1-p) durumlarında, eğer n ve p
yeterince büyük rakamlar ve sıfır ya da bire yakın
değillerse normal dağılıma yakınsar.
• Poisson dağılımı λ parametresinin ortalama değer
ve varyans olduğu ve yeterince büyük olduğu
durumlar için normal dağılıma yakınsar.
• Ki-kare dağılımı, ortalama değer k ve varyansın 2k
olduğu ve k’nin yeterince büyük olduğu durumlarda
normal dağılıma yakınsar.
• Öğrencinin t-dağılımı, ortalamanın sıfır, varyansın 1
olduğu ve v değerinin yeterince büyük olduğu
durumlarda normal dağılıma yakınsar.
Log-Normal Dağılım
Bir
değişimin
logaritmasının
normal
dağılım
göstermesi
durumunda olasılık yoğunluk
fonksiyonu log-normal dağılım
fonksiyonu ile temsil edilir.
Doğada gözlenen olayların önemli
bir kısmı log-normal dağılım
gösterir. Örneğin, büyüyen canlı
doku alanı, Internet tartışma
forumlarında yapılan yorumların
uzunlukları,
parçacık
boyutu
dağılımları, satranç oyununun süre
dağılımı vs.
Pareto Dağılımı
Üstel değişim gösteren bir
dağılımdır. Jeolojik, sosyal ve
bilimsel bir çok farklı alanda
kullanılmaktadır.
Örneğin, harddisk sürücü
hata oranları, yerleşim yeri
boyutları, kum tanelerinin
boyutları, meteorit boyutları,
orman yangınlarında yanan
bölgelerin büyüklükleri vs.
Binom (Binomial) ve Bernoulli
Dağılımları
Binom dağılımı (binomial dist.), n defa
yapılan bir deneyin sonuçlarının
evet/hayır benzeri bir cevabı olması
durumunda başarılı ya da başarısız
deneylerin gerçekleşme ihtimalini
veren dağılımdır.
Deneyin sadece 1 defa yapılmış olması
durumunda olasılık dağılımına Bernoulli
dağılımı adı verilir.
Para atma deneyi birden çok kez
yapılması durumunda binom dağılımı,
sadece 1 kez yapılması durumunda
Bernoulli dağılımı gösterir.
Poisson Dağılımı
Süreksizlik gösteren olayların modellenmesi
için uygun bir dağılım fonksiyonudur. Görece
nadir gerçekleşen ve birbirinden zaman
bağımsız olan olayların olasılığı için
kullanılmaktadır.
Poisson dağılımının kullanılması için 3 gerekli
koşul bulunmaktadır.
1.
Ölçümler
sayısıdır.
nadir
görülen
olayların
2.
Tüm ölçümler birbirinden bağımsızdır.
3.
Ölçümlerin görülme sıklığı ilgili zaman
aralığında değişim göstermemektedir.
Radyoaktif bozulma süreçleri ya da foton
sayımı
süreçleri
Poisson
dağılımı
göstermektedir.
Poisson Dağılımı
Poisson dağılımının, ortalama değeri
değişmesi (sırasıyla 1, 3, 10, 50)
durumundaki değişimi.
Büyük λ değerleri söz konusu
olduğunda (λ > 1000) Poisson
dağılımı, λ ortalamalı ve λ standart
sapmalı bir Gauss profili ile temsil
edilebilmektedir.
Bunun
için
süreklilik düzeltmesi gerekmektedir.
Poisson Dağılımı
Poisson dağılımı gösteren
bir
olayda
ortalama
değere (λ) ilişkin en iyi
tahminin hatası √λ olur.
Poisson
dağılımının
ortalama
değerinin
değişimi
ile
birlikte
değişen asimetriye dikkat
edilmelidir.
Üstel Dağılım
Üstel
değişim
gösteren
dağılımlar
için
kullanılmaktadır.
Poisson
dağılımı gösteren olayların
bir
sonrakinin
gerçekleşmesinin
dağılımı
için sıklıkla kullanılmaktadır.
Örneğin
bir
sonraki
radyoaktif bozunmaya kadar
geçen süre, bir sonraki
telefon aramanıza kadar
geçen süre vs.
Lorentz Dağılımı
Cauchy dağılımı olarak da
bilinmektedir. Daha çok fizikçilerin
kullandığı bir dağılımdır. Tayf
çizgilerindeki basınç genişlemesi
gibi homojen çizgi genişleme
mekanizmaları Lorentz dağılımı
göstermektedir.
Olasılık yoğunluğu fonksiyonunda
x0 konum parametresi ve γ ölçek
parametresidir (HWHM).
Sağ üstte görülen Lorentz
dağılımının
ölçek
parametre
değeri, 2γ = 2.354σ’dır.
Gamma Dağılımı
İki parametreli sürekli bir dağılım fonksiyonudur.
Üç farklı parametre ikilisiyle gösterimi yapılabilir:
1.
Şekil parametresi k ve ölçek parametresi θ
2.
Şekil parametresi α = k ve ters ölçek parametresi
β = 1/θ
3.
Şekil parametresi k ve ortalama parametresi μ =
k/ β
Doğrudan modelleme amacıyla bekleme sürelerinin
modellenmesi
temelinde,
yağmur
birikimi
modellerinde, sigortacılıkta, ölüme kadar geçen
bekleme süresinde, kablosuz iletişim sinyal
zayıflamasında vs. kullanılmaktadır.
Modelleme amacıyla kullanımda genellikle k ve θ
parametreleri, istatistiksel çıkarımda (özellikle Bayes
istatistiği) α ve β parametreleri ile gösterimi yaygındır.
Ki-Kare Dağılımı (Chi-Squared Dist.)
Serbestlik derecesi, k, kadar bağımsız standart normal
rastgele değişkenin toplamının dağılımıdır. Gamma
dağılımının özel bir halidir. Hipotez testi, güven aralığı
(confidence interval), uyum iyiliği (goodness of fit) gibi
bir çok istatistiksel çıkarımda kullanılmaktadır.
Doğal olayların modellenmesinde nadir olarak
kullanılmaktadır. Nadiren Helmert dağılımı olarak da
isimlendirilir.
Çoğu dağılım durumu merkezi limit teoremi gereği,
asimptotik olarak normal dağılıma yakınsar. Standart
normal dağılımın karesi basit bir ki-kare dağılımı
olduğu için, normal dağılımın kabul edildiği
durumlarda ki-kare dağılımı da kabul edilebilir.
Ki-kare olasılık yoğunluğu fonksiyonunda k, serbestlik
derecesidir!
Ki-Kare Dağılımı (Chi-Squared Dist.)
Test istatistiği parametresi olarak ki-kare değerleri
aşağıdaki şekilde hesaplanmaktadır.
Burada 𝜒 2 , Pearson test istatistiği parametresidir ve
asimptotik
olarak
bir
ki-kare
dağılımına
yaklaşmaktadır. Oi, i türünden yapılan gözlemlerin
değeri; Ei, aynı türden beklenen değerleri; n ise
toplam gözlem sayısını vermektedir.
Öğrencinin t Dağılımı (Student’s tdistribution)
Standart sapmanın bilinmediği bir normal dağılım
gösteren ana dağılımdan seçilen örnek bir dağılımın
ortalama değerinin dağılımıdır.
İki örnek dağılımın istatistiksel anlamlılık seviyesi
(statistikal significance) belirlemesinde kullanılan
Öğrencinin t dağılımı testinde, lineer regresyon
analizinde, iki örnek uzay ortalamaları farkının güven
aralığı (confidence interval) oluşturulmasında
kullanılmaktadır.
Normal bir dağılımdan alınan n elemanlı bir örnek
grubu alınması durumunda, n-1 serbestlik derecesine
sahip olan t-istatistiği aşağıdaki şekilde hesaplanabilir.
Öğrencinin t Dağılımı (Student’s tdistribution)
Yandaki görselde, serbestlik derecesinin değişmesi
ile t-dağılımının değişimi görülmektedir. Mavi ile
gösterilen eğri standart normal dağılımdır.
1 serbestlik derecesine sahip olan t-dağılımında
görüleceği üzere, t-dağılımı, daha geniş kanatlara
sahiptir. Bu normal dağılımın ortalama değerinden
daha uzakta ortalama değerlerin bulunma
olasılığının normal dağılıma göre daha fazla
olduğunu göstermektedir.
Serbestlik derecesi arttıkça ya da başka bir değişle
örnek elemanı sayısı arttıkça, t-dağılımı normal
dağılıma yakınsamaktadır.
Bunun sonucu olarak, örnek elemanı sayısının az
olması durumunda Öğrencinin t-dağılımının
kullanılması, normal dağılımın kullanılmasından
daha uygun olmaktadır.
F Dağılımı
F dağılımı, iki dağılımın karşılaştırılması temelindeki Ftestinde kullanılır. Aynı ana da iki örnek dağılımın
standart sapmasının karşılaştırılması ve bu şekilde güven
aralığı hesaplanmasında kullanılır. Örneğin bir olayın
modellenmesinde kullanılan iki farklı modelin güven
aralığının hesaplanması durumunda F-test kullanılabilir.
Bu test istatistikleri F dağılımına sahiptir.
Aşağıdaki X değerleri birer F istatistiğidir. Bu değerler F
dağılımı göstermektedir.
i)
Ui değerleri birer ki-kare dağılımı ve di değeleri bu
dağılımların serbestlik dereceleri,
ii)
𝑠𝑖2 değerleri normal birer sürecin kare toplam
değerlerinin serbestlik derecesin bölümü, 𝜎𝑖2 ise
ilgili normal süreçlerin standart sapmalarıdır.
Beta Dağılımı
Yüzde veya oran ile ifade edilebilen rastgele
olayların modellenmesi için kullanılan bir
dağılım fonksiyornudur. 0 ile 1 değerleri
arasında tanımlıdır. α ve β parametreleri
sıfırdan büyük değere sahip şekil
parametreleridir.
Dalga analizinde, proje yönetiminde, öznel
mantıkta modelleme dağılımı olarak
kullanılmaktadır. 0 ile 1 arasında tanımlı
olması,
Bayes
istatistiğinde
olasılılık
değerlerinin dağılımı olarak Bernoulli, binom
dağılımlarının öncül dağılımı (prior dist.)
şeklinde kullanılabilmesini sağlamaktadır.
Kaynaklar
• Measurements and their Uncertainties, Ifan G.
Hughes & Thomas P.A. Hase, Oxford University
Press, 2010
• Data Reduction and Error Analysis for the Physical
Sciences, Philip R. Bevington & D. Keith Robinson,
MC Graw Hill, 2003
• Görseller; www.stat.uiowa.edu/~mbognar/applets