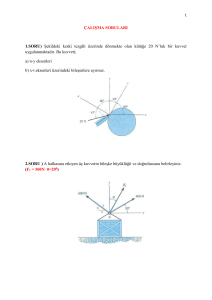
A.Ç
A.Ç
A.Ç
KUVVETİN ETKİLERİ
KUVVET NEDİR ?
Hareket eden bir cismi durduran,duran
bir cismi hareket ettiren,cisimlerin şekil ,
yön ve doğrultularını değiştiren etkiye
KUVVET denir.
A.Ç
KUVVETİN CİSİMLER ÜZERİNDE
ŞU ETKİLERİ VARDIR:
* Kuvvetin,cisimlerin hareket durumlarını
değiştirme etkisi vardır.
* Kuvvetin,cisimlerin şekil,biçim,yön ve
doğrultularını değiştirme etkisi vardır.
* Kuvvetin,cisimler üzerinde
döndürme etkisi vardır.
A.Ç
KUVVETİN ETKİLERİ
NOT I:
Kuvvetin sağlandığı kaynaklar
değişiktir; Örneğin kas kuvveti,yakıt
kuvveti, su buharı kuvveti, suyun ve
havanın kaldırma kuvveti
NOT II:
Kuvvet ile Ağırlık aynı
kavramlardır.
A.Ç
KUVVETİN GÖSTERİLMESİ
Fizikte temel anlamda iki
büyüklük vardır :
1. SKALER BÜYÜKLÜK
2. VEKTÖREL BÜYÜKLÜK
A.Ç
1. SKALER BÜYÜKLÜK
Sadece değeri ile belirtilen büyüklüktür.
Örnek; Kitabın boyu 160 cm dir.Karpuz
5 kg dır. 37 0C, 2g / cm3 vb.
Skaler büyüklükler normal matematik
kurallarına göre hesaplanır.
Sıcaklık,kütle,zaman,uzunluk,öz
kütle,enerji skaler büyüklüklerdir.
A.Ç
2. VEKTÖREL BÜYÜKLÜK
Yönü,doğrultusu ve değeri ile belirtilen
büyüklüklere VEKTÖREL BÜYÜKLÜK
denir.
Kuvvet,Hız,İvme gibi büyüklükler ,
yönlü büyüklüklerdir.
Kuvvet,vektörel büyüklük olduğundan
vektörle gösterilir.
A.Ç
VEKTÖR :
Yönlendirilmiş,sınırlandırılmış,
ölçülebilen doğru parçasıdır.
Vektör ( ) ile gösterilir.Ucundaki ok
işareti kuvvetin yönünü belirtir.
A.Ç
2. VEKTÖREL BÜYÜKLÜK
Örnek: F = 5 N ‘luk kuvveti
vektörle gösterelim;
1N = 1 cm
Uygulama noktası
F
C
A
Yön
Doğrultusu
B
Uzunluğu
1 cm uzunluk,1 N’u gösterecek şekilde
çizilmiştir.
F vektörü yada AB vektörü diye okunur.
A.Ç
KUVVETİN ELEMANLARI
Kuvvetin başlıca dört elemanı vardır ;
1. KUVVETİN YÖNÜ : Örnek şekilde
AB vektörünün ya da F vektörünün
yönü A dan B ‘ ye doğrudur.
2. KUVVETİN
DOĞRULTUSU
:
Şekildeki AB vektörünün doğrultusu
yere paralel ve C çizgisi üzerindedir.
A.Ç
3. KUVVETİN TATBİK VEYA
UYGULAMA NOKTASI :
AB vektörünün başlangıç noktası A
dır. Bitiş noktası ise B noktasıdır.
A.Ç
4. KUVVETİN ŞİDDETİ
( Değeri ) : Şekilde 1 cm ‘lik uzunluk
1N olarak gösterilirse F vektörünün
şiddeti ( değeri ) 5N olur.
A.Ç
Örnek
1.Ayşe masayı 5N’luk kuvvet ile doğu batı
doğrultusunda doğu yönüne çekti (Yönü)
2. Ayşe masayı 5N ‘luk kuvvet ile doğu batı
doğrultusunda doğu yönünde C noktasında
çekti ( doğrultusu )
3. Ayşe masayı 5N ‘luk kuvvet ile doğu-batı
doğrultusunda çekti ( uygulama nokt.)
4. Ayşe masayı 5N ‘luk kuvvetle çekti
( şiddeti )
A.Ç
KUVVETİN ÖLÇÜLMESİ
Kuvveti veya ağırlığı ölçmek için
DİNAMOMETRE ler veya Yaylı el
kantarları kullanılır.Dinamometreler,
kuvvet ölçen araçlardır ve cisimlerin
esneklik özelliğinden faydalanılarak
yapılmışlardır.
A.Ç
KUVVET BİRİMLERİ
1. Kilogram - kuvvet ( kgf ) : 1 kg kütleye Paris’te
etki eden yerçekimi kuvvetine 1 kgf denir.
1 kgf = 9.8 N
2. Newton ( N ) : 1 kgf ‘ in 9,8 de birine 1 N denir.
9,8 N = 1 kgf eder.
A.Ç
KUVVET BİRİMLERİ
3. Gram-kuvvet ( gf ) : 1 kgf ‘in 0.001 ‘e 1 gf
denir. 1gf = 0.001 kgf 1kgf = 1000gf
4. Dyne ( dyn ) : 1 gf ‘in 980 de birine 1 dyn
denir. 1gf = 980 dyn 1N = 100000 dyn
A.Ç
Örnek: : 3 kgf kaç Newton eder?
1 kgf
9.8 N ederse
3 kgf
X N eder.
X = 3 . 9.8
X = 29.4 N eder.
A.Ç
BİLEŞEN KUVVET
Aynı noktaya uygulanan iki ya da daha çok
kuvvetler.
F1
F2
F1
F2
A.Ç
KUVVETLERİN BİLEŞKESİ
( Bileşke Kuvvet )
Bir cisme aynı anda uygulanan iki veya daha
çok kuvvetin yerini tutan tek kuvvete,
BİLEŞKE KUVVET denir. R ile gösterilir.
A.Ç
BİLEŞKE KUVVET
F2
F1
Bileşke kuvvet
R ( bileşke kuvvet )
R = F1 + F2
R = 2 birim + 3 birim
R = 5 birim
olur.
A.Ç
BİR NOKTAYA ETKİ EDEN AYNI
DOĞRULTULU VE AYNI YÖNLÜ
KUVVETLERİN BİLEŞKESİ
Aynı doğrultuda ve aynı yönde iki kuvvetin bileşkesi bu
kuvvetlerin doğrultusu ve yönündedir.Değeri kuvvetlerin
şiddetlerinin toplamına eşittir.
F1
O
F1
F2
F2
R
R = F1 + F2
A.Ç
Örnek : Doğrultuları ve yönleri aynı
2 N ve 3 N ‘luk iki kuvvetin bileşke
şiddeti ne kadardır?
F1 = 2 N
F2 = 3 N
R= ?
R = F1 + F2
R =2 N + 3 N
R= 5N
olur.
A.Ç
DOĞRULTULARI AYNI YÖNLERİ ZIT
İKİ KUVVETİN BİLEŞKESİ
Doğrultuları aynı,yönleri zıt iki kuvvetin
bileşkesini hesaplamak için şiddeti büyük
olan kuvvetten şiddeti küçük olan kuvvet
çıkarılır.
Bileşke kuvvetin uygulama noktası O
noktasıdır.Doğrultusu F1 ve F2
doğrultusundadır. Yönü F2 yönündedir.
A.Ç
DOĞRULTULARI AYNI YÖNLERİ ZIT İKİ
KUVVETİN BİLEŞKESİ
F1
F2
F1
F2
O
R
R = F2 - F1
A.Ç
Örnek : Doğrultuları aynı,yönleri zıt
2 N ve 3 N ‘luk iki kuvvetin bileşke
şiddeti ne kadardır?
F1 = 2 N
R = F2 - F1
F2 = 3 N
R=3 -2
R= ?
R = 1 N olur.
A.Ç
KESİŞEN KUVVETLER
*İki ya da daha çok kuvvetin etkisinde
olan cisimler,daima bileşke kuvvetin
yönünde ve doğrultusunda hareket
ederler.
Bir noktaya uygulanan doğrultuları
farklı iki kuvvete Kesişen Kuvvet
denir.
A.Ç
Kesişen kuvvetlerin bileşkesinin
bulunmasında iki metot kullanılır:
A.Ç
1. UÇ UCA EKLEME METODU
Kuvvetler,doğrultu,yön ve şiddeti
değiştirilmeden yani paralel kalacak
şekilde,sıra gözetmeksizin uç uca eklenir.
İlk kuvvetin başlangıç noktasını,son
kuvvetin bitiş noktasına birleştiren kuvvet
Bileşke kuvvettir.Burada sıranın önemi
olmayıp istenilen kuvvetten
başlanıp,istenilenden devam edilebilir.
A.Ç
Örnek : Şekilde verilen iki kuvvetin bileşkesini bulunuz.
F1
Çözüm :
F2
F2
1. İşlem: F1 kuvvetinin doğrultu,yön ve şiddeti
değiştirilmeden herhangi bir noktaya taşınır.
F1
2. İşlem : F2 kuvveti yine doğrultu,yön ve
şiddeti değiştirilmeden F1 in ucuna ilave taşınır.
F2
3. Son işlem :İlk vektörün başlangıcını ( A ),son vektörün bitimine ( B ),
birleştiren R vektörü bileşkeyi verir.
B
F1
R
R = F 1 + F2
A
F2
A.Ç
Örnek: Şekilde verilen üç kuvvetin
bileşkesini bulunuz.
F1
F2
F3
Çözüm :
1. İşlem
F2
F3
2. İşlem
F3
F1
F2
3. İşlem
F3
F1
R
F2
4.İşlem
R =F1 + F2 + F3
F3
A.Ç
2. PARALEL KENAR METODU
I. İki Kuvvetin Bileşkesi :
Bir noktada kesişen,doğrultuları farklı iki kuvvetin bileşkesi paralel kenar kuralı
ile bulunur.İki kuvvetin başlangıç noktası bir noktaya taşınır.Meydana gelen şekil
paralel kenara tamamlanır.Başlangıç noktasından geçen köşegen bileşke kuvveti
verir.
F1
F1
R
F2
F2
R =F1 + F2
Kuvvetler arasındaki açı ise bileşke kuvvetin büyüklüğü ;
Cos teoremi
2
2
2 -
R = F1 + F2 + 2 F1.F2.cos
İfadesi ile bulunur.
Aradaki + - işareti < 90 ise ( + ), > 90 ise ( - ) alınır.
A.Ç
Örnek : 60N ve 80N ‘luk iki kuvvetin aralarındaki açı
a ) 600
bulunuz.
b ) 900
c ) 1200 olduğuna göre bileşkelerini çizimle
Çözüm : Kuvvetleri vektörle gösterebilmek için önce bir ölçek seçilir.
60 ve 80 sayıları 20 nin katlarıdır. Onun için;
a)
c)
F1 = 60 N = 3 birim = 3 cm, F2 = 80 N = 4 birim = 4 cm vektörle gösterilir.
F1
A
0
=60
F1 =3cm
R
F2 =4cm
600
R=?
OA = 6.1 birim
O
R = 6.1.20
F2
R = 122 N
=1200
F1
R
F1 =3 cm
R = 3.6 birim
F2 =4cm
R =3.6.20
R = 72 N
R=?
1200
F2
A.Ç
b ) = 900
F1 =3 cm
F2 =4 cm
A
F1
R
R=?
F2
O
= 900 olduğu için bileşkenin şiddeti Pisagor Bağıntısı ile hesaplanır.
F1 = 60 N
F2 = 80 N
=900
R=?
2
2
2
R = F 1 + F2
2
2
2
R = ( 60 ) + ( 80 )
2
R = 3600 + 6400
2
R = 10000
R = 100 N
olur.
A.Ç
Aynı doğrultuda ve zıt yönde iki kuvvet aynı bir
noktaya uygulanırsa ve bu kuvvetler birbirine
eşit olursa bileşkenin değeri sıfır olur.Bu kuvvetlere
DENGELEYEN KUVVETLER denir.
F2 =2N
F1 =2N
R = F2 - F1
R = 2N - 2N
R =0
A.Ç
Bir cisme etki eden kuvvetlerin bileşkesi
sıfır ise ( R = 0 ) o cisim dengededir.
Bileşke kuvvet sıfır değilse,cismi
dengelemek için,bileşkenin uygulandığı
noktaya bileşkeye zıt yönde ve eşit
şiddette kuvvet uygulanmalıdır.
A.Ç
R=
RI
F1
R
R = F1 + F2
Bileşke kuvvet
Dengeleyici RI
kuvvet
Cisim
F2
Bileşke kuvvetin yaptığı etkiyi tek başına
karşılayan kuvvete DENGELEYİCİ
KUVVET denir.
A.Ç
Bileşke kuvvetin yaptığı etkiyi tek
başına karşılayan kuvvete
DENGELEYİCİ KUVVET denir.
DENGELEYİCİ KUVVET
* Bileşkeye eşit şiddette
* Bileşke ile aynı doğrultuda
* Bileşke ile zıt yöndedir.
A.Ç
Örnek : Şekildeki cisme F1, F2 ve F3 kuvvetleri
etki etmektedir.Cismi durdurmak için hangi
yönde ve nekadarlık bir kuvvet uygulanmalıdır?
F1 = 3N
F2 =2N
F3=6N
Çözüm :Bileşkeye eşit ve zıt yönlü kuvvet dengeleyici kuvvettir.Önce bileşke
bulunur;
FX = 6 - 2
FX = 4N olur.
FY=3N
R
Pisagor bağıntısından;
R2 = Fx2 + Fy2
2N
6N
FX=4
N
RI
R2 = 42 + 3 2
R2 = 25
R = 5N
RI = R = 5N
bulunur.
A.Ç
DENGENİN ÖZEL HALLERİ
1. Kesişen üç kuvvet dengede ise,herhangi iki kuvvetin bileşkesi ters yöndeki
üçüncü kuvvete eşit şiddettedir.
F2
Şekilde,üç kuvvet dengededir.
F1
Buna göre ;
F3
F2
A ) Şekildeki F1 ile F2 nin bileşkesi F3 e
eşit ve zıt yöndedir.
F1
B ) F2 ile F3 ün bileşkesi F1 e
eşit ve zıt yöndedir.
F2
F1
F3
F3
C ) F1 ile F3 ün bileşkesi de F2 ye eşit ve zıt
yöndedir.
F2
F1
F3
A.Ç
2. Kesişen üç kuvvet dengede ve aralarındaki açı 120 şer derece ise
bu üç kuvvet birbirine eşittir.
F1
1200
F3
1200
1200
F2
F1 = F2 = F3
Veya kesişen üç eşit kuvvetin aralarındaki açılar 120 şer derece ise
bu sistem dengededir.
A.Ç
Örnek : A noktasına etkiyen F1,F2 ve
F3 kuvvetlerinin bileşkesi hangi yönde
ve kaç N şiddetindedir?
F2=30N
F3 =40N
600
A
Çözüm :F1 ve F2 kuvvetleri birbirine eşit ve aralarındaki açı
1200 lik açı olduğundan bileşkesi M yönünde ve 30N
şiddetinde olur.F3ile M yönündeki 30 N luk kuvvet ters
yönlü olduklarından; R = 40 - 30 = 10 N olur.
O halde bileşke 10 N şiddetinde ve F3 yönündedir.
M
600
F1=30N
F1 = 30 N
F3 = 40 N
30 N
F2 = 30 N
A.Ç
3. Kesişen üç kuvvet dengede ise küçük açının karşısındaki kuvvet büyük,büyük
açının karşısındaki kuvvet küçüktür.
F1
F2
800
1500
1300
F3
En küçük açı 800 nin karşısındaki kuvvet olan F3 en büyük,en büyük açı
1500 nin karşısındaki F2 en küçüktür.
A.Ç
Örnek : Şekildeki sistem dengededir.İpteki
T1 , T2 ve P gerilme kuvvetleri arasında
nasıl bir bağıntı vardır?
370
T2
T1
P
Çözüm : Kesişen üç kuvvet dengede ve
kuvvetler arasındaki açı ise 900,1270 ve
1430 dir. En küçük açının karşısındaki P
kuvveti en büyük,en büyük açı ( 1430 ) nın
karşısındaki
T1 kuvveti en küçüktür.
O halde ; P >T2 > T1 dir.
370
530
T1
T2
370
1270
530
1430
P
A.Ç
4. Bir cisme birden fazla kuvvet etki ediyor ve bu kuvvetler grubunda da
doğrultuları aynı olan kuvvetler varsa; bileşkeyi bulurken,doğrultuları aynı
olan kuvvetlerden başlamak ve devam etmek işlem kolaylığı sağlar.
4f
Örnek :Şekilde M cismine etki eden
kuvvetlerin bileşkesini bulunuz?
M
600
2f
600
f
3f
Çözüm :
3f
1. İşlem :Şekildeki 4 f ile f
kuvveti doğrultuları aynı ancak
zıt yönlüdür.Bu ikisinin bileşkesi
4 f yönünde ve 3 f şiddetindedir.
2f
M
600
600
3f
A.Ç
2. İşlem : 3 f şiddetinde iki kuvvet ve aralarındaki açı 1200
olduğundan bileşke, açı açıortay üzerinde ve 3 f kadardır.
2f
3f
3. İşlem : 3 f ve 2 f şiddetindeki iki kuvvet,doğrultuları aynı ancak zıt
yönlü iki kuvvetin bileşkesi 3 f yönünde ve f şiddetindedir.
f
A.Ç
PARALEL KUVVETLERİN BİLEŞKESİ
I. Paralel ve Aynı Yönlü İki Kuvvetin Bileşkesi :
Ağırlığı önemsenmeyen AB çubuğunun iki ucuna şekildeki gibi F1 ve F2
kuvvetleri etki etmektedir.Bileşke kuvvetler arasında ve büyük kuvvete
daha yakındır. Bileşkenin yeri : F1 . X = F2 .x den bulunur.
Ya da F1. AC = F2. BC bağıntısıyla bulunur.
A
C
x
B
y
F2
F1
R = F 1 + F2
F1 x AC = F2 x BC
A.Ç
Örnek : 50 cm uzunluğundaki bir çubuğun uçlarına iki cisim asılıyor. Biri
10 gf ağırlığında ve bileşkeden 30 cm uzaklıkta olduğuna göre ikinci cismin
ağırlığını bulunuz?
50 cm
Çözüm :
O
A
B
20cm
30 cm
F1 = 10gf
F2= ?
F1 . AO = F2 . BO
R
10 . 30 = F2 . 20
F2 = 15 gf bulunur.
A.Ç
II. PARALEL VE ZIT YÖNLÜ İKİ KUVVETİN BİLEŞKESİ
Ağırlığı önemsenmeyen AB çubuğuna F1 ve F2 kuvvetleri paralel ve zıt yönlü
uygulanmış ise,bileşke,büyük kuvvetin dışında ve büyük kuvvetin yönündedir.
Bileşkenin yeri :
F1 . x = F2 .y
İfadesiyle bulunur.
Paralel kuvvetlerin bileşkesinin uygulama noktası demek,çubuğun dengede
kalabilmesi için konulacak desteğin yeri veya ipin asıldığı nokta demektir
F2
y
O
A
B
x
F1 . AO = F2 . AB
R = F 1 + F2
F1
A.Ç
A.Ç
Bir cismin hareketine,bulunduğu yüzey etki
eder.Yüzeyin kaygan veya pürüzlü olması hareketi
kolaylaştırır ya da zorlaştırır.
Cisim
Yatay bir düzlemde herhangi bir cismi belli
hızlarla atarsak cisim mutlaka yavaşlayarak
durur.Bazı cisimler daha çabuk dururken bazı
cisimler de daha uzun süre sonra durur.
A.Ç
Acaba cisimlerin durmasının
nedeni nedir?
Yavaşlayarak duran bir cisme hareket yönüne
ters yönde bir kuvvet uygulanmaktadır.
İşte cisim ile zemin arasındaki bu kuvvete
SÜRTÜNME KUVVETİ denir.
A.Ç
Yada duran cismi harekete başlatmaya
yetecek olan kuvvete değerce eşit,aynı
doğrultulu ve zıt yönlü kuvvete
SÜRTÜNME KUVVETİ denir.
FS
F
Fs = Sürtünme kuvveti
A.Ç
SÜRTÜNME KUVVETİNİN
ÖZELLİKLERİ
* Sürtünme kuvvetinin büyüklüğü,
sürtünen yüzeye dik olan tepki kuvvetiyle
( cismin ağırlığı ) doğru orantılıdır.
* Sürtünme kuvveti,sürtünen yüzeylerin
cinsine bağlıdır.Bu kuvvet,cilalı
yüzeylerde çok az,pürüzlü yüzeylerde
çok büyüktür.
A.Ç
* Sürtünme kuvveti,sürtünen yüzeylerin
alanına bağlı değildir.
* Cismin ağırlığı arttıkça sürtünme
kuvveti de aynı oranda artar.
* Sürtünme kuvveti daima harekete
zıt yöndedir.
A.Ç
* Hareket ettirici etkisi yoktur.Hareketi
engelleyici etkisi vardır.
* Uygulanan kuvvet sürtünme kuvvetine eşit
ise net kuvvet sıfır olur.İlk hız varsa cisim
sabit hızla hareket yapar,duruyorsa
durgunluğunu sürdürür.
* Sürtünmeli bir yüzeyde duran bir cismin
harekete geçebilmesi için uygulanan
kuvvetin sürtünme kuvvetinden büyük
olması gerekir. ( F > FS )
A.Ç
N
SÜRTÜNME KUVVETİ
V
FS
G = m.g
FS = k.N
FS = Sürtünme kuvveti
k = Cisim ile yüzey arasındaki sürtünme katsayısıdır.
Bu katsayı cisim ile zeminin özelliğine bağlıdır.Kaygan
yüzeyler için daha küçüktür.
N = Zeminin cisme gösterdiği tepki kuvvetidir.
Tepki kuvveti yüzeye daima diktir.
G = Cismin ağırlığı
A.Ç
Yatay zeminde duran bir cisim için tepki
kuvvet ( N ) cismin ağırlığına eşittir.
N
G
N=G
Cismin üzerine bir F kuvveti
uygulanırsa tepki kuvveti;
N F
G
N=F+G
NOT : Sürtünme kuvveti
olmasaydı acaba ne olurdu ?
1. Yürüyemezdik,yürüsek bile tekrar
duramazdık.
2. Uçaklar inip kalkamazdı.
3. Yağmur damlaları mermi gibi
kafamıza inerdi.
4. Duvara çivi çakamazdık.
KISACA HAYAT YAŞANMAZ HALE
GELİRDİ.
A.Ç
A.Ç
Bir cismin,seçilen bir noktaya göre zamanla yer
değiştirmesine HAREKET denir.
Hareketli ve Hareketsiz Cisimler
A
O
d :Uzaklık ( yol )
O , noktası başlangıç noktasıdır.
d = A cisminin aldığı yol
A.Ç
Bir doğru üzerinde bulunan A cismin sabit
bir O noktasına göre,d uzaklığı zamanla
değişiyorsa A cismi hareket ediyor denir.
A cisminin O noktasına göre d uzaklığı değişmiyorsa,
cismi hareketsizdir.
A
Hareket halindeki bir trende insan,trene göre
hareketsiz,yere göre hareketlidir. Tren içinde gezinen insan
ise,trene göre hareketlidir.
Yol kenarında sizi izleyen bir kişiye göre,trende otursanız
da trende gezinseniz de hareketlisinizdir.
A.Ç
KONUM VE YER
DEĞİŞTİRME
KONUM NEDİR ?
Konum,bir kimsenin ya da bir şeyin
bir yerdeki durumu veya duruş
biçimi (vaziyet )
A.Ç
Hareketin incelenmesinde ilk basamak,
hareket eden cismin konumunu tespit
etmektir. Konumu tespit etmek için belirli
bir noktayı seçmek gerekir.Seçilen bu
noktaya başlangıç noktası denir.
İşte hareketlinin konumu,başlangıç
noktasına olan uzaklığı ile belirlenir.Bu
ise vektörel büyüklüktür.
A.Ç
KONUM VE YER DEĞİŞTİRME
Son konum
A
İlk konum
B
Yer değiştirme
C
A.Ç
Bir cismin konumu;sabit kabul edilen
noktadan cismin bulunduğu nokta arasındaki
uzaklıktır.Şekilde adamın ağaca göre konumu
AB ( AB vektörü ) dür.Son konumu AC (AC
vektörü ) ile gösterilir.
Vektörlerin uzunluğu adamın ağaca uzaklığını
belirtir.AC vektörü,AB vektöründen büyük
olduğundan adamın ağaçtan uzaklaştığı sonucuna
varırız.
A.Ç
Yer Değiştirme ise ; Cismin ilk bulunduğu
noktadan son bulunduğu noktaya çizilen
vektör ile belirlenir.
Yer değiştirme miktarı ise son konumu
belirten vektörün uzunluğundan ilk konu
belirten vektörün uzunluğu çıkarılarak
bulunur.
YER DEĞİŞTİRME = SON KONUM - İLK KONUM
A.Ç
Örnek : Yukarıdaki şekilde,vektörlerin
uzunlukları AC =24 m, AB = 10 m ise yer
değiştirme miktarını bulunuz ?
AC = 24 m
AB = 10 m
BC = ?
BC =
AC
- AB
BC = 24 m - 10 m
BC = 10 m
olur.
1. Yer değiştirme artı ( + ) çıktığından,adam başlangıç
noktasından uzaklaşmıştır.
2. Yer değiştirme eksi ( - ) olması durumunda cismin
başlangıç noktasına yaklaşması demektir.
A.Ç
Örnek :
Batı
Doğu
K
L
M
N
P
R
S
T
100
50
0
50
100
150
200
250
Yukarıdaki doğru üzerinde bulunan noktalar 50 m aralıklı sıralanmıştır. M
noktası ise başlangıç noktası olarak seçilmiştir. Buna göre ;
A ) Bir araba M noktasından ( başlangıç noktası ) P noktasına kadar gidiyor.
.Arabanın M noktasına göre konumunu söyleyiniz ?
B ) K noktasının M noktasına göre konumu nedir ?
A)
Konum = MN
+ NP
B)
Konum = ML + KL
Konum = 50 m + 50 m
Konum = 50 m + 50 m
Konum = 100 m ( + ) DOĞU olur.
Konum =100 m
K noktasının M noktasına
göre konumu ; - 100 m Batı
A.Ç
EK BİLGİ
A.Ç
EVRENDE HER ŞEY
HAREKETLİDİR
Bir cismin sabit kabul edilen bir noktaya
göre zamanla yer değiştirmesine hareket denir.
Çevremizdeki evler, ağaçlar ve dağlar
hareketsizdir. Hareket halinde bulunan bir
trende, yanınızda oturan yolcuya göre
hareketsiz, yol kenarındaki duran kişilere
göre hareketli sayılırsınız.
A.Ç
Bir cismin bulunduğu yere konum
denir.
Cismin harekete başladığı
konuma ilk konum, hareket
sonunda ulaştığı konuma ise son
konum denir. Son konum ile ilk
konum arasındaki uzaklığa ise yer
değiştirme denir.
A.Ç
Yer Değiştirme = Son Konum – İlk Konum
Yol (km)
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
Şekildeki otomobil 2. kilometreden 9. kilometreye gitmiştir.
A.Ç
Yer değiştirme X = Xson – Xilk
X = 9 – 2 = 7 km.
Yönü sağa doğrudur. Yer değiştirme
vektörel bir büyüklüktür.
A.Ç
FİZİKTE İKİ TÜR BÜYÜKLÜK VARDIR
Skaler büyüklük
Skaler büyüklük:
Sayısal bir değer ve
bir birimle ifade
edilebilen
büyüklüklere skaler
büyüklük denir.
Kütle, uzunluk ve
hacim skaler
büyüklüklerdir.
Örn: 5 metre, 10
litre, 6 kilogram
Vektörel büyüklük
Vektörel büyüklük:
Yönlü doğru parçalarına
vektör denir. Şiddeti, yönü,
doğrultusu ve uygulama
noktası belli olan
büyüklüklere vektörel
büyüklük denir. Örneğin hız,
yer değiştirme, ağırlık ve
kuvvet vektörel
büyüklüklerdir.
A.Ç
Vektörel büyüklük
U
y
g
u
l
a
m
a
n
o
k
t
a
s
ı
A
f
u
z
u
n
l
u
ğ
u
Y
ö
n
d
D
o
ğ
r
u
l
t
u
B
Not: Yol skaler, yer değiştirme vektörel bir büyüklüktür.
A.Ç
Örnek: Çocuk A noktasından önce B noktasına sonra
C noktasına hareket ediyor. Çocuğun yer değiştirme
vektörünü çiziniz.
B
B
C
C
X
A
A
A.Ç
Hareket eden cisimler zamanla yer değiştirirler.Birim
zamanda yapılan yer değiştirmeye HIZ adı verilir.
HIZIN HESAPLANMASI
Bir hareketlinin hızı,yer değiştirme miktarının,
yer değiştirme süresine bölünmesi ile bulunur;
Hız =
Yer değiştirme miktarı
Yer değiştirme süresi
HIZ =
YOL
ZAMAN
A.Ç
Yol = metre ( m ) ,zaman= saniye ( s )
olarak alınırsa;
YOL ( m )
HIZ =
( m/s)
ZAMAN ( s )
YOL = HIZ x ZAMAN
ZAMAN =
YOL
HIZ
Olur.
A.Ç
X = Yer değiştirme
t = zaman
X
V =
t
V = Hız
t1 ve t2 zaman aralığında yer
değiştirme miktarı: X2 - X1 is ;
V=
X 2 - X1
t 2 - t1
=
X
t
Olur.
A.Ç
Örnek : Bir araba 160 metrelik yolu 20 saniyede
alıyor.Arabanın hızını bulunuz?
Yol = 160 m
Hız =
Zaman = 20 s
Hız = ?
Hız =
Yol
Zaman
160 m
20 s
Hız = 8 m / s
A.Ç
Soru 1 : Bir cisim 8 m / s ‘lik sabit hızla 30
saniye hareket ediyor. Cismin aldığı yolu
bulunuz ?
Soru 2 : Malatya ile Ankara arası 600 km
dir. Malatya’dan Ankara’ya giden yolcu
otobüsü bu yolu 8 saatte alıyor.Otobüsün
hızını bulunuz.
A.Ç
Soru 3 : Bir araba doğudan batıya
doğru 72 km / saat hızla 0.2 saat
hareket ediyor.Araba kaç metre yer
değiştirmiştir?
A ) 14.4
B ) 144
C ) 1440
D ) 14400
A.Ç
ORTALAMA HIZ
Değişken hıza sahip olan bir hareketlinin,yol
boyunca yapmış olduğu değişik hızların
ortalamasına ORTALAMA HIZ denir.
Örnek :
60 km
50 km
90 km
O
C
30 dakika
A 1 saat
B 30 dakika
Bir otomobil,gideceği yolun 50 km’sini 30 dakikada,
90 km’sini 1 saatte,60 km ‘sini de 30 dakikada
almıştır.Otomobilin yol boyunca ortalama hızını
bulunuz.
A.Ç
X1 =50 km
X2 = 90 km
X3 = 60 km
XT = ?
XT = X1 + X 2 + X3
XT = 50+90+60
XT =200 km
A.Ç
t1 = 1 /2 saat
t T = t 1 + t 2 + t3
t2 = 1 saat
t T = 1 /2 + 1 + 1 / 2
t3 = 1 / 2 saat
t T = 2 saat
tt = ?
VORT. =
XT
tT
200
VORT. =
2
VORT. = 200 km / h
A.Ç
A.Ç
A.Ç
A.Ç
A.Ç
A.Ç
İŞ NEDİR?
Bir kuvvet,bir cisme uygulandığında,onu
kendi doğrultusunda hareket ettiriyorsa,
fen anlamında bu kuvvet bir iş yapmıştır.
A.Ç
İŞ NEDİR?
Bu tanımdan da anlaşıldığı üzere fen
anlamında bir iş yapılabilmesi için şunların
gerçekleşmesi gerekir;
1. Bir cisme bir kuvvetin uygulanması
gerekir,yani bir kuvvet olmalıdır.
2. Bu kuvvet o cisme bir yol aldırması
gerekir.
3. Kuvvetle yolun aynı doğrultuda olması
gerekir.
A.Ç
İŞ NEDİR?
Kuvvet : F
Yol
:X
İş
: W
F ( Kuvvet )
X ( Yol )
İŞ = KUVVET x YER DEĞİŞTİRME
İŞ = KUVVET x YOL
W = F . X
A.Ç
İŞ BİRİMLERİ
İ Ş = Kuvvet x yol olduğundan iş
birimleri de kuvvet birimi ile yol
( uzunluk )
biriminin çarpımına
eşittir.
A.Ç
İŞ BİRİMLERİ
Kuvvet
( F)
Yol
(X)
N
dyn
m
cm
kgf
m
1 jul = 107 erg
İş = Kuvvet x Yol
W=F.X
Jul
Erg
kgf.m
1 kgm = 9.8 jul
A.Ç
Örnek : Bir arabaya yatay yolda 2 kgf’ lik
yatay bir kuvvetle 5 metre yol aldırıldığında
yapılan iş ne olur?
F = kgf
X =5m
W =?
W = F. X
W = 2 kgf .5 m
W = 10 kgm
olur.
A.Ç
Örnek :Ağırlığı 3 kgf olan bir çanta 150 cm
yüksekliğindeki rafa kaldırılıyor.Buna göre
yapılan işi bulunuz?
Çantayı rafa kaldırmakla yerçekimi
kuvvetine karşı iş yapılmıştır.
Yükseklik ( yol )
( h ) = 150 cm = 1.5 m
Ağırlık ( kuvvet )
( G ) = 3 kgf
İş
(W)
W=G.h
W = 3 kgf . 1.5 m
W = 4.5 kgm olur.
1 kgm = 9.8 jul
= ?
4.5 kgm = 44.1 jul olur.
A.Ç
Örnek : 300.000 jul’lük iş yapmak için
60 N ‘luk kuvvet uygulanıyor.
Cisim ne kadar yol alır?
A.Ç
Örnek : Duran bir arabayı,sabit
kuvvetle ve kuvvet yönünde 20 m iten
bir kişinin 3528 jul’lük iş yapması
için kaç Newton’luk kuvvet
uygulanması gerekir?
A ) 10.2
B ) 18
C ) 176.4
D ) 196
A.Ç
A.Ç
A.Ç
ENERJİ ÇEVRİMLERİ
Çevremize baktığımızda ( biz görelim ya
da görmeyelim) bir takım hareketlerin
olduğunu söyleyebiliriz.Otomobiller
hareket eder,insanlar hareket
eder,iletken tel içerisinde elektronlar
hareket eder.
A.Ç
Bütün bu olaylar sırasında bir takım
enerjiler başka enerjilere çevrilir.
Örneğin; Benzinin kimyasal enerjisi ;
Otomobilin karbüratörü içerisinde hava
ile karıştırılarak bujilerle de ateşlenerek
pistonun hareket etmesini sağlar.Bu
hareket tekerleklere aktarılarak
otomobile Kinetik Enerji kazandırır.
A.Ç
Barajda birikmiş suda Potansiyel
Enerji bulunur,bu su yüksek bir yerden
akıtılarak Kinetik Enerji elde edilir.
Pervaneye çarpan su pervaneyi
döndürür, Mekanik Enerjiye dönüşür.
Pervaneye bağlı dinamo elektrik
enerjisi üretir. Üretilen elektrik enerjisi
ile ampul ışık verir ışık enerjisine,ütü
ısınır ısı enerjisine dönüşür.
A.Ç
Fiziğin en temel yasalarından birisi
ENERJİNİN KORUNUM YASASI dir.
Fiziksel ve kimyasal olaylarda enerji bir
şekilden başka bir şekle dönüşür.
A.Ç
Örnek I: Yediğimiz besinlerin
vücuttaki değişimini enerji dönüşümü
ile nasıl açıklarsınız ?
Çözüm : Besinlerin yapısındaki
kimyasal enerji hücrelerde yakılarak
ısı enerjisi ve hareket enerjisi olarak
kullanılır.
A.Ç
Örnek II : Termik santrallerde kömür
yakıt olarak kullanılır ve elektrik
üretilir.Bu işlemde enerji dönüşümü
nasıldır ?
Çözüm : Kömürdeki kimyasal enerji ısı
enerjisine dönüşür,suyu buharlaştırır.
Buharın hareket enerjisi türbinlerde
hareket enerjisine, dinamo elektrik
enerjisi üretir.Elektrik enerjisi,ısı,ışık vb.
ısı enerjisine dönüşür.
A.Ç
Bir cismin ya da sistemin iş yapabilme
yeteneğine ENERJİ denir.
ENERJİ ÇEŞİTLERİ
Isı enerjisi,ışık enerjisi,kimyasal enerji,
güneş enerjisi,elektrik enerjisi,buhar
enerjisi,rüzgar enerjisi,nükleer enerji ve
Mekanik enerji vb.
A.Ç
BİZ MEKANİK ENERJİYİ
İNCELEYECEĞİZ
MEKANİK ENERJİ İKİ KISIMDIR;
1 . KİNETİK ENERJİ
( Hareket enerjisi )
2. POTANSİYEL ENERJİ
( Durum enerjisi )
A.Ç
KİNETİK ENERJİ
( Hareket Enerjisi )
Hareket halindeki cisimlerin hızları
sebebiyle sahip oldukları enerjiye
KİNETİK ENERJİ denir.
Yada bir cismin hareketinden( hızından )
dolayı sahip olduğu enerjiye Kinetik Enerji
adı verilir.
Kinetik enerji,hareket eden cismin
kütlesi ve hızıyla artar.
A.Ç
KİNETİK ENERJİ
( Hareket Enerjisi )
Kinetik enerji ( jul )
: Ek
Cismin kütlesi ( kg )
: m
Cismin hızı ( m/s )
:V
1
Ek =
2
mv2
A.Ç
Örnek : 5 g kütleli bir mermi 500 m/s ‘lik
bir hızla ateşleniyor.
Merminin ateşlendikten sonra kinetik
enerjisi kaç jul ‘ dür?
A ) 100
B ) 250
C ) 500
D ) 625
A.Ç
ÇÖZÜM:
m = 5 g = 0.005 kg
1
v = 500 m / s
Ek =
Ek = ?
1
Ek =
Ek =
2
m v2
0.005 . ( 500 )2
2
0.005.25000
2
Ek = 625 jul
A.Ç
Örnek : 4 kg kütleli bir cismin hızı 5 m / s
olduğuna göre;sahip olduğu kinetik enerji
kaç jul ‘dür?
A ) 100
B ) 20
C ) 25
D ) 50
A.Ç
Örnek : Kütlesi 5 kg olan bir cisim yere
1800 jul’lük enerji ile çarptığına göre;
cisim kaç metre yüksekliğinde serbest
bırakılmıştır? ( g = 10 N / kg )
A ) 3.6
B ) 1.8
C ) 36
D ) 18
A.Ç
Bir cismin veya sistemdeki depo edilmiş ve
istenildiği zaman kullanılabilen enerjiye
POTANSİYEL ENERJİ denir.
Örnek: Depolanmış su buharının,
sıkıştırılmış bir yayın,yüksekte duran
cismin,barajda toplanan suyun,sıkışan
havanın Potansiyel Enerjisi vardır.
A.Ç
POTANSİYEL ENERJİ
masa
h = Yükseklik
Yer
A.Ç
Belirtilen bir yere göre G = m.g ağırlığındaki bir cismin
potansiyel enerjisi;
POTANSİYEL ENERJİ = AĞIRLIK x YÜKSEKLİK
EP = G.h
Potansiyel enerji =EP
Ağırlık
:G
jul
Yükseklik
Newton
metre
:h
Yer çekim ivmesi = g
G = m.g
olduğundan ;
EP =
m.g.h
A.Ç
NOT . Yukarıdaki şekle göre masanın
üzerinde duran bir cismin masaya göre h
yüksekliği olmadığından Potansiyel
enerjisi sıfırdır.Fakat aynı cismin yere
göre h yüksekliği olduğu için bir
Potansiyel enerjisi vardır.
A.Ç
Örnek : 20 metre yüksekte duran 8 kg’lık bir
kayanın potansiyel enerjisini bulunuz? ( g
= 9.8 N / kg )
h = 20 m
m = 8 kg
EP = m.g.h
g = 9.8 N /kg
EP = 8.9.8.10
EP = ?
EP = 1568
jul olur.
A.Ç
Örnek : Ağırlığı 80 N olan bir cismin
yerden 2 m yükseklikte sahip olduğu
potansiyel enerji,kaç jul’dür?
G = 80 N
h=2m
EP = G. h
EP = 80.2
EP = ?
EP = 160 jul
A.Ç
Soru :
m
m
m
3h
2h
h
1
2
3
Şekildeki kütleler özdeştir.Buna göre hangi
durumda potansiyel enerji en fazladır ?
A) 1
B) 2
C) 3
D ) Hepsi aynı
A.Ç
A.Ç
ENERJİ VE YAŞAM
İnsanoğlu günlük yaşantısının devamı için iş
yapmak ve enerji harcamak zorundadır.
İnsanın kendi kas gücüyle yaptığı işte hem
çabuk yorulur,hem de verimsiz olur.
Eski yıllarda köylüler işlerini ilkel tarım
aletleriyle yaparlardı.Bu yüzden kısa sürede
bitmesi gereken işler,çok uzun zamanda
yapılıyordu.
A.Ç
Çağımızda çok hızlı gelişen teknoloji
sayesinde,işlerimizi kolaylaştıran
aletler yapılmaktadır.Bugün bir çok
işimizi el değdirmeden
yapabiliyoruz.Örneğin bulaşık
makineleri, otomatik çamaşır
makineleri,robotlar bu işleri bizim
yerimize yapıyor.
A.Ç
Çağımız,hızlı makineleşme çağıdır.Enerji
olmadan bu makineler iş yapmaz.Enerji
yaşamımızın ayrılmaz bir parçası haline
gelmiştir.Enerji,gelişme sanayileşmenin
motor gücünü oluşturmaktadır.
Enerji kaynakları az olan ülkeler, geri
kalmış ülkelerdir.Günümüzde kişi başına
tüketilen enerji miktarı gelişmişliğin
ölçüsüdür.
A.Ç
Çağımızda çok yoğun bir enerjiye
gereksinim vardır. Enerji olmazsa yaşam
durur.Günümüz insanı enerjisiz yapamaz.
BU NEDENLE DOĞADAKİ ENERJİYİ
EKONOMİK KULLANMALIYIZ...
A.Ç
Hiçbir enerji kendi kendine var olmaz,kendi
kendine de yok olmaz.Fakat bir türden başka
bir tür enerjiye dönüşebilir.Bu dönüşüm
sırasında toplam enerji daima sabittir.Toplam
enerjinin sabit olması demek bir tür enerji
azalırken başka tür enerjinin aynı miktarda
artması demektir.Mesela belli bir yükseklikten
yere doğru hızlanarak düşen bir cismin kinetik
enerjisi artarken,aynı miktar potansiyel enerjisi
de azalmaktadır.
A.Ç
Barajda birikerek potansiyel enerji
kazanan su daha sonra yüksekten düşerek
kinetik,sonra elektrik ve oradan da ısı ve
ışık enerjisine dönüşmektedir.
Kısaca potansiyel enerji kinetik
enerjiye,kinetik enerji de potansiyel
enerjiye dönüşebilir. Bu değişmeler
sırasında toplam enerji değişmez.
İşte buna mekanik enerjinin korunumu
denir.
A.Ç
NOT: Sürtünme,önemsenmeyecek kadar az
olan sistemlerde kinetik ve potansiyel
enerjilerin toplamı sabittir. BUNA
MEKANİK ENERJİNİN KORUNUMU
DENİR.
EP + EK = SABİT
Örnek : Yüksekten akan suyun potansiyel
enerjisi,kinetik enerjiye dönüşür ve
türbini çalıştırır.Sıkıştırılmış yay serbest
bırakılırsa,ilk konumuna gelirken potansiyel
enerjisi kinetik enerjiye dönüşür...
A.Ç
A.Ç
A.Ç
GÜÇ NEDİR?
Birim zamanda üretilen veya tüketilen
enerjiye ( iş’e ) GÜÇ denir.
GÜÇ =
ENERJİ ( İŞ )
ZAMAN
Güç
W
P=
t
:P
Enerji : E
E
P=
t
Zaman : t
A.Ç
GÜÇ NEDİR?
jul
P = saniye = Watt
1000 watt = 1 kilowatt
1 kgm
= 9.8 watt
saniye
1 Buhar Beygiri ( BB ) = 736 wattt
1 B = 75 kgm / s
A.Ç
Örnek .Sürtünmesiz yatay bir düzlemde,durmakta olan bir cisme,hareketi
doğrultusunda 180 N ‘luk sabit bir kuvvet uygulanıyor. Cisim 1.5 dakikada 800 m
yer değiştiriyor. Kuvvetin yaptığı iş’ i ve gücü bulunuz?
Çözüm :
F = 180 N
A)
X = 800 m
W= F.X
W = 180 . 800
W=?
W = 144000 jul
B)
W = 144000 jul
P=
t = 1.5 dak = 90 saniye
P= ?
olur.
W
t
P=
14400 jul
90 saniye
P = 1600 watt = 1.6 k.w
A.Ç
Soru : Gücü 1200 watt olan bir
ütünün 30 saniyede harcadığı
elektrik enerjisini bulunuz ?
A.Ç
Soru : Gücü 2 kw olan bir araç,
80.000 jul’lük enerjiyi kaç saniyede
kullanır ?
A.Ç
Soru : 10 m derinliğindeki bir kuyudan
900 kg suyu 0.5 dakikada çekebilen
motorun gücü kaç BB dir ?
( 1 BB = 75 kgm / s )
A.Ç
Soru : Gücü 50 kgf / s olan motor,ağırlığı
150 kgf olan yükü 15 saniyede kaç metre
yukarı çıkarır?
A.Ç
A.Ç