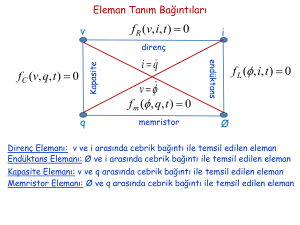
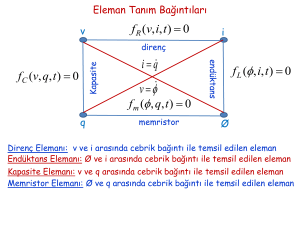
U.Arifoğlu
1
1.1. DÜŞÜRÜCÜ (BUCK) ÇEVİRİCİ DEVRE
Teorik bilgi:
Şekil 1.1'de verilen Buck (düşüren) çeviricide, yüke ilişkin ortalama gerilim değeri ( Vyük ), daima
devreyi besleyen doğru gerilim değerinden (E) küçüktür. Devrede yük olarak R direnci seçilmiştir. Bu
devrede yer alan anahtarlar iki adettir: Kontrollü anahtar (BJT), kontrolsüz anahtar (diyod). Devre iki
farklı modda çalışır. Şekil 1.2'de, her bir mod için elde edilen devre şemaları ve dalga şekilleri verilmiştir.
Mod 1, Q anahtarı t=0 anında iletime geçince başlar. Giriş akımı artarak, devrenin çıkış filtre elemanları
olan L ve C üzerinden yüke (R) ulaşır. Mod 2 ise, Q anahtarının t t1 anında kesime sokulması ile başlar.
Serbest geçiş diyodu olarak görev yapan D diyodu, mod 1'de L selfi üzerinden biriken enerji nedeni ile
iletime geçecektir. Q anahtarı tekrar iletime sokuluncaya kadar (L endüktansında enerji bitmediği
sürece), D diyodu akım akıtmaya devam edecektir. Endüktans akımı, L, C, R ve D üzerinden akım
akıtmaya bu modda devam eder. Q anahtarı tekrar tetikleninceye kadar endüktans akımı azalmaya
devam eder. Mod 2, Q anahtarının tekrar tetiklendiği T (periyod) anında sona erer. Aşağıda verilen
akım-gerilim değişimlerinde, akımın doğrusal olarak arttığı veya azaldığı kabul edilmiştir.
Uygulamalarda Q, D, L ve C elemanlarının küçük de olsa bir iç dirençleri vardır. Çoğu uygulamada bu
direnç etkileri ihmal edilir. Anahtarlama frekansına (f) bağlı olarak, L ve C içinden geçen akım kesintili
olabilir. Düşürücü çevirici, bir adet anahtar gerektirir, basit yapıdadır ve %90 üzerinde verime sahiptir.
Yük akımının değişimi L endüktansı tarafından sınırlandırılır. Ancak, giriş (kaynak) akımı, kesintilidir ve
normalde giriş akımını düzgünleştirecek endüktans (filtre) gerekir. Yük geriliminin polaritesi sabittir ve
çıkış akımı tek yöne akar. Diyodun kısa devre olmasına karşı koruma tedbiri alınmalıdır.
Şekil 1.1. Düşürücü (Buck) çevirici devre şeması
Düşürücü (Buck) çeviriciler iki farklı durumda çalışabilirler:
1) Sürekli akım durumu
2) Kesintili akım durumu
U.Arifoğlu
2
"Sürekli" ifadesi, L endüktansının üzerinden akan akımın bir periyod boyunca "devamlı" olması,
"süreksiz" ifadesi ise, L endüktansının üzerinden akan akımın bir periyod boyunca "kesintili" olması
anlamına gelmektedir. Endüktans akımının sürekli ya da süreksiz olması, devredeki D (duty cycle)
anahtarlama oranı (doluluk oranı), anahtarlama frekansı (f) ve yük değerine bağlıdır.
Şekil 1.2. Düşürücü devre çalışma mod eşdeğer devreleri ve dalga şekilleri
Devre, her iki çalışma durumu için ayrı ayrı incelenecektir.
1) Sürekli akım durumu
Şekil 1.2'de verilen akım ve gerilim değişimleri, sürekli çalışma durumuna ilişkindir. t=DT anına kadar
mod 1 çalışma durumu, t=DT anından t=T anına kadar ise, mod 2 çalışma durumu söz konusudur. Buna
göre D*T süresince mod 1, (1-D)*T süresince ise mod 2 durumu geçerli olacaktır. Şekil 1.2'den;
Vyük D * E
(1.1)
yazılabilir. Devredeki elemanların kayıpsız olduğu ve yük akımının düzgün olduğu kabul edilirse,
devredeki aktif güç eşitliğinden ( I giriş ; kaynak akımı ortalama değeri olmak üzere);
U.Arifoğlu
3
Pgiriş E * Igiriş Pyük Vyük * I yük D * E * I yük
(1.2)
Igiriş D * I yük
(1.3)
Şekil 1.3. Kaynak akımının değişimi
Şekil 1.4. Endüktans akımının kesintisiz olması durumu
yazılabilir. Şekil 1.3'de, kaynak akımının zaman bağlı değişimi verilmiştir. Şekil 1.4'de verilen,
endüktans akımının (maksimum ve minimum noktaları arasındaki fark) dalgalanma miktarı, t1 D * T;
Q anahtarının iletimde kaldığı süre, t 2 (1 D)T ; Q anahtarının kesimde kaldığı süre olarak kabul
edilirse, endüktans tanım bağıntıları kullanılarak;
T
I L * L I L * L
I L * L * E
1
t1 t 2
f
E Vyük
Vyük
Vyük (E Vyük )
(1.4)
elde edilir. (1.4) eşitliğinden, L endüktansındaki dalgalılık;
I L
Vyük (E Vyük )
f *L*E
(1.5)
veya;
I L
E * D(1 D)
f *L
(1.6)
olarak elde edilir.
Şekil 1.5'de, filtre kapasitesinin uçları arasındaki gerilimin değişimi, Şekil 1.6'da ise bu kapasite akımının
zamana bağlı değişimi görülmektedir. Filtre kapasitesinin (C) uçları arasındaki gerilimin dalgalanma
miktarı ise şöyle hesaplanır: Yükün bağlı olduğu düğüme kirchhoff akım yasası uygulanır ise;
i L (t ) i C (t ) i yük(t )
(1.7)
elde edilir. Yük akımının dalgalanma miktarının ( i yük ) ihmal edilecek kadar küçük olduğu kabulü ile,
(1.7) eşitliğinden;
U.Arifoğlu
4
i L ( t ) i C ( t )
(1.8)
yazılabilir. C kapasitesinden t1 / 2 t 2 / 2 T / 2 kadar süre boyunca artı yönde akan akımın ortalama
değeri;
IC
I L
;
4
Not: i L ( t ) eğrisinde:
T / 2 * I L / 2
I
IC * T / 2 IC L
2
4
(1.9)
olacaktır. C kondansatör gerilimi;
vC (t)
1
i C ( t )dt v C ( t 0)
C
(1.10)
olduğu düşünülürse, kondansatör geriliminin (maksimum ve minimum noktaları arasındaki fark)
dalgalanma miktarı;
Şekil 1.5. Filtre kapasitesi uçları arasındaki gerilimin değişimi
Şekil 1.6. Filtre kapasite akımının değişimi
VC v C ( t ) v C ( t 0)
I * T I L
1 T / 2 I L
dt L
C 0 4
8C
8fC
(1.11)
(1.5) veya (1.6) eşitliğindeki I L değeri, (1.11) eşitliğinde yerine yazılırsa;
VC
Vyük (E Vyük )
8LCf 2 E
(1.12)
veya
VC
E * D(1 D)
8LCf 2
(1.13)
elde edilir.
Şekil 1.4'de verilen dalga şekillerinden, bobin akımının minimum ve maksimum değeri, (1.5-6)
eşitlikleri kullanılarak;
I L _ min I yük
I L
E * D(1 D)
I yük
2
2f * L
(1.14)
U.Arifoğlu
5
I L _ min I yük
Vyük (E Vyük )
I L
I yük
2
2f * L * E
I L _ maks I yük
I L
E * D(1 D)
I yük
2
2f * L
I L _ maks I yük
Vyük (E Vyük )
I L
I yük
2
2f * L * E
(1.15)
(1.16)
(1.17)
elde edilir.
2) Süreksiz akım durumu
Şekil 1.7. Endüktans akımının kesintili akım durumu
Endüktans akımı ve kondansatör geriliminin sürekli olması için (Şekil 1.4'den), yük akımı ortalama
değerinin (veya endüktans akımı ortalama değerinin), endüktans akımı dalgalanma ( I L ) değeri ile yük
(ya da endüktans akımı ortalama değeri) arasında;
I L 2I L
(1.18)
ilişkisi vardır. I L 2I L "kritik koşulu" olması durumunda, kesinti-kesintisizlik sınırında çalışılıyor
demektir. Bu şartı sağlayan kritik endüktans değeri ( L krit ), (1.1) ve (1.6) eşitliklerini kullanarak;
Vyük (1 D)
f *L
2I L 2I yük
2DE
R
(1.19)
denkleminden kritik endüktans değeri;
L krit
(1 D)R
2f
(1.20)
Not: Devredeki L değeri, L krit değerinden küçük ise bobin akımında kesinti başlar.
Şekil 1.5'den, kapasite gerilimi ortalama değerinin (veya yük gerilimi ortalama değerinin), kapasite
gerilimi dalgalanma ( VC ) değeri ile yük (ya da yük gerilimi ortalama değeri) arasında;
U.Arifoğlu
6
VC 2Vyük
(1.21)
ilişkisi vardır. VC 2Vyük "kritik koşulu" olması durumunda, kesinti-kesintisizlik sınırında çalışılıyor
demektir. Bu şartı sağlayan kritik kapasite değeri ( C krit ), (1.1) ve (1.13) eşitliklerini kullanarak;
E(1 D)D
2Vyük 2DE
8LCf 2
(1.22)
denkleminden kritik kapasite değeri;
C krit
1 D
(1.23)
16 Lf 2
olarak bulunur.
Not: Devredeki C değeri, Ckrit değerinden küçük ise kapasite geriliminde kesinti başlar.
Önemli not: Ckrit değeri, yük akımı dalgalılığının ( i yük ) ihmal edilecek kadar küçük değerler aldığı
durumlarda geçerlidir. Bu durum ise ancak, f anahtarlama frekansının yüksek değerler alması
durumunda mümkün olabilir. Eğer, anahtar (f) tetikleme frekansı (deneyde kullandığınız; 1000, 500 Hz
gibi) çok küçük değerler alırsa, çıkış geriliminin minimum değerinin, (1.23) eşitliği ile hesaplanan Ckrit
değeri için, sıfır volt'a inmesini beklemek, doğru bir yaklaşım olmaz.
Şekil 1.1'de verilen devrede, L endüktansı uçları arasındaki gerilimin ortalama değeri sıfır olduğundan
(Şekil 1.7'den);
(E Vyük)DT Vyük * 1 * T 0
Vyük
E
D
D 1
(1.24)
(1.25)
elde edilir. L endüktans tanım bağıntısından, endüktans akımı tepe değeri;
v L (t ) L
I L _ maks
di L ( t )
E Vyük L
dt
DT
I L _ max
(E Vyük )DT
(1.26)
(1.27)
L
veya
v L (t ) L
0 I L _ maks
di L (t )
Vyük L
dt
1T
I L _ maks
Vyük1T
(1.28)
(1.29)
L
elde edilir. Endüktans akımı ortalama değeri, yük akımı ortalama değerine eşit olduğundan, endüktans
akımının ortalaması;
I yükT I LT (D 1)T
I L _ maks
2
(1.30)
U.Arifoğlu
7
yazılabilir. (1.30) eşitliğinde, (1.29) eşitliği kullanılırsa;
I yük
(D 1)Vyük1T
(1.31)
2L
elde edilir. (1.31) eşitliğinde, (1.25) eşitliği kullanılırsa;
I yük
ED 1T
2L
(1.32)
elde edilir.
Şekil 1.8. Endüktans akımının kesintili-kesintisiz akım sınırında olması
Şekil 1.8'den, endüktans akımının kesintili-kesintisiz akım sınırındaki ortalama akım değeri; I L _ sınır
ve bu durumdaki endüktans akımı tepe değeri; I L _ sınır _ tepe olmak üzere, endüktans tanım
bağıntısından;
v L (t) L
I L _ sınır _ tepe 0
di L ( t )
E Vyük L
dt
DT
(1.33)
ve bobin akımı ortalama (dolayısı ile yük akımı değerinden) yola çıkarak;
T * I L _ sınır
I L _ sınır _ tepe * DT
2
I L _ sınır
D * I L _ sınır _ tepe
2
(1.34)
yazılabilir. Kesintili-kesintisiz akım sınırındaki endüktans tanım bağıntısından;
v L (t ) L
I L _ tepe_ sınır
di L ( t )
E Vyük L
dt
DT
I L _ sınır _ tepe
I L _ sınır
(E Vyük )DT
L
(E Vyük )D 2T
2L
(1.35)
(1.36)
(1.37)
veya
v L (t) L
Vyük L
0 I L _ sınır _ tepe
di L (t )
Vyük L
dt
(1 D)T
I L _ sınır _ tepe
(1 D)T
(1.38)
(1.39)
U.Arifoğlu
I L _ sınır
8
D(1 D)TVyük
(1.40)
2L
olacaktır.
Örnek Problem
Sürekli akım modunda, alçaltıcı bir çeviricide; Vgiriş 12 V, R=500 ohm, Vyük 5 V, VC 20 mV ,
IL 0.8 A, f=25 kHz olduğuna göre;
a) D=?
b)L=?
d) L krit ?
c)C=?
e) Ckrit ? değerlerini hesaplayınız.
Çözüm
a) Vyük D * E D
b) I L
5
%41 .67
12
Vyük(E Vyük)
f *L*E
I
L
5(12 5)
145 .83H
0.8 * 25000 *12
0.8
c) VC L C
200 F
8fC
8 * 20 *10 3 * 25000
d) L krit
e) Ckrit
(1 D)R (1 0.4167 ) * 500
5.83mH
2f
2 * 25 *10 3
1 D
16 Lf 2
1 0.4167
16 *145 .83 *10 6 * (25 *10 3 ) 2
0.4F
U.Arifoğlu
9
1.2. YÜKSELTİCİ (BOOST) ÇEVİRİCİ DEVRE
Teorik bilgi:
Şekil 1.9(a)'da verilen BOOST (yükselten) çeviricide, yüke ilişkin ortalama gerilim değeri ( Vyük ), daima
devreyi besleyen doğru gerilim değerinden (E) yüksektir. Devrede yük olarak R direnci seçilmiştir. Bu
devrede yer alan anahtarlar iki adettir: Kontrollü anahtar (MOSFET), kontrolsüz anahtar (diyod). Devre
iki farklı modda çalışır. Şekil 1.9(c)'de, her bir mod için elde edilen devre şemaları ve dalga şekilleri
verilmiştir. Mod 1, Q anahtarı t=0 anında iletime geçince başlar. Giriş akımı artarak, devrenin çıkış filtre
elemanı olan L endüktansı ve Q anahtarı üzerinden geçer. Mod 2 ise, Q anahtarının t t1 anında kesime
sokulması ile başlar. Daha önce L endüktansı üzerinden geçen akım, bu modda, D diyodu, L endüktansı
ve C kapasitesi üzerinden yüke ulaşır. Q anahtarı tekrar iletime sokuluncaya kadar L endüktans akımı
azalmaya devam edecektir. L endüktansı üzerinde mod 1'de depolanan enerji bu modda yük üzerine
aktarılır. Q anahtarı tekrar tetikleninceye kadar endüktans akımı azalmaya devam eder. Mod 2, Q
anahtarının tekrar tetiklendiği T (periyod) anında sona erer. Şekil 1.9(d)'de verilen akım-gerilim
değişimlerinde, akımın doğrusal olarak arttığı veya azaldığı kabul edilmiştir. Uygulamalarda Q, D, L ve
C elemanlarının küçük de olsa bir iç dirençleri vardır. Çoğu uygulamada bu direnç etkileri ihmal edilir.
Anahtarlama frekansına (f) bağlı olarak, L ve C içinden geçen akım kesintili olabilir.
Şekil 1.9
U.Arifoğlu
10
Yükselten çevirici, transformatör olmaksızın gerilim yükseltebilmektedir. Devrede bir adet anahtar
olduğu için yüksek bir verime sahiptir. Giriş akımı süreklidir, ancak, yüksek değerli bir akım anahtar
üzerinden akmaktadır. Çıkış (yük) gerilimi D doluluk oranına çok hassastır. Bu nedenle çeviricinin kararlı
çalışmasını temin etmek zor olabilir. Ortalama çıkış akımı (yük akımı), ortalama endüktans akımından
(1-D) oranında küçük değerdedir. Bu nedenle çıkış (filtre) kondansatöründen akan akımın etkin değeri
çok daha yüksek olur. Bundan dolayı, BUCK çeviriciye oranla, BOOST çeviricide kullanılan L ve C
değerinden daha yüksek değerde L ve C kullanılması gerekir.
Yükseltici (Boost) çeviriciler iki farklı durumda çalışabilirler:
1) Sürekli akım durumu
2) Kesintili akım durumu
"Sürekli" ifadesi, L endüktansının üzerinden akan akımın bir periyod boyunca "devamlı" olması,
"süreksiz" ifadesi ise, L endüktansının üzerinden akan akımın bir periyod boyunca "kesintili" olması
anlamına gelmektedir. Endüktans akımının sürekli ya da süreksiz olması, devredeki D (duty cycle)
anahtarlama oranı (doluluk oranı), anahtarlama frekansı (f) ve yük değerine bağlıdır.
Devre, her iki çalışma durumu için ayrı ayrı incelenecektir.
1) Sürekli akım durumu
Şekil 1.10. Endüktans akımının kesintisiz akım durumu
Şekil 1.9(d)'de verilen akım ve gerilim değişimleri, sürekli çalışma durumuna ilişkindir. t=DT anına kadar
mod 1 çalışma durumu, t=DT anından t=T anına kadar ise, mod 2 çalışma durumu söz konusudur. Buna
göre D*T süresince mod 1, (1-D)*T süresince ise mod 2 durumu geçerli olacaktır. Şekil 1.10'da
endüktans geriliminin ortalama değerinin sıfır olması gerektiği prensibinden;
E * DT (E Vyük)(1 D)T 0 Vyük
E
1 D
(1.41)
yazılabilir. Devredeki elemanların kayıpsız olduğu ve yük akımının düzgün olduğu kabul edilirse,
devredeki aktif güç eşitliğinden ( I giriş ; kaynak akımı ortalama değeri olmak üzere);
Pgiriş E * Igiriş Pyük Vyük * I yük
Igiriş
E
* I yük
1 D
1
* I yük
1 D
Yükseltici çeviricide, endüktans akımı, kaynak akımına eşittir.
(1.42)
(1.43)
U.Arifoğlu
11
Şekil 1.4'de verilen, endüktans akımının (maksimum ve minimum noktaları arasındaki fark)
dalgalanma miktarı, t1 D * T; Q anahtarının iletimde kaldığı süre, t 2 (1 D)T ; Q anahtarının kesimde
kaldığı süre olarak kabul edilirse, endüktans tanım bağıntıları kullanılarak;
T
I L * L * Vyük
1
I * L I L * L
t1 t 2 L
f
E
Vyük E
E(Vyük E)
(1.44)
elde edilir. (1.4) eşitliğinden, L endüktansındaki dalgalılık;
I L
E(Vyük E)
(1.45)
f * L * Vyük
veya;
I L
E*D
f *L
(1.46)
olarak elde edilir.
0 t t1 aralığında, mosfet ilerimdeyken, yük akımını C kondansatörü temin eder. Bu süre boyunca
ortalama kondansatör akımı, yük akımı ortalama değerine eşit olur ( IC I yük ). Kondansatörde
tepeden tepeye dalgalanma gerilimi ise;
0
0
1
t1I yük
1
t1
VC v C ( t t1 ) v C ( t 0) 0 i C ( t )dt 0t1 i yük ( t )dt
C
C
C
(1.47)
olacaktır. (1.44) eşitliğinden t1 'in karşılığı çekilir, (1.45) eşitliğinde karşılığı yazılırsa;
VC
t1I yük
C
I L * L * I yük
CE
(Vyük E)I yük
CfV yük
(1.48)
veya (1.41) eşitliğinden;
VC
t1I yük
C
I L * L * I yük
CE
DI yük
Cf
(1.49)
elde edilir. Şekil 1.10'da verilen dalga şekillerinden, bobin akımının minimum ve maksimum değeri,
(1.45-46) eşitlikleri kullanılarak;
I L _ min I yük
E(Vyük E)
I L
I yük
2
2f * L * Vyük
I L _ min I yük
I L
E*D
I yük
2
2f * L
(1.50)
(1.51)
I L _ maks I yük
E(Vyük E)
I L
I yük
2
2f * L * Vyük
(1.52)
I L _ maks I yük
I L
E*D
I yük
2
2f * L
(1.53)
U.Arifoğlu
12
elde edilir.
Endüktans akımı ve kondansatör geriliminin sürekli olması için (Şekil 1.11'den), endüktans akımı
dalgalanma ( I L ) değeri ile endüktans akımı ortalama değeri arasında;
I L 2I L
(1.54)
ilişkisi vardır. I L 2I L "kritik koşulu" olması durumunda, kesinti-kesintisizlik sınırında çalışılıyor
demektir. Bu şartı sağlayan kritik endüktans değeri ( L krit ), (1.41) ve (1.46) eşitliklerini kullanarak;
Şekil 1.11. Endüktans akımının kesintili-kesintisiz akım sınırında olması
ED
2E
2I L 2I giriş
f *L
(1 D) 2
(1.55)
denkleminde, E= (1 D)Vyük ve (1.43) eşitliğini kullanarak, kritik endüktans değeri;
L krit
D(1 D) 2 R
2f
(1.56)
olarak bulunur.
Şekil 1.5'den, kapasite gerilimi ortalama değerinin (veya yük gerilimi ortalama değerinin), kapasite
gerilimi dalgalanma ( VC ) değeri ile yük (ya da yük gerilimi ortalama değeri) arasında;
VC 2Vyük
(1.57)
ilişkisi vardır. VC 2Vyük "kritik koşulu" olması durumunda, kesinti-kesintisizlik sınırında çalışılıyor
demektir. Bu şartı sağlayan kritik kapasite değeri ( C krit ), (1.49) eşitliğini kullanarak;
I yükD
Cf
2Vyük 2I yükR
(1.58)
denkleminden, kritik kapasite değeri;
C krit
D
2Rf
(1.59)
olarak bulunur. Şekil 1.1'de verilen devrede, L endüktansı uçları arasındaki gerilimin ortalama değeri
Not: Devredeki C değeri, Ckrit değerinden küçük ise kapasite geriliminde kesinti başlar.
U.Arifoğlu
13
Önemli not: Ckrit değeri, yük akımı dalgalılığının ( i yük ) ihmal edilecek kadar küçük değerler aldığı
durumlarda geçerlidir. Bu durum ise ancak, f anahtarlama frekansının yüksek değerler alması
durumunda mümkün olabilir. Eğer, anahtar (f) tetikleme frekansı (deneyde kullandığınız; 1000, 500 Hz
gibi) çok küçük değerler alırsa, çıkış geriliminin minimum değerinin, (1.23) eşitliği ile hesaplanan Ckrit
değeri için, sıfır volt'a inmesini beklemek, doğru bir yaklaşım olmaz.
2) Kesintili akım durumu
Şekil 1.12. Endüktans akımının kesintili akım durumu
Şekil 1.12'de verilen devrede, L endüktansı uçları arasındaki gerilimin ortalama değeri sıfır olduğundan
(Şekil 1.7'den);
EDT (E Vyük) * 1 * T 0
Vyük
E
(1.60)
D 1
1
(1.61)
elde edilir.
Devrede aktif güç kaybı olmadığı kabulü ile;
Pgiriş E * Igiriş Pyük Vyük * I yük
(D 1)E
* I yük
1
(1.62)
devrenin giriş ve çıkış akımları arasında;
Igiriş
(D 1)
* I yük
1
(1.63)
eşitliği elde edilir.
L endüktans tanım bağıntısından, endüktans akımı tepe değeri;
vL (t ) L
I L _ maks
diL ( t )
EL
dt
DT
(1.64)
U.Arifoğlu
14
EDT
L
(1.65)
0 I L _ maks
di L ( t )
E Vyük L
dt
1T
(1.66)
I L _ max
veya
v L (t) L
(Vyük E )1T
I L _ maks
(1.67)
L
elde edilir. Endüktans akımı ortalama değeri, giriş akımı ortalama değerine eşit olduğundan, endüktans
akımının ortalaması;
I giriş T I L T (D 1 )T
I L _ maks
(1.68)
2
yazılabilir. (1.68) eşitliğinde, (1.61) ve (1.67) eşitliği kullanılırsa;
Igiriş (D 1)
EDT
2L
(1.69)
elde edilir. (1.69) eşitliği, (1.63) eşitliğinde kullanılırsa;
I yük
EDT1
2L
(1.70)
elde edilir. (1.70) eşitliği, 1 değerini bulmak için de kullanılabilir.
Örnek Problem
Sürekli akım modunda, yükseltici bir çeviricide; Vgiriş E 5 V, Vyük 15 V, I yük 0.5A , f=25 kHz ,
L= 150 μH, C=220 μF olduğuna göre;
b) IL =?
a) D=?
c) I L _ maks =?
d) VC =?
e) L krit ve C krit değerlerini hesaplayınız.
Çözüm
a) Vyük
E (Vyük E )
5(15 5)
E
5
0.89 A
15 D %66 .67 ; b) I L
f * L * Vyük 25000 *150 *10 6 *15
1 D 1 D
c) I L _ maks I yük
DI yük
d) VC
Cf
e) R
Vyük
I yük
L krit
I L
0.89
0.5
1.945 A
2
2
0.6667 * 0.5
220 *10 6 * 25 *10 3
60 .61mV
15
30 ohm
0.5
D(1 D) 2 R 0.6667 (1 0.6667 ) 2 30
133 H ;
2f
2 * 25 *10 3 * 30
Ckrit
D
0.6667
0.44F
2fR 2 * 25 *10 3 * 30