deney

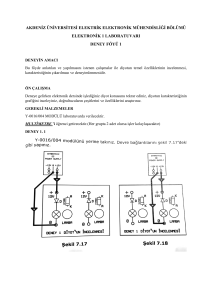
BÖLÜM 2
YARI İLETKEN DİYOT
Amaç: p-n eklem diyot ile zener diyotun özelliklerinin incelenmesi ve davranışlarının
belirlenmesi.
BİLGİ
2.1 Yarı İletken: Yarı iletken devre elemanlarının yapımında saflaştırılmış ve gerektiği
şekilde kristalleştirilmiş silisyum (Si) veya Germanyum (Ge) kullanılır. Düzgün kristal
yapıdaki böyle bir yarı iletken malzemeye yabancı atomlar (örneğin P,As,...v.s) katılırsa,
“serbest elektronlar” çoğaltılabilir. Bunlarla birlikte, ısıl uyarma sonucu yarı iletken malzeme
atomlarından kopan elektronlar da vardır. Bu kopmalarla oluşan elektron noksanlığı çok
zaman o yerlerde pozitif yüklerin kaldığı şekilde yorumlanır. Bu sözde pozitif yüke delik
(deşik) denir. Delikler de, komşu atomlardan çalınan elektronlarla doldurmaları sonucu
rasgele hareket ederler. Bir elektrik alan uygulandığında delikler de elektronlar gibi alanın
belirlediği yönde sürüklenerek bir akıma neden olurlar. Deliklerle elektronların alanın etkisi
ile hareket yönleri zıt olduğu halde taşıdıkları yükler de zıt işaretli olduğundan oluşturdukları
akımlar aynı yönde, pozitiften negatife doğrudur.
Sonuç olarak yabancı atomlarla katkılanmış bir yarı iletkenin cinsine göre, ya çok sayıda
elektron ve az sayıda delik ya da çokça delik ve az elektron bulunduğu söylenebilir. Fazla
sayıdaki taşıyıcılar çok zaman çoğunluk taşıyıcıları, diğerleri ise azınlık taşıyıcıları olarak
anılırlar. Çoğunluk taşıyıcıları negatif yükler, yani elektronlar olan bir yarı iletken n-tipi
olarak isimlendirilir. Diğer türe ise p-tipi denir.
Katkı atomları katılmış bir yarı iletkende belirli bir sıcaklıkta, bu taşıyıcı yoğunlukları
çarpımının sabit olduğu gösterilebilir. Ancak bunların taşıyıcı yoğunluğu, saf yarı iletkenlere
göre daha büyüktür. Dolayısıyla katkılanmış yarı iletkenlerin iletkenlikleri daha
mükemmeldir.
2.2 p-n Eklemi: Bir yarı iletkenin bir
kısmı p-tipi, diğeri n-tipi olacak şekilde
katkılanırsa, birbirlerine komşu iki farklı
bölge ile bunların sınır bölgesi, yani p-n
eklemi (p-n jonksiyonu) gerçekleşir. Yarı
iletkenin elektron verici (donör) atomlarla
katkılanması n-tipi yarı iletkeni, elektron
alıcı (akseptör) atomlarla katkılanması ise
p-tipi yarı iletkeni oluşturur (Şekil 2.1). Bu
şekilde oluşturulan p-n ekleminde, örneğin
p-tipi bölgedeki büyük yoğunluktaki
delikler n-tipine doğru, n-tipi bölgedeki
çoğunluktaki elektronlar p-tipine doğru yayılırlar. Bu olaya “difüzyon” denir. Ancak bu olay
sürüp gidemez. Belirli bir süre sonra yüklerin hareketleri durur.
Bir p-n ekleminde p-tipi bölgeye negatif, n-tipi bölgeye ise pozitif gerilim uygulanırsa; oluşan
elektrik alan, yüklerin hareketini önemli ölçüde engeller. Dolayısıyla eklemden hemen hemen
hiç akım akmaz. Böyle bir gerilim uygulanması “tıkama yönünde kutuplama” olarak anılır.
Bunu tersi halinde, yani p-tipi bölgeye pozitif gerilim uygulanması durumunda ise eklemden
büyük akım akar. Bu durum “geçirme yönünde kutuplama” olarak adlandırılır.
Sonuç olarak geçirme yönünde kutuplanan bir p-n ekleminin büyük miktarda akım
akıtabilmesine karşılık; tıkama yönünde kutuplanmasında ise çok çok küçük bir akım akıttığı
söylenebilir.
2.3 Yari İletken Diyot: Bir p-n eklemi, p-tipi bölgesi n-tipi bölgesine göre negatif olduğunda
çok çok küçük akım; ancak tersi durumda büyük bir akım akıtabildiğine göre; bir yönde akım
geçiren bir devre elemanı, yani diyot olarak kullanılabilir. Bu nedenle bir p-n eklemi yarı
iletken diyot işlevini görür.
Böyle bir diyot şematik olarak Şekil
2.2’deki gibi gösterilir. Bu şekildeki gibi
geçirme yönünde kutuplanmış bir diyotta
p-n ekleminden geçen net akım, n-tipinden
p-tipine geçen elektronların oluşturduğu
akımla p-tipinden n-tipine geçen deliklerin
oluşturduğu akımın toplamıdır.
Yarı iletken bir diyotun ideal akım-gerilim
eğrisi Şekil 2.3’deki gibidir. Bu şekilde,
tıkama yönünde kutuplanmış diyottan
geçen ve tıkama yönü doyma akımı olarak
adlandırılan I 0 akımının gösterilebilmesi
için ölçeğin bu kısmının genişletilmiş
olduğuna dikkat edilmelidir; zira bu akımın
değeri A mertebesindedir.
Gerçekte bir diyotun elektriksel davranışı,
diyotun öz eğrisi olarak adlandırılan bu
değişime pek uymaz. Şekil 2.4’de verilen
gerçek akım-gerilim öz eğrilerinden
anlaşılabileceği üzere, V D gibi bir “eşik
gerilimi” olarak isimlendirilen bir gerilim
değerinin altında diyotun akıttığı akım çok
küçüktür. Bu değer Si diyotlarda 0,7V, Ge
diyotlar ise 0,3V civarındadır.
Diyot karakteristiklerinden biri de R f ,
“diyot direnci” olarak anılan diyotun
çalışma durumunda uçları arasındaki V
geriliminin diyottan geçen akıma oranı
olarak tanımlanan V/I büyüklüğüdür.
Ancak bu R f büyüklüğü V ve I’ye bağımlı olarak çok fazla değişir. Bu nedenle de I akım
aralığındaki V değişimine bağlı olarak,
Rf 
V V2  V1

I
I 2  I1
(2.1)
şeklinde tanımlanması daha uygundur.
2.4 Zener Diyot: Şekil 2.3’den de anlaşılacağı gibi, tıkama akımı belirli bir tıkama gerilimine
kadar sabit kalmakta; ancak bir V z tıkama geriliminde birden bire artmaktadır: Bu gerilim,
zener gerilimi olarak adlandırılır. Böyle bir çalışmaya olanak sağlayacak şekilde
gerçekleştirilen diyotlar sabit (referans) gerilim düzeni olarak kullanılabilirler.
Böyle bir diyot zener diyot olarak anılır ve
Şekil 2.5’deki
sembolle gösterilir.
Genellikle bu şekilde gösterildikleri gibi
kullanılan zener diyotlar, V besleme
gerilimi veya I L yük akımı değişimlerine
karşı
yük direnci uçları arasındaki
gerilimin sabit kalmasını sağlarlar. Zira,
Şekil 2.3’den de anlaşılacağı üzere I z
diyot akımındaki büyük değişmeler bile V z
diyot geriliminde gayet küçük değişime neden olurlar.
DENEY
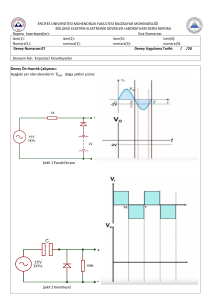
A)p-n Eklem Diyotun Özellikleri:
1)Şekil 2.6’daki devre Digiac 3000-2.1
Semiconductors-1 modülünün 1 nolu
düzeninden yararlanarak gerçekleştirilir.
Diyotun uçları arasındaki V gerilimi 0-2V
DC gerilim kaynağı ile değiştirilir.
Osiloskopta ölçülen V gerilimleri Tablo
2.1’de verilen değerlere ayarlanarak,
diyottan geçen akım
ampermetre olarak
kullanılan DM ile ölçülür, sonuçlar Tablo
2.1’e geçirilir.
2)Tablo 2.1’deki sonuçlardan yararlanılarak yarı iletken diyotun öz eğrisi (Şekil 2.4) çizilir.
Tablo 2.1
V mV 
850
I
800
750
700
650
600
550
500
400
300
200
100
3)Şekil 2.7’deki devre gerçekleştirilir. 0-12V DC gerilim kaynağı ile uygulanan gerilim
değiştirilerek devreden geçen akım DM ile izlenir. Sonuçlar yorumlanır.
4)Şekil 2.7’deki devreden ampermetre olarak kullanılan DM çıkarılır. DC voltmetre olarak
kullanılan DM ile diyot uçları arasındaki gerilim 0-12V DC gerilim kaynağı ile –1V’a
ayarlanır. DM yardımıyla R 2 direnci üzerindeki gerilim düşmesi ölçülür ve Tablo 2.2’ye
işlenir. Bu değerlerden, Ohm kanunu yardımıyla diyotun tıkama yönü doyma akımı (sızma
akımı) hesaplanır.
5)Bu
işlem
Tablo
2.2’deki
değerler
için
tekrarlanır,
sonuçlar
tabloya
geçirilir.
Tablo 2.2
Anot gerilimi V 
VR 2  mV 
Sızma akımı nA
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
6)Diyotun ileri ve ters yöndeki dirençlerini ölçmek için diyot devreden ayrılır (Devreye hiçbir
gerilim uygulanmaz). Ohmmetre olarak kullanılan DM ile diyotun geçirme (ileri) ve tıkama
(geri) yönlerdeki dirençleri ölçülür, sonuçlar Tablo 2.3’e işlenir. (İleri yöndeki ölçümlerde
Ohmmetre ile elemana uygulanan DC gerilimin (+) ucunun bağlanmasının gerektiği
unutulmamalıdır.)
Tablo 2.3
Diyot
Direnç
İleri yön
Geri yön
B) Zener Diyotun Karakteristikleri:
1)Şekil 2.8’deki devre Digiac 3000-2.1
Semiconductors-1
modülünün 6 nolu
düzeniyle gerçekleştirilir. Zener diyotun
uçları arasındaki gerilim 0-2V DC gerilim
kaynağı ile Tablo 2.4’deki değerlere
ayarlanır.
Devreden
geçen
akım
osiloskopla 22 ’luk R8 direnci uçları
arasındaki gerilim düşmesi ölçülerek
hesaplanır, sonuçlar Tablo 2.4’e işlenir.
Tablo 2.4
Vz V 
0,60
0,65
0,70
0,75
0,80
2)Bu devrede bazı değişiklikler yapılarak;
Şekil 2.9’daki devre gerçekleştirilir.
Osiloskop yardımıyla ölçülen zener diyot
uçları arasındaki gerilim 0-12V
DC
gerilim kaynağı ile 1V’a ayarlanır (bu
gerilimi zener diyota göre negatif bir
gerilimdir; zira pozitif gerilim zener
diyotun katoduna uygulanmıştır). DM ile
devreden geçen akım ölçülür ve sonuç
Tablo 2.5’e işlenir.
VR8  mV 
I (mA)
Tablo 2.5
I   A
Vz (V )
1
2
3
4
4,2
4,4
4,6
3)Bu işlem Tablo 2.5’deki değerler için tekrarlanır ve sonuçlar tabloya geçirilir.
4)Tablo 2.4 ve Tablo 2.5’deki verilerden faydalanılarak zener diyotun öz eğrisi çizilir.
5)Şekil 2.9’daki devreden faydalanılarak Tablo 2.6’daki akım değerlerine karşılık gelen ve
osiloskop yardımıyla ölçülen zener diyotun uçları arasındaki gerilim değerleri tabloya
geçirilir.
Tablo 2.6
I mA
I1
I2
I3
I4
2
4
6
8
Vz V 
V1
V2
V3
V4
6)Tablo 2.6’dan elde edilen sonuçlardan faydalanılarak, (2.1) bağıntısının da yardımı ile zener
diyotun, geçen akıma bağlı Rz direnci hesaplanır, sonuç Tablo 2.7’ye işlenir.
Tablo 2.7
Rz
2-4mA
4-6mA
6-8mA
7)Şekil 2.10’daki devrede R9 yük direnci
üzerinden geçen I L
yük akımı ve
devreden geçen toplam
I
akımı
hesaplanır. Burada I akımı I L ’den %20
daha fazla olması uygundur. Böylece
devreye
uygulanması
gereken
Vin
potansiyel farkı hesaplanır. Bu değerlerden
I z zener akımı da hesaplanarak Tablo
2.8’e yazılır.
8)Bu devreye hesaplanan Vin potansiyel değeri uygulanır ve Tablo 2.8’deki akım değerleri
DM ile ölçülür.
Tablo 2.8
I
Iz
IL
I L I z
I hesap
I ölçüm
9)Bu değerlerden I akımı ile hesaplanan I L  I z akımı kıyaslanır.
10)Şekil 2.11’deki devre gerçekleştirilerek
0-12V DC gerilim kaynağı maksimuma
getirilir. Devredeki DM’nin bir ucu
sökülerek I L yük akımı sıfırlanır, bu
durumda osiloskopla V z zener gerilimi
ölçülür. Sonuçlar Tablo 2.9’a işlenir.
11)Bu işlem, Ryük direnci değiştirilerek
Tablo 2.9’daki I L akımı değerleri için
tekrarlanır, sonuçlar Tabloya geçirilir.
Tablo 2.9
I L mA
Vz
0
1
2
4
6
8
10
12
14
16
18
20
22
24
27
12)Bu değerlerden V z çıkış geriliminin, I L yük akımına bağlı Vz  f I L  değişimi çizilir.
13)Zener diyotta harcanan gücün belirlenebilmesi için bu devrede bazı değişiklikler yapılarak
Şekil 2.12’deki devre gerçekleştirilir.
14) Bu durumda zener diyottan geçen
I z ,max , maksimum akımı ile uçları
arasındaki V z gerilimi ölçülür, sonuçlar
Tablo 2.10’a işlenir.
15)Bu değerlerden, bilinen güç bağıntısı ile
zener diyotta harcanan P gücü hesaplanır,
sonuç Tablo 2.10’a geçirilir.
Tablo 2.10
I z ,max
Vz
P
SORULAR
1)Geçirme yönünde kutuplanmış bir Si diyotun akım akıtabilmesi için uçları arasındaki
gerilim farkı en az ne kadar olmalıdır?
2)Bir diyotun sızma akımı neden standart bir ölçü aleti ile ölçülemez?
3)Tıkama yönünde kutuplanmış bir zener diyotun direnci yaklaşık ne kadardır?
4)Bir zener diyotla paralel bağlı bir yük direncinin uçları arasındaki gerilim nasıl değişebilir?