Teorik Dağılımlar

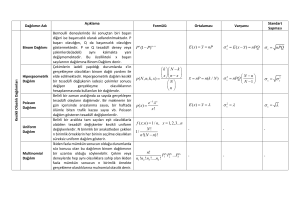
TEORİK DAĞILIMLAR
İlgilenilen bir olayın gerçekleşme durumu, teorik bir
dağılıma uyuyor ise olayın gerçekleşme olasılığı
hesaplanarak olası sonuçlar tahmin edilebilir. Çok
sayıda teorik dağılım mevcuttur. Veteriner Hekimlik
alanında sıkça kullanılan dağılımlar;
1- Binomiyal Dağılım
2- Poisson Dağılım
3- Normal Dağılım
Binomiyal Dağılım
Sayımla belirtilen kesikli değişkenlerin dağılımıdır.
Bir olayın (p) oluş olasılığının büyük, n denek sayısının küçük
olduğu durumlarda olasılık hesaplanmasında kullanılır.
Binomiyal dağılımda incelenen olayın birbirinden bağımsız iki
olası sonucu vardır.
Binom dağılımında denemeler birbirinden bağımsızdır. Bir
sonucun ortaya çıkması diğer olayın ortaya çıkmasını etkilemez.
n
P(r )   
r 
r
pq
nr
r
nr
n!

r  0,1,2,..., n
p
q
(n  r )! r!
n: Toplam olay sayısı r: İstenen olayın oluş sayısı
p: İstenen olayın gerçekleşme olasılığı q: İstenen olayın gerçekleşmeme olasılığı
Binomiyal Dağılım
Doğum esnasında bir domuz yavrusunun dişi olma olasılığı
%50’dir. Ultrason sonucu 4 yavru doğurması beklenen bir dişi
domuzun 1,2 ve 3 yavrusunun dişi olma olasılığı hesaplansın

4
p(1)   0,51x (10,5)41 4! 0,51x (10,5)41 0,25
(4 1)!1!
1 






4
p(2)   0,52 x (10,5)42  4! 0,52 x (10,5)42  0,375
(4  2)!2!
2






4
p(3)   0,53 x (10,5)43  4! 0,53 x (10,5)43  0,25
(4 3)!3!
3 





Poisson Dağılımı
Sayımla belirtilen değişkenlerin dağılımıdır. İncelenen olayın görülme
olasılığı (p) küçük, n büyük olduğunda olasılık hesaplamak için
kullanılır.
r

x
X
P(r ) 
r! e
r: İstenen olayın oluş sayısı
Bir bölgedeki veteriner kliniğine gece muayene için gelen hasta
sayısının Poisson dağılım gösterdiği bilinsin, Kliniğe gece ortalama 4
hasta geldiğine göre; Herhangi bir gece kliniğe 2 hasta gelme olasılığı
2
P(2)  4 e
2!
4
16
 0,018  0,144
2
Normal Dağılım
Ölçümle belirtilen (sürekli) değişkenlerin
dağılımıdır. Birden fazla dağılım vardır.
- Normal dağılım ortalamaya göre simetriktir.
- Eğri ile x ekseni arasındaki toplam alan 1
birim karedir.
- Aritmetik ortalama, ortanca ve tepe değeri
birbirine eşittir.
Standart Normal Dağılım
Her farklı ortalama ve standart sapma farklı dağılımlar ürettiğinden, her dağılım
için ayrı eğri altında alan hesaplamasının getireceği hesaplama zorluklarından
kurtulmak için dağılımın standart tek bir dağılıma dönüştürülmesi yoluna
gidilmiştir. Standartlaştırma için uygulanılan formül;
z  x s x
z1 
Örnek: Bir toplumda kan basıncı değerlerinin ortalamasının 130
mmHg, standart sapmasının 25 mmHg ile normal dağılım
gösterdiği bilinmektedir.
x  xarasında bulunan kişi yüzdesi nedir?
z mmHg
-Kan basıncı 110-140
s
110  130
 0,8
25
z2 
140  130
 0,4
25
Z1=0,2881
Z2=0,1554
+
0,4435