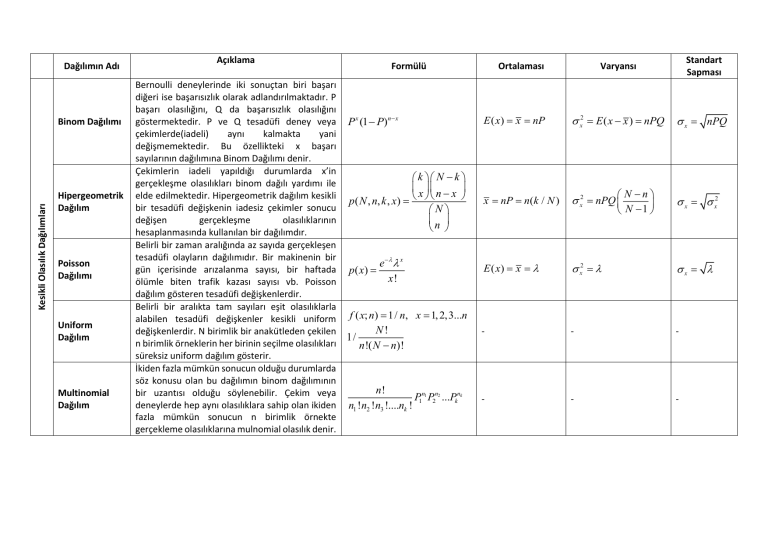
Dağılımın Adı
Kesikli Olasılık Dağılımları
Binom Dağılımı
Hipergeometrik
Dağılım
Poisson
Dağılımı
Uniform
Dağılım
Multinomial
Dağılım
Açıklama
Bernoulli deneylerinde iki sonuçtan biri başarı
diğeri ise başarısızlık olarak adlandırılmaktadır. P
başarı olasılığını, Q da başarısızlık olasılığını
göstermektedir. P ve Q tesadüfi deney veya
çekimlerde(iadeli)
aynı
kalmakta
yani
değişmemektedir. Bu özellikteki x başarı
sayılarının dağılımına Binom Dağılımı denir.
Çekimlerin iadeli yapıldığı durumlarda x’in
gerçekleşme olasılıkları binom dağılı yardımı ile
elde edilmektedir. Hipergeometrik dağılım kesikli
bir tesadüfi değişkenin iadesiz çekimler sonucu
değişen
gerçekleşme
olasılıklarının
hesaplanmasında kullanılan bir dağılımdır.
Belirli bir zaman aralığında az sayıda gerçekleşen
tesadüfi olayların dağılımıdır. Bir makinenin bir
gün içerisinde arızalanma sayısı, bir haftada
ölümle biten trafik kazası sayısı vb. Poisson
dağılım gösteren tesadüfi değişkenlerdir.
Belirli bir aralıkta tam sayıları eşit olasılıklarla
alabilen tesadüfi değişkenler kesikli uniform
değişkenlerdir. N birimlik bir anakütleden çekilen
n birimlik örneklerin her birinin seçilme olasılıkları
süreksiz uniform dağılım gösterir.
İkiden fazla mümkün sonucun olduğu durumlarda
söz konusu olan bu dağılımın binom dağılımının
bir uzantısı olduğu söylenebilir. Çekim veya
deneylerde hep aynı olasılıklara sahip olan ikiden
fazla mümkün sonucun n birimlik örnekte
gerçekleme olasılıklarına mulnomial olasılık denir.
Formülü
Ortalaması
Varyansı
Standart
Sapması
x nPQ
P x (1 P)n x
E ( x) x nP
x2 E ( x x ) nPQ
k N k
x n x
p( N , n, k , x)
N
n
x nP n(k / N )
x2 nPQ
x x2
e x
p ( x)
x!
E ( x) x
x2
x
f ( x; n) 1/ n, x 1, 2,3...n
N!
1/
n !( N n)!
-
-
-
n!
P1n1 P2n2 ...Pknk
n1 !n2 !n3 !....nk !
-
-
-
N n
N 1
Dağılımın
Adı
Sürekli Olasılık Dağılımları
Normal
Dağılım
Standart
Normal
Dağılım
Açıklama
Aritmetik ortalamaya göre simetrik bir dağılım olan normal dağılım
ve değerlerine doğru yatay eksene asimptotik olarak
yaklaştığı için çan şeklinde bir eğri görünümündedir. Gauss
tarafından geliştirildiği için Gauss Eğrisi, tesadüfi hataların
dağılımına uyduğu için Tesadüfi Hatalar Eğrisi ve şeklinden dolayı
Çan Eğrisi adıyla da anılan Normal Eğri örnekleme teorisinin
temelini oluşturmaktadır.
Sürekli değişkenlerin dağılımı olan normal dağılım ve
arasında çok sayıdaki değerin olasılıklarından oluştuğu için her
değerin olasılığı çok küçüktür. Olasılıklar toplamı 1 olduğu için her
değerin çok küçük olasılığı yerine belirli aralıktaki değerlerin
olasılıkları hesaplanmaktadır. Bu nedenle olasılıklar tek bir değer
için değil bir grup şık için hesaplanmaktadır.
Formülü
1
f ( x)
e
2
Z
Ortalaması
Varyansı
Standart Sapması
-
-
-
-
-
-
-
-
-
-
-
-
( x x )2
2 2
xx
%68, 26 ' sı : x
%95 ' i : x 1,96
%95,5 ' i : x 2
%99 ' u : x 2,58
%99, 73' ü : x 3
Student(t)
Dağılımı
Üstel
Dağılım
Uniform
Dağılım
Örnek birim sayısının az olduğu durumlarda örnek ortalamalarının
gösterildiği dağılıma örnekleme teorisinde Student veya t Dağılımı
adı verilmektedir. Student dağılımı normal dağılım gibi simetrik
( 3 0) ancak normal dağılıma kıyasla daha basık ( 4 3) ve
değişkenliği daha fazla olan bir dağılımdır. t dağılımının basıklığı
serbestlik derecesine bağımlıdır.
Üstel dağılım Poisson sürecindeki birbirini takip eden olayların iki
zaman veya alan arasında gerçekleşme aralığının ölçümünde
kullanılan sürekli bir tesadüfi değişkenin olasılık dağılım
fonksiyonudur. Poisson dağılımında iki zaman veya alan aralığında
olayın gerçekleşme sayısı önem kazanırken üstel dağılımda bu
olaylardan herhangi ikisi arasındaki zaman veya alan aralığı önem
kazanmaktadır.
Belirli bir aralık içindeki her değerin gerçekleşme olasılığının eşit
olduğu bu tesadüfi değişkenin dağılımı Uniform Dağılımdır. Belirli
zaman aralığında düzenlenen tren, otobüs ve uçak seferlerinde
ulaşım araçlarının geliş zamanları tesadüfi değişkenin dağılımı
uniformdur.
f ( x) e x
x 0 ve 0
e 2, 71828
f ( x)
1
ba
0
a xb
aksi halde
x
ab
2
2
(b a)2
12
-
(b a) 2
12












