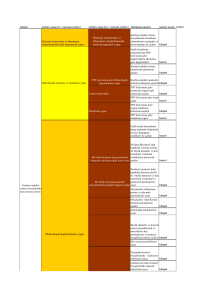
Ders slaytları : 80.251.40.59/veterinary.ankara.edu.tr/sgurcan İstatistik Herhangi bir konuyu incelemek amacıyla çalışmanın/araştırmaların planlanmasını, verilerin toplanmasını, değerlendirilmesini ve bir karara varılmasını sağlayan bilimdir. Biyoistatistik İstatistik alanında geliştirilen bilimsel yöntemleri Veteriner hekimlik, Tıp, diş hekimliği, eczacılık gibi alanlarda uygulamasını sağlayan bir bilim dalıdır. İstatistik konu olarak tanımlayıcı istatistik ve çıkarımsal istatistik olmak üzere iki ana gruba ayrılır. Tanımlayıcı istatistik: Elde edilen verilerin sınıflandırılması, ortalama ve yaygınlık ölçülerinin hesaplanması, tablo ve grafiklerle sunulmasını içerir. Çıkarımsal istatistik: Örneklemden elde edilen bulgular yardımıyla evren hakkında kestirimde bulunma, hipotezleri test etme ve karara varma gibi konuları içerir. Kitle (Evren) Araştırma kapsamına giren aynı özellikleri taşıyan birimlerin tümüne denir. Kitlenin büyüklüğü araştırmanın özelliğine göre değişir. Örneklem Bir kitleden, örnekleme yöntemlerinden yararlanarak seçilen aynı özellikleri taşıyan bir grup birimin oluşturduğu topluluğa denir. Örnekleme Evrenden örnek seçmek amacıyla geliştirilen çeşitli yöntemler vardır. Uygun yöntemlerle evrenden örneklem seçme işlemine “örnekleme” denir. Örnekleme Yöntemleri Olasılıksız Örnekleme Yöntemleri • Gönüllülerin İncelenmesi • Gelişigüzel Örnekleme • Kota Örneklemesi Olasılıklı Örnekleme Yöntemleri • • • • • Basit Rasgele Örnekleme Sistematik Örnekleme Tabakalı Rasgele Örnekleme Küme Örneklemesi Genişliğe Orantılı Örnekleme Parametre Evreni tanımlamak için kullanılan ölçülere parametre denir. İstatistik Örneklemi tanımlamak için kullanılan ölçülere istatistik denir. Evren ve Örneklem için Tanımlayıcı İstatistiklerin Gösterimi Tanımlayıcı Ölçüler Örneklem (İstatistik) Evren (Parametre) x µ Oran p P Standart Sapma S Varyans S2 2 Ortalama Standart Hata Gözlem Sayısı Sx n N Değişken Değişik değerler alan herhangi bir özelliğe değişken denir. Örneğin, boy uzunluğu, yaş, öğrenim düzeyi vb. kişiden kişiye değişen değerler olduğu için değişken olarak adlandırılır. Veri İncelenen konuya açıklık getirmek amacıyla toplanan bilgiler, belgeler, ölçümler, ... vb. Veri Tipleri Veriler genel olarak nitelik veriler ve sayısal veriler şeklinde iki gruba ayrılarak incelenirler. 1. Nitelik veriler Bireylerin sahip olduğu belli özelliklerin sınıflara ayrılarak belirtildiği verilerdir. Örneğin, cinsiyet, medeni durum, başarılı-başarısız gibi. Nitelik verilerde belli bir sıralama söz konusu ise (kötü-orta-iyimükemmel gibi) bu tür verilere sıralanabilir (ordinal) nitelik veriler denir. Böyle bir sıralama yoksa bu tür verilere sınıflanabilir (nominal) nitelik veriler denir. 2. Sayısal Veriler Sayısal veriler kesikli ve sürekli sayısal veriler olarak iki alt gruba ayrılır. Kesikli sayısal veriler, belirli bir aralıktaki tam sayıları alan veri türüdür. Örnek: Sınıftaki öğrenci sayısı, Sürekli sayısal veriler, ölçümle belirtilirler ve bir aralıktaki bütün değerleri alırlar. Örnek: Boy uzunluğu, vücut ağırlığı, günlük kalsiyum tüketim miktarı(mg) gibi. Nitelik Veriler ve Sayısal Veriler Arasındaki İlişki Hem kesikli sayısal veriler hem de sürekli sayısal veriler bazen nitelik veri olarak ifade edilebilirler. Örneğin sürekli sayısal bir veri olan canlı ağırlık kazancı verilerini 5 -9 10 – 14 15 – 19 Az verim Normal verim Yüksek verim Biçiminde sınıflandırarak nitelik veriye dönüştürebiliriz Verilerin Sınıflandırılması Eğer veri nitelik değişkense, kendiliğinden sınıflıdır. Örneğin yapılan bir araştırmada besi sonunda hayvanların vücut ağırlığına göre Zayıf Normal Yağlı Çok yağlı olarak sınıflandırıldığında Ağırlıkları nitelendiren bu veri kendiliğinden sınıflandırılmıştır. Araştırmacının amacı hayvanların vücut ağırlıklarına göre dağılımlarını incelemekse çeteleme işleminden yararlanılabilir. Çeteleme işlemleri için sınıflar alt alta yazılır ve ilk hayvandan başlamak üzere, araştırmaya katılan her bir hayvana ait olduğu vücut ağırlığının karşısına bir çetele atılır. Hayvanların Vücut Ağırlıklarına Göre Dağılımı Vücut Ağırlığı Zayıf Normal Yağlı Çok Yağlı Toplam Çetele Sayı % /////////////// 15 30 //////////////////// 20 40 ////////// 10 20 ///// 5 10 50 100 Sayısal Verilerin Sınıflandırılması Sayısal veriler için elde edilecek en kolay sınıflandırma, basit frekans dağılımlarının elde edilmesidir. Bunun için: veriler küçükten büyüğe (ya da büyükten küçüğe) doğru sıralanarak her bir gözlemden kaçar tane olduğu gözlemlerin karşısına yazılır. Beden Kitle İndeksi Sayı % 21,3 21,4 21,8 21,8 23,0 24,1 24,2 24,6 26,8 27,3 28,2 30,3 32,0 32,0 32,4 3,0 1,0 4,0 2,0 1,0 1,0 4,0 1,0 1,0 2,0 1,0 1,0 1,0 1,0 1,0 12,0 4,0 16,0 8,0 4,0 4,0 16,0 4,0 4,0 8,0 4,0 4,0 4,0 4,0 4,0 Toplam 25 100 Ancak dağılım aralığı (en büyük değerle en küçük değer arasındaki fark) büyüdükçe basit frekans dağılımları kullanışsızlaşır. Bu durum gözlem sayısının arttığı durumlarda daha da belirginleşir. Bu nedenle veriler sınıflandırılır. Sınıflandırma işlemlerinin belli adımları vardır. Sınıflandırmada kullanılan tanımlar: 1. Sınıf Sayısı: Oluşturulacak sınıf sayısıdır. Örnek: 50-54 55-59 60-64 65-69 70-74 Burada sınıf sayısı 5’tir 2. Sınıf Sınırı: Oluşturulacak her sınıfın bir alt ve bir üst sınırı vardır. Bu sınırlara sınıf sınırları denir. Örneğin 50-54 sınıfının alt sınırı 50 üst sınırı 54’tür. 3. Sınıf Aralığı (c): Ard arda gelen iki sınıfın üst sınırları ya da alt sınırları arasındaki farka sınıf aralığı denir. Yukarıdaki örnek için sınıf değeri= 2. Sınıfın alt sınır değeri ile 1. Sınıfın alt sınır değeri arasındaki fark 55-50=5’tir. 4. Sınıf Değeri: Her sınıfın alt ve üst sınır değerlerinin toplamının yarısıdır. Örneğin herhangi bir sınıfın alt sınırı 50 üst sınırı 54 ise Sınıf Değeri=(50+54)/2=52 5. Dağılım Aralığı: Dağılımdaki en büyük değerden en küçük değerin çıkartılması ile bulunur. Sınıflandırma İşleminde Dikkat Edilecek Noktalar Sınıflandırma sonucunda, dağılımdaki bütün değerler sınıflara dağıtılabilmeli ve hiçbir değer sınıflama dışında kalmamalıdır. Örneğin beden kitle indeksi verileri 20-25 26-30 31-35 biçiminde olsaydı sınıflandırma işlemi yanlış olurdu. Çünkü 25-26 ve 30-31 arasında değerler varsa bu gözlemlerin hangi sınıfta yer alacağı belli değildir ve sınıflama yapıldığında bu değerler dışarıda kalır. Eğer virgülden sonra basamak varsa sınıflama işlemi yapılırken virgülden sonraki haneler dikkate alınmalıdır. Örneğin bu sınıflandırma aşağıdaki gibi yapılabilir. 20,0-24,9 25,0-29,9 30,0-34,9 Sınıflama yaparken sınıflar birbirinin içine girmemelidir. Örneğin sınıfları 50-54 54-59 59-64 biçiminde oluşturmak hatalıdır. Çünkü 54 ve 59 değerleri iki ayrı sınıfta yer almaktadır. Doğru olanı 50-54 55-59 60-64 olmalıdır. Sınıf aralıklarının birbirine eşit şekilde düzenlenmesi, istatistiksel çözümlemede kolaylık sağlar. Ancak gerektiğinde sınıf aralıkları eşit olmayabilir. Dağılım hakkında yeterli bilgiye sahip olabilmek için oluşturulacak sınıf sayısının 8-15 arasında olması önerilmektedir. Sınıf sayısının az olması dağılım hakkında ayrıntılı bilgi elde etmemize engel olur. Örnek : Daha önce Beden Kitle İndeksi verilen 25 kişinin verilerini sınıflandıralım BKİ verinde En Küçük Değer (EKD)=21.3 En Büyük Değer (EBD)=32.4 ‘tür Dağılım Aralığı (DA) bulunur. Bu örnek için DA = EBD-EKD = 11.1’dir. Dağılım aralığı değeri belirlediğimiz sınıf sayısına bölünerek sınıf aralığı (C) bulunur. Örneğin veriyi 4 sınıfta toplamak istersek C=11,1/4=2,75 3 olur. (Sonuç tamsayı olacağı için yuvarlama yapılır). Buna Göre sınıflar, dağılımdaki en küçük değerden başlamak üzere aşağıdaki gibi oluşturulur. EKD 21,3 24,3 27,3 30,3 EBD 24,2 27,2 30,2 33,2 Daha sonra her sınıfa düşen frekanslar 1 no’lu kişiden başlamak üzere çeteleme yapılır ve sayısı yazılır. BKİ 21,3 24,3 27,3 30,3 24,2 27,2 30,2 33,2 Çetele Sayı //////////////// // /// //// 16 2 3 4 BKİ 21,3 24,2 24,3 27,2 27,3 30,2 30,3 33,2 Toplam Frekans (Sayı) 16 2 3 4 25 % 64.0 8.0 12.0 16.0 100.0 Yığılımlı Frekans 16 18 21 25 Yığılımlı % 64.0 72.0 84.0 100.0 Sınıflandırma Örneği sy 9 75 çocuğun boy uzunlukları ölçülmüş, veriler doğrultusunda sınıflandırma örneği Max=115 Min=90 DA=115-90=25 25/15<c<25/8 1,7<c<3,1 115 94 110 103 92 104 114 106 100 102 113 98 101 99 103 93 107 96 113 110 90 100 103 114 111 105 99 102 98 97 114 108 103 100 98 101 104 110 114 113 105 103 111 109 112 104 104 102 107 106 94 96 101 101 106 107 105 113 112 99 100 95 97 108 102 104 93 91 99 109 108 106 109 105 96 Çocukların Boy Uzunluğuna İlişkin Frekans Tablosu Sınıflar Çetele 90-92 /// 3 93-95 ///// 5 96-98 ///// /// 8 99-101 ///// ///// // 12 102-104 ///// ///// //// 14 105-107 ///// ///// / 11 108-110 ///// //// 9 111-113 ///// /// 8 114-116 ///// 5 Toplam Frekans 75