PowerPoint Sunusu

HAZIRLAYAN: KÜBRA NUR UÇAN
120403009
2/A
İÇİNDEKİLER

 ÜÇGENİN TANIMI
 ÜÇGENLERLE İLGİLİ KAVRAMLAR
 ÜÇGEN ÇEŞİTLERİ
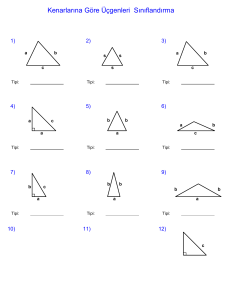
 KENARLARINA GÖRE ÜÇGENLER
EŞKENAR ÜÇGEN
İKİZKENAR ÜÇGEN
ÇEŞİTKENAR ÜÇGEN
 AÇILARINA GÖRE ÜÇGENLER
DAR AÇILI ÜÇGEN
GENİŞ AÇILI ÜÇGEN
DİK ÜÇGEN
 ÖRNEKLER
 ÇÖZÜMLER
 KAZANIMLAR
 KAYNAKÇALAR
ÜÇGENLER

 TANIM: Üçgen; doğrusal olmayan üç noktayı ikişer
ikişer birleştiren doğru parçalarının birle
ÜÇGENLER

ÜÇGENLERLE İLGİLİ
KAVRAMLAR

 Üçgenin iç açıları toplamı 180 dir.
 Üçgenin dış açıları toplamı 360 dir.
ÜÇGENLER

 Üçgende bir dış açının ölçüsü kendisine komşu
olmayan iki iç açının toplamına eşittir.
ÜÇGEN
ÇEŞİTLERİ

Üçgen kenarlarına ve açılarına göre çeşitlere ayrılır.
KENARLARINA GÖRE:
Eşkenar
üçgen
İkizkenar
üçgen
Çeşitkenar
üçgen
AÇILARINA GÖRE:

A
A<90

A=90
A>90

A


EŞKENAR ÜÇGEN

Bütün kenarlarının uzunlukları eşit olan üçgene eşkenar üçgen
denir.

İKİZKENAR ÜÇGEN
İki kenarının uzunlukları eşit olan üçgene ikizkenar üçgen denir.

ÇEŞİTKENAR ÜÇGEN
Üç kenarının uzunlukları birbirlerinden farklı olan üçgene
çeşitkenar üçgen denir.

 DAR AÇILI ÜÇGEN
İç açılarının her biri 90 dereceden küçük olan üçgene dar açılı
üçgen denir.
 DİK AÇILI ÜÇGEN
Bir iç açısı 90 derece olan üçgene dik açılı üçgen veya dik üçgen
denir. Dik üçgende dik açının karşısındaki kenara hipotenüs, diğer
iki kenara da dikkenar adı verilir.
 GENİŞ AÇILI ÜÇGEN
Bir iç açısı 90 dereceden büyük olan üçgene geniş açılı üçgen
denir.
ÖRNEKLER

ÇÖZÜM


KAZANIMLAR

 Terimler: Hipotenüs, Pisagor bağıntısı, üçgen eşitsizliği, dik
kenarlar, kenarortay, açıortay, yükseklik
 Üçgende kenarortay, açıortay ve yüksekliği inşa eder.
Kâğıtları katlayarak, keserek veya kareli kâğıt üzerinde çizim
yaparak üçgenin elemanlarını oluşturmaya yönelik çalışmalara yer
verilir.
Eşkenar, ikizkenar ve dik üçgen gibi özel üçgenlerde
kenarortay, açıortay ve yüksekliğin özelliklerini belirlemeye
yönelik çalışmalara da yer verilir.

 Üçgenin iki kenar uzunluğunun toplamı veya farkı ile
üçüncü kenarının uzunluğunu ilişkilendirir.
Somut modeller kullanılarak yapılacak etkinliklere yer
verilebilir. Uygun bilgisayar yazılımları ile üçgen eşitsizliğini
anlamaya yönelik çalışmalara yer verilebilir.
 Üçgenin kenar uzunlukları ile bu kenarların karşısındaki
açıların ölçülerini ilişkilendirir.
Dik üçgende dik kenarlar ve hipotenüs tanıtılıp açı
ölçüleriyle kenar uzunlukları arasındaki ilişki de ele alınır.

 Yeterli sayıda elemanının ölçüleri verilen bir üçgeni çizer.
(1) Üç kenarının uzunluğu, (2) bir kenarının uzunluğu ile iki
açısının ölçüsü, (3)iki kenar uzunluğu ile bu kenarların arasındaki
açının ölçüsü verilen üçgenlerin uygun araçlar kullanılarak
çizilmesi sağlanır. Dinamik geometri yazılımları ile yapılacak
çalışmalara yer verilebilir.
 Pisagor bağıntısını oluşturur; ilgili problemleri çözer.
Pisagor bağıntısının gerçek yaşam uygulamalarına yönelik
çalışmalara yer verilir. Koordinat düzlemi üzerinde verilen iki
nokta arasındaki uzaklığı Pisagor bağıntısını kullanarak bulma
çalışmalarına yer verilir. Kenar uzunlukları verilen bir üçgenin dik
üçgen olup olmadığına Pisagor bağıntısını kullanarak karar
vermeye yönelik çalışmalar yapılır.
KAYNAKÇALAR

 SANALOKULUMUZ.COM
 TESTİMİZ .COM
 MATEMATİKCİFATİH.COM
 BİLGİCİK.COM
