basit makinalar

Özet
BASİT MAKİNALAR
Basit Makineler Yaşamımızı Kolaylaştırır
Günlük yaşantımızda işlerimizi kolaylaştırmak için kullandığımız, bir ya da iki parçadan oluşan araçlara basit
makineler denir. Basit makineler, iş ya da enerjiden bir kazanç sağlamazlar. Sürtünmeleri ihmal ettiğimizde,
basit makineyle yapılan iş, yükün kazandığı enerjiye eşittir. Basit makineler, kuvvetin doğrultusunu, yönünü
ya da büyüklüğünü değiştirmek için kullanılır.
Basit makinelerin temel prensipleri,
1. Kuvvetten kazanç varsa ayni oranda yoldan kayıp olur.
2. Yoldan kazanç varsa, ayni oranda kuvvetten kayıp olur.
3. Basit makineler iş veya enerjiden asla kazanç sağlamaz.
Başlıca basit makineler şunlardır; kaldıraçlar, makaralar, palangalar, çıkrık, eğik düzlem, vida, kama, dişli
çarklar ve tekerleklerdir.
Kaldıraçlar: Sabit bir destek etrafında hareket edebilen sağlam çubuklara kaldıraç denir.
Kaldıracın etrafında döndüğü noktaya destek denir. Uygulanan kuvvetin destek noktasına olan uzaklığa
kuvvet kolu, yük ile destek arasındaki uzaklığa yük kolu denir. Bir kaldıraçta kuvvet kolu, yük kolundan ne
kadar uzun olursa, bu kaldıraçla kaldırılabilecek yük de o kadar büyük olur.
Şekildeki gibi denge durumundaki bir kaldıraçta kuvvetle kuvvet kolunun çarpımı, yükle yük kolunun
çarpımına eşittir. Buna kaldıraç bağıntısı denir.
Kuvvet x Kuvvet kolu = Yük x Yük kolu
Bunu sembolle gösterirsek,
F x |AO| = P x |OB|
Kaldıraçlar, destek noktasının bulunduğu yere göre çift taraflı ve tek taraflı kaldıraç olmak üzere iki gruba
ayrılır.
1. Çift Taraflı Kaldıraç
Desteğin ortada olduğu kaldıraçlara denir. Kuvvetin yönünü değiştirir, kuvvetten kazanç sağlar.
1
Günlük hayatta çift taraflı kaldıraca benzer pek çok araç kullanırız. Örneğin makas, pense, eşit kollu terazi,
levye, kayık küreği, tahterevalli desteğin ortada olduğu kaldıraca benzer araçlardır.
2. Tek Taraflı Kaldıraç
Desteğin uçta olduğu kaldıraçtır. İki çeşittir:
a. Desteğin uçta, yükün ortada olduğu kaldıraç. Kuvvetten kazanç, yoldan kayıp vardır.
Desteğin uçta, yükün ortada olduğu kaldıraçlara örnekler; el arabası, fındık kıracağı, gazoz açacağı, çenemiz.
2
2 b. Desteğin uçta, kuvvetin ortada olduğu kaldıraç. Yoldan kazanç, kuvvetten kayıp vardır.
Bu çeşit kaldıraca örnekler; cımbız, maşa, iş makinelerinin pistonla çalışan kolları, ön kollarımız.
Kuvvet Kazancı: Basit makinelerde kuvvet kazancı, yükün kuvvete oranı olarak ifade edilir.
yük x yük kolu = kuvvet x kuvvet kolu olduğuna göre,
yazılabilir.
Kuvvet kazancı = Yük / Kuvvet = Yük kolu / Kuvvet kolu
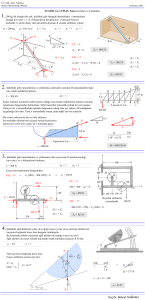
ÖRNEK: Şekildeki düzenekte yükü dengeleyen kuvvet kaç N’dur?
ÖRNEK: Aşağıdaki sistemleri dengeye getirmek için okla gösterilen noktalara kuvvetler uygulanmaktadır.
Hangi kuvvet en büyüktür?
3
ÖRNEK: Şekildeki sistem dengededir. Çubuğun
ağırlığı
ihmal edilmiştir.
Sistemi dengede tutan F kuvveti kaç N’dur?
Kuvvet kazancı kaçtır?
ÖRNEK:
Şekildeki gibi eşit bölmelendirilmiş homojen bir
çubuk,bir iple tavana asılarak dengelenmiştir.
Çubuğun ağırlığı 50 N olduğuna göre, ipteki
gerilme kaç N’dur?
Özet
MAKARALAR
Üzerinde ipin geçebileceği oluk bulunan, sabit bir eksen etrafında serbestçe
dönebilen disk şeklinde bir araçtır.
Makaralar, kullanış şekline göre sabit ve hareketli olmak üzere iki çeşittir.
1. Sabit Makara
Dönme ekseni bir yere sabitlenmiş makaradır. İp makara üzerinden geçirilir
ve ucuna yük asılır. İp diğer ucundan çekilince yük kaldırılır. Sabit makara
sadece kuvvetin yönünü değiştirir, kuvvetten ya da yoldan kazanç sağlamaz.
Sürtünmeler ihmal edilirse kuvvet, yüke eşittir.
2. Hareketli Makara
Dönme ekseni bir çengelle yüke bağlanmış, yükle beraber hareket eden
makaradır.
Sürtünmeler ihmal edilirse, hareketli makarada kuvvet yükün yarısına eşittir.
4
ÖRNEK: Şekildeki sistemde, 10 N’luk P yükünü dengeleyen F kuvveti
kaç N’dur? (Ipin ve makaranın ağırlığı ile sürtünme ihmal edilecek)
Palangalar
Sabit ve hareketli makaraların birlikte kullanılmasıyla oluşturulmuş sisteme
palanga denir. Palangada kuvvetten büyük oranda kazanç vardır. Fakat
aynı oranda yoldan kayıp vardır.
ÖRNEK:
Şekildeki sistemde makaralar ağırlıksızdır.
Sistem sürtünmesizdir.
a. Yükü dengeleyen kuvvet kaç N’dur?
b. Yükü 10 m kaldırmak için ip kaç m çekilmelidir?
c. Kuvvet kazancı nedir?
*****Makaralar ve palangalar, iş makinelerinde gemilerde, yük kaldırma makinelerinde kullanılır.
*****Bayrak direğinin üst tarafında sabit makara bulunur.
ÖRNEK: Şekildeki sistemde 400 N’luk kuvvetle kaç N’luk yük
dengelenebilir?
ÖRNEK: Şekildeki sistemde yükü
20 m kaldırmak için ipin kaç m
çekilmesi
gerekir?
5
Özet
MERKEZLERİ FARKLI OLAN MAKARALAR
Merkezleri farklı olan makaralarda kuvveti birinden
diğerine aktarmak için zincir ya da kayış kullanılır.
Şekildeki makaralar için;
büyük makaranın dönme sayısı = n1
küçük makaranın dönme sayısı = n2
büyük makaranın yarıçapı = r1
küçük makaranın yarıçapı = r2
Kayışlar çapraz takılarak makaraların dönme yönleri
değiştirilebilir.
Eğik Düzlem
Bir ucu diğer ucundan daha yüksekte olan
düzlemlere
eğik düzlem denir.
Eğik düzlem kullanılarak, çok büyük ağırlıklar,
küçük
kuvvetlerle kaldırılabilir.
Dağlara çıkan kıvrımlı yollar, yürüyen
merdivenler, yükleme rampaları, yükleme kalası,
eğik düzleme örnek olarak verilebilir.
Bu şekilde P yükü, F kuvveti, L kuvvet yolunu, h
yük kolunu göstermektedir.
Eğik düzlemde, sürtünmeler ihmal edilirse, yükün
yaptığı iş, kuvvetin yaptığı işe eşittir.
Kuvvet x kuvvet yolu = Yük x Yük yolu
FxL=Pxh
F/P = h/L F = P.h / L
Bu formülden görülebileceği gibi, eğik düzlem ne kadar uzun olursa, yükü çeken kuvvet o kadar az olur. Ayrıca,
eğik düzlemin yüksekliği ne kadar az olursa, yükü çeken kuvvet de o kadar az olur.
6
ÖRNEK:
Şekildeki eğik düzlemde AB = 6 m, BC = 2 m olduğuna göre
240 N’luk P yükünü hareket ettirmek için en az kaç N’luk F
kuvveti uygulanmalıdır? (Sürtünme önemsenmeyecek)
Çıkrık
Yarıçapları birbirinden farklı, dönme eksenleri aynı, birbirine
sabitlenmiş iki silindirden oluşan bir sistemdir.
Çıkrık, çift taraflı kaldıraca benzer.
Sürtünmelerin ihmal edildiği bir çıkrık için şu bağıntı yazılabilir:
FxR=Pxr
Motorla çalışan makinelerin çoğunda çıkrık sistemi vardır.
Çevremizde çıkrığa benzer birçok araç gereç bulunur.
Tornavida, anahtar, kapı kolu, pencere kolu, musluk başı,
bisikletlerin pedal sistemi, vana başları, araba
direksiyonu, el mikseri, el matkabı, kahve değirmeni
çıkrık prensibine göre çalışır.
Dişli Çarklar
Dişli çarklar, üzerinde eşit aralıklarla açılmış dişlerin bulunduğu, sabit bir eksen etrafında dönebilen silindir
şeklindeki yapılardır. Silindir üzerindeki dişler, çarkların birbirine geçmesine yarar. Dişler, bir çark üzerine
uygulanan kuvveti
diğer çarklara aktarır. Dişli çarklar hareketin yönünü ve hızını değiştirmeye
yarar.
Birbirine değen dişlilerin dönme yönleri terstir.
Şekildeki birbirine değen dişliler için;
büyük dişlinin dönme sayısı = n1
küçük dişlinin dönme sayısı = n2
büyük dişlinin diş sayısı = r1
küçük dişlinin diş sayısı = r2
n1 / n2 = r1 / r2
Vida
Vida, silindirle eğik düzlemin birleşmiş bir şekli gibi düşünülebilir. Vida, bir silindir
üzerinde spiral şeklinde açılmış oyuklardan oluşur.
Vida ile çok büyük sıkıştırıcı ya da delici kuvvetler elde edilebilir. Çok büyük
oranlarda kuvvetten kazanç sağlanabilir.
FÇ = vidayı çeviren kuvvet
R = vidayı döndüren kuvvetin dönme eksenine uzaklığı
a= vida adımı
FD = delici kuvvet
Vidayı çeviren kuvvet, R yarıçaplı bir dairenin çevresini dolanır. Bu durumda çevirici kuvvetin yaptığı iş, delici
kuvvetin yaptığı işe eşit olur.
ÖRNEK:
Yanda görülen vidayı çeviren kuvvet kolu 30 N’luk bir kuvvetle
çevrildiğinde,
vidanın oluşturacağı sıkıştırma kuvveti kaç N’dur?(ğ = 3 alınız)
7
Kama
Cisimleri delmek, kesmek, parçalamak ya da kaldırmak için kullanılan iki yüzü eğimli
basit bir makinedir. Kamalar, genelde demir ya da çelikten yapılır. Ucu sivri eğik
düzlem şeklinde bir alettir. Iğne, bıcak, jilet, keski, makasın ağzı, keser, balta, kamaya
benzer aletlerdir.
Kama kuvvetin yönünü değiştirir.
Kama, yoldan kaybettirir, kuvvetten kazandırır.
Tekerlek
Bir milin etrafında, serbestçe dönebilen disk şeklinde bir araçtır. Tekerlekler,
üzerinde taşıdıkları cisimle zemin arasındaki sürtünmeyi azaltırlar.Tekerlek, karada
giden taşıtlarda, el arabalarında, çocuk arabalarında ve hareketli birçok sistemde
kullanılır.
8