5. Uluslararası İleri Teknolojiler Sempozyumu (IATS’09), 13-15 Mayıs 2009, Karabük, Türkiye
SIKIŞTIRILAMAZ BİR AKIŞTA GEÇİRGEN BİR YÜZEYDEN YAPILAN
YAYILI ÜFLEMENİN ISI GEÇİŞİ ÜZERİNDEKİ ETKİSİNİN İNCELENMESİ
AN ANALYSIS OF THE EFFECT OF UNIFORM INJECTION THROUGH A
POROUS SURFACE ON HEAT TRANSFER
IN A INCOMPRESSIBLE FLOW
a, *
a, *
Osman TURAN
b
ve Burhan ÇUHADAROĞLU
KTÜ Makine Mühendisliği Bölümü, Trabzon, Türkiye, E-posta: osmanturan@ktu.edu.tr
b
KTÜ Makine Mühendisliği Bölümü, Trabzon, Türkiye, E-posta: burhan@ktu.edu.tr
Özet
Bu çalışmada; geçirgen ve sabit yüzey sıcaklığına sahip
düzlem levha üzerindeki gelişmiş sınır tabaka akışında
hidrodinamik ve ısıl duvar fonksiyonları teorik olarak elde
edilmiş, üfleme-emme hızı ve viskoz yutulmanın boyutsuz
sıcaklık üzerindeki etkisi analitik olarak incelenmiştir.
Çalışmada viskoz yutulmanın etkisi Brinkman sayısının
farklı bir şekli olan boyutsuz B = uτ 3 ρ / qw sayısı ile
tanımlanmıştır. Sınır tabaka içerisindeki boyutsuz sıcaklık
dağılımının, viskoz yutulma ve yüzeyden yapılan üflemeemme uygulamasından önemli ölçüde etkilendiği
belirlenmiştir. Çeşitli teknolojik uygulamalarda karşılaşılan
viskoz yutulma kaynaklı ısı üretiminin, yüzeyden yapılan
üfleme-emme uygulaması ile denetim altına alınabileceği
görülmüştür.
Anahtar kelimeler: Viskoz yutulma, üfleme, emme, sınır
tabaka, duvar fonksiyonu
Abstract
In the present study; the hydrodynamic and the thermal
wall functions on a permeable wall with constant
temperature in the boundary layer flow were obtained
theoretically and the effect of injection-suction velocity and
the viscous dissipation on the dimensionless temperature
was investigated. The effect of viscous dissipation was
defined as a dimensionless number of B = uτ 3 ρ / qw which
is a modified Brinkman number. It was noted that the
dimensionless temperature distribution in the thermal
boundary layer was substantially influenced by the viscous
dissipation and the injection-suction through permeable
wall. In addition, It was seen that the viscous heating which
appears in some technological applications can be
controlled by the injection-suction through permeable wall.
Keywords: Viscous dissipation,
boundary layer, wall function
injection,
suction,
1. Giriş
Günümüzde; geçirgen bir yüzey üzerindeki türbülanslı
akışın incelenmesi akışkanlar mekaniği ve ısı transferinin
ilgi çeken konuları arasında yer almaktadır. Bilindiği üzere;
cisimler etrafındaki akışta ortaya çıkan sınır tabakanın
denetimi için birçok yöntem uygulanmaktadır. Yüzeyden
üfleme-emme yapılarak hidrodinamik ve ısıl sınır
© IATS’09, Karabük Üniversitesi, Karabük, Türkiye
tabakanın denetimi, uçak kanadı etrafındaki akışın kontrolü
ve elektronik donanımların soğutulması gibi çeşitli
mühendislik uygulamalarında kullanılmaktadır. Sınır
tabakaya yüzeyden yapılan üfleme ile akışa momentum ve
ısı transferi yapılmakta ve bu sayede akışın istenilen
yapıya
dönüştürülmesi
amaçlanmaktadır.
Örneğin;
geçirgen yüzeyli bir cisim üzerinden yapılan üfleme ile
akışın momentum dengesi değiştirilerek, cisim üzerindeki
direnç kuvvetini belirli ölçüde denetim altına alma olanağı
vardır. Üfleme uygulaması ayrıca, film soğutma sağlayarak
uzay taşıtları ve gaz türbin kanatçıkları gibi yüksek hızlı
sistemlerde ortaya çıkan aşırı ısınma problemini belirli
ölçüde çözmede kullanılmaktadır. Emme uygulaması ise;
cisim üzerinden sınır tabaka ayrılmasını geciktirerek
basınç farkı kaynaklı direncin düşürülmesi konusunda
yardımcı olmaktadır. Ayrıca yüzeyden yapılan yayılı emme
ile küçülen sınır tabaka kalınlığına bağlı olarak ısı
geçişinde önemli ölçüde artışlar ortaya çıkmaktadır.
Geçirgen bir yüzey üzerinden yapılan üfleme veya emme
ile sınır tabakanın denetlenmesi konusundaki temel
teknikler ve konunun matematiksel esasları Schlichting ve
Gersten’de [1] verilmiştir. Bu kaynakta; geçirgen yüzey
üzerindeki üfleme veya emmeli laminer sınır tabakanın
belirli sınır koşulları altında yapılmış baz analitik çözümleri
verilmiştir. Burada hız ve sıcaklık profilleri formüle edilmiş
ve sürekli emme-üflemeli yatay düz levhadan olan ısı
geçişi incelenmiştir. Sumitani ve Kasagi [2] karşılıklı
üflemeli ve emmeli yüzeylere sahip bir kanal için
“Doğrudan Sayısal Benzeşim (DNS)” yöntemi ile yapmış
oldukları sayısal incelemede, üflemenin hız ve sıcaklık
çalkantılarını, Reynolds kayma gerilmelerini ve türbülanslı
ısı akılarını artırmakta olduğunu, emmenin ise azaltmakta
olduğunu göstermişlerdir. Bellettre ve diğ. [3] artan üfleme
debisine bağlı olarak sürtünme faktörü ve ısı geçişinin
önemli ölçüde düşmekte olduğunu gözlemişlerdir. Bu
çalışmanın sonuçları deneysel veriler ile kıyaslanmış ve iyi
bir uyum elde edilmiştir. Hwang ve Lin [4] geçirgen duvarlı
bir kanal akışında belirli bir türbülans modeli kullanarak
dinamik ve ısıl alanlar için sayısal bir inceleme yapmışlar
ve iyi bir uyum elde etmişlerdir. Meinert ve diğ. [5]
geçirgen bir duvardan türbülanslı bir akışa farklı bir gaz ile
yapılan üflemenin duvar ve akış arasındaki ıs geçişi
üzerinde önemli bir etkisi olduğunu göstermişlerdir.
Çuhadaroğlu [6] yüzeyden belirli bir açı ile yapılan üfleme
veya emmenin türbülanslı sınır tabaka üzerindeki etkilerini
sayısal olarak incelemiştir. Bu çalışmaya göre; yerel
sürtünme katsayısı ve ısıl sınır tabaka kalınlığı üfleme hızı
ve açısından önemli bir şekilde etkilenmektedir.
Turan. O.. ve Çuhadaroğlu. B.
Bu çalışmanın amacı; geçirgen yüzeyli düzlem levha
üzerindeki türbülanslı sınır tabaka akışında viskoz alt
tabakaya ait duvar fonksiyonları üzerinde üfleme-emmenin
ve viskoz yutulmanın etkisini analitik olarak incelemektir.
v
2. Teorik Çalışma
Geçirgen bir yüzey üzerindeki iki boyutlu sıkıştırılamaz ve
sıfır basınç gradyanlı sınır tabaka akışında duvar
fonksiyonlarını
elde
etmek
üzere
momentum
denkleminden yola çıkılacak olursa .
u
sıkıştırılamaz sınır tabaka akışında viskoz
etkisinin de dikkate alındığı enerji denklemi
∂u
∂u ∂ ∂u
υ
+v
=
∂x
∂y ∂y ∂y
(1)
v
du d du
υ
=
dy dy dy
(2)
şekline dönüşür. (2) denkleminin y=0’dan herhangi bir y
noktasına kadar aşağıdaki sınır koşulları için integrali
alınırsa;
v( 0 ) = V w
υ
du
dy
=
y =0
(3.a)
τw
= uτ 2
ρ
uτ 2 = υ
du
− uV w
dy
denklemi
elde
(3.b)
gösteren Φ = ( du / dy )2 olarak dikkate alınmıştır. (7)
denkleminin geçirgen yüzey için (3) ile verilen sınır
koşulları ve ısıl büyüklükler için aşağıda ifade edilen
koşullar altında y=0’dan herhangi bir y mesafesine kadar
integrali alınırsa;
= Tw
dT
dy
y =0
edilir.
Bu
denklem
V w (T − Tw ) + q w /ρ c p −
dT
=
dy
dT +
dy +
υ
Pr
(9)
y + du +
+
1 + Vw T − B ∫
+
0 dy
=
1
Pr
2
dy +
(10)
olarak sınır tabakadaki boyutsuz sıcaklık gradyanı elde
edilir. Bu ifadede yer alan B boyutsuz sayısı
B=
exp(
y du 2
∫ dy
dy
y =0
Bu denklem T + = ( T − Tw )( ρ c p u z ) / qw boyutsuz sıcaklık
boyutsuz hız gradyanı elde edilir. Bu ifadenin y =0’dan
+
herhangi bir boyutsuz y değerine kadar integrali alınırsa;
u+ =
υ
cp
(5)
+
y V w+
V w+
(8.b)
= qw
sınır tabaka boyunca sıcaklık gradyanı elde edilir;
u + = u / uτ
= 1 + u +V w+
+
(8.a)
tanımı kullanılarak boyutsuzlaştırılırsa;
ve
y + = yuτ / υ
boyutsuzlaştırma
parametreleri kullanılarak boyutsuzlaştırılacak olursa:
dy +
k
y =0
(4)
V w + = V w / uτ
du +
(7)
şeklinde ifade edilir. Bu denklemde viskoz yutulma etkisini
T
Duvar yakınında ∂u / ∂x türevi küçük değerler alacağı için
göz ardı edilirse momentum denklemi;
dT
d k dT υ
=
+
Φ
dy dy ρ c p dy c p
yutulma
) −1
uτ 3 ρ
qw
(11)
(6)
yüzeyden üfleme veya emme yapılan sınır tabaka için
boyutsuz hız dağılımını veren duvar fonksiyonu elde edilir.
Üstel yapıda olan bu bağıntı geçirgen olmayan yüzey için
V w+ = 0 yazıldığında laminer sınır tabaka için geçerli olan
u + = y + şekline dönüşür.
Geçirgen yüzeyden yapılan üfleme veya emmenin ısıl
sınır tabaka üzerindeki etkisi hidrodinamik sınır tabaka
üzerindeki etkisine oldukça benzerdir [6]. Sabit yüzey
sıcaklığına sahip geçirgen bir yüzey üzerindeki iki boyutlu
şeklinde
tanımlanmış
olup,
viskoz
sürtünmeden
kaynaklanan ısı üretiminin bir ölçüsünü ifade etmektedir.
Boyutsuz B sayısı viskoz kaynaklı ısı üretiminin yüzeydeki
ısı iletimine olan oranını ifade eden ve Br = µu ∞2 /( k∆T )
şeklinde tanımlanan Brinkman sayısının farklı bir formda
yazılmış şeklidir. Pr; Prandtl sayısına karşılık gelmekte
olup, burada standart koşullardaki hava için 0,7 olarak göz
önüne alınmıştır. Bu bağıntıdaki boyutsuz hız gradyanı için
verilmiş olan (6) eşitliğinin yerine yazılması ve elde edilen
+
+
bağıntının y =0’dan herhangi bir y değerine kadar integre
edilmesi ile;
Turan. O.. ve Çuhadaroğlu. B.
T+ =
(
+
exp Pr V w y +
Vw
+
(
)+
B
2V w
)
+2
(
)
Pr exp 2V w + y + 2 exp Pr V w + y +
×
−
− 1
Pr − 2
Pr − 2
(12)
davranışı; yüzeydeki ısı akısındaki artışın, sıcaklık farkına
(T-Tw)
oranla
daha
fazla
olmaya
başladığını
+
göstermektedir. Diğer bir deyişle T ‘da ortaya çıkan
düşme, yüzey yakınındaki viskoz yutulma nedeniyle
akışkandan yüzeye olan qw ısı akısında ortaya çıkan
artışın, sıcaklıktaki artıştan daha fazla olmasından
kaynaklanmaktadır.
ısıl sınır tabaka boyunca boyutsuz sıcaklık için üflemeemme ve viskoz yutulma etkisini içeren duvar fonksiyonu
elde edilir. V w+ = 0 özel durumunda bu bağıntı hız için elde
edilmiş olan duvar fonksiyonuna benzer şekilde bilinen
T + = Pr . y + bağıntısına dönüşür. (12) ile tanımlanmış
olan boyutsuz sıcaklık, V w+ , y + boyutsuz parametrelerinin
yanı sıra, viskoz yutulmanın bir ölçüsü olan B sayısına da
bağlıdır. Bu çalışmada sınır tabaka içerisindeki boyutsuz
sıcaklığın V w+ üfleme-emme hızının yanı sıra B ile olan
ilişkisi de incelenmiştir.
3. Bulgular
Bu çalışmada geçirgen yüzeyli ve sabit yüzey sıcaklığına
sahip bir düzlem levha üzerindeki akışta ortaya çıkan sınır
tabakada (Şekil 1), üfleme-emmenin ve viskoz yutulmanın
sıcaklık dağılımı üzerindeki etkisi analitik olarak
incelenmiştir. Viskoz yutulma sıcaklık dağılımını önemli
ölçüde etkileyen bir iç ısı kaynağıdır. Bu çalışmada
boyutsuz üfleme-emme hızının yanı sıra, viskoz yutulma
ile sıcaklık dağılımı arasındaki oransal ilişki için
tanımlanmış olan B sayısı da temel parametre olarak göz
önüne alınmıştır.
Şekil 2. Üflemesiz-emmesiz ( Vw+ = 0 ) durumda viskoz
yutulmanın boyutsuz sıcaklık üzerindeki etkisi.
Bkr değerinden daha yüksek değere sahip viskoz
yutulmanın
olduğu
durumlarda,
yüzeyden
belirli
uzaklıklarda boyutsuz sıcaklık negatif değerler almaya
başlamaktadır (Şekil 2). Yüzeydeki akışkan sıcaklığının,
akışkan sıcaklığının üzerine çıkması (Tw,f>T) anlamına
gelen bu davranış viskoz yutulmanın yüzeydeki akışkan
sıcaklığı üzerindeki etkisinden kaynaklanmaktadır. Bkr
değerinin üzerine çıkıldığında viskoz yutulma kaynaklı iç
ısı üretimi nedeni ile yüzeydeki akışkan sıcaklığında
sıçrama meydana gelerek buradaki akışkan sıcaklığı hem
duvar hem de cidardan uzaktaki akışkanın sıcaklığının
üzerine çıkmaktadır.
Şekil 1. Geçirgen yüzey üzerinde üfleme ve sınır tabakalar
Yüzeyden olan boyutsuz uzaklık ve boyutsuz sıcaklık için
(12) bağıntısı ile verilmiş olan analitik ilişkiye ait farklı B
değerlerindeki değişimler, geçirgen olmayan yüzey
( V w+ = 0 ) durumunda, Şekil 2’de görülmektedir. Burada da
görüldüğü gibi; belirli bir Bkr değeri için (şekilde Bkr=0,1
olarak görülmektedir) yüzeyden uzaklaşıldıkça boyutsuz
sıcaklıktaki değişim azalmakta ve nihayet yüzeyden
itibaren belirli bir y kr+ değerinde değişim durmakta, daha
yüksek y + değerlerinde ise boyutsuz sıcaklık düşme
davranışı göstermektedir. Yüzey yakınında viskoz yutulma
etkisinin artması ile doğal olarak bu bölgede sıcaklık farkı
da (T-Tw) artmaktadır. Buna bağlı olarak da akışkandan
yüzeye geçen ısı akısı artar. Yüksek B değerlerinde ve
+
aynı y + mesafelerinde T ’da ortaya çıkan düşme
Şekil 3. Yüzeyden yapılan üfleme-emme uygulamasının
farklı B değerlerinde boyutsuz sıcaklık üzerindeki
etkisi
Üfleme-emme uygulamasının farklı B değerlerinde
boyutsuz sıcaklık üzerindeki etkisi Şekil 3’te görülmektedir.
5. Uluslararası İleri Teknolojiler Sempozyumu (IATS’09), 13-15 Mayıs 2009, Karabük, Türkiye
(a)
(b)
Şekil 4. Üfleme-emmenin (a) B = 0,03 ve (b) B=0,1 değerlerinde boyutsuz sıcaklık profili üzerindeki etkisi.
Düşük viskoz yutulma değerlerinde (şekilde 0,05≤B≤0
aralığındaki değişimler) üfleme uygulamasının viskoz
yutulmanın etkisini azalttığı, emme uygulamasının ise akış
alanındaki viskoz yutulma etkisini desteklemektedir. Viskoz
yutulmanın yüksek değerlerinde (B≥0,1) ise üfleme ile
viskoz yutulma etkisi artarken emme ile azalmaktadır.
Düşük ve yüksek B değerlerinde üfleme-emmenin viskoz
yutulma ve sıcaklık üzerindeki detaylı etkisi Şekil 4’teki
grafiklerde görülmektedir. Düşük ve yüksek viskoz yutulma
durumlarında üfleme ve emmenin sıcaklık değişimi
üzerinde farklı etkiler ortaya çıkarması, üfleme ve
emmenin hidrodinamik ve ısıl sınır tabakalar üzerindeki
farklı etkilerinden kaynaklanmaktadır. Zira düşük değerli
viskoz yutulma; yüzey yakınında düşük hız gradyanı
(düşük sürtme hızı) anlamına gelmektedir. Bu durumda
yüzeyden yapılan üfleme hız gradyanını daha da
düşüreceğinden yüzey yakınındaki viskoz yutulma etkisi
azalacak ve dolayısıyla viskoz yutulma kaynaklı ısı üretimi
de azalacağından akışkandan yüzeye olan ısı akısı
azalacaktır. Bu durumda doğal olarak yüzey yakınında
boyutsuz akışkan sıcaklığı az da olsa bir artış
gösterecektir. Benzer şekilde yüzeyden emme uygulaması
bunun tersi bir etki yaparak (hız gradyanının büyümesi ve
yüzeye ısı akısının artması) boyutsuz sıcaklıkta az da olsa
bir azalmaya neden olacaktır (Şekil 4.a). Ancak yüksek
değerli viskoz yutulma durumlarında yüzey yakınlarında
yukarıdakine benzer davranış gözlenmesine rağmen,
yüzeyden uzaklaşıldıkça üflemenin viskoz yutulma etkisini
artırmakta olduğu ve dolayısıyla boyutsuz sıcaklıkta
düşüşe neden olduğu görülmektedir. Burada ise yüzeyden
yapılan üflemenin hız gradyanı üzerinde fazla etkili
olmadığı ve yüksek viskoz yutulma nedeniyle üretilen
ısının arttığı ve dolayısıyla yüzeye ısı akısının da artması
nedeniyle boyutsuz sıcaklığın düştüğü anlaşılmaktadır.
Viskoz yutulma etkisi ile ortaya çıkan ısının sınır tabaka
içerisindeki sıcaklık dağılımını önemli ölçüde etkilediği
görülmüştür. Viskoz yutulma akışkandan yüzeye olan ısı
geçişini etkilemekte ve yüzey sabit sıcaklıkta tutuluyor olsa
bile artan viskoz etkiler nedeniyle ortaya çıkan ısı
yüzeydeki
akışkanın
sıcaklığında
bir
sıçramanın
oluşmasına ve üretilen ısının hem yüzeye doğru hem de
akışkana doğru geçmesine neden olmaktadır.
4. Sonuçlar
[1] Schlichting, H. and Gersten, K., Boundary-Layer
Theory, Springer, Berlin, 2000.
[2] Sumitani, Y. Kasagi, N., Direct numerical simulation of
turbulent transport with uniform wal injection and
suction. AIAA Journal 33, 1220-1228, 1995.
[3] Bellettre, J., Bataille, F. and Lallemand A., A new
approach for the study of turbulent boundary layers
Bu çalışmada; geçirgen yüzeyli ve sabit yüzey sıcaklığına
sahip düzlem levha üzerindeki gelişmiş sınır tabaka
akışında hidrodinamik ve ısıl duvar fonksiyonları elde
edilmiş, boyutsuz sıcaklık üzerinde üfleme-emme hızı ve
viskoz yutulmanın etkisi analitik olarak incelenmiştir.
© IATS’09, Karabük Üniversitesi, Karabük, Türkiye
Elde edilen sonuçlar göstermektedir ki; yüzey yakınlarında
ortaya çıkan yüksek gradyanlı akışlarda etkili olan viskoz
yutulma, yüzeyden yapılan üfeme-emme uygulaması ile
belirli ölçüde denetim altına alınabilir.
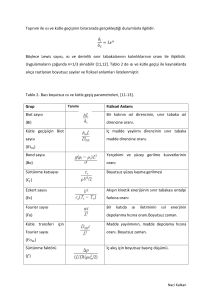
Semboller
uτ
ρ
qw
υ
T
Vw
u,v
cp
Kayma hızı (m/s)
3
Yoğunluk (kg/m )
2
Isı akısı (W/m )
2
Kinematik viskozite (m /s)
Sıcaklık (K)
Üfleme-emme hızı (m/s)
Hız bileşenleri (m/s)
Özgül ısı ( kj/(kgK )
Üst indisler
+
Boyutsuz parametreler
Alt indisler
w
Yüzeyde tanımlı büyüklükler
∞
Serbest akış büyüklükleri
Kaynaklar
Turan. O.. ve Çuhadaroğlu. B.
with blowing, Int. J. Heat and Mass Transfer, 42, 29052920, 1999.
[4] Hwang, C.B. and Lin, C.A., Low-Reynolds number k~ε modeling of flows with transpiration, Int. J. for
Numerical Methods in Fluids, 32, 495-514, 2000.
[5] Meinert, J., Huhn, J., Serbest, E. and Haidn, O.J.,
Turbulent boundary layers with foreign gas
transpiration, J. Spacecraft and Rockets, 38, 191-198,
2001.
[6] Çuhadaroğlu, B., Numerical study of turbulent
boundary layers with heat transfer and tangential
transpiration, Int. J. Numerical Methods for Heat and
Fluid Flow, vol. 14, no. 6, 760-782, 2003.