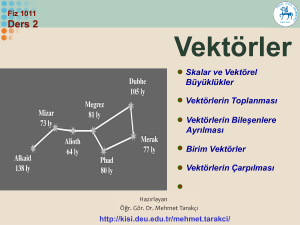
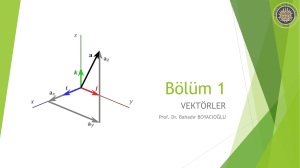
VEKTÖRLER:
İki çeşit fiziksel büyüklük vardır.
1. Skaler Büyüklükler: Bir rakam ve bir birim ile gösterilen büyüklüktür. Doğrultusu
ve yönü bulunmayan değerlerdir. Fizikte karşılaştığımız kütle, hacim, öz kütle,
zaman, iş, güç, enerji skaler büyüklükte değerlerdir.
2. Vektörel Büyüklükler: Ölçülebilen bir büyüklüğün yanında doğrultusu ve yönü de
bulunan büyüklüklerdir. Yer değiştirme, hız, ivme, kuvvet, elektrik alanı, manyetik
alan birer vektörel büyüklüktür.
Hareket eden bir araç için; harekete başladığı yerin, hareket doğrultusunun, aracın
nereye gittiğinin ve hızının büyüklüğünün belirtilmesi gerekir. Buna göre bir
büyüklüğün vektör olabilmesi için;
1. Yönü
2. Doğrultusu
3. Şiddeti
4. Başlangıç noktası
bilinmesi gerekir. Bir büyüklüğün vektör olduğunu gösterebilmek için üzerine ok
işareti konulur.
1. Yönü = + X yönünde
2. Doğrultusu = X doğrultusu
3. Şiddeti = A-B nin büyüklüğü
4. Başlangıç noktası = A noktası
VEKTÖRLERİN ÖZELLİKLERİ :
Bir vektörün yönünü, doğrultusunu ve şiddetini değiştirmeden ve ilk durumuna
paralel olmak şartıyla istenilen bir noktaya taşıyabiliriz.
180 derece yönü değiştiren bir vektörün işareti de değişir ya da işareti değişen
bir vektörün yönü değişmiş demektir.
Vektörel bir büyüklüğün bir sayı ile çarpımı ya da bölümü yine bir vektördür.
Yönü doğrultusu ve şiddeti ayni olan vektörler eşit vektörlerdir. Bu üç özellikten
birisi farklı olursa bu vektörler kesinlikle farklı vektörlerdir1.
K ile L aynıdır fakat M nin yönü zıt olduğundan K ve L kesinlikle farklıdır.(K = L = -M)
Skaler büyüklerde matematik işlemleri kullanırken vektörler büyüklerde farklı bir
matematik işlemi kullanır.
1
VEKTÖRLERİN TOPLANMASI :
İki yada daha fazla vektörün yaptığı etkiyi tek başına yapabilen vektöre bileşke vektör
denir.R ile gösterilir.
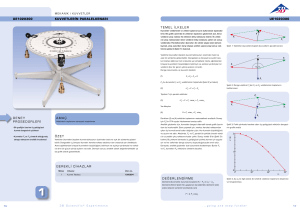
Paralel Kenar
Şekildeki A ve B vektörlerinin toplamı olan A+B vektörü paralelkenar metodu ile
çizilmiştir. A ve B vektörlerinden karşılıklı paralel çizgiler çizilerek, bir paralelkenar
oluşmuştur. Çizilen köşegen vektörlerin bileşkesidir.
Uç Uca Ekleme
Şekildeki A ve B vektörlerinin toplamı olan A+B vektörü uç uca ekleme metodu ile
çizilmiştir. A ve B vektörlerinden biri paralel olarak diğerinin ucuna taşınır ve ilk
vektörün başlangıcından son vektörün ucuna çizilen vektör bileşke vektördür.
Çıkarma
Vektörlerle yapılan çıkarma işlemi toplama işlemine benzetilerek yapılabilir. Şekil – I
de verilen aynı düzlemdeki K ve L vektörlerinden K – L vektörünü yani iki vektörün
farkını bulmak için, K + (– L) bağıntısına göre,
L vektörünü ters çevirip Şekil – II deki gibi toplamak gerekir. Eğer L – K vektörü
sorulursa, L vektörü aynen alınır, K vektörü ters çevirilip toplanır.
VEKTÖRLERIN DIK BILESENLERINE AYRILMASI
Her vektör birbirine dik iki bilesene ayrılabilir. Yani A vektörü öyle iki vektöre ayrılır ki
bu vektörler birbirine dik ve bileşkeleri yine A vektörüdür. Yandaki animasyonda F
vektörünün x ve y bileşenleri, F nin x ve y eksenlerindeki izdüşümleri çizilerek
bulunuyor.
Fizikte en çok kullanılan üçgenlerden birisi de 37, 90, 53 üçgenidir.
37° lik açının karşısındaki kenar uzunluğu 3 birim ise, 53° lik açının karşısındaki
kenar uzunluğu 4 birimdir. Bu durumda hipotenüs uzunluğu ise 5 birimdir.
Biz buna aynı zamanda 3, 4, 5 üçgeni diyoruz. Bu değerler, 3, 4, 5 in üst katları ve alt
katları olabilir.
Bir vektörün skaler le çarpımı ve skaler e bölümü
Bir vektörün skaler bir sayı ile çarpımı yine bir vektördür. Bu vektörün, yönü ve
doğrultusu değişmez, fakat şiddeti skaler sayı katı kadar değişmiş olur.
Bir vektörün bir skaler e bölümü yine bir vektördür. Çarpmada olduğu gibi oluşan yeni
vektörün yönü ve doğrultusu değişmez yalnızca şiddeti değişir.