bo ra 0 0 @ gma il.co m

ozeldersci.com
- K.K.A. 1 –
Büyük kenarın karşısındaki açı biliniyor ise;
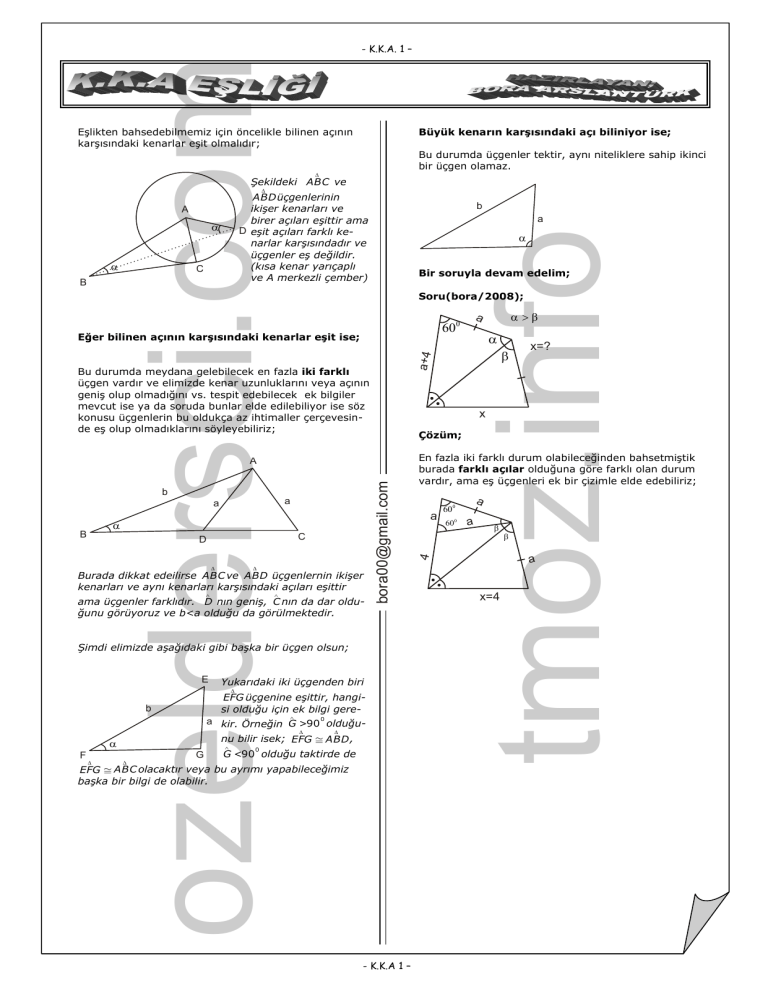
Eşlikten bahsedebilmemiz için öncelikle bilinen açının
karşısındaki kenarlar eşit olmalıdır;
Bu durumda üçgenler tektir, aynı niteliklere sahip ikinci
bir üçgen olamaz.
Δ
Şekildeki ABC ve
Δ
ABD üçgenlerinin
ikişer kenarları ve
birer açıları eşittir ama
D eşit açıları farklı kenarlar karşısındadır ve
üçgenler eş değildir.
(kısa kenar yarıçaplı
ve A merkezli çember)
α
α
B
C
b
a
α
Bir soruyla devam edelim;
Soru(bora/2008);
a +4
Bu durumda meydana gelebilecek en fazla iki farklı
üçgen vardır ve elimizde kenar uzunluklarını veya açının
geniş olup olmadığını vs. tespit edebilecek ek bilgiler
mevcut ise ya da soruda bunlar elde edilebiliyor ise söz
konusu üçgenlerin bu oldukça az ihtimaller çerçevesinde eş olup olmadıklarını söyleyebiliriz;
C
D
Δ
Δ
Burada dikkat edeilirse ABC ve ABD üçgenlernin ikişer
kenarları ve aynı kenarları karşısındaki açıları eşittir
^
^
ama üçgenler farklıdır. D nın geniş, C nın da dar olduğunu görüyoruz ve b<a olduğu da görülmektedir.
Şimdi elimizde aşağıdaki gibi başka bir üçgen olsun;
E
Yukarıdaki iki üçgenden biri
Δ
EFG üçgenine eşittir, hangisi olduğu için ek bilgi gere-
b
0
^
a kir. Örneğin G
>90 olduğuΔ
Δ
nu bilir isek; EFG t ABD ,
α
F
Δ
Δ
G
^
x=?
0
G <90 olduğu taktirde de
EFG t ABC olacaktır veya bu ayrımı yapabileceğimiz
başka bir bilgi de olabilir.
- K.K.A 1 –
En fazla iki farklı durum olabileceğinden bahsetmiştik
burada farklı açılar olduğuna göre farklı olan durum
vardır, ama eş üçgenleri ek bir çizimle elde edebiliriz;
a
4
α
B
β
Çözüm;
bora00@gmail.com
a
α
x
A
b
α >β
a
600
Eğer bilinen açının karşısındaki kenarlar eşit ise;
a
tmoz.info
A
a
600
600
a
β
β
a
x=4