İNÖNÜ ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
ELEKTRİK-ELEKTRONİK MÜH. BÖL.
325 ELEKTRİK MAKİNALARI LABORATUVARI I
TEK-FAZLI TRANSFORMATÖRÜN HİSTEREZİS DÖNGÜSÜ
DENEY 325-01
1. AMAÇ:
Tek fazlı transformatörün nüvesinin (demir çekirdeğinin) histerezis döngüsünü osiloskopta elde
etmek ve nüve kayıpları ile histerezis döngüsünün alanının ilişkisini belirlemek.
2. TEORİ:
2.1. Histerezis Döngüsü ve Nüve Kayıpları:
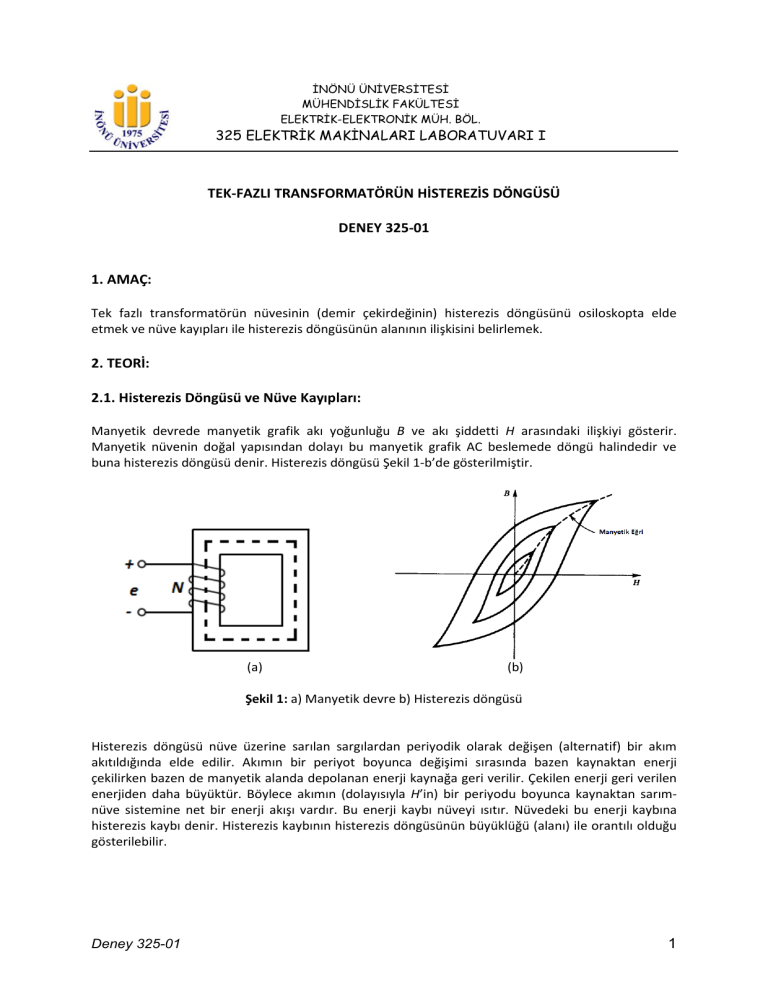
Manyetik devrede manyetik grafik akı yoğunluğu B ve akı şiddetti H arasındaki ilişkiyi gösterir.
Manyetik nüvenin doğal yapısından dolayı bu manyetik grafik AC beslemede döngü halindedir ve
buna histerezis döngüsü denir. Histerezis döngüsü Şekil 1-b’de gösterilmiştir.
(a)
(b)
Şekil 1: a) Manyetik devre b) Histerezis döngüsü
Histerezis döngüsü nüve üzerine sarılan sargılardan periyodik olarak değişen (alternatif) bir akım
akıtıldığında elde edilir. Akımın bir periyot boyunca değişimi sırasında bazen kaynaktan enerji
çekilirken bazen de manyetik alanda depolanan enerji kaynağa geri verilir. Çekilen enerji geri verilen
enerjiden daha büyüktür. Böylece akımın (dolayısıyla H’in) bir periyodu boyunca kaynaktan sarımnüve sistemine net bir enerji akışı vardır. Bu enerji kaybı nüveyi ısıtır. Nüvedeki bu enerji kaybına
histerezis kaybı denir. Histerezis kaybının histerezis döngüsünün büyüklüğü (alanı) ile orantılı olduğu
gösterilebilir.
Deney 325-01
1
Şekil 1’deki sarımların dirençlerinin sıfır ve nüvedeki akının olduğunu varsayalım. Sarımlarda
indüklenen gerilim
d
(1)
eN
dt
olur. t1 ’den t2 zamanına kadar transfer olan enerji
t2
W e i dt
(2)
t1
Denklem (1) kullanılırsa
W N
d
i dt
dt
2
N i d
(3)
1
elde edilir. B A ve i
H lc
olduğundan
N
B2
W N
B1
H lc
AdB
N
B2
lc A H dB
(4)
B1
B2
Vnüve H dB
B1
bulunur. Burada Vnüve nüvenin hacmidir. İntegral terimi Şekil 3’deki alanı gösterir. Böylece bir periyot
boyunca transfer edilen enerji
W Vnüve H dB
(5)
VnüveWh
eşittir. Burada Wh nüvedeki enerji yoğunluğudur ve histerezis (B-H) döngüsünün alanına eşittir.
Böylece histerezis etkisinden dolayı oluşan güç kaybı
Ph Vnüve Wh f
(6)
olur. Burada f akımın değişim frekansıdır.
Şekil 3: Histerezis kaybı
Zamanla değişen bir akı nüve üzerine sarılan bir sargıdaki gibi nüve üzerinde girdap şeklinde akımların
akmasına neden olur. Nüvenin direncinden dolayı nüve üzerinde kayıp oluşur ve nüve ısınır. Bu
kayıplara girdap (fuku) akım kayıpları denir. Akımın frekansı artıkça girdap akım kayıpları da artar.
Deney 325-01
2
Histerezis ve girdap akım kayıpları birleştirilerek nüve kayıpları olarak adlandırılır. Eğer sargılardan
geçen akımın değişimi yavaş (düşük frekanslı) ise girdap akım kayıpları ihmal edilecek kadar küçüktür.
Yavaş değişen akıma (manyetik akı şiddettine) göre elde edilen B-H eğrisine statik döngü (histerezis
döngü) denir. Eğer sargılardan geçen akımın değişimi hızlı ise B-H eğrisi daha belirgin hale gelir ve
dinamik döngü (histero-girdap akım döngüsü) olarak adlandırılır.
Şekil 3: Statik ve dinamik döngü
2.2. Histerezis Döngüsü ve Nüve Kayıplarının Elde Edilmesi:
Uygun sinyaller kullanılarak histerezis döngüsü osiloskopta gözlenebilir. Histerezis döngüsü manyetik
akı yoğunluğu B ve manyetik akı şiddetti H’ın çiziminden elde edildiğinden, bu değerlerle direk
orantılı ve aynı fazda olan sinyaller kullanılmalıdır.
Transformatör sarımlarında indüklenen gerilim
d
eN
dt
(7)
ve B A olduğundan
d (BA)
dB
NA
dt
dt
1
1
dB
edt
v p dt
NA
NA
eN
1
dB N A v
p
dt
(8)
(9)
1
v p dt
NA
elde edilir. Böylece akı yoğunluğu sinyali sargılara uygulanan gerilimin integrali alınarak elde
edilebilir. Bunun için seri bağlanan bir RC integratörü kullanılabilir. Şekil 4’deki devrede eğer
1
ise
R1
C
v
ic p
(10)
R1
olur. Böylece kondansatör gerilimi
B
Deney 325-01
3
1
ic dt
C
1 v
vc p dt
C R1
1
vc
v pdt
CR1
olur. Akı yoğunluğu sinyali kondansatör gerilimi ile doğrudan orantılıdır.
vc
(11)
Transformatör için
H lc N i
(12)
N
i
lc
eşittir. Böylece manyetik akı şiddeti sinyali sargılardan geçen akım ile doğrudan orantılıdır.
Sargılardan geçen akım sargılara seri bağlanan küçük bir direnç üzerinde düşen gerilim kullanılarak
ölçülebilir. Şekil 4 histerezis döngüsünün elde edilebileceği bir devre bağlantısını göstermektedir.
H
3. ÖN ÇALIŞMA
a) Deneyin amacını kısaca açıklayınız.
b) Eğer kaynak gerilimi sinüs ve rms değeri 220V ise devre parametrelerini kullanarak Şekil
4’deki kondansatör üzerinde görülecek gerilimin şeklini çiziniz ve tepe değerini hesaplayınız?
c) Osiloskobun izolasyon trafosundan beslenmesi neden önemlidir?
3. DENEYİN YAPILIŞI
Şekil 4’deki devreyi kurunuz.
Transformatör
220:48V
Varyak
A
R1= 1MΩ
220V
Wattmetre
Y(CH2)
Vp
Vs
4.2µF
2Ω
X(CH1)
Şekil 4: Histerezis döngüsünün elde edilmesi için bağlantı devresi
Dikkat!
Deney başlamadan osiloskobunuzun izolasyon
trafosundan beslendiğine dikkat ediniz.
a) Varyak vasıtasıyla primer gerilimini maksimuma ayarlayınız. Osiloskopun X girişinden elde
ettiğiniz akım şeklini maksimum gerilim, 200, 150, 100, 50 ve 20 V için gözlemleyiniz ve her
bir değer için çiziniz.
Deney 325-01
4
b) Varyak vasıtasıyla primer gerilimini maksimuma ayarlayınız. X ve Y girişlerini ayarlayarak
maksimum gerilim için en büyük histerezis döngüsünü elde ediniz. X ve Y’nin ayarlarını
değiştirmeden maksimum gerilim, 200, 150, 100, 50 ve 20 V için histerezis döngüsünü
gözlemleyiniz ve her bir değer için çiziniz. Her bir değer için histerezis döngüsünün yaklaşık
alanını, güçü ve akımı not ediniz.
4. SONUÇLAR
a) Nüve kayıplarını gerilim değerlerine karşılık çiziniz.
b) Nüve kayıplarını gerilimin karesine karşılık çiziniz.
c) Histerezis döngüsünden yaklaşık olarak elde ettiğiniz alanı gerilim değerlerine karşılık çiziniz.
5. SORULAR
a) Deney 3.a’da elde ettiğiniz akım şekillerini harmonik içeriğini dikkate alarak yorumlayınız.
Gerilim yükseldikçe akım şeklinin bozulduğunu gözlemlediniz mi? Nedenini belirtiniz.
b) Nüve kayıpları-gerilim grafiği ve histerezis alanı-gerilim grafiği bir birine benzemekte midir?
Açıklayınız.
Deney 325-01
5












