Kontrol Sist. Lab. Föyü(BK-İBK-BH-İBH-A1-A2-A3
advertisement

1232
56756769
7
569
7
6675959
75959
56
77
67667
9
2!!2"#"$"%#&"'2(")*
(v.1203180104.otokontrol.foy)
+,-.-/010276
6.3-4.-5202666
78&9:';<:&<:&:289=2#&
$8%:%2>::>;<:&<:&:289=2#&
7##?@AA?">#:2<:&<:&:289=2#&AB78&9:'
7##?@AA?">#:2<:&<:&:289=2#&AB$8%:%2>::>
C"#@D=E0F+.0GH0.I4JK257##?@AA?">#:2<:&<:&:289=2#&AB$8%:%2>::>AL8M
F0NE02GO1O2P025.Q35FQEQ.R7##?@AALLL2S"%#&"'L"&'92#$AF0NE02GO1OQE5T5FG0F02EOU5
1QVKE01J+2HJWHE0V01O+E026X1Q1G5VQ53EQNQ2P51+.HE0.O2OY0,4YKVFHE0FQEQ.1Q2QY-
6
RZ[\[
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
565789:5;9<=
>?>@A%>BACDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD1/
8!EF!8! DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDG/
.>+BAH)ABIJ%)ABKA?LMN"HNOKAHABA@AIBAC>DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD3/
FEF0PQDQDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD3/
RSTSU/VWTXYX/Z/W[\][^_T/\`abc`defghcRiefijaka/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/m/
RSTSU/\]\n_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/m/
RSTSU/SoS]\To\p_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/m/
RSTSU/i`abqihiras/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/m/
RSTSU/rghtqiruvjws/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/m/
RSTSU/\R_]o\p_Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/m/
YWpXo\p/xRSTSUyzlz{Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/|/
FEF0PQD1DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDQQ/
RSTSU/VWTXYX/Z/SegfdjcUtbrdq}d`/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zz/
RSTSU/\]\n_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zz/
RSTSU/SoS]\To\p_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zz/
RSTSU/i`abqihiras/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zz/
RSTSU/rghtqiruvjws/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zz/
RSTSU/\R_]o\p_Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zz/
YWpXo\p/xRSTSUyzl~{Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z~/
FEF0PQD4DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDQ/
RSTSU/VWTXYX/Z/SegfhdudjcUtbrdq}d`/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
RSTSU/\]\n_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
RSTSU/SoS]\To\p_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
RSTSU/i`abqihiras/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
RSTSU/rghtqiruvjws/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
RSTSU/\R_]o\p_Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
YWpXo\p/xRSTSUyzl{Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z/
FEF0PQDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDQ3/
RSTSU/VWTXYX/Z/W[o\]\/Rdefdrg/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zm/
RSTSU/\]\n_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zm/
RSTSU/SoS]\To\p_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zm/
RSTSU/i`abqihiras/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zm/
RSTSU/rghtqiruvjws/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zm/
RSTSU/\R_]o\p_Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/zm/
YWpXo\p/xRSTSUyzl{Z/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/z|/
FEF0PQDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD1
/
RSTSU/VWTXYX/Z/`_V\p]\/Rdefdrg/llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/~/
RSTSU/\]\n_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/~/
RSTSU/SoS]\To\p_Z/lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll/~/
012340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
45657/89:;<8=8>:?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/AB/
45657/>C=D<8>EFGH?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/AB/
45657/I4JKLIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/AB/
OPMQLIM/R45657ST@UVN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/AT/
WXW0YZ[\[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[]^/
45657/_P6QOQ/N/`abC<C=cCd<aECeC/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Af/
45657/IKIgJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Af/
45657/5L5KI6LIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Af/
45657/89:;<8=8OJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Af/
45657/>C=D<8>EFGH?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Af/
45657/I4JKLIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Af/
OPMQLIM/R45657ST@hVN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/AU/
WXW0YZ[3[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[]3/
45657/_P6QOQ/N/iDbajcILJgJ/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Ak/
45657/IKIgJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Ak/
45657/5L5KI6LIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Ak/
45657/89:;<8=8OJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Ak/
45657/>C=D<8>EFGH?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Ak/
45657/I4JKLIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Ak/
OPMQLIM/R45657ST@kVN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/Al/
WXW0YZ[m[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[1n/
45657/_P6QOQ/N/C6i5`MIL/ILJgJ/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oB/
45657/IKIgJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oB/
45657/5L5KI6LIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oB/
45657/89:;<8=8>:?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oB/
45657/>C=D<8>EP6QN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oB/
45657/I4JKLIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oB/
OPMQLIM/R45657ST@pVN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oA/
WXW0YZ[q[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[11/
45657/_P6QOQ/N/`abC<C=SI_JK/4rGDstDbDeDcR7DdaGcED;<a=au/C;Ccv8t<:cw8x<8Gt:V/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oo/
45657/IKIgJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oo/
45657/5L5KI6LIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oo/
45657/89:;<8=8>:?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oo/
45657/>C=D<8>EP6QN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oo/
45657/I4JKLIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oo/
OPMQLIM/R45657ST@lVN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/oU/
WXW0YZ[Zn[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[[13/
45657/_P6QOQ/N/`abC<C=SI_JK/4rGDstDbDeDcRiFyb8;<8G=:scED;<a=au/ia;cv8t<:cw8x<8Gt:V/@@@@@@@@@@@@@@@@@@@@/ok/
45657/IKIgJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/ok/
45657/5L5KI6LIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/ok/
45657/89:;<8=8>:?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/ok/
45657/>C=D<8>EFGH?/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/ok/
45657/I4JKLIMJN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/ok/
OPMQLIM/R45657ST@TBVN/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@/ol/
012310
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
,$56787*5)9:5%;7:5<7=85*">?@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@1A/
BCB0DE@A@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@1A/
FGHGI/JKHLML/N/KOPHQR/GSGTPHR/QUVUWXYZU[MU\]Y^UW[_G`PaR/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cd/
FGHGI/PTP_RN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cd/
FGHGI/GSGTPHSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cd/
FGHGI/efgZhe^e\gi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cd/
FGHGI/\U^jhe\kKHLN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cd/
FGHGI/PFRTSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cd/
MKOLSPO/lFGHGImnbdoN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cn/
BCB0DE@E@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@1p/
FGHGI/JKHLML/N/qPTPH/MerU]U[ldb/FGOG_Go/GSGTPHR/QUVUWXYZU[MU\]Y^UW[_G`PaR/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cs/
FGHGI/PTP_RN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cs/
FGHGI/GSGTPHSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cs/
FGHGI/efgZhe^e\gi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cs/
FGHGI/\U^jhe\kKHLN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cs/
FGHGI/PFRTSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cs/
MKOLSPO/lFGHGImnbnoN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/ct/
BCB0DE@4@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@1u/
FGHGI/JKHLML/N/QU]vYwU^[GSGTPHR/lnbFGOG_Go/QUVUWXYZU[MU\]Y^UW[_G`PaR/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cx/
FGHGI/PTP_RN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cx/
FGHGI/GSGTPHSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cx/
FGHGI/efgZhe^e\gi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cx/
FGHGI/\U^jhe\kyWzi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cx/
FGHGI/PFRTSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/cx/
MKOLSPO/lFGHGImnb{oN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/s|/
}"~";$%~:;:;@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@pE/
BCB0D4@A@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@pE/
FGHGI/JKHLML/N/KHK/lPfJPPo/JyW]vyh
v/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sn/
FGHGI/PTP_RN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sn/
FGHGI/GSGTPHSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sn/
FGHGI/efgZhe^e\gi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sn/
FGHGI/\U^jhe\kyWzi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sn/
FGHGI/PFRTSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sn/
MKOLSPO/lFGHGIm{bdoN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/sc/
BCB0D4@E@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@p/
FGHGI/JKHLML/N/R/JyW]vyh
v/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/st/
FGHGI/PTP_RN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/st/
FGHGI/GSGTPHSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/st/
FGHGI/efgZhe^e\gi/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/st/
FGHGI/\U^jhe\kKHLN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/st/
FGHGI/PFRTSPORN/bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb/st/
012340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:7/;<=>=?@ABCDE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/FG/
HIH0J4K4KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKLM/
<=>=?/N6>858/E/OP</NQRSTQUVT/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WX/
<=>=?/:Y:ZPE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WX/
<=>=?/=9=Y:>9:7PE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WX/
<=>=?/[\]^U[_[`]a/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WX/
<=>=?/`b_cU[`dQRea/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WX/
<=>=?/:<PY9:7PE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WX/
56789:7/;<=>=?@ABADE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WA/
fK80Hgh80Hi0HjkljmnKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKL1/
HIH0JfKoKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKL1/
<=>=?/N6>858/E/pBqB/<Z/5=7r6/5b̀Ss_tustOP</NQRSTQUVTtbUst<sRsSUsR_s`b/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WF/
<=>=?/:Y:ZPE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WF/
<=>=?/=9=Y:>9:7PE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WF/
<=>=?/[\]^U[_[`]a/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WF/
<=>=?/`b_cU[`d6>8E/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WF/
<=>=?/:<PY9:7PE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WF/
56789:7/;<=>=?@pBqDE/BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB/WG/
m"vwmxmyj%%"v"%)"Iz!{|KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKL}/
w~w"~n%%wy~mwll"wm"~"mjm)nl"wm"ig! HI!0 gKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKK3o/
w~w"~n%%wy~mwll"wm"~"mjyjk"l+~|h!{0 g! |KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKK3/
l"wm"~"mm"vwm
)*j~~j%"~KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKK3/
012340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56786596:;
/
<=>?@ABC?DBDEFG@H/IF@JBCKLMKNOBPQQROBSGGTUVVWWWXYZLGJZNWZJN[XG\]^_`abcbde^fg^`hiji^
PQQRkBB
l=>minoh^poioq^rsbiio^rtsocq^uvohwxoi^yz{sazi^vbxs|di|ab^}^~|{|h^hi|ab{b{^
owaio{doxwu^bxo{xBbsbad|^
|bq^oadoao^{b|axbs|xb^
|t{bt^`bsbd^otjis|xbq^
xso{iq^ffB
=>vohwxoi^yz{sazi^g^~|ax^zsioawq^paz^~a^ao{|ssb{^o{q^xso{iq^ff^B
=>GZHKG\BZLGJZNB^~|ax^zsioawq^a^~z^~a^oxo{^`aoiq^xso{iq^ff^B
=>C ¡¢ £B¤X¥XQB¦@NTBVB§ZLGJZNBDEFG@HB¡ZZNAZ¨B
©=>ªa^rabziq^|doi|ssb{^yosq«r
r^|^j|{bxibt^ªh¬iodoioaw«^rr^
PQQ­BB
®=>rabo{^ba|{q^ox|^a|{b|a^q^¯r
r^za^`{¬b{||ax«^q^pa|{sbn|^oiiB
°=>y^m¬oso^¯~bxna|s|sbd|^z{sazi^vhxs|dx«q^pa|{sbn|¦KNNB±LG@JLKGZLKNB²RR¥kXBB
³=>£EBGS@B́@µ@LGFBZ¶BGS@BIL·@JFGEBZ¶BCYSµKLXB̧V¸VR¤B§¹§B
²SGGTUVVWWWX@LµLXMHYSX@[MVµJZMTVYGHkB
<º=>»zio{^v^a{x^q^¯ro{n|^z{sazi^`{¬b{||ab{¬«^q^ss|a¼zs¦@L@HKLLBPQQB
<<=>v|it^{b|axbs|xb^
|t{bt^bibdi|a^|xi|t^jtx|tzti^
|t{btLNL@B½@JµB§NGB¾OB
vohwe¿PQQ¤B
<l=>rhz^À^mÁsbdoi¡MLLµBZ¶B±½B§ZLGJZNN@JBÃKLFBIFLµBÃ@L@GYB
<=>ri¬zabsdxq^podttoi|^{b|axbs|xb^j|{bxibt^otjis|xb^j|{bxibt^bibdi|ab^
½@JµFOBPQQÄOVO­­ÄB
<=>Åziot^q^ohw{wa^»q^p}^gÆ^bi|^~r^zsza^w^yz{sazijq^podttoi|^
{b|axbs|xbBj|{bxibt^otjis|xb^j|{bxibt^bibdi|ab^~|a¬bxbq^ffÇq^ggPOBP¤¤
P¸ÄB
<=>ownw^^y|{b{|{^rhoaiodoiw^vohwxoi^p}~^
oxoawdwq^jtx|t^bxo{x^
|bB
<©=>È»|b¬q^¯rÁÁib|^~b¬bsoi^z{sazi^
|zah^q^~|xb¬{^o{^}dÁi|d|{sosbz{«^B
<®=>ÉYSZNKFBDS@AN@OB±L¡@YSOBÊ?SKGBFB±½BYZLGJZNBKLEWKEËÊOB±D BB¡S@B±LFGJMH@LGKGZLOB
vhxs|dxq^o{^rszdosbz{^vznb|shq^Èo{^gÌÌÌ^_Å|babe^`aso{^rt¬jiq^
ÍJGKLX \µMNÎH@GJZNZÏztinzdsaq^xo{^rthjq^}xo{rthÐd|sazizÑb
Z\MNMXYZHXGJkB
;
012340
TEORĐK BĐLGĐ
Sayfa 1 / 8
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.1):
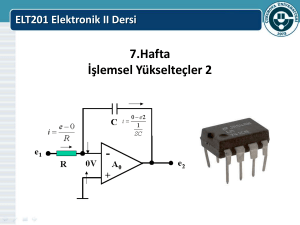
Aşağıda bir OPAMP entegresi ile gerçekleştirilmiş açık çevrim davranışı gözlemlemek üzere
kullanılan bir devre şeması görülmektedir.
Opampların çok yüksek gerilim kazançlarından dolayı geri besleme olmaksızın kontrol edilebilmeleri
çok güçtür. Bu tür çalışmadaki gerilim kazancına "açık çevrim gerilim kazancı" denir. Burada bu
kazanç değeri "K" ile sembolize edilmiştir.
OPAMP elemanları temel işlevi fark yükselteci (differential amplifier) olarak çalışmalarıdır.
Yukarıdaki devre için OPAMP elemanının girişleri V1 ve V2 ile çıkış ucu Vo, açık çevrim kazancı K
ve simetrik besleme uçları +V ve -V'dir. Fark yükselteci olarak OPAMP elemanı için giriş ve çıkış
uçları arasındaki ilişkiyi matematiksel olarak şu şekilde ifade edebiliriz:
Vo = K * ( V2 - V1 )
K kazanç değeri teoride sonsuz (∞) kabul edilir. Ancak, fiziksel anlamda elektronik elemanların sahip
oldukları sinırlılıklar nedeniyle uygulamada K değeri 10^6 ile 10^8 değerleri arasındadır. En kesin
değer için ilgili OPAMP entegresinin datasheet dokumanından OPAMP elemanının açık çevrim
kazanç değerine (K) bakılabilir. Örneğin 741 serisi OPAMP entegreleri için datasheet dökümanında K
değerinin 10^8 civarında olduğu belirtilmektedir.
OPAMP'ın temel işlevi olan fark yükselteci olarak çalışması düşünüldüğünde yukarıda verilen
formüle dikkat edilirse OPAMP pozitif (+) uçlu girişindeki işaretten negatif (-) uçlu giriş işaretini
çıkartmakta ve farkı da K kazanç değeri kadar yükselterek çıkışa vermektedir. Bu denklemden dikkat
edilirse giriş çıkış arasındaki çok küçük bir işaret farkı bile OPAMP'ın sahip olduğu K kazancından
dolayı çıkışta çok yüksek mertebelere ulaşacaktır.
Teoride OPAMP'ın K değerinin sonsuz (∞) olması nedeniyle Vo çıkış ucundaki sinyal için aşağıdaki
sonuçlara varılabilir:
Eğer V2 > V1 ise Vo = + ∞ (teoride)
Eğer V2 < V1 ise Vo = - ∞ (teoride)
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 8
Uygulamada ise bir OPAMP elemanının maksimum sınırlılığı elemanın besleme gerilimleri kadar
olacaktır. Bu duruma göre açık çevrim çaalışan OPAMP elemanı çıkışı ya +V (+Vcc) ya da -V (-Vcc)
simetrik besleme gerilimleri kadar olacaktır. Bu durumdan hareketle pratikte OPAMP'ın Vo çıkış
ucundaki sinyal için aşağıdaki sonuçlara varılabilir:
Eğer V2 > V1 ise Vo = + V (pratikte)
Eğer V2 < V1 ise Vo = - V (pratikte)
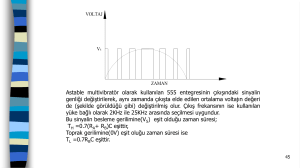
Đdeal bir op-ampın kazancı sonsuzdur. Gerçek bir op-ampın kazancı ise normalde 100.000 (100dB)
dır. üstte bulunan grafiğe baktığımız zaman giriş gerilimi mili voltlar civarında salınırken bunun
sonucunda elde edilen çıkış gerilimi +Vcc ve -Vcc (+12V ve –12V) arasında değişmektedir. Çoğu
durumda kazanç aşırı derecede fazladır. Bunu engellemek için negatif geri besleme direnci ilave
edilir. Yukarıdaki grafikte Sağ tarafa baktığımızda op-ampın kazancı sağa doğru azalmaktadır.
Kazanç, frekans arttıkça hızlı bir şekilde düşmektedir. Aslında band genişliği (çıkışın 3dB düştüğü)
1KHz’dir. Band genişliği negatif geri besleme direnci koymak suretiyle arttırılabilir.
Op-ampların giriş empedansı idealde sonsuzdur. Ancak gerçekte çok yüksektir. Örneğin 1MW. Çıkış
empedansı idealde 0’dır. Ancak gerçekte çok düşüktür. Örneğin 150W.
Opamp’ın geri beslemesiz (açık çevrim) çalışmasını incelemek için şekil-1' deki
deney devresini incelersek. Güç kaynakları açıldığında ve devre dikkatlice inceleyelim. Opamp
elemanının çıkış ucu boşta bırakılmış, çıkış ucu ile giriş ucu arasında geri besleme yapılmamıştır.
Opamp çıkışında elde edilen gerilim ölçüldüğünde giriş gerilimi şase (0V) potansiyelinde olduğu
halde çıkış geriliminin +V veya –V besleme gerilimine kilitlendiği görülecektir. Çünkü,
OPAMP elemanı sahip olduğu giriş ucu emepedanslarının tam simetrik olmamasına bağlı olarak aynı
işaretin her iki ucuna uygulanması pratikte OPAMP elemanının bu sinyali kendi içinde biri büyük
diğeri küçük şekilde değerlendirmesine neden olacak ve bu şekilde de çıkış işareti OPAMP'ın pozitif
ya da negatif besleme gerilimi ile doyumda olacaktır.
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 8
Çıkış işaretini voltmetrede tekrar gözlemlediğimiz zaman Opamp’ın geri beslemesiz (Açık çevrim)
çalışmasını incelemeye devam edelim. Opamp’ın her bir girişine uygulanan işaretlerdeki değişimler
opamp çıkışını nasıl etkilemektedir. Bu durumu incelemek amacı ile şekil-2’deki bağlantılardan
faydalanacağız. Devreyi dikkatlice incelersek opamp’a geri besleme yapılmamıştır. OPAMP ’ın
negatif (eviren) girişine 10KΩ’ luk pot üzerinden +12V ile –12V arasında ayarlanabilen bir gerilim
uygulanacaktır. Negatif girişe uygulanan bu gerilimin, OPAMP çıkışına yaptığı etkiye bakıldığında
OPAMP'ın negatif ucuna +12 V dan itibaren azalan pozitif işaretli sinyal uygulanırsa çıkış ilk anda -V
besleme geriliminde olacak, ancak negatif girişteki sinyal değeri negatif değerler almaya başladığı
anda bu sefer OPAMP çıkış noktasında pozitif değerler görülmeye başlanacaktır. Çünkü, negatif giriş
ucundaki negatif değerler (şase, yani sıfır (0)'dan küçük )değerler için temel fark işlevi gereği (negatif
girişteki işaret de fark işlevinden dolayı terslenecek) OPAMP çıkışında pozitif sinyal görülecektir.
Açık çevrim çalışmada eviren girişin opamp çıkışına etkisini yukarıda inceledik. Bu bölümde
evirmeyen (pozitif) girişin çıkışa etkisini inceleyeceğiz. Bu işlem için şekil-3’te görülen devre
kullanılacaktır. Devreyi dikkatlice incelerseniz eviren giriş şase potansiyeline bağlanmış, giriş işareti
evirmeyen girişten uygulanmıştır. Devreyi dikkatlice incelersek OPAMP ’a geri besleme
yapılmamıştır. Opamp’ın pozitif (evirmeyen) girişine 10KΩ’ luk pot üzerinden +12V ile –12V
arasında ayarlanabilen bir gerilim uygulanacaktır. Pozitif girişe uygulanan bu gerilimin, OPAMP
çıkışına yaptığı etkiye bakıldığında OPAMP'ın pozitif ucuna +12 V dan itibaren azalan pozitif işaretli
sinyal uygulanırsa çıkış ilk anda +V besleme geriliminde olacak, ancak pozitif girişteki sinyal değeri
negatif değerler almaya başladığı anda bu sefer OPAMP çıkış noktasında negatif değerler görülmeye
başlanacaktır. Çünkü, pozitif giriş ucundaki pozitif değerler (şase, yani sıfır (0)'dan büyük )değerler
için temel fark işlevi gereği OPAMP çıkışında pozitif sinyal görülecektir.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 8
A çık çevrim çalışmada; Opamp’ın eviren ve evirmeyen girişleri birlikte kullanılırsa OPAMP çıkışı
nasıl etkileneceğini incelemek için şekil-4’daki devreden yararlanılacaktır. Bu tür çalışmaya;
opamp’ın Gerilim karşılaştırıcı (Voltage comparator) olarak çalışması denir. Özellikle iki farklı
büyüklüğü ölçmek veya karşılaştırmak amacı ile endüstride sıkça kullanılır. Ancak, komparatör
olarak çalışma olarak değil, burada çıkış işareti OPAMP'ın girilerine göre ya +V ya da -V besleme
gerilimleri değerinde doyumda olacaktır. Bu devrede dikkat edilmesi gereken pozitif uçtaki sinyal
değeri negatif uçtaki değerden büyük ise çıkış pozitif doyum değerinde olacaktır. Örneğin V2>V1
çıkış pozitif doyum yani (+V değerinde) ve benzer şekilde V2<V1 ise çıkış negatif doyum, yani -V
besbelem gerilimde olacaktır. Bu örnek için +V ve -V OPAMP besleme gerilimleri sırasıyla +12 V ile
-12 V değerlerinde seçilmiştir.
Aşağıda yapılmış bir deneyin sonuçları verilmiştir. Lütfen inceleyiniz.
Buna göre V1>V2 durumu:
V1= +10V
V2= 2V(100Hz) verildi.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 8
V1>V2 durumunda sinüs dalga V2 gerilimi hiçbir zaman V1 geriliminin üstüne çıkmayacağı için
alacağımız cevap –V0 gerilimi olacaktır. Bu deneyde opampın –V besleme ucuna -15V verilmesine
rağmen ölçülen değer -12,2V tur. Bunun nedeni opamptan kaynaklanan hatalar veya ölçüm
hatalarıdır.
V1<V2 durumu:
V1= +0,5V
V2= 2V(100Hz)
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 8
Bu durumda 1. zamanda V2>V1 olduğu için çıkıştan +V besleme gerilimini elde ettik. 2. zamanda
V1>V2 olduğu için çıkıştaki cevap –V besleme gerilimi olur. Böylece çıkışta bir kare dalga oluşur.
V1<V2 durumu:
V1= -10V
V2= 2V(100Hz)
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 8
Opampa verilen giriş sinyallerinin V1<V2 olması ile opamp çıkışta +V besleme gerilimi olur.
2. adımda eviren ve evirmeyen uçlardaki kaynakların yerini değiştirdik. Buna göre
V1>V2 durumu:
V1= 10V
V2= 2V(100Hz)
Bu durumda opampın evirmeyen ucuna V1 gerilimi V2 gerilimimden her zaman büyük olduğu için
çıkışta alınan cevap +V besleme gerilimi olur.
V1<V2 durumu:
V1= 0,5V
V2= 2V(100Hz)
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 8
V1<V2 durumu:
V1= -10V
V2= 2V(100Hz)
Sonuç olarak opampın eviren ucuna gelen gerilim büyük olursa –V besleme gerilimi, evirmeyen
ucuna gelen gerilim büyük olursa +V besleme gerilimi çıkış olarak alınır.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_01/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
456789:;<:9=>?@<:9A:B=CDEF;EG=A:;:9=H:I:>9:J76
KLMLN6OPQRQ6STMQUQV6WXYZ[\ZY]^_`\ZYaZb]cdefgeh]aZ[ZY]iZjZ^YZkWl
KLMLN6MT6V6454566
KLMLN6STMQUQ6V6Tmnompqr=Fsqt=Buvwxy=Hzvwzrq{q6
KLMLN6non|}V66
4~ldefge]
]]]]
]
]]
]
]
]
]]l
~ldefge]
]]
]
]l
~l]]]
]]
]
]l
KLMLN6LLonMnP}V66
l ¡¢£l¤¥ldefge¦l
H:I:>=FB§@9F;F<§¨=6
©ª]]]]]]
]]]«]
]¬
]ªª
]
­]ª
]®\Z\]]«]
]ª
]¬¯]°££±²³³́´´¦µ¶·£̧¶¹́¶¸¹¡¦£º³l
´¢»l ¡¸¢¼½·½l¾½¿ ¸¢£l¢¡¢»½¹½¸¼½·½¾¦ll
KLMLN6<7;?9F<>DIÀV66
©ª]]]«]
]¬
]ªª
]­]ª
]®\Z\]]«]
]ª
]]°££±²³³́´´¦µ¶·£̧¶¹́¶¸¹¡¦£º³ĺ¢»l ¡¸¢¼½·½l¾½¿ ¸¢£l¢¡¢»½¹½¸¼½·½¾¦ll
KLMLN6nK}onP}V66
4~lX]]ªªª¯]cÁÂ[Â]ÃÄÅ]Æ]]ª]i®]
]¯h]ll
l
l
~lZ]]i®Ç]]]]]È
¬]Æ]]]
]l
Éʾ˹½ºlfÌl
]ªª
¯lÍMÎÏVlZlª]
]]]]]
]
Т¸Ñ½¿¶¸¼ l
]È
¬]]]
l]]]
]
·¢l¯]¯¬]¯]cÒ]ª]]ÄÆ]]]Ó]Æ]
]]]
]
]]^
]
]È
¬]]Ä]Æ]
012130
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567689:56:;<=;>6?<;@;ABCD;567689:56:;E<=C<;F98;G6:C9H;567689;H9;FI;56768;JKLMNOMPOQLRSLTM
9UD6:9C6:;@;ABCD;567689:6;<?<8C<:<VW?B8;BCUI:X;FI;5I8IV<;:<UWC;F98;YZ=[V;I?GIC<8UW:W=\]^MM
M
_`Ma?GIC<5W7W:W=;A@;>6;Ab;G689C9VC689:9:;G6:C979:9c;M
M
defdghMdeidgMjLkLlLNMdehMdghMdJMG689C9VC689:9:;5<CG<;m6HC9:9;<CD;<CD<;Y9=9:9=;>6;
UB:IYC<8W:W=W;?B8IVC<?W:W=n;M
o`MA@;>6;Abp:9:;?689:9;5679mD98686H;qn;<5WVW;D6H8<8C<?W:W=;>6;UB:IYC<8W:W=W;?B8IVC<?W:W=n;M
rstuMvHU9;F6C98D9CV659HY6;wxvyxpC<8Mz{A||;9Y9:]M{@};A;p;C<;F6UC6:6|6HD98n~~
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
~
s~
r`u~~
M
012340
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:;<=>?<@ABCDEFGFBHCHABIJJKLMMNNNOP;AJ<;>N;<>QOJRMBSNTUBU?V>?AJ@W@AQ?ABXY:Z:B
[\[]^_\`^Sa\]SbcSd^`^e\`SfgTAThBihj=>?G?W@fBUD>FGFAFBR=>>?A?<?RBh?<Q@GB?>?UH>H<kBQTAThB
I?RR@AQ?B?h<@AJ@>@BJT;<HRBUH>jHBHCHABQTBhHATB?hA@BWHWJTGHABU=BQTAThTB?HJBJT;<HRBUH>jHBUD>FGFAQTAB
ealalma`ab\m\l[\`\noSS
S
pqrs9t9u9vwSXC@RBCTx<HGBQ?x<?A@y?BW?IHKBUH<Bz{|}{SC@R@y@BI?RR@AQ?BUH>jHBxT<HAHEOB~Dh>TBUH<B
QTx<TAHABAT<T>T<QTBR=>>?A@>?UH>TPTVHAHBDAT<H>T<HAHEBTy>HVHAQTB?C@R>?h@A@EOBS
9
S
pqrs99u9vw9z{|}{SH>TB?C@RBCTx<HGBQ?x<?A@y?BW?IHKBUH<BQTx<TBR=>>?AG?A@ABh?<?<@BI?RR@AQ?B
G;J;<BWF<FPF>T<HB?C@W@AQ?ABH>HyRHWHAHBQHRR?JTB?>?<?RBUH>jHBxT<HAHEOBFAFGFEQTBR=>>?A@>?AB
WF<FPFBQTx<T>T<HAQTABD<ATR>T<BxT<T<TRBz{|}{SWF<FPFBQTx<T>T<HBH>TBQHVT<BQTx<T>T<HB
R?<y@>?yJ@<?<?RS?C@R>?G?A@E@BjTAHy>TJHAHEOBS
9
S
pqrs99u9vw9Z>TRJ<;AHRBWHGF>?Wh;ABh?E@>@G>?<@BH>TBz{|}{SH>TBjT<CTR>TyJH<H>TABU=BQTx<TAHAB
C@R@y@A@BDAPTBBjH<HyHBHCHABBJ;K<?V?BU?V>@B;>G?RBFET<TBkBBxTBBJTKTBQTVT<HATB
W?IHKBBEB<TR?AW@AQ?RHB?<R>@BJHKJTRHSWHAFWkBR?<TkBgYBxTBFCjTABjH<HyBHy?<TJ>T<HBHCHABxTBQ?I?B
W;A<?BQ?BBjH<HyHBHCHABBJ;K<?V?BU?V>@B;>G?RBFET<TBkBBxTBBJTKTBQTVT<HATBW?IHKBB
EB<TR?AW@AQ?RHB?<R>@BJHKJTRHBWHAFWkBR?<TkBgYBxTBFCjTABjH<HyBHy?<TJ>T<HBHCHABjDE>TG>ThHAHEOB
X>Q@V@A@EBW;A=C>?<@Bh;<=G>?h@A@EOBS
9
S
pqrs99u9vw9BxTBBjH<Hy>T<HAHABIT<BHRHWHAHBJ;K<?V?BU?V>?Q@V@A@EQ?Bz{|}{SC@R@y@A@B
jDE>TG>ThHAHEBT;<HRBxTBK<?JHRBW;A=C>?<@BQHRR?JTB?>@A@EOOBX>Q@V@A@EBW;A=C>?<@Bh;<=G>?h@A@EOBS
9
S
pqrs99u9vw9z{|}{@ABUDh>TB?C@RBCTx<HGBR=>>aA@>G?W@AQ?RHBW@A@<>@R>?<@A@BxTBQTE?x?AJ?>?<@A@B
?C@R>?h@A@EOBXC@R>?G?A@E@B?<R>@BJF<QTRHBxTB?<R>@B<TR?AW>?<Q?RHBjH<HyBHy?<TJ>T<HATB\n\[^mS
QTx<TAHABxT<QHVHBPTx?U@BQHRR?JTB?>?<?RBjTAHy>TJHAHEoS?<R>@B<TR?AW>@BQTx<TBJ?W?<@G>?<@AQ?BA?W@>B
UH<BCDEFGBh;>=BR=>>?A@>?P?V@A@BhDAJTGBxTBR=>>?A@>?P?RBhFRWT>JTCBTAJTj<TBG;QT>BD<ATVHB
xT<T<TRB?C@R>?h@A@EOBS
5q8S:HGF>?Wh;AB;<J?G@AQ?B?<R>@B<TR?AWBJTKRH>T<HATBWHWJTGHABPTx?U@B?hA@BR?U=>BTQH>QHVHBHCHAB
U=BJHKB?A?>HEHBT>TRJ<;AHRBWHGF>?Wh;ABh?E@>@G>?<@BTy>HVHAQTBjT<CTR>TyJH<HAHEOBS
AJT<ATJJTAB?<?yJ@<G?Bh?KG?RBHCHABD<ATVHAB ¡B¢£X¤£BDET>>HR>T<HATBU?RG?RBFET<TB
j;;j>TB?<?G?BG;J;<=A=BR=>>?A?<?RB ¡BxTBQ?J?WITTJB?A?IJ?<BRT>HGT>T<HAHBR=>>?A@A@EOB~=B
yTRH>QTB ¡B¢£X¤£BT>TG?A@A@AB<TR?AWBJTKRHWHAHBxTBI?AjHBJF<BQTx<T>T<QTBR=>>?A@>@KkB
I?AjH>T<HAQTBR=>>?A@>?G?h?P?V@BI?RR@AQ?BUH>jHBJ;K>?h@A@EBxTBCDEFGFAFEFBjTAHy>TJHAHEOBS
012340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=
>
?@AB=C=D=CE=FGHIJKLJHMNOOPQINHR>SNLOTPHUVLGHMNWPLTNXPQPWHYZVLGTNLHWVLHQ[\JT[O\JHVT]NTPIPLHKJH
^_W`]`Q`HMNWPLTN]NXNHaJLJOHXVO\GLbHZVLGTNLHXGONLPINO[TJLIJQHSNLOTPHVTNcNO\PLbHFNU[\HUVLGTNLH
IJdJLTJQI[L]JXJHNTPQ]NXNcNO\PLbe>
6789:;<=
>
>
>
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 4
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.2):
Bilindiği gibi opampların açık çevrim kazancı çok yüksektir. Bu durum kullanıcıya her zaman avantaj
sağlamaz. Çünkü opamp’ın kazanç kontrol altında değildir. Yükselteç tasarımında elemanın kazancı
kullanıcı tarafından kontrol edilmelidir. Opamp kazancının kontrol edilebileceği iki temel tip
yükselteç devresi vardır. Bunlar; eviren (inverting) ve evirmeyen (noninverting) yükselteçlerdir.
Opamp’ın kazancını kontol etmede en etkili yöntem geri besleme kullanmaktır.
OP-AMP 'ın özelliklerinden biri de (+) ve (-) giriş uçlarında potansiyel fark 0 volttur. Çünkü OPAMP 'ların giriş empedansları çok yüksek olduğundan (+) ve {-) giriş uçlarından akan akım pratikte
nanoamper seviyesindedir. Đdeal bir OP-AMP 'ta (+) ve (-) giriş uçlarından akım akmadığı kabul
edilirse, (+) ve (-) giriş uçlarındaki voltaj farkı da sıfır olacaktır. Bundan dolayı OP-AMP 'larda
devreye giren akım, elemana girmez kabul edilir. Şekilde akım yönleri bu kurala göre çizilmiştir.
Kısaca OPAMP'ın bu udurmlarını şöyle özetleyebiliriz:
• Opamp’ın eviren (-) ve evirmeyen (+) girişleri arasında potansiyel fark yoktur. Kısaca gerilim
farkı sıfırdır.
• Opampın eviren (-) ve evirmeyen (+) uçlarından, opamp içerisine küçük bir akım akar. Bu akım
çok küçük olduğundan ihmal edilebilir ve böylece sıfır (0) kabul edilir.
Şekildeki devrede giriş sinyali OP-AMP 'ın (-) ucu olan faz çeviren girişine uygulandığı için devrenin
adı FAZ ÇEVĐREN YÜKSELTEÇ olarak da isimlendirilir. Bu devrede R1 direnci giriş, Rf direnci ise
geri besleme (feedback) direncidir. Girişe AC veya DC sinyal uygulansa dahi bu yükselteç, girişine
uygulanan sinyallerin seviyesine yükseltir, şiddetlendirir. OP-AMP 'a harici dirençler bağlandığı için,
bu yükselteç; açık çevrim kazancından bağımsız bir kapalı çevrim kazancına sahiptir. Kapalı çevrim
kazancı harici olarak bağlanan bu dirençlerin değerine bağlıdır.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 4
Devrede evirmeyen giriş toprağa bağlanmış, giriş işareti R1 direnci ile evirmeyen girişe bağlanmıştır.
Çıkış ile eviren giriş arasına bağlanan RF direnci geri beslemeyi sağlamaktadır. Op-amp’ın gerilim
kazancı çok yüksek olduğundan toprağa bağlı olan evirmeyen giriş, eviren giriş potansiyelinin toprak
potansiyelinde olmasına yol açar.Bu duruma görünür toprak (zahiri toprak) adı verilir. Op-amp’ın iç
direnci çok yüksek olduğundan iç devre üzerinden bir akım akmaz. Bu durumda giriş akımı
geribesleme akımına eşit olacaktır.
Şekildeki R1, giriş direnci ve R2 geri besleme direncidir. OP-AMP 'ın özelliğinden dolayı x
noktasındaki potansiyel 0 volt 'tur. (Vx = 0). Kirchhoff 'un akımlar kanununa göre bir düğüm
noktasına gelen akımların toplamı, giden akıma eşit olduğu için Ii = If 'dir. Dolayısıyla R1 'den akan
akım Rf 'den de akacaktır.
Ii = (Vi - Vx) / R1 (Vx = 0 Volt olduğundan)
Ii = Vi / R1 olur.
If = (Vx - Vo) / Rf (Vx = 0 Volt olduğundan)
If = - (Vo / Rf) olur.
Ii ve If akımları birbirine eşit olduğundan;
Ii = If
(Vi / R1) = -(Vo / Rf) olur. Đçler dışlar çarpımı yaparsak;
-Vo.R1 = Vi.Rf elde edilir.
(Vo / Vi) = -(Rf / R1)
Bu formülde çıkış voltajının, giriş voltajına oranı yükseltecin gerilim kazancını vereceği için;
Av = -(Rf / R1) elde edilir.
Son olarak elde edilen formüldeki (-) işareti giriş ile çıkış arasında 180° faz farkı olduğunu gösterir.
Rf ve R1 dirençleri ile yükseltecin kazancı ayarlanabilir. Bu bağlantıya göre kapalı çevrim kazancı,
ayarlanabilir. Bu bağlantıya göre kapalı çevrim kazancı, açık çevrim kazancından küçüktür. Fakat,
devrenin çalışması, kapalı çevrim kazancından daha kararlıdır. Bu OP-AMP devresinin, geri
beslemeli kazancı, geri beslemesiz kazancından daha küçük olduğu için kullanılan geri besleme
NEGATĐF GERĐ BESLEME 'dir. Pozitif geri besleme olsaydı, geri beslemeli kazanç, geri beslemesiz
kazançtan daha büyük (200.000 'den büyük) olurdu.
Av = -(Rf / R1) formülüne göre eğer Rf = R1 olarak seçilirse yükseltecin kazancı -l 'e eşit olur. Bu
gibi durumlarda, bu yükselteç girişine uygulanan sinyali yükseltmeden sadece polaritesini değiştirerek
çıkışa aktarır.
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 4
Eviren yükselteç devresinde (+) giriş topraklanmış ve giriş (-) girişten verilmiştir.
Böylece giriş ile çıkışın 180° faz farklı olması sağlanmıştır. Burada evirenin anlamı giriş sinyalini ters
çevirmek anlamında kullanılmaktadır. Devre basitleştirilmek amacı ile besleme gerilimleri olmadan
çizilmiştir.
A = - R2/R1 dir.
Buradaki " - " işaretinin anlamı, çıkışın girişe göre evirilmiş hali "inverted" olmasıdır.
Yani, girişe uygulanan sinyal R2/R1 kadar büyütülür, fakat sinyalin işareti giriş sinyalinin tersi olur.
Devrenin giriş direnci;
Rin = e1 / ( ( e1 - e) / R1), eğer "e" sıfır kabul edilirse,
Rin = e1 / e1 / R1,
Rin = R1 bulunur.
Basit bir örnek yapacak olursak, yukarıdaki devrede R2 = 56K ve R1 = 1.2K olursa devrenin
kazancı;
A = - 56 / 1.2
A = - 46,7 bulunur.
Aşağıda konuyla ilgili başka örmnekler verilmiştir.
V1=2V verildiği zaman ve R1=5kΩ, R2=8,7kΩ durumunda;
V elde edilir.
V1=-2V ; R1=5kΩ, R2=8,7kΩ durumunda;
V elde edilir.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 4
V1=5V ; R1=8,7kΩ, R2=5kΩ durumunda;
V elde edilir.
V1=-5V ; R1=8,7kΩ, R2=5kΩ durumunda;
V elde edilir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_02/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567689:;<=<9>?7<@<A9BCDEFGEDHIJKGEDLEMHNOPQRPSHLEFEDHTEUEIDEVBW
5676897?9A9XYZY99
567689>?7<@<9A9[\]^_`abcde_fg_h9
567689ijiklA99
Xm9OPQRPnopHqrstqpHustsvHwxwpyHwzuw{ypypH|spzy{spH}o~ovyHHy
Hyt~{oH{wwpwH
W
ZmWOPQRPW~y
ypxoHtypopyHz~|q{sspspHs|yopopHuqt}q~{qvstqs{q~HW
mWqtsHq|{qq{sHstH|s|qsHKVVDDKHy}o|opypHztw{yzys{q~W
56768966ji7i;lA99
HyqHHFHHyqHHKHyp|szqtqW
[¡[ba¢£¤¥¦¢§¢¨¤©a9
ªwHqpqzHs{qHs{us{sHqts~HrqHyztopo{oHs{us{qtHs}spH«qHyyp{oH|s{y|zpHwzuw{yy|oH
s~¬poH|wpypH­GEGH|s|qsH«qHy{ypo|opyHw{yvy~H
qtqH®¯°̄±²²³³³´µ¶¯µ·³µ·¸¯²W
³¹ºW¸¹»¼¶¼W½¼¾¹W̄¹¸¹º¼·¼»¼¶¼½WW
567689̈¿§À¦¢¨bÁ¡ÂA99
ªwHqpqzHs}spH«qHyyp{oH|s{y|zpHwzuw{yy|oHs~¬poH|wpypH­GEGH|s|qsH«qH
y{ypo|opyHw{yvy~Hs}spH®¯°̄±²²³³³´µ¶¯µ·³µ·¸¯²W³¹ºW¸¹»¼¶¼W½¼¾¹W̄¹¸¹º¼·¼»¼¶¼½WW
567689i5lji;lA99
XmWCq~s{q~sHqrtqzsH~wtwpw
HW W
ÃÄÅÃÆ/ ÇÄÅÈÉÆ/ ÇÊÅÈÉÆ/ ÃËÅÃÆ/
Ê/ Ì/ ÄË/ /
ÍÊ/ Ì/ ÄË/ /
Ì/ ÄË/ Ì/ /
ÍÌ/ ÄË/ Ì/ /
W
W
ZmWIw~ytoy~sWy{zyHuÎtqHÏHÎ{}{qtspsHzyyty~Hy{zyH~yzqsps
HÏH|spzy{spspH
svytqspspHqsvsspsHNqrts{sspsSHrqHz~|q{s{sspsÐvt{pHuÎ
{q{qzsps
HrqH
|pw}{ytopo
oHztw{yzopo
HW
mWzpoHÎ{}{qtsHÏHustsvspqWÑÏHqqHqqtspqH|yÒsHÑWÓÔ½Õ·¼WQÖWsvy¹W̄×¾Ø×·¾W
uqt}q~{qvstsps
HrqH|pw}{ytopo
oHztw{yzopo
WÙ7ÚÛAWEqtHwHyoyHs|qps{qpHuqp{s~H
qqtspqHstHsvytqHrqtszt|yH|spzy{HÜqpqtyÎtpqpHq{qHqs{qpH|spzy{spHs|qps{qpHuqp{s~H
0112340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;7<;=>?@<A7B:9:@7C:@7D78:;7<E7;6:;:F<GHFIJ<A7B:9:;:FK<LM9;78:;<CN<H9;7EB7<OP<B7Q7<67879:<
R<PS@B<B7Q767;<B7Q7T7<678797<>=U:Q<>:;T=@:<AH>B79J7EB76:9K<V=;:<>:;T=@<W7;79=BH9I;67;<7879<O<
PS@B<67879:;67;<=F<X7T=<O<PS@B<67879:;67;<Y=F@=<C:9<A7;@:E<67879:<E:<CN<67879<S@=<E:<D:U=F6=;<
:>B7;:@7;<O<PS@B<67879:;7<=T=9@=;=J?TS9<S@>N;Z<CN<6N9NJ=<;=>?@<C:9<GHFIJ<NTAN@=9>?;?F[\]^
^
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
^
_`abcda^efghgijklmno^^
p
h`qo^rS9N@=9?;<GHFIJI<:G:;<UBBQsttuuuKDS;B9S@uS9@6KBEt<pu7C<C=8@=;B?>?;6=;<vwrxr<
yzy{|}z~|pz{pp|~|z~p
7;7T<TAN@=J=>?<CH@IJI;I<~9=E<T=96?J<=@=C:@:9Z<67;7T<
U=EE?;6=<=T9?;B?@?<B7S9:E<C:@A:<:G:;<67<T:;7<=T;?<>:>B7J:;<CN<67;7T7<=:B<B7S9:E<C:@A:<CH@IJI;67;<
~zzyz~z]pp
p
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:9;9<=9>?@ABCDEFD>G@?HBCDIJKLMDNOFPFDQ?DRSRTLDGDUODVPFMLTWXTYLDGHDQDZF[FD
YF\FP]TFDWL^][DW]TNWD]_LPFZ]D̀NabFTDMLPFDYLJbLDEFDcdDW]TeLJDRebRJLeXTXODEFDaXMX_XD
bfOJFKJFe]T]OgDhJYX\XTXODWITRaJLPXDeIPRKJLeXTXOgDi
jklmnop9
i
56789q9;9<=9>?@ABCDEFD>G@?HBCDIJKLMDNOFPFDQ?DRSRTLDWXPLWXeJLDAQD̀?HDQDEFDGHQDZF[FD
YF\FP]TFDWL^][DcdD]_LPFZDRebRJLeXTXODEFDaXMX_XDbfOJFKJFe]T]OgDhJYX\XTXODWITRaJLPXD
eIPRKJLeXTXOgDi
jklmnop9
i
56789r9;9<=9Q?Db]P]_DW]TeLJ]DADQDbFTJ]MJ]D?HDUODVPFMLTWXTYLDIJKLMDNOFPFD>?DYF\FP]DWLs]ZDIJKLMD
NOFPFD>G@Gt>?D̀>G@ut>?DEFD>G@vt>?DIJLSLMD_FM]JYFD>GDYF\FPJFP]TYFDwxyzxiaXMX_XTXD
bfOJFKJFe]T]OgDhJYX\XTXODWITRaJLPXDeIPRKJLeXTXOgDi
jklmnop9
i
56789{9;9<=9|E]PFTDeNMWFJZFaDYFEPFJFP]T]TDTFPFJFPYFDEFDTFDLKLaJLDMRJJLTXJYX\XTXDLaXMJLeXTXOgD
haXMJLKLTXOXDfTFP]JFP]T]ODF_J]\]TYFDbFT]_JFZ]T]OgDi
jklmnop9
i
56789}9;9<=9~LPMJXDZNPYFM]DFE]PFTDeNMWFJZFaDYFEPFJFP]TFDfPTFMJFPDEFPFPFMD^FPis]P]T]DLaXMJLeXTXOgDi
jklmnop9
i
56789<9;9<=9RDYFEPFD^LMMXTYLDiVLPMJXDWIPRD^LOXPJLeXTXODIPRJLPDOIPDT]ZFJ]MZFDIJKLJXYXPDEFD
afONKNTND^LOXPJLKLeLDbFPFMDeIMZRPgDIPRJLPDeRMLPXYLM]JFPYFTDVLPMJXDIJLSLMZXPgDLW]ZDWIPRJLPD
YF\FPJFTY]PKFeFDLJXTKLeLSLMZXPgi
jklmnop9
i
i
i
0123420
TEORĐK BĐLGĐ
Sayfa 1 / 5
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.3):
Opampların temel uygulamalarından bir diğeri ise evirmeyen yükselteç devresidir. Bu devrede
yükseltilecek işaret opamp’ın evirmeyen girişine uygulanmaktadır. Evirmeyen yükselteç devresinde
giriş işareti ile çıkış işareti aynı fazdadır. Yani giriş ile çıkış işareti arasında faz farkı yoktur. Temel
bir evirmeyen yükselteç devresi aşağıdaki şekilde verilmiştir.
Evirmeyen yükselteç devresinin en önemli özelliklerinden birisi çok yüksek bir giriş direncine sahip
olmasıdır. Eviren bir yükselteç devresinde giriş direnci, devrede kullanılan R1 direncine bağlıdır ve
değeri birkaç ohm civarındadır. Evirmeyen yükselteç devresinde ise giriş direnci opamp’ın giriş
direncine eşittir. Bu değer ise yüzlerce mega ohm civarındadır.
OPAMP'ın eviren ucu ile evirmeyen ucu arasındaki potansiyel fark 0V olduğundan R1 direnci
üzerinde giriş gerilimi görülecektir. Bu durumda giriş akımı ile geri besleme akımı (bir üstteki şekile
de dikkat edilirse) birbirine eşittir (I1=If). Bu durumda
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 5
olacaktır. Ayrıca, burada evirmeyen yükseltecin çıkışındaki sinyalin işareti girişi ile aynı yöndedir.
Yukarıdaki devrede genel gösterime göre OPAMP elemanının pozitif ve negatif uçlarının yerlerinin
gösterimsel olarak değiştirildiğine dikkat ediniz. Bu devrede "e" gerilimi işlemsel yükseltecin giriş
direncinin çok yüksek olmasından dolayı 0V varsayılır. Bu durumda R2 ve R1 dirençlerinin birleştiği
"A" noktasındaki gerilim değeri "e1" giriş gerilimine eşit olur. Zaten işlemsel yükseltecin yada bu
devrenin giriş empedansı çok yüksek olacağı için e1 gerilimi veya "A" noktasındaki gerilim işlemsel
yükseltecin içine bir akım akıtamaz. Bu nedenle R2 üzerindeki akım R1 üzerindeki akıma eşittir.
Bunları formüllerle yazarsak;
i1 = (e2 - e1) / R2
i2 = e1 / R1
i1 = i2
(e2 - e1) / R2 = e1 / R1
Gerilim kazancı A;
e2 / e1 = (R1 + R2) / R1
e2 / e1 = 1 + ( R2 / R1),
A = 1 + ( R2 / R1) olarak bulunur.
Çeşitli örnekler yapalım.
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 5
1- Yukarıdaki şekilde R2 = 56K ve R1 = 1.2K olsun. Devrenin kazancı;
A = 1 + ( R2 / R1)
A = 1 + ( 56 / 1.2)
A = 47.7 olarak bulunur.
2- Yukarıdaki şekilde R2 = 0 "kısa devre" ve R1 = sonsuz "açık devre" olsun. Kazanç;
A = 1 + ( R2 / R1)
A = 1 + ( 0 / ∞)
A = 1 olur.
Zaten, bu şekildeki devre aslında bir gerilim izleyicidir. Yada başka bir deyişle, evirmeyen yükselteç
gerilim izleyicinin genel halidir.
3- Aşağıdaki şekildeki evirmeyen yükselteç devresinde çıkış gerilimi (Vout) ve gerilim kazancını
hesaplayalım. .
Çözüm:
Çıkış geriliminini hesaplarsak,
şeklinde olacaktır. Şimdi ise gerilim kazancını hesaplayalım.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 5
Gerlim kazancı da görüldüğü üzere 6 olarak bulunur.
Başka bir örnek ile grafiksel olarak bu uygulayı inceleyelim. Aşağıdaki örneğe bakalım. Normalde
OPAMP çıkış denklemlerini hatırlayalım. Aşağıdaki evirmeyen yükselteç kazancı için aşağıdaki
denklemleri kullanırız.
Opamp’ın kazancı; k= 1+(R2/R1)
Opamp çıkış gerilimi V0=k*V1
1. VAC= 2,05V
R2=10KΩ R1=10 KΩ Đse; Opamp’ın kazancı yukarıdaki kazanç
formülünden hesaplanırsa k= 2 olur.
V1= 1 Kare 1V
V0=> 1 kare 2V
Bir başka örnek ile de konumuza daha ayrıntılı açıklama getirebiliriz. Aşağıdaki her bir örneği
dikkatle inceleyiniz.
1. V1=2V verildiği zaman ve R1=10kΩ, R2=10kΩ durumunda;
V elde edilir.
2. V1=-2V ; R1=5kΩ, R2=10kΩ durumunda;
V elde edilir.
3. V1=5V ; R1=10kΩ, R2=5kΩ durumunda;
V elde edilir.
4. V1=-5V ; R1=10kΩ, R2=10kΩ durumunda;
V elde edilir.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 5
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_03/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDEFGHFEIJKLHFEMFNIOPQRSQTUVWSWXUYFZFJEF[CU
67879:8@:B:\]^]::
67879:?@8=A=:B:_`abcdedfghijkdlmdn:
67879:opoqrB::
\sUPQRSQtuvIwxyz{w|wvI}yzy~IvI|}vvIyv|yvIu
u~IIz
uIvI
U
sUPQRSQU
vuIzvuvI|
wyyvyvIyuvuvI}wzw
w~yzwy{w
IU
^sUwzyIww{wyIyzIyw{yIL[[EELIuuvvI|z{|y{w
U
67879:77po8o<rB::
IwIIG I¡IwI¢IL£Ivy|{wzwU
¤_¥_hg¦§¨©ª¦«¦¬¨­g:
®Iwvw|IywIy}yyIwzy
IxwI|zuvuuIy}ywzIyyvI¯wIvuIy{|vI|}{uI
y{
°vuIvvI±HFHIyw{yI¯wIvuuvI~{
IwzwI²³³́µ¶¶···¸¹º³¹»·¹»¼³¶U
·½¾U¼½¿ÀºÀUÁÀ½³U½¼½¾À»À¿ÀºÀÁUU
67879:¬Ã«Äª¦¬hÅ¥ÆB::
®Iwvw|IyyvI¯wIvuIy{|vI|}{uIy{
°vuIvvI±HFHIyw{yI¯wI
vuuvI~{
IyyvI²³³́µ¶¶···¸¹º³¹»·¹»¼³¶U·½¾U¼½¿ÀºÀUÁÀ½³U½¼½¾À»À¿ÀºÀÁUU
67879:o6rpo<rB::
\sUDw
yw
yIwxzw|yI
zvÁUU U
U
ÇÈÉÇÊ/ ËÈÉÌÍÊ/ ËÎÉÌÍÊ/ ÇÏÉÇÊ/
Î/ ÈÏ/ ÈÏ/ /
ÐÎ/ Ñ/ ÈÏ/ /
Ñ/ ÈÏ/ Ñ/ /
ÐÑ/ ÈÏ/ ÈÏ/ /
U
sUJv
yI|I}ÒzwIÓIÒ{wzyvyI|z
I|I
|wyvyIÓIyv|yvyvIy~zwyvyvI
wy~yyvyIOwxzyyyvyÔIxwI|
wyyyvyÕ~zvI}Òw{w|yvyIxwIvzuvuuI
|z{|uvuIU
^sU|vuIÒ{wzyIÓI}yzy~yvwIÖÓIwwIwwzyvwI×yIÖUØÙÁÚ»ÀURÛUy~zwIÜÂÝÜ»ÂU
}wzw
w~yzyvyIxwIvzuvuuI|z{|uvuUÞ8ßàBUFwzIIu{IywvywvI}wvy
I
wwzyvwIyzIy~zwIxwz{y|zIyv|IáwvwzÒzvwvIwwIwywvIyv|yvIywvywvI}wvy
I
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;7<;=>?@<A7B:9:@7C:@7D78:;7<E7;6:;:F<GHFIJ<A7B:9:;:FK<LM9;78:;<CN<H9;7EB7<OP<B7Q7<67879:<
R<PS@B<B7Q767;<B7Q7T7<678797<>=U:Q<>:;T=@:<AH>B79J7EB76:9K<V=;:<>:;T=@<W7;79=BH9I;67;<7879<O<
PS@B<67879:;67;<=F<X7T=<O<PS@B<67879:;67;<Y=F@=<C:9<A7;@:E<67879:<E:<CN<67879<S@=<E:<D:U=F6=;<
:>B7;:@7;<O<PS@B<67879:;7<=T=9@=;=J?TS9<S@>N;Z<CN<6N9NJ=<;=>?@<C:9<GHFIJ<NTAN@=9>?;?F[\]^
^
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
_
`abcdeb_fghihjklmnop__
^
iaqp_rS9N@=9?;<GHFIJI<:G:;<UBBQsttuuuKDS;B9S@uS9@6KBEt<^u7C<C=8@=;B?>?;6=;<vwrxr<
yzy{|}z~|^z{^^|~|z~^
7;7T<TAN@=J=>?<CH@IJI;I^~9=E<T=96?J<=@=C:@:9Z<67;7T<
U=EE?;6=<=T9?;B?@?<B7S9:E<C:@A:<:G:;<67<T:;7<=T;?<>:>B7J:;<CN<67;7T7<=:B<B7S9:E<C:@A:<CH@IJI;67;<
~zzyz~z]^^
^
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;:<:=>:?@ABCDEFGE?HA@ICDEJKLMNEOPGQGER@ESTSUMEHEVPEWQGNMUXYUZMEHIERE[G\GE
ZG]GQ^UGEXM_^\EX^UOXE^`MQG[^aEObcGUENMQGEZMKcMEFGEdeEX^UfMKESfcSKMfYUYPEFGEbYNỲYE
cgPKGLKGf^U^PhEiKZY]YUYPEXJUSbKMQYEfJQSLKMfYUYPhEj
klmnopq:
j
6789:r:<:=>:?@ABCDEFGE?HA@ICDEJKLMNEOPGQGER@ESTSUMEXYQMXYfKMEBRaE@IEREFGEHIRE[G\GE
ZG]GQ^UGEXM_^\EdeE^`MQG[ESfcSKMfYUYPEFGEbYNỲYEcgPKGLKGf^U^PhEiKZY]YUYPEXJUSbKMQYE
fJQSLKMfYUYPhEj
klmnopq:
j
6789:s:<:=>:R@Ec^Q^`EX^UfMK^EBEREcGUK^NK^E@IEVPEWQGNMUXYUZMEJKLMNEOPGQGE?@EZG]GQ^EXMt^[EJKLMNE
OPGQGE?HAHu?@aE?HAvu?@EFGE?HAwu?@EJKMTMNE`GN^KZGE?HEZG]GQKGQ^UZGExyz{yjbYNỲYUYE
cgPKGLKGf^U^PhEiKZY]YUYPEXJUSbKMQYEfJQSLKMfYUYPhEj
klmnopq:
j
6789:|:<:=>:}F^QLGfGUEfONXGK[GbEZGFQGKGQ^U^UEUGQGKGQZGEFGEUGEMLMbKMENSKKMUYKZY]YUYE
MbYNKMfYUYPhEibYNKMLMUYPYEgUGQ^KGQ^U^PEG`K^]^UZGEcGU^`KG[^U^PhEj
klmnopq:
j
6789:~:<:=>:MQNKYE[OQZGN^EGF^QLGfGUEfONXGK[GbEZGFQGKGQ^UGEgQUGNKGQEFGQGQjj
j
MbYNKMfYUYPhEj
klmnopq:
j
6789:=:<:=>:SEZGFQGE_MNNYUZMEvEWMQNKYEXJQSE_MPYQKMfYUYPEJQSKMQEPJQEU^[GK^N[GEJKLMKYZYQEFGE
bgPOLOUOE_MPYQKMLMfMEcGQGNEfJN[SQhEJQSKMQEfSNMQYZMN^KGQZGUEWMQNKYEJKMTMN[YQhEMX^[EXJQSKMQE
ZG]GQKGUZ^QLGfGEMKYULMfMTMN[YQhj
klmnopq:
j
j
j
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 2
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.4):
Temel eviren yükselteç devresindeki negatif terminale tek giriş yerine, bir
çok giriş işareti bağlanırsa opamp eviren toplayıcı olarak çalışır. Eviren toplayıcı devre,
girişine uygulanan işaretleri toplayarak çıkışına aktarır.
Eğer giriş gerilimleri sırası ile; V1, V2 ….. Vn ise; ortak uç (negatif terminal) toprak
potansiyelinde olduğu için opamp’ın + ile - terminalleri arasında potansiyel fark yoktur.
Dolayısı ile her bir koldan akan akımlar sırası ile;
olur. RF geri besleme direncinden bu akımların toplamı kadar bir akım akacağından
(opampın içine akım akmaz, giriş direnci sonsuzdur). Bu durumda opamp’ın çıkış gerilimi;
Opamp’ın kazancı; k= -(R2/R1) formülü ile V1 ,V2 , V3 kaynaklarına seri bağlı dirençlere bağlı
olarak opamp kazancı hesaplanır. Bu deneyde direnç değerleri aynı olduğu için ve girişler eviren
uçtan yapıldığı için kazanç k daima negatif olacaktır.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_04/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 2
Opamp çıkış geriliminin genel ifadesi; V0= -(k1*V1 + k2* V2 + k3*V3) ile hesaplanır. k
değerimiz 1 çıktığı için çıkış gerilimi giriş gerilimlerinin toplamıdır. Ancak giriş sinyali ile çıkış
sinyali arasında 180° faz farkı oluşur.
V1AC=3.3V , V2ac=2.9V , V3ac=1.2V Girişleri opamp’a uygulandığında V0 çıkış gerilimi yukarıda
belirtilen Opamp çıkış gerilimi formülünden hesaplandığında çıkış geriliminin -7.9V olduğu
görülmektedir. Aşağıdaki grafikte giriş ve çıkış gerilimlerinin osilaskoptaki grafikleri görülmektedir.
Grafik için; 1 kare 2V’a karşılık gelmektedir.
DEĞERLENDĐRME
Yukarıdaki denklemden fark edileceği üzere farz çeviren toplama devresi birden çok faz çeviren
kuvvetlendiricinin birleşimi gibidir. Superposition ilkesi kullanılarak bu faz çeviren
kuvvetlendiricilerin çıkışları toplandığında da aynı sonuç elde edilir.
Devredeki bütün dirençlerin eşit olması durumunda ise tahmin edileceği gibi her bir faz çeviren
kuvvetlendiricinin kazanç katsayısı -1 olacağından V0, giriş işaretlerinin toplamının eksilisidir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_04/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567689:;<=<9>?7<@<A9BCDEFGEDHIJKGEDLEMHNOPQRPSHLEFEDHTEUEIDEVBW
5676897?9A9XYZY99
567689>?7<@<9A9[\]^_`_95abcade9
567689fgfhiA99
Xj9OPQRPklmHnopqnmHrpqpsHtutmvHtwrtxvmvmHypmwvxxnqpmHOPQRPWzl{lslm|vH{nm|pxnqpm|nmH}~HH
vHvq{xlHxvqv{Hwvmyllx|l
lmlH{voqvv{HW
j9OPQRPW{vvmulHqvmlm|vHrpqpsHpsvqnxnqpmpmHzl{lsvHxvm|l
lmlHpyvxvv{W
56768966gf7f;iA99
}Hv|nH}HFHHv|nH}HKHH}Hv|nHHH}Hv|nHHH}Hv|nH}HKW
567689f9
tH|nmnwHpxnHpxrpxpHnqp{HonHvwqlmlxlHpxrpxnqHpzpmH nHvvmxlHyp¡xvywmHtwrtxvvylH
p{¢mlHytmvmH£GEGHypynpH nHv
xvmlylmvHtxvsv{H¡nqnH¤¥¥¦§¨¨©©©ª«¬¥­«®©«­®¯¥°Ẅ
©±²W³¯­±´µ¬µW¶µ·³­±¥W±¯±²µ®µ­´µ¬µ¶WW
567689¸¹º»¼½A99
tH|nmnwHpzpmH nHvvmxlHyp¡xvywmHtwrtxvvylHp{¢mlHytmvmH£GEGHypynpH nH
v
xvmlylmvHtxvsv{HpzpmH¤¥¥¦§¨¨©©©ª«¬¥­«®©«­®¯¥°Ẅ©±²W³¯­±´µ¬µW¶µ·³­±¥W±¯±²µ®µ­´µ¬µ¶WW
567689f5igf;iA99
XjWCn{px|n{pH|noqnwpH{tqtmtHW W
W
¾¿À¾Á/ ¾ÂÀ¾Á/ ¾ÃÀ¾Á/ ¾ÄÀ¾Á/
/ / / /
W
jWÅ}HÅÆHÅHonHÅHrnqpxpxnqpmpHÇxz¡m¡HonHvxwvH{vw|n|pmpHÅÈÅ}ÉÅÆÉÅHx|t
tmtH
rÇxnxnwpmpHonHymtutmttHwqtxvwlmlHW
ÊjWËnqpxpHÇx¡u¡Hxvqv{H{txxvmlxvmH|pqnmzxnqpmHÌ}HÅHÍHxt{HnyxnnypHwnqpmnHm{ypwmH
ÎnmnqvÇq¡m|nmHÏÐÅHnnH|n
nqpmnHyvÑpHÒÐÐWÓ¶Ô®µ°WQÕWpsvqnHÖ·×Ö®³·³­³°ØW«´µ®³´°«¦®³WÙÒØW
ÅÆHÅHonHÅHÍHmlmH|n
psppmpHpmunxnwpmpHvxHvxvHzppmpHonHymtzxvqlmllHwqtxvwlmlWWÚ7\ÛAW
E
nqHtHv|l|vHpynmpxnmHrnmxp{H|n
nqpm|nHpqHpsvqnHonqpwqyvHypmwvxHÎnmnqvÇq¡m|nmHnx|nH
n|pxnmHypmwvxpmHpynmpxnmHrnmxp{H|n
nqpmnHmvylxHrnpqpxnpxnun
pmnH{nm|pmpHzǡHrnpqpmpH
NÜqmn
pmHtHÇqmn{nH}ÅHnnH|n
nqpHÆHÅxHnn|nmHnnwnH|n
nqnHyvÑpHypmwvxpH
rÇynqn{n|pqHIvmpHypmwvxHÎnmnqvÇq¡m|nmHn
nqH}HÅxH|n
nqpm|nmHvHonwvH}HÅxH|n
nqpm|nmH
0123240
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67897:;<=:>?@9<A:B?C?=<:A<:;D:B?C?=:E97:A<:F<G78B7@:<HI?@<9?@:J:KE9I:B?C?=<@?:7L7=97@7MNLE=:
E9HD@O:;D:BD=DM7:@7HN9:;<=:PQ8RM:DL>D97=HN@N8STUV
V
W
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
W
XYZ[\]ZW^_`a`bcdefghWW
V
aYihWjE=D97=N@:PQ8RMR:<P<@:GIIklmmnnnoFE@I=E9nE=9BoIAm:Vn?;:;7C97@INHN@B7@:pqjrj:
stsuvwtxvVytuVz{V|vxv}txV~?@?L:L>D97M7HN~:;Q9RMR@R:AD997@7=7A:L7=BNM:797;<9<=O:B?@?L:
G7AAN@B7:7L=N@IN9N:I?E=<A:;<9><:<P<@:B?:L<@?:7L@N:H<HI?M<@:;D:B?@?L?:7<I:I?E=<A:;<9><:;Q9RMR@B?@:
}yyyxyzttstxtUVV
V
X
WdWWcW?=?B?A<:>?=<9<M:;Q9RFR:B<=?@P9?=<:H<MR97IQ=:E=I7MN@7:B7G<9:?B<9M?M<I<=o:J:K:
vVJ:K:><=<:;?H9?M?:A7L@7A97=N:L?=<@?:KO:JK:?:J:K:I?k?:B?C?=<@?:H7G<k:qO:A7=?O:
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<9;=>:6=;=>:?@AA9B>;C?8CA@:DEFE:D@;GHI;GJ;<9;GK;C7A@BE:@;D6L9M9N;89B>A>O;=9<>?9=>:PQ
R9=@SA@?E:ETU;V9=@SA@DEFE:ET;D9F9BA9B9;8WB9;=>O6A@XWB;YBX@OE:D@;GHI;GJ;<9;GKZ6:;8B@[>NA9B>:>;
7>TD>B>:>TU;V9=@SA@O@;>LA9OA9B>:>;@7ENA@?E:ETU;Q
\]^_`abc
Q
defgchcicjkcGH;CMC:@;J;VT;[B9N@:=E:D@;Hl;G;X9S9;D9F9B>:9;=@R>S;=>:6=;>L@B9X>I;GJ;CMC:@;m;VT;
[B9N@:=E:D@;J;G;X9S9;D9F9B>:9;=@R>S;N@B9;D@A8@;<9;GK;CMC:@;n;VT;[B9N@:=E:D@;o;G;X9S9;
D9F9B>:9;=@R>S;N@B9;D@A8@;<9;C?8CA@?E:ET;<9;7ENELE;8WTA9OA9?>:>TU;pADEFE:ET;=Y:C7A@BE;
?YBCOA@?E:ETU;Q
\]^_`abc
Q
defgcqcicjkcr@BNAE;X6BD9N>;XYSA@O@;D9<B9A9B>:9;WB:9NA9B;<9B9B9N;R9BQsPtPu>;@7ENA@?E:ETU;Q
\]^_`abc
Q
defgcvcicjkcwW?A9;x>B;XYSA@O@;D9<B9=>:D9N>;Hl;yz;D9F9B>:9;=@R>S;D>B9:7A9BI;@?:E;D9F9B9;=@R>S;
[@N@X;[@BNAE;D9F9BD9;D>B9:7A9BA9;?9B;D9F>LX>B>A>B=9;{|}~|Q7ENELE:E:;:@=EA;9XN>A9:9M9F>:>;
9A9NXBY:>N;=>O6A@=?Y:;?@TEAEOA@BE;NCAA@:@B@N;@7ENA@?E:ETU;Q
\]^_`abc
Q
defgccicjkcYSA@O@;D9<B9A9B>:>:;:9B9A9BD9;<9;:9;@O@7A@;NCAA@:EADEFE:E;@7ENA@?E:ETU;
p7ENA@O@:ETE;W:9B>A9B>:>T;9LA>F>:D9;89:>LA9X>:>TU;Q
\]^_`abc
Q
defgcjcicjkcwC;D9<B9;R@NNE:D@;KQ[@BNAE;=YBC;R@TEBA@?E:ET;YBCA@B;TYB;:>X9A>NX9;YAO@AEDEB;<9;
7WT6O6:6;R@TEBA@O@?@;89B9N;?YNXCBU;YBCA@B;?CN@BED@N>A9BD9:;[@BNAE;YA@M@NXEBU;w@=>X;=YBCA@B;
D9F9BA9:D>BO9?9;@AE:O@?@M@NXEBUQ
Q
Q
Q
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 4
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.5):
Bazen iki farklı sinyal arasında istenen bir sinyal elde etmek istenilir. Şüphesiz, bir analog çeviriciden
elde edilen olası tek sinyal ve toplam iki sinyal vardır. Hâlbuki belki daha kolay aynı sonucu başarma
yolu vardır.
Fark alıcı devre, genelde ölçme ve kontrol sistemlerinin tasarımında kullanılan temel yükselteç
devresidir. Oldukça hassas ve kararlı bir çalışma karakteristiğine sahiptir.
Temel fark alıcı devre, çıkarıcı amplifikatör (differance amplifier) veya farksal yükselteç
olarakda isimlendirilir. Temel bir fark alıcı devre dikkatlice incelendiğinde opamp’ın her iki girişinin
de kullanıldığı görülmektedir. Devrenin temel çalışma prensibi eviren ve evirmeyen girişlerine
uygulanan işaretlerin farkını almasıdır. Bu tip yükselteçler pek çok endüstriyel uygulamada sıklıkla
kullanılırlar.
Opamp devresinin fark alma (çıkarma) işlemini , girişten uygulanan iki ayrı işaretin farkı alınıp çıkışa
aktarılması ile gerçekleştirilir.
Devre şekilde görüldüğü gibi normal eviren yükselteç ve evirmeyen yükseltecin olduğu kombineden
oluşmaktadır. Đki Rf ve iki Rin direncinden oluşan bir kuyuyu andırıyor devre. Doğru devre işlemi
için, o iki çiftin uygun bir şekilde birleştirilmesi önemlidir. Devre ile görüldüğü gibi, çıkış voltajının
bağıntısı:
Vout = Rf(V2 - V1)/Rin
Uygun değerler seçilerek bu devrede Vo=V2-V1 çıkışı alınabilir (Yani tüm direnç değerlerinin aynı
değerde seçilmesi durumu göz önünde bulundurulduğunda).
Bu devre doğru ve yanlışsız işlem yapar, ama bir sınırı vardır. "-" giriş sinyalinde çoklu toplama için
kullanılamıyor, çünkü görünürde topraklamada giriş yeterli uzunlukta değil. Devrede ek giriş
sinyalinin eklendiği noktada diğer her bir sinyal ile bu noktada etkileşecek ve çarpıtılmış sonuçlar
üretilecektir.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_05/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 4
V0= (R3+R4)/R3)*[(R2*V1/(R1+R2)-(R4*V2/R3+R4)] Çıkış gerilimi bu formülle hesaplanır.
Yukarıdaki çıkarma devresinde R1 , R2 , R3 , R4 değerleri eşit olduğu için V0=V1-V2 ile hesaplanır.
Gerilim bölücü olarak kullanılan dirençlerin ±15V’luk besleme yerine AC 5V, 50Hz lik sinyal
uygulandığında osilaskopta aşağıda belirtilen dalga şekilleri gözlenmiştir.
1 kare 2V’ karşılık gelmektedir.
DEĞERLENDĐRME
Devreyi bölüm bölüm analiz edelim. Đşlemsel kuvvetlendiricinin pozitif girişindeki gerilim R2 ve R3
dirençleri gerilim bölücü olarak düşünülürse aşağıdaki gibi bulunur.
[1]
Faz çeviren kuvvetlendiriciye benzer olarak aşağıdaki yolla da çıkış geriliminin V1 ve Vn gerilimleri
cinsinden ifadesi bulunur.
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_05/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 4
[2]
[3]
Đşlemsel kuvvetlendiricinin girişlerindeki gerilimlerin eşit olduğunu kabul edersek aşağıdaki eşitlik
ortaya çıkar.
[4]
Elde edilen Vn değeri 3 denkleminde yerine konursa Vo geriliminin giriş gerilimleri ve dirençler
cinsinden ifadesi yazılır.
[5]
Devredeki R1,R2,R3 ve R4 dirençleri eşit olduğunda tahmin edileceği gibi işlemsel
kuvvetlendiricinin çıkış gerilimi pozitif girişi ile negatif girişinin farkı olur.
[6]
Wheatstone Köprüsü:
Bilinmeyen dirençler, Wheatstone köprüsü denen bir devre yardımıyla bulunabilmektedir. Ayrıca,
böyle bir devre endüstride bir algılayıcı elemanın direnç değişiminin gerilim değişimine
çevrilmesinde de kullanılabilir.
Wheatstone köprüsü, şekildeki gibi bilinen R1, R2 dirençleri,
ayarlı RA direnci ve bilinmeyen RX direnci ve A ampermetresinden
oluşur.
Bu devrede RA ayarlı direnç değiştirilerek A ampermetresinin
ölçtüğü akımın sıfır olması sağlanır. Yani K noktasından L ye
ya da L den K ya akımın geçmemesi sağlanır. Bu durumda K ile
L noktalarının potansiyelleri eşit olur. Yani K ile L arasında potansiyel
farkı olmaz. R1 in üzerindeki gerilim RX e, RA nın gerilimi
de R2 ye eşittir. Buna göre,
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_05/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 4
i1.R1 = i2.RX
i1.RA = i2.R2 olduğundan bu iki denklem oranlanırsa,
R1.R2 = RX.RA olur.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_05/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDEFGHFEIJKLHFEMFNIOPQRSQTIMFGFEIUFVFJEFWCX
67879:8@:B:YZ[Z::
67879:?@8=A=:B:\]^_`ab_cdef`egh:
67879:ijiklB::
Ym:PQRSQnopIqrstqpIustsvIwxwpyIwzuw{ypypI|spzy{{qtspIPQRSQX}o~ovopyI~qps{qtspqpIII
y
Iyt~{oI{yty~Izyp|oo{oopoI~yrtyy~IX
mXPQRSQX~y
ypxoItypopyIustsvIsvytq{qtspspI}o~ovyIststspqpIyt~oIy{opoopoIs|y{yy~IX
mXqy|pqI~t|ppIpy|o{I{wvwwpwIrqIpqIyy}{yI~w{{ypo{oopoItqpq~IX
mXstIyyIy{uo{yyIqrtq|sI{yty~I}o~ytyIqrtq|spsIypoy~IrqIqy|pqI~t|Is{qI
s{sv~sI~wtys{q~X
67879:77ji8i<lB::
IyqIIGIIyqIILIIIyqIILIIyqIIIIyqIIL X
6¡¢¡£c¤\¥¦§¤¨¤©¥ªc:
wIqpqzIs{qIs{us{sIqts~IrqIyztopo{oIs{us{qtIs}spI«qIyyp{oI|s{y|zpIwzuw{yy|oI
s~¬poI|wpypI­HFHI|s|qsI«qIy{ypo|opyIw{yvy~I
qtqI®¯°̄±²²³³³ ́µ¶¯·µ³̧µ·¹̧ ̄º²X
³»¼X½¹·»¾¿¶¿XÀ¿Á½·»X̄»¹»¼¿¸¿·¾¿¶¿À XX
67879:©Â¨Ã§¤©£Ä¢ÅB::
wIqpqzIs}spI«qIyyp{oI|s{y|zpIwzuw{yy|oIs~¬poI|wpypI­HFHI|s|qsI«qI
y{ypo|opyIw{yvy~Is}spI®¯°̄±²²³³³ ́µ¶¯·µ³̧µ·¹̧ ̄º²X³»¼X½¹·»¾¿¶¿XÀ¿Á½·»X̄»¹»¼¿¸¿·¾¿¶¿À XX
67879:i6lji<lB::
YmXDq~s{q~sIqrtqzsI~wtwpw
IX X
ÆÇÈÆÉ/ ÆÊÈÆÉ/ ÆËÈÆÉ/
/ / /
/ / /
X
X
mXÌIÌIrqIÌIuqts{s{qtspsI{}p
IrqIy{zyI~yzqsps
IÌÍÌÎÌI{wwpwI
u
{q{qzsps
IrqI|pwxwpw
wIztw{yzopo
IX
mXÌIrqIÌIÏIpspIzqt{qtspsIqsvstqtq~IIyooIq~tyt{yzopo
IX
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=<>?@A=BCB?D=E;EF?FG==EHI=EH?J<;:HK=:;<H?LMN?O?P?=GF?@:Q=:>:Q<?R:;<H:?SDHFQ<RDH?
T:H:;EUA;BHJ:H?VWO?U:X:?J:Y:;<H:?QEZ<X?[WW8\]^_à8bc8<dE;:U?efge_hfhihaj8kl`_hlakm_h8n[j8nV8
o:?OD?P?HIH?J:Y<d<><H<?<HC:=:R<H<pq?E=U?E=UE?K<p<H<p?o:?QDHGK=E;IHIpI?RD;G>=ERIHIp8rstuv8wY:;?@G?
EJI>JE?<QU:H<=:H?x:H=<F?J:Y:;<HJ:?@<;?<dE;:U?o:;><RD;QE?Q<HRE=?T:H:;EUA;BHJ:H?:=J:?:J<=:H?
Q<HRE=<H?<QU:H<=:H?x:H=<F?J:Y:;<H:?HEQI=?x:U<;<=:@<=:C:Y<H:?F:HJ<H<p?KApB>?x:U<;<H<py?z{;H:Y<H?
@G?A;H:FU:?MO?U:X:?J:Y:;<?|?OD=U?U:X:J:H?U:X:R:?J:Y:;:?QEZ<X?Q<HRE=<?xAQU:;>:FU:J<;y?}EH<?
Q<HRE=?T:H:;EUA;BHJ:H?:Y:;?M?OD=U?J:Y:;<HJ:H?Ep?o:RE?M?OD=U?J:Y:;<HJ:H?SEp=E?@<;?x:H=<F?
J:Y:;<?F<?@G?J:Y:;?D=E?F<?C<ZEpJEH?<QU:H<=:H?M?OD=U?J:Y:;<H:?ERE;=EHE>IRD;?D=QGHq?@G?JG;G>E?
HEQI=?@<;?KApB>?GRxG=E;QIHIp~8
8
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
s7v
8
svD;G=E;IH?KApB>B?<K<H?ZUUXyCDHU;D=D;=JyUF?8:@?@EY=EHUIQIHJEH?w?
ll̀`8h`8e8f`8:H:R?RxG=E>EQI?@A=B>BHB?ae__hh;EF?RE;JI>?E=E@<=<;q?J:H:R?
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567789:6;6<=89>8?8;>@A=B7;CB?DB;BEB9;:@;<B9@;6<98;FBF>@GB9;CH;:@9@<@;6B>;>@A=B7;CB?DB;CI?JGJ9:@9;
KLMLMNLOLPQNQMRQOQSTUU
U
VWXYZ[Z\Z]^Z_B̀B7F@?;:@9@<;A=>6G89:6;ab;c@;ad;DB=BeB9@;6<98;FB9<6?B;fFB9JFg;76=@g;JED@9;c@;hi;
A?G67;J`@=@j;c@=:BkB9B̀:@;FBF>@GB9;E878e8989;96F8?;A?:HkH9H;DI`?@G?@<B9B̀l;m?:8k898̀;
FA9HE?6=8;<A=HG?6<898̀l;U
nopqrstZ
U
VWXYZuZ\Z]^Zh@c=@:@7B;D@=B?BG;CI?JvJ;:B=@9E?@=B;FBGJ?6>I=;A=>6G896;:65B?;@:B?G@GBe>B=l;wbx;a;
yzU{bx;a;DB=Be;C@F?@G@;76<967?6=8;<@=B9@;xag;b|a;c@;bx;a;>@}@;:@k@=B9@;F65B};hig;76=@g;
JED@9;c@;FB9JF;FB9<6??@=B;H<DH?69:8k89:6;ab;c@;ad;HE?6=896;:Je@v@7;D@=B?BG;F@cB<@FB9B;
5@F6}?6<898̀l;~@F6}?6:8k898̀;:@k@=?@=@;DI=@;FBGJ?6>I=;A=>6G89:6;ad;c@;abB9;D=6B7?@=B9B;
EB̀:B=B9B̀l;~@F6}?6G6;Be?@G?@=B9B;6E87?6<898̀lUU
nopqrstZ
U
VWXYZZ\Z]^Zab;HvH96;x;~`;=@769F89:6;d|;a;>@}@;:@k@=B9@;F65B};FB9JF;Be6=@>B;B?@;ad;HvH96;b|;
~`;=@769F89:6;b|;a;>@}@;:@k@=B9@;F65B};76=@;:6?D6;H<DH?6<898̀;c@;E878e8;DI`?@G?@<B9B̀l;
m?:8k898̀;FA9HE?6=8;<A=HG?6<898̀lU
nopqrstZ
U
VWXYZZ\Z]^ZI<?@;CB=UE876=G6;:@c=@FB9:@7B;dd;
;:@k@=B9@;F65B};:B=@9E?@=g;6<98;:@k@=@;F65B};
676>;6=7?8;:@k@=:@;:B=@9E?@=?@;<@=;:@kBe>B=B?B=F@;UE878e8989;96F8?;@>7B?@9@v@kB9B;
@?@7>=A9B7;FBGJ?6F<A9;<6`8?8G?6=8;7H??696=67;6E87?6<898̀l;U
nopqrstZ
U
VWXYZZ\Z]^Z_6=7?8;>J=:@7B;E876=G6;:@c=@?@=B9@;I=9@7?@=;c@=@=@7;5@=UCB=B9B;6E87?6<898̀l;U
nopqrstZ
U
VWXYZZ\Z]^Z5@6>F>A9@;7I}=JFJ;B?@;B?DB?B;I=9@7;CB=;5@F6}?6G6<6;6B>;EI`JG;Be?@G?@=B9B;;
:B=@9vB9B;CH?G67;J`@=@;:Bk@=;:B=@9E;:@k@=?@=B9B;7@9:B9B̀;C@?B=?@<@=@7;DIF>@=B9B̀l;~@F6}?6G6;
FA9HE?6=898̀8;:Bk@=;:B=@9E?@=B9;6<=8;6<=8;:@kBeBGB9@;DI=@;<A=HG?6<898̀l;U
nopqrstZ
U
VWXYZZ\Z]^Z876=G6;:@c=@?@=B9B9;9@=@?@=:@;c@;9@;6G6E?6;7H??698?:8k898;6E87?6<898̀l;
mE87?6G698̀8;I9@=B?@=B9B̀;@e?BkB9:@;D@9Be?@>B9B̀l;U
0112340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:;<
=>?@<A<B<AC<DEFGHIJHFKLMMNOGLFPQRLJMSNFTUJEFKLVNJSLWNONVFXYUJESLJFVUJFOZ[HSZM[HFUS\LSNGNJFIHF
]^V_\_O_FKLVNJSL\LWLF`HJHMFWUM[EJaFYUJESLJFWEMLJNGLMZSHJGHOFRLJMSNFUSLbLM[NJaFDLTZ[FTUJESLJF
GHcHJSHOGZJ\HWHFLSNO\LWLbLM[NJadQ
56789:;<
<
<
0123420
TEORĐK BĐLGĐ
Sayfa 1 / 3
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.6):
Aşağıdaki şekilde bir "Gerilim Đzleyici" görülmektedir.
Bu şekilden de görüldüğü gibi işlemsel yükseltecin çıkışı aynı zamanda eksi girişe bağlanmıştır. Bir
işlemsel yükseltecin çıkış formülü;
e3 = A (e2 - e1) dir. Burada A işlemsel yükseltecin kazancıdır. Gerilim izleyici için aynı formülü
kullanırsak;
e3 = Ao (e2 - e1) = e1 olur. Burada Ao, açık döngü kazancıdır.
Buradan e2 - e1 = e1 / Ao yazılabilir.
e1 in 1V değiştiğini düşünelim. Bu değişiklik giriş uçları arasında 1 / Ao lık bir değişim oluşturur.
Yani;
(e1 + 1) / Ao = e2 - (e1 + 1)
Eğer Ao çok büyükse ya da ideal işlemsel yükselteç deki gibi açık döngü kazancının "sonsuz"
olduğunu düşünürsek, o zaman;
e2 - e1 = e1 / Ao
e2 - e1 = e1 / ¥
e2 - e1 = 0 olur.
Yani giriş uçları arasında bir gerilim farkı olmaz. Yani e2 = e1 olur. e1 = e3 olduğuna göre, e2 ucuna
uygulanan gerilim e3 olarak çıkıştan alınır. Bu devrenin giriş gerilimi çıkış geriline eşit olur. O zaman
devrenin kazancı da "1" olur. (e1 = e2 = e3)
Giriş empedansı;
Giriş empedansını "Z" ile gösterelim. Örneğin çıkış voltajı 1V ise (ya da giriş voltajı 1V ise)
e2 - e1 = e1 / Ao
e2 - 1 = 1 / Ao oluyordu. O zaman;
e2 = (1 / Ao) + 1 olur. Ohm kanununu kullanarak ve biraz da kısaltarak devrenin girişi üzerinden yada
Z üzerinden akan akımı yazarsak;
iZ = (1 / Ao) /Z
iZ = 1/ (Ao x Z) olur.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_06/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 3
Devrenin etken giriş empedansı;
Zet = e2 / iZ
Zet = (1 + 1 / Ao) / (1 / Ao )
Zet = Z (1 + Ao) olur.
Đşlemsel yükselteçlerin kendi iç kazançlarının "open loop gain" çok yüksektir. Yukarıdaki formülden
de anlayacağımız gibi gerilim izleyicinin giriş empedansı yaklaşık olarak işlemsel yükseltecin iç
kazancı "open loop gain" ile iki giriş ucu arasındaki empedansın çarpımı ile bulunur. Pratikte bu çok
yüksek bir değerdir.
Bu devrede olduğu gibi devrenin (işlemsel yükseltecin değil, devrenin tamamının) kazancını biz tayin
ediyorsak bu kazanca kapalı döngü kazancı "closed loop gain" denir.
Gerilim izleyicinin üç özelliği, birim kazanç "unit gain" yani kazancın "1" olması, giriş empedansının
çok çok yüksek olması ve çıkış empedansının da çok düşük olmasıdır. Bu özelliklerinden dolayı
girişlerine bağlanan devreyi hiç yüklemeden çıkışlarında giriş gerilimine eşit ve istenilen düzeyde
akım verilen devreler yapılabilir. Örneğin güç kaynaklarının çıkış devrelerini buna bir örnek olarak
verebiliriz. Bir kullanım alanı olarak da çıkış empedansı yüksek devreleri giriş empedansı düşük
devrelere bağlamak için kullanılır. Buna örnek olarak da her türlü yükselteç için çıkış devreleri ya da
ön yükselteç ile çıkış güç devreleri arasındaki "tampon" yükselteci söyleyebiliriz.
Eşdeğer devresinden görüldüğü gibi Vo = Vi 'dir.
Faz terslemeyen yükselteç birim kazançlı bir opamp devresidir. Yani kazancı 1’dir. Bu devre gerilim
izleyici olarak da bilinir. Bu amaca hizmet eden diğer bir devrede emiter izleyicili transistor
bağlantısıdır. Bu devre çok yüksek bir giriş empedansına ve çok düşük bir çıkış empedansına sahiptir.
Bu özelliğinden dolayı genellikle empedans uygunlaştırıcı olarak kullanılır. Değişik yükleri bu devre
kullanarak sürebiliriz.
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_06/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 3
Ayrıca bu devrede giriş ve çıkış gerilimleri birbirine eşit olduğu için ve giriş empedansı çok yüksek,
çıkış empedansı çok düşük olduğu için çıkış güç kazancının giriş güç kazancına oranı çok yüksektir.
Bu özelliğinden dolayı güç kazancı istenen yerlerde rahatlıkla kullanılır.
Bu devre giriş ile çıkış arasında tam bir yalıtım olduğu için çoğu yerde tampon devresi olarak da
oldukça sık bir şekilde kullanılır.
DEĞERLENDĐRME:
OPAMP’ın evirmeyen giriş ucuna sıra ile DC, sinüsoidal, kare dalga ve üçgen sinyal uygulandığın da
opamp çıkışında girişe uygulanan sinyalin takibi gerçekleştiği gözlenmiştir. Girişe DC sinyal hariç
diğer sinyallerin frekans değerleri değiştirildiğinde belli bir frekans derğerinden sonra osilaskopta
gözlenen sinyalde bozulmalar gerçekleşmiştir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_06/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDEFGHFEIJKLHFEMFNIOPQRSQTIMFGFEIUFVFJEFWCX
67879:8@:B:YZ[Z::
67879:?@8=A=:B:\]^_`_abcd`]e_f_:
67879:ghgijB::
YkXPQRSQlmnIopqrsotonIuqrqvIwxwnyIzmryIq{oIzqn|z}I~yroIy{uyIpoI|uonIzqnty{Iwtuw{ynmmnyI
PQRSQXm~mvmnyIuqrqvoIwtuw{ynynIzqnty{qnIy~qIoq{qqnqIqzy{ysy~IX
kXsIq{otqxqIopro{orqnI~w{{ynm{mvXysyxmnmIronso~X
67879:77hg8g<jB::
XXXPQRSQX
678bb:
wIonotIq{oIq{uq{qIo rq~IpoIytrmnm{mI¡q{uq{orIqqnI¢o¡Iy¡yn{mIzqs|{yzt nIwtuw{ysyzmI
qs~£nmIzwnynI¤¥HFHIzqzosqI¢o¡I¡y{ynmzmnyIw{yvsy~I|oroI¦§¨©©ªªª«¬­¬ª¬®©X
ª¯X°­X±²X¯°­±XX
67879:c³´µ¶B::
wIonotIqqnI¢o¡Iy¡yn{mIzqs|{yzt nIwtuw{ysyzmIqs~£nmIzwnynI¤¥HFHIzqzosqI¢o¡I
¡y{ynmzmnyIw{yvsy~IqqnI¦§¨©©ªªª«¬­¬ª¬®©Xª¯X°­X±²X¯°­±XX
67879:g6jhg<jB::
YkXDo~q{o~qIoprotqI~wrwnwIX
X
kXFpqrsotonIuqrqvoInxoI·¸Iuorq{qsqnqIwtuw{ytmnm}I̧¹ILº»{w~I ynzqt soroIq{oIoqvq~I·¸I
oor{orqIqqnI· Iuorq{qsqnqnIoqvqsqnqIqnxo{otqnqI·¸¼· I {wwnwIu{os{otqnqIpoI
y{mmnmIz nwxwIt rws{ytmnmIX
½kXFpqrsotonIuqrqvoI¡wIo¾yI¾ n~zqt nI¿onoryr|n|I~w{{ynyry~I·ÀIuorq{qsqnqIwtuw{ytmnmX
·À»nqnIooIoorqnqIÁlyIytyr{ytmnm}I¾ro~ynzmnmI¸I»onI¡yv{ytyry~IyrmrmnmINm~mvIy{uyI
vo~{qnqnI¡ w{sytyI¡yv{ymmI¾ro~ynzIoorqnqIozqIoqnqIU|v|~I¾ro~ynz{mIuqrqv{oroIm~mvI
zqnty{qnqnI¡ w{symmnm}It|~zo~I¾ro~ynz{yryIqzoIÃĤGÄ»mnIm~mvIzqnty{qnqnI¡ w{wwnwI
u{os{otqnqI¤{mmnmIz nw{yrmIt rws{ytmnmIX
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=>?@ABCDECFG@=HDI@EJHKHLEA<DB@?<EMN=EI>L>KOEMN=EB>KANKEPFNK@DA?HEQ<F<LE<L@FNG<E<J<DE
RSTUVWXY@EZ[F@=@=@KG@IHF\E]ZEIZFZ=@EI<KK@GENI<?=N?<I<F\^
^
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
:
_7`abc`:def6fghijkl9::
^
6789:;CFZ?@FHDEJmn>=>E<J<DEMGGopqqrrr\sCDGFC?rCF?I\GKqE^rNtEt@[?@DGHAHDI@DEuv;w;E
xyxz{Wy|{^Xyz^RU^}{|{Yy|^~NDNBEBQZ?@=@AH~Etm?>=>D>EKZ??@D@F@KEB@FIH=E@?@t<?<FOEINDNBE
M@KKHDI@E@BFHDGH?HEGNCF<KEt<?Q<E<J<DEINEB<DNE@BDHEA<AGN=<DEtZEINDNBNE@<GEGNCF<KEt<?Q<Etm?>=>DINDE
YXXVX|XRyVyxy|yT^^
^
_
:i::kh:@=oCDEINFN?NF<DEDNFN?NFINEKZ??@DH?IH[HDHE@JHK?@BHDHn\EZ??@DH?=@nA@ED@AH?Et<FE
IZFZ=E<?NEK@FLH?@L@s@[HEM@KKHDI@EBCFZ=I@EtZ?ZDZDZn\E^
:
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6
789:;<;=;>?;@ABCDEFGHBIJCKFGALMNOFIJPBJDJBKOJFQRHCSJDGJTUFGBAVNFPWXWFJDJLAODABFCYDDAOABACZF
[BOJCDJBFPJBJBJCF\JB6XKBKOKFATECDAREOE]WF6
^_`abcd;
6
789:;e;=;>?;fghig6KDJFGALMNOFIJPBJFCYDDAOLAOEOFIKjJBFGALMNOFIJPBJFGHBklmnon6pqkkrosrtr6
u[BJFAPAOGAvFPJFIJ]APAOGAvDABEOEFATECDAREOE]WF6
^_`abcd;
6
789:;w;=;>?;xDJCGBNOKCFSKLHDASRNOFRA]EDELDABEFKDJFfghig6KDJFuJBTJCDJyGKBKDJOFXYFIJPBJOKOF
TADEyLASEOEFz{UF|z{FPJF}~{FGJMJFIJjJBKOJFSA\KMF|~F]FVBJCAOSEOIACKFPJFVABCDEFGKMGJCKFSKOHSUF
CABJUFFPJFHTuJOFuKBKyFKyABJGDJBKFKTKOFu[]DJLDJRKOK]WFDIEjEOE]FSNOYTDABEFRNBYLDAREOE]WF6
^_`abcd;
6
789:;;=;>?;fghigEOFX[RDJFXKBFGALMNOFIJPBJIJFSEOEBDECDABEOEFPJFIJ]APAOGAvDABEOEFATECDAREOE]WF
TECDALAOE]EFVABCDEFGHBIJCKFPJFVABCDEFVBJCAOSDABIACKFuKBKyFKyABJGDJBKOJFIJPBJOKOFPJBIKjKF
JPAXEF
IKCCAGJFADABACFuJOKyDJGKOK]FQNGFKLHDASRNOFNBGALEOIAFVABCDEFVBJCAOSFGJMCKDJBKOJFSKSGJLKOF
JPAXE6AROEFCAXYDFJIKDIKjKFKTKOFXYFGKMFAOADK]KFJDJCGBNOKCFSKLHDASRNOFRA]EDELDABEFJyDKjKOIJF
uJBTJCDJyGKBKOK]WZWF6
^_`abcd;
6
789:;>;=;>?;YFIJPBJF\ACCEOIAF6VABCDEFSNBYF\A]EBDAREOE]FQNBYDABF]NBFOKGJDKCGJFNDLADEIEBFPJF
T[]HLHOHF\A]EBDALARAFuJBJCFRNCGYBWFNBYDABFRYCABEIACKDJBIJOFVABCDEFNDA
ACGEBWFASKGFSNBYDABF
IJjJBDJOIKBLJRJFADEOLARA
ACGEBWZ6
^_`abcd;
;
;
;
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 8
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.7):
Đdeal Türev Devresi
Yukarıdaki şekilde ideal bir elektronik türev alıcı devresi görülmektedir. Ok yönleri o kollarda akan
akım yönlerini belirtmek için gösterilmiştir.
Türev alıcı devresi, genel olarak bir eviren yükselteç özelliğindedir. Fark olarak girişte R1
direnci yerine C kondansatörü bulunmaktadır. Genel bir türev alıcı devresi aşağıdaki şekilde
verilmiştir. Türev alıcı, girişinden uygulanan işaretin türevini alarak çıkışa aktaran bir
devredir.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 8
Devrenin çalışmasını kısaca inceleyelim. Girişte kullanılan kondansatör, ac işaretleri geçiren
fakat dc işaretleri geçirmeden üzerinde bloke eden bir devre elemanıdır. Dolayısı ile dc
işaretler için türev alma söz konusu değildir. Gerçekte dc işaretler için türev alıcı çıkışı
Vo=0’dır. Türev alıcı girişine mutlaka sinüsoydal işaret uygulanması söz konusu değildir.
Frekans barındıran veya genliği zamana bağlı olarak değişen bir işaretin uygulanması
yeterlidir. Yukarıdaki şekilde verilen türev alıcı devrenin çıkış gerilimi;
değerine eşittir. C kondansatörü üzerinden akan i akımının değeri ise;
olduğu bilinmektedir. Dolayısıyla bu değer çıkış gerilimi için yeniden düzenlenirse;
olarak ifade edilir. Bu denklemden de görüldüğü gibi çıkış gerilimi (V0), giriş geriliminin
türevi ile orantılıdır.
Türev alıcı devrenin çıkış denkleminde kullanılan; dVin/dt ifadesi herhangi bir anda giriş
işaretinin eğimini veya değişim hızını belirtmektedir. Bu ifade matematiksel olarak türev
fonksiyonu olarak bilinir. Dolayısı ile içerisinde eğim veya değişim barındıran tüm
işaretlerin türevini almak söz konusudur.
yerine "S" koyarsak;
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 8
olur.
Yukarıdaki şekilde girişteki kondansatör üzerinden akan akım işlemsel yükseltecin giriş direnci çok
yüksek olduğu için olduğu gibi direnç üzerinden de akacaktır. Bunu formül ile yazacak olursak;
buradan çıkış gerilimi "e2" yi yazacak olursak;
olmaktadır.S yerine
konursa;
yazılır. Buda giriş sinyalinin türevini alındığını gösterir.
Aynı devre yüksek geçiren filitre olarak da kullanılır. Bir kondansatörün alternatif akıma gösterdiği
direnç
yada
olarak yazılıyordu. Şimdi devrenin girişine uygulanan sinyalin frekansının
çok yükseldiğini düşünün. O zaman kondansatör hiç direnç göstermeyecek ve devre frekansı yüksek
AC sinyali çok yükseltecektir. Frekans düştükçe kondansatörün gösterdiği direnç çok yükselecek ve
devre düşük frekanslarda yükseltme işi yapmayacaktır.
Yukarıda bahsedilen ideal türev devresi pratik uygulamalarda kullanmaya elverişli değildir. Çünkü C1
kondansatörü, yüksek frekanslı giriş sinyallerinde kısa devre özelliği göstererek, üzerindeki gerilim
düşümü en az seviyede olur ve yükseltecin kazancı artar. Yüksek frekanslı giriş sinyallerinde çıkış
işareti maximum seviyeye ulaşır. Vi giriş sinyalinde gürültü mevcut ise devre gürültünün yüksek
frekans bölümünü olduğu gibi yükseltir. Bu istenmeyen durumu engellemek için Görüldüğü gibi
girişe R1 direnci eklenir. Böylece devre kazancına yüksek frekanslarda Rf / R1 oranı gibi bir sınır
getirilmiştir. Bu durumu aşağıdaki devre üzerinde gözlemlemekteyiz.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 8
Pratik Türev Devresi
Yukarıdaki devre için çıkışın girişe oranını s uzayında yazalım.
Yukarıdaki formülden de görüleceği üzere devrenin pratik uygulama şekli ile devrenin çıkışında
C*R1 zaman sabiti kadar bir süre ile zaman sabiti gecikmeli bir cevap alma şekli gözlemlenecektir.
Aşağıdaki grafiğe dikkat edilirse a seçeneğindeki sinyal giriş sinyali olmak üzere pratikteki türev
devresi ile keskin impuls çıkış darbeleri yerine esnek ve uygulamada kullnılabilecek bir çıkış sinyali
görülecektir.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 8
Pratik uygulamalı türev devresinde kritik frekans (Fc) söz konusudur. Çünkü, C ve R1 elemanları ile
oluşturulmuş bir seri RC devresi bu devresi söz konusu olmaktadır. Bu frekans değeri Xc = R1
eşitliğinden faydalanılarak bulunur.
Buradan da Fc değeri çekilirse,
bulunmuş olunur. Aşağıda kritik frekans ile ilgili bir örnek alıştırma yapılmıştır.
Örnek: 200Hz`e kadar olan sinyallerin türevini alan devreyi tasarlayınız.
Çözüm: Burada integratör devresinin tersine Fc kritik frekansı verilen 200Hz in 10 katı
büyüklükte olması gerekir. Zaten işlem bakımından integratör ile türev tam birbirinin
tersi işlem yapmaktadır. Buna göre;
Fc = 10 * 200Hz = 2KHz
bulunur. Eşitlikte yerine konursa,
dir. Fakat burada C kondansatörünün de seçilmesi
gerekmektedir. C = 0,1mF alıp eşitlikte
yerine koyalım ve eşitlikten R1`i çekelim.
bulunur.
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 8
NOT: Sinüs bir işaretin türevi kosinüs işaret şeklinde olacaktır. Kosinüs bir işaretin türevi ise eksi
sinüs bir işaret şeklinde olacaktır. Ancak, devrede dikkat edilmelidir ki giriş işaretleri OPAMP'ın
eviren giriş ucundan uygulandığı için çıkışta normalde beklenen bir işaretin negatifi çıkacaktır. Türev
devreleri üçgen dalga şekillerini kare dalga şekline çevirirler.
Aşağıdaki örnek giriş işaretleri için çıkış sinyalleri verilmiştir. Giriş ve çıkış işaretleri arasındaki farka
dikkat ediniz.
1. Opamp’ın eviren giriş ucuna sinüsoidal sinyal uygulandığında çıkışta sinyalin 90° ötelendiği
gözlenmiştir. Osilaskopta ki gözlenen grafik aşağıda görülmektedir.
Vin= 1 kare=3V
V0=> 1 kare 3V
2. Opamp’ın Opamp’ın eviren giriş ucuna kare dalga sinyal uygulandığında çıkışta sinyalin
kırılma noktalarında sonsuza gittiği diğer sabit değerlerde ise çıkışın sıfır olduğu gözlenmiştir.
Yapılan bu deneye ait osilaskoptaki grafikler aşağıdaki gibidir.
Vin=> 1Kare = 2V
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 8
3. Opamp’ın Opamp’ın eviren giriş ucuna üçgen dalga sinyal uygulandığında çıkışta sinyalin tepe
noktalarında sonsuza gittiği diğer sabit değerlerde ise çıkışın sabit değer aldığı sonuçta ise kare
dalga oluştuğu gözlenmiştir. Yapılan bu deneye ait osilaskoptaki grafikler aşağıdaki gibidir.
Vin=> 1kare = 1V
V0=> 1Kare = 2mV
DEĞERLENDĐRME
Şekilde görülen devre sabit bir gerilim değeri için ( V1 girişi ) çıkış sinyalini “0” olarak gösterir.
Çünkü bir ifadenin türevinin olabilmesi için fonksiyonel, sürekli azalan ya da artan, veya değişken
terimler içermesi gerekir.
Burada Rf ve Ri eşit kabul edilir ve ifade işlemsel olarak aritmetiğe indirilirse
(LAPLACE dönüşümü ) ;
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 8
Bu ifadede devre değişkenleri yerine konursa T.F. ;
Kazancı meydana gelir dirençler değişken olduğundan paydadaki 100 katsayısı değiştirilebilir.
Yapılan türev alıcı devrede çıkış gerilimi yukarıda belirtildiği gib V0= -C*R*dVin/dt formülüile
hesaplanmaktadır.
DEĞERLENDĐRME:
Opamp’ın besleme gerilimi sinüsoidal dalga ile yapıldığında opamp çıkışından alınan sinyalin 90°
ötelendiği gözlenmiştir. Opamp’ın besleme gerilimi kare dalga sinyal ile yapıldığında sinyalin değeri
ne olursa olsun opamp çıkışında sinyal değeri sıfıra eşittir. Bunun nedeni sabit değerlerin türevi sıfıra
eşit olduğu içindir. Ancak kare dalganın köşelerindeki kırılma noktalarında türev sonsuza gitmektedir.
Opamp’ın besleme gerilimi üçgen sinyal ile yapıldığında ise; üçgenin tepe değeri sabit değer olduğu
için bu noktalarda çıkış değeri sıfır olur. Bunun sonucunda çıkışta elde edilen sinyal şekli kare
dalgaya benzemektedir. Rf direncinin değerinin arttırılmasıyla devre çıkışındaki türev etkisi arttırılmış
olmaktadır.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_07/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567689:;<=<9>?7<@<A9BCDEFGEDHIJKGEDLEMHNOPQRPSHLEFEDHTEUEIDEVBW
5676897?9A9XYZY99
567689>?7<@<9A9[\]^_àbcdc9
567689efeghA99
XiWOPQRPjklHmnopmlHqoporHstsluHVvHnmHwxlyulzu{|pH}~mpolymlHzkpuHomHzol}zWW
WW
}qmlHzoluHsqsulykklHyuHOPQRPWkwkrklyuHqopormHsqsululHzoluolH{}pmnololHuklykklkH
WW
iWVHnmHHymmpmpololH{}pmnHwu{zukzkH}~mpolymwoHm{wozoloH|pmlmwHW
iWVHnmHlolHupwkHymmpmpoHoolHkwkrHorupm{ololHrmwolymHxuzkHmwmlomlHymorowooH
WW
iWOPQRPWomHqmpmwmr{opomlH{}pmnHymnpmzololH{pulzmpHxlwzoxlslsHkwupuomwW
iWFu{mu{owzmHxymoHmoHxulH{}pmnHzoz{mololHRQQWxp{uklyuHul W¡¢W
nmHkwkrklkHq|~mmmomwW
5676896£6fe7£e;hA99
vHuym{H¤¥vH¦§¨F§©HªHuym{Hv«HK¬H­x{ulzoxm{pm©HvHuym{HvH®¯W
°±²±³à´µ¶·a¸a¹µº9̀
»sHymlmHomHoqooH{mxpowHnmHupkl{kkHoqompHoolH¼mH{uulkHzo}uzxlHsqsuuzkH
ow½lkHzslulH¨GEGHzoz{moH¼mHuul{kzkluHsuruwH}~mpmH¾¿ÀÀÁÁÁÂà ÃÁÃ
ÀW
Á¢W
W¡W
¢ WW
567689¹Ä¸Å·a¹³Æ²ÇA99
»sHymlmHoolH¼mH{uulkHzo}uzxlHsqsuuzkHow½lkHzslulH¨GEGHzoz{moH¼mH
uul{kzkluHsuruwHoolH¾¿ÀÀÁÁÁÂà ÃÁÃ
ÀWÁ¢W
W¡W
¢ WW
567689e5hf£e;hA99
XiWCmwoymW
¡WÈÈ ÈWW
W
0123240
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;9<=>?@?A?B=CDADEF=GHDIJ=KILF=MFNDEDB=MFNFAOFAMF=H:=PQ=CFADODRDID=S>CSO?>TITUV=HW=
CFADODRDIDI=MFNDEDRDID=DILFOF>DIDUX=HW;Y=WOMSNSIS=CKUOFROF>DIDU=GZ?[D\DI=\]AF^D=;=YJ=^F=
?OMTNTITU=ZWISLS=>WASRO?>TITUX=8
_78`DADEF=GHDIJ=[S=MFa?=aWbBZD>WI=cFIFA?\KA]I]=BSOO?I?A?B=d8HWO\=\F@F=MFNFADIF=Z?eD@=:=
feUgODB=ZDI]ZV=B?AF=^F=]hCFI=H<=CFADODROFADID=S>CSO?>TITUV=HW=CFADODRDIDI=MFNDEDRDID=
DILFOF>DIDUV=CDADE=^F=hTBTE=ZDI>?OOFADIDI=MFNDEDROFADID=?O\=?O\?=hDUDIDUV=MF^AFIDI=CDADE=ZDI>?ODIDI=
\]AF^DID=?OMTNTIT=CKUOFROF>DIDU=^F=ZWIShO?ATITUT=>WASRO?>TITU8ijklm8nNFA=[S=?MTRM?=DZ\FIDOFI=
CFIODB=MFNFADIMF=[DA=DE?AF\=^FARD>WAZ?=ZDI>?O=cFIFA?\KA]IMFI=FOMF=FMDOFI=ZDI>?ODI=DZ\FIDOFI=
CFIODB=MFNFADIF=I?ZTO=CF\DADOF[DOFLFNDIF=BFIMDIDU=hKU]R=CF\DADIDUX=GoAIFNDI=[S=KAbpqrp8ds8rptp8
MFNFAD=<=HWO\=\F@FMFI=\F@F>F=MFNFAF=Z?eD@=ZDI>?OD=CKZ\FARFB\FMDAX=u?ID=ZDI>?O=cFIFA?\KA]IMFI=
FNFA=:=HWO\=MFNFADIMFI=?U=^F>?=:=HWO\=MFNFADIMFI=a?UO?=[DA=CFIODB=MFNFAD=BD=[S=MFNFA=WO?=BD=
LDe?UM?I=DZ\FIDOFI=:=HWO\=MFNFADIF=?>?AO?I?RT>WA=WOZSIV=[S=MSASR?=I?ZTO=[DA=hKU]R=
S>CSO?AZTITUvJw88
x789<y=9:=>?@?A?B=zX=?MTRT=\FBA?AO?>TITU=^F=ZWIShO?ATITUT=>WASRO?>TITUX8
8
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
{
0123450
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;8<=>?@?ABCDEFG<<
H
@7IG<JKLMNOLPQRSTUVWVRXSXQRYZZ[\]]^^^_`KQZLKN^KLNa_Zb]RH^cdRdOeNOQZPfPQaOQRghJiJR
jkjlmnkomHpklHqrHsmomtkoHuvcQcwRxwyMNOWOfPuRdTNVWVQVRbMNNOQOLObRwOLaPWRONOdXNXLzRacQcwR
YObbPQaOROwLPQZPNPRZcKLXbRdXNyXRXSXQRacRwXQcROwQPRfXfZcWXQRdMRacQcwcROXZRZcKLXbRdXNyXRdTNVWVQacQR
tp{p{|popqk|k{jkok}~HH
H
6<C<<B<JORZVLc
Rac
LcfXRXNcR[LOZXbZcbXRZVLc
Rac
LcfXROLOfPQaObXROLbPROSPbNOwPQPU_R
cfO[NOWONOLRcNXeXQacROSPbNOWOQPUPRycQXNcZXQXU_RH
<
H
6<<<B<TwNcRdXLRac
LcQXQRONSObR
cRwVbfcbRLcbOQfNOLaOQRYOQyXfXQXRycSXLaXeXROSPbNOwPQPU_R
gSPbNOWOQPUPRYcfO[NOWONOLzRLcbOQfRZc[bXfXR
cRLcbOQfRdOQaRycQXNXeXRbO
LOWNOLPQPRaVVQcLcbR
ycQXNcZXQXU_RH
<
H
6<<<B<RaXLcQ`XQXRbPfORac
LcRwO[OLObR
cRRacecLXQXHSKbRdVwVbRfcScLcbRfXfZcWRSPbPPQPR
yTUNcWNcwXQXU_RgNaPePQPURfKQMSNOLPRwKLMWNOwPQPU_RH
<
H
6<<<B<RaXLcQ`XQXRbPfORac
LcRwO[OLObR
cRRacecLXQXRSKbRdVwVbRfcScLcbRfXfZcWRSPbPPQPR
yTUNcWNcwXQXU_RgNaPePQPURfKQMSNOLPRwKLMWNOwPQPU_RH
<
H
6<<<B<rHjkjlmnkoHl{pojm{HojktororHqr|ror}HmHHKLZOWPQaORdMRfXfZcWcROXZR
WKacNXRKNMZMLMQMU_R KacNXQRVSycQzRbOLczRvhR
cRfXQVfRyXLXcR̀c
OdPQPRR
cRRfOdXZRbONWObR
VUcLcROLbNPRhzRR
cRhRfOdXZRbONWObRVUcLcROLbNPRzRR
cRhRfOdXZRbONWObRVUcLcROLbNPRR
acecLNcLXRXSXQRyTUNcWNcwXQXU_RgNaPePQPURfKQMSNOLPRwKLMWNOwPQPU_RH
<
H
6<<<B<MRac
LcRYObbPQaOR¡HOLbNPRfKLMRYOUPLNOwPQPUR¢JKLMNOLRUKLRQXZcNXbZcRKNWONPaPLR
cR
STUVWVQVRYOUPLNOWOwORycLcbRwKbZML_RJKLMNOLRwMbOLPaObXNcLacQROLbNPRKNO`ObZPL_ROfXZRj{r|p{H
acecLNcQaXLWcwcRONPQWOwO`ObZPL_£H
H
H
H
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 6
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.8):
Yukarıdaki şekilde ideal bir elektronik türev alıcı devresi görülmektedir. Ok yönleri o kollarda akan
akım yönlerini belirtmek için gösterilmiştir.
Đntegral alıcı devresi, genel olarak bir eviren yükselteç özelliğindedir. Fark olarak geri besleme
hattında R2 direnci yerine C kondansatörü bulunmaktadır. Genel bir integral alıcı devresi aşağıdaki
şekilde verilmiştir. Đntegral alıcı, girişinden uygulanan işaretin integralini alarak çıkışa aktaran bir
devredir.
Đdeal Đntegral Devresi
Devreye zamanla değişen bir e1 sinyali uygulayalım. Kondansatör üzerindeki gerilim;
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_08/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 6
Şimdi bunlar ne demek. Bir kondansatörün üzerindeki gerilim, kondansatör üzerindeki elektrik
yükünün kondansatör değerine bölünmesi ile bulunur.
Eğer kondansatör üzerinden geçen akım zamanla değişiyorsa yani alternatif akımsa
o zaman
kondansatör üzerindeki yükte zaman göre değişecektir. O zaman kondansatör üzerindeki gerilim.
Yük bir elektron akımı olacağı için;
kondansatör üzerinden geçen AC akımın integralini gösterir. Yani DC ye eş değerini gösterir.
Aslında integral almak bir dalga şeklinin yada matematiksel değişle bir fonksiyonun "alanını" bulmak
oluyor.
Buradaki "S" frekansı gösterir. Fakat bu Hz cinsinden değildir.
yada
Sonuç olarak üzerinden alternatif akım geçen bir kondansatör üzerindeki gerilim;
olarak gösterilir.
Tek başına
yada
bir kondansatörün alternatif akıma gösterdiği dirençtir.
Devredeki direnç üzerinden geçen akım akım işlemsel yükseltecin giriş direncinin çok büyük
olduğundan olduğu gibi kondansatör üzerinden geçecektir. Yani;
Buradan çıkış gerilimi;
yada,
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_08/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 6
olarak yazılır. Görüldüğü gibi, devre giriş geriliminin integralini "tümlerini"
almaktadır. Formülün başındaki "-" işareti işlemsel yükseltecin eviren yükselteç biçiminde
çalıştırılmasından olmaktadır.
Aynı devre Alçak geçiren filitre olarak ta kullanılır. Çok basit olarak açıklayacağım. Şimdi Girişe
uygulanan sinyalin frekansının değiştiğini varsayalım. O zaman devredeki kondansatörün işlevi de
değişecektir. Bir kondansatörün direnci ;
ya da
olarak tanımlandığına göre
burada frekansı yükseltmeye başlarsak kondansatörün direncide azalmaya başlayacaktır. Bunun
sonucu olarak yüksek frekanslarda kondansatör çok az direnç göstereceği için devrenin kazancı "-1"
olacaktır. Tersine frekans düşürüldükçe kondansatörün direnci çok yükselecek ve devrenin kazancı
oldukça büyüyecektir. Bu durumda devre alçak frekansı sinyalleri yükselten, yüksek frekanslı
sinyalleri yükseltmeyen bir devre olacaktır. Burada dikkat edilmesi gereken durum yüksek frekanslı
giriş işaretleri kondansatör elemanının kısa devre gibi davranmasına bağlı olarak devre çıkışını
doyuma sokacaktır. Bu durumdan sakınmak için prtaikte ideal en üstte verilen ideal integral devresi
yerine aşağıda gösterilmiş olan pratik integral devresi tercih edilir. Böylece devrenin kazancı
sınırlandıırlmış ve doyuma girerek kararsınlığa meydan vermesi engellenmiş olunmaktadır.
Pratik Đntegral Devresi
Đntegral alıcı bir devrenin, girişine uygulanan işaretin integaralini alabilmesi için yani devrenin
integratör olarak çalışabilmesi için;
1. fgiriş >= fc = 1 / 2 RfCf olmalıdır. (Girişe uygulanan sinyalin frekansı, fc kritik frekanstan
büyük veya eşit olmalıdır).
2. Devrenin zaman sabitesi (T = R1.Cf) ile girişe uygulanan sinyalin periyodu birbirine eşit veya
yakın bir değerde olmalıdır.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_08/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 6
Eğer, devrede bu şartlardan birisi veya ikisi sağlanmıyorsa devre girişine uygulanan sinyalin
integralini alamaz, tersleyen (faz çeviren, inverting) yükselteç olarak çalışır. Bu haliyle devrenin
kazancı -Rf / R1 olur.
Bir altta yer alan şekildeki gibi Vm pozitif tepe değerleri kare dalganın, R-C devresinden oluşan
integral alıcı devrenin girişine uygulandığını düşünelim. Devrenin zaman sabiti kare dalganın
periyodundan büyük olduğu için kondansatör kare dalganın maximum değerine yarım periyodda şarj
olamayacaktır. Ancak, Vc gibi bir değere ulaşacaktır. Aynı şekilde, kare dalga negatif alternansa
geçtiğinde kondansatör tamamen deşarj olamayıp, -Vc gibi bir değere inecektir. Bu durum böylece
periyodik olarak devam ettikçe çıkıştan üçgen dalga alınacaktır. Kondansatörün şarj olup, deşarj
olması, devrenin zaman sabitesi (lineer) olmaktadır.
* Kare dalganın integrali, üçgen dalgadır.
* Đntegral alıcı devreler uzun zaman sabitesi kullanırlar.
Ancak, burada dikkat edilmesi gereken durum giitşin pozitifliğine karşılık çıkışta negatif işaretin
oluşmasıdır. Çünkü, devrede giriş işareti OPAMP elemanının negatif ucundan uygulanmaktadır.
Uzun zaman sabitesi formülize edilirse;
Đntegral Alıcı Devrenin Giriş-Çıkış Dalga Şekilleri
Aşağıda farklı giriş işaretlerine karşılık bu devre uygulaması sonucunda görülecek çıkış sinyalleri
gösterilmiştir. Giriş ve çıkış arasındaki farka dikkat ediniz.
1. Opamp besleme gerilimi sinüsoidal dalga sinyal ile yapıldığında opamp çıkışında gözlenen
sinyalin girişe göre 90° ileri ötelendiği gözlenmiştir. Bu durum ile ilgili osilaskopta gözlenen
grafikler aşağıdaki gibidir.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_08/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 6
Opamp giriş ve çıkış sinyali
2. Opamp besleme gerilimi kare dalga sinyal ile yapıldığında opamp çıkışında gözlenen sinyalin
üçgen dalgaya benzediği gözlenmiştir. Bu durum ile ilgili osilaskopta gözlenen grafikler
aşağıdaki gibidir.
3. Opamp besleme gerilimi üçgen dalga sinyal ile yapıldığında opamp çıkışında gözlenen sinyalin
sinüsoidal dalgaya benzediği gözlenmiştir. Bu durum ile ilgili osilaskopta gözlenen grafikler
aşağıdaki gibidir.
DEĞERLENDĐRME:
Yapılan integral alıcı devrede çıkış gerilimi V0= -1/R*C*∫Vin formülü ile hesaplanmaktadır.
Opamp’ın besleme gerilimi sinüsoidal dalga ile yapıldığında opamp çıkışından alınan sinyalin 90°
ileri ötelendiği gözlenmiştir. Opamp’ın besleme gerilimi kare dalga sinyal ile yapıldığında opamp
çıkışında üçgen sinyal elde edilmiştir. Opamp’ın besleme gerilimi üçgen sinyal ile yapıldığında ise;
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_08/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 6
opamp çıkışında sinüsoidal sinyal elde edilmiştir. Bunun sonucunda çıkışta elde edilen sinyal şekli
kare dalgaya benzemektedir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_08/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567689:;<=<9>?7<@<A9BCDEFGEDHIJKGEDLEMHNOPQRPSHLEFEDHTEUEIDEVBW
5676897?9A9XYZY99
567689>?7<@<9A9[\]^_`ab9cbded9
567689fgfhiA99
XjWOPQRPklmHnopqnmHrpqpsHtutmvHvwqlHvwqlHxpmyxzH{vqnHonHy|rnmHxpmwv}Htwrt}vm~llm~vH
OPQRPW|l{lslm~v{pHtwrt}vmvmHxpmwv}pmHpmnrqv}pmpmHv}lm~llmlmHpxv}vv{HW
jWVHonH
H~nnq}nqpmpmHpmnrqv}H{vxvwlxlHynqpm~n{pHn{pxpmpHqnmn{HW
jWVHonH
mpmHvq{}lH~nnq}nqpHp|pmH|l{lsHpsvqnpmpmHsn{}pm~nH}vxlHn{}nmp}nmH~npsp{}ppH
WW
jWOPQRPWp}nHrnq|n{}nspqp}nmHpmnrqv}H~noqnxpmpmHqvmxnqHm{xpwmtmtH|l{vqvp}n{W
jWRWWWWWWRQ Q¡Wqvlm~vHvmv}ppmpH
wvvp}n{HonH|l{lslmlHr}n}nwnp}n{W
5676896¢6gf7¢f;iA99
£Hv~nH¤¥£H¦§¨F§zH©Hv~nH£ªHK«HvmxpwnqnzH£Hv~nH£ªHm¬W
­®¯®°±c²³´µc¶c·³¸±9
¹tH~nmnwHp}nHp}rp}pHnqp{HonHvwqlml}lHp}rp}nqHp|pmHºnHvvm}lHxpy}vxwmHtwrt}vvxlH
p{»mlHxtmvmH¨
GEGHxpxnpHºnHv}vmlxlmvHt}vsv{HynqnH¼½¾¿¿ÀÀÀÁÀ¿W
ÀWWÂÃWÂWW
567689·[¶Äµc·°Å¯ÆA99
¹tH~nmnwHp|pmHºnHvvm}lHxpy}vxwmHtwrt}vvxlHp{»mlHxtmvmH¨
GEGHxpxnpHºnH
v}vmlxlmvHt}vsv{Hp|pmH¼½¾¿¿ÀÀÀÁÀ¿WÀWWÂÃWÂWW
567689f5ig¢f;iA99
XjWCn{p}~nWÃWÇÇÇÂWW
W
0123410
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:9;<=>?9@A=B@C<=D<E9;9F=D<E<:G<:D<=?H=IJ=K<:9G9L9@9=MNKMGONP@PQR=?S=K<:9G9L9@9@=
D<E9;9L9@9=9@C<G<N9@9Q=T<=US@MVGO:P@PQP=NS:MLGONP@PQW=7
X6789:9;<=>?9@A=YM=D<ZO=ZS@FU9NS@=[<@<:O\B:]@]=FMGGO@O:OF=^7?SG\=\<_<=D<E<:9@<=UO`9_=H=
abcdefF=U9@]UR=FO:<=T<=]VK<@=?g=K<:9G9LG<:9@9=MNKMGONP@PQR=?S=K<:9G9L9@9@=D<E9;9L9@9=
9@C<G<N9@9QR=K9:9;=T<=VPFP;=U9@NOGG<:9@9@=D<E9;9LG<:9@9=OG\=OG\O=V9Q9@9QR=D<T:<@9@=K9:9;=U9@NOG9@9@=
9@\<K:OG9@9=OGDPEP@P=KBQG<LG<N9@9Q=T<=US@MVGO:P@PQP=NS:MLGONP@PQ7hijkl7mE<:=YM=ODPLDO=
9U\<@9G<@=K<@G9F=D<E<:9@D<=Y9:=9;O:<\=T<:L9NS:UO=U9@NOG=[<@<:O\B:]@D<@=<GD<=<D9G<@=U9@NOG9@=
9U\<@9G<@=K<@G9F=D<E<:9@<=@OUPG=K<\9:9G<Y9G<C<E9@<=F<@D9@9Q=VBQ]L=K<\9:9@9QW=>n:@<E9@=YM=
B:@<F\<=H?=\<_<=D<E<:9=g=?SG\=\<_<D<@=\<_<N<=D<E<:<=UO`9_=U9@NOG9=KBU\<:L<F\<D9:W=oO@9=U9@NOG=
[<@<:O\B:]@D<@=<E<:=H=?SG\=D<E<:9@D<@=OQ=T<NO=H=?SG\=D<E<:9@D<@=ZOQGO=Y9:=K<@G9F=D<E<:9=F9=YM=
D<E<:=SGO=F9=C9̀OQDO@=9U\<@9G<@=H=?SG\=D<E<:9@<=ONO:GO@OLPNS:=SGUM@R=YM=DM:MLO=@OUPG=Y9:=
VBQ]L=MNKMGO:UP@PQpAq77
r67s=D9:<@C9@9@=T<=FS@DO@UO\B:]@]@=D<E<:9@9=D<E9;\9:<:<F=tW=ODPLP=\<F:O:GONP@PQ=T<=
US@MVGO:P@PQP=NS:MLGONP@PQW7
7
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
u
0123410
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:7;<=>?>@ABCDEF;;
G
?6HF;IJKLMNKOPQRSTUVUQWRWPQXYYZ[\\]]]^_JPYKJM]JKM̀^Ya\QG]bcQcNdMNPYOeOP`NPQfgIhIQ
ijiklmjnlGojkGpqGrlnlsjnGtubPbvQwvxLMNVNeOtQcSMUVUPUQaLMMNPNKNaQvNK`OVQNMNcWMWKyQ`bPbvQ
XNaaOP`NQNvKOPYOMOQYbJKWaQcWMxWQWRWPQ̀bQvWPbQNvPOQeWeYbVWPQcLQ̀bPbvbQNWYQYbJKWaQcWMxWQcSMUVUP`bPQ
sozoz{onopj{jzijnj|}GG
G
5~;B;;A;oGjnkl
zoMQ`bKbeWQWMbQZKNYWaYbaWQWPYbxKNMQ`bKbeWQNKNeOP`NaWQNKaOQNROaMNvOPOT^Q
beNZMNVNMNKQbMWdWP`bQNROaMNVNPOTOQxbPWMbYWPWT^QG
;
G
5~;;;A;SvMbQcWKQ̀bKbPWPQNMRNaQbQvUaebaQKbaNPeMNK`NPQXNPxWeWPWQxbRWK`WdWQNROaMNvOPOT^Q
fROaMNVNPOTOQXbeNZMNVNMNKyQKbaNPeQYbZaWeWQbQKbaNPeQcNP`QxbPWMWdWQaNKNVMNKOPOQ`UUPbKbaQ
xbPWMbYWPWT^QG
;
G
5~;;;A;Q̀WKbP_WPWQaOeNQ̀bKbQvNZNKNaQbQQ̀bdbKWPWGRJaQcUvUaQebRbKbaQeWeYbVQROaOOPOQ
xSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^QG
;
G
5~;;;A;Q̀WKbP_WPWQaOeNQ̀bKbQvNZNKNaQbQQ̀bdbKWPWQRJaQcUvUaQebRbKbaQeWeYbVQROaOOPOQ
xSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^QG
;
G
5~;;;A;qGijiklmjnGkzonilzGnijsnqnqGpq{qnq|GlG GJKYNVOP`NQcLQeWeYbVbQNWYQ
VJ`bMWQJMLYLKLPLT^Q¡J`bMWPQURxbPyQaNKbyQugQbQeWPUeQxWKWbQ_bNcOPOQQbQQeNcWYQaNMVNaQ
UTbKbQNKaMOQgyQQbQgQeNcWYQaNMVNaQUTbKbQNKaMOQyQQbQgQeNcWYQaNMVNaQUTbKbQNKaMOQQ
`bdbKMbKWQWRWPQxSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^QG
;
G
5~;;;A;LQ`bKbQXNaaOP`NQ¢GNKaMOQeJKLQXNTOKMNvOPOTQ£IJKLMNKQTJKQPWYbMWaYbQJMVNMÒOKQbQ
RSTUVUPUQXNTOKMNVNvNQxbKbaQvJaYLK^QIJKLMNKQvLaNKÒNaWMbK`bPQNKaMOQJMN_NaYOK^QNeWYQizq{ozG
`bdbKMbP`WKVbvbQNMOPVNvN_NaYOK^¤G
G
G
G
0123410
TEORĐK BĐLGĐ
Sayfa 1 / 6
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.9):
Elektronik devre uygulamalarında her hangi bir devrenin giriş işaret kaynağı genellikle bir
gerilim kaynağı şeklindedir. Eğer, herhangi bir devrede giriş gerilimine bağlı olarak bir çıkış
akımı elde ediliyorsa bu tür sistem ve devrelere gerilim kontrollü akım kaynağı denir. Bu tür
sistem veya devreler “gerilim/akım dönüştürücüsü (Voltage-to-Current Converter)” olarak
da adlandırılmaktadır. Gerilim/Akım dönüştürücü bir devrenin çıkışından elde edilecek
akımın, giriş gerilimiyle orantılı olması istenir. Opamp’la gerçekleştirilmiş tipik bir
Gerilim/akım dönüştürücü devrede görülmektedir.
Verilen bu devreyi önceki bölümlerde evirmeyen yükselteç olarak tanımlamış ve analizini
yapmıştık. Devrenin Gerilim/akım dönüştürücü haline gelmesinin başlıca nedeni RL olarak
tanımlanan yük direnci ve bu direnç üzerinden geçen IL akımıdır.
Devreyi dikkatlice incelediğimizde RL üzerinden geçen IL akımının tamamen Vi giriş
gerilimine bağlı olduğunu görürüz. Devrede IĐ=IL’dir. Buradan IL değerini yazarsak;
IL=Ii=Vi/RL
olduğu görülür.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_09/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 6
Devredeki elemanların değerleri:
Vos=2*R*I(B)-e(B)=2*312*0,02-10=2,48 volt
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_09/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 6
Devreyi dikkatlice incelediğimizde RL üzerinden geçen IL akımının tamamen VĐ giriş gerilimine
bağlı olduğunu görürüz. Devrede IĐ=IL’dir. Buradan IL değerini yazarsak;
olduğu görülür. Formülden görüldüğü gibi IL akımı tamamen giriş gerilimi VĐ değerine bağımlıdır.
Şekil-3.25’de verilen devrede RL yük direncinin herhangi bir ucu toprağa bağlı değildir. Bu durum
uygulamada bazı sorunlara neden olabilir.
Bu devre için A noktasındaki düğüm denklemini yazalım.
düzenlenirsek;
elde edilir. Đdeal bir opamp’ın girişlerindeki gerilim farkının 0V olduğunu biliyoruz. Bu nedenle
evirmeyen girişe uygulanan VL gerilimi, opamp’ın eviren giriş terminalinde de görülür. Buradan;
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_09/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 6
yazılabilir. Bu devrede; R3=R4 ve R1=R2 ise VL gerilimi; VL=Vo/2 olacaktır.
olacaktır. Bu sonuç bize IL akımının VĐ giriş gerilimi ile orantılı ve RL yük direncinden bağımsız
olduğunu belirtir.
Yük direnci ve frekans değişimi devreden geçen IL akımını etkilemez.
Bu devrede giriş gerilimi Vin’i referans kaynağı kullanarak kademe kademe değiştirdiğimizde, her
kademede IL akımının değişimi çizilirse giriş işaretinin 0V değeri için çıkışın 4mA ve girişin 10V
değeri için çıkışın 20mA olarak span sınırıların belirlendiği aşağıdaki şekilde görülen doğrusal bir
transfer eğrisi ile karşılaşırız.
Giriş Gerilim Değerlerine Karşılık Ölçülen Çıkış Akım Değerleri Tablosu
Vin değeri (Volt)
Okunana Iı değeri (mA)
0
3.987
1
5.457
2
7.589
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_09/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 6
3
8.895
4
10.354
5
11.854
6
13.598
7
15.478
8
16.83
9
18.42
10
19.74
Devrede Vin ve Vos olmak üzere iki gerilim girişi bulunmaktadır. Burada Vin’i akıtmak istediğimiz
akımı ayarlamak için kullanırız. Vos ise Vin değerinin en küçük değerinde akıtılacak akımı daha
doğrusu ofset akımını ayarlamamıza yarar. Vos ve Vin gerilimleri opampın evirmeyen ucunda
toplanmaktadır. Bu yüzden bu iki gerilim matematiksel olarak toplanır. Va (eviren uçtaki gerilim) Vin
ile Vos ‘un toplamına eşittir. Va=Vb(evirmeyen uçtaki gerilim) olduğuna göre R direnci üzerine
Vin+Vos düşmektedir. Böylece akım değerini bu direnç belirler. Opamp ın ucuna transistor
bağlanarak yükün sürülme işlemi gerçekleşir.
Devrede R direnci gerilim değişim aralığı ile akım değişim aralığının bölümünün yarısına eşittir.
Başka bir değişle gerilim değişim aralığı ile doğru,akım değişim aralığı ile ters orantılıdır.
Vos gerilimi ise direnç üzerindeki maksimum gerilimin iki katı ile Vin e verilecek maksimum
gerilimin farkına eşittir. Devredeki akım Vin,Vos ve R parametrelerine bağlıdır. Vos ve R devrede
sabit olduğu için Vin in değişimine karşılık Iı’da değişimler görülür. Devredeki yükün değişmesi Iı
akımını etkilemez,Iı akımı yük direncine bağımlı değildir.
Vin deki her değişime karşılık doğru orantılı olarak Iı artış gösterir.
Burada giriş gerilimi 5V değerine ayarlandığında ve yük direnci değiştirildiğinde devreden geçen IL
akımının değişmediği görülür. Yük direncinin 1K gibi bir değerine karşılık çıkış akımı değişmezken,
100K gibi yüksek bir değerine karşılık çıkış akımının değiştiği gözlenir.
Bu mekanizmanın yanında piyasada hazır veya paket olarak ta bu gerilim/akım dönüştürücüleri
bulunabilir, aşağıda buna benzer bir örneğe yer verdik.
Ayrıca buradaki DIGIAC 1750 ünitesi üzerinde yer alan bu elemana ilişkin temel
karakteristikleri aşağıdaki tablodaki gibidir:
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_09/informatio... 18.03.2012
TEORĐK BĐLGĐ
Giriş gerilim aralığı
Sayfa 6 / 6
= 0V ile 1.5V arası
Çıkış akım aralığı
= 0 ile 24mA arası
Transfer oranı
= 16 mA/V
Alttaki şekilde ise bu tür dönüştürücülerin daha kompleks bir yapıda üstteki sistemde nasıl
kullanıldıkları gösterilmiştir.
Gerilim-akım dönüştürücüler çeşitli yerde kullanılmaktadır. Özellikle ölçme ve enstrümantasyon
alanında sıklıkla bu dönüştürücülerden yararlanılmaktadır. Fiber optik iletişim sistemlerinde gerilimakım dönüştürücüsü, giriş devreleriyle ışık kaynağı arasında elektriksel bir arabirim vazifesi görür.
Işık kaynağı, ya ışık yayan bir diyod (LED) ya da enjeksiyon lazer diyodudur (ILD). Bir LED ya da
bir ILD tarafından yayılan ışık miktarı, sürme akımının miktarına eşittir. Gerilim- akım
dönüştürücüsü, bir giriş sinyal gerilimini, ışık kaynağını sürmede kullanılan bir akıma dönüştürür.
Bu deneyde işlemsel yükselteç kullanılarak girişte verilen gerilim çıkıştaki yük üzerinde akım olarak
görülmüştür. Devrede oluşan akım besleme gerilimi, giriş gerilimi ve yük direncine bağımlı olarak
değişir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_09/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
4565789:;<;8=>6;?;@8ABCDEFDCGHIJFDCKDLGMNOPQORGKDEDCGSDTDHCDUAV
4565786>8@8WXYX88
456578=>6;?;8@89Z[\]\^_`abcdefghijhkhlhdmnhopgdqharpcpsdtaudvwjrbdxwyrwgjbz8
456578{|{}~@88
W_VNOPQOVG
GGG
G
GG
GV
_VGGGGGGGGGGGV
_VSG
GG GGG
G GV
¡_VA
GGGG GGG¢GGV
£_VKGGMG¤G
GRGG V
4565785¥5|{6¥{:~@88
¦G
G§¨¦G©ª«Eª¤G¬G
G¦GE­¤G¦G
G¦GJ­G
GMU¤GUR¤G¦®GJ­G
¯°±²³´µ¶°·¸±¹¸Vº»¼½VHIJR¤G¦G
GTªTG
GM¾¿ÀÁ½V¾¿ÀÁýV¾¿ÄŽV¾ÆÄÅÂÇÈV
6>É_W@VÊGGGGGGTªTG
GGË̦®§¤GË̦®Í¤GË̬Χ¤G
¾ÆÄÅÂVϵ¹ÈVV
6>É_@VÊGGGGGGªTªG
GGË̬ÎͤGËS¬ÎÍGGV
456578̀ÐÑÒÓ`Ô`ÕÑÖd8
ËGGGG
GG
GGG×G
GGG
ØGG«ÌFDFG
G×G
GGGÙ±±̄ÚÛÛÜÜÜÈÝ°³±¹°ÞÜ°¹ÞÏȱßÛV
ܸàV²Ï¹¸´µ³µVᵶ²¹¸±V̧ϸàµÞµ¹´µ³µáÈVV
456578ÕtÔâÓ`Õnãäå@88
ËGGG×G
GGGØGG«ÌFDFG
G×G
GGGÙ±±̄ÚÛÛÜÜÜÈÝ°³±¹°ÞÜ°¹ÞÏȱßÛVܸàV²Ï¹¸´µ³µVᵶ²¹¸±V̧ϸàµÞµ¹´µ³µáÈVV
456578{4~|¥{:~@88
W_VBGGGV
0112310
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
67589:9;<=>:9?9@9A9A<BCDB<E<F:FGHAIFJ9<I>K9;9@9A9<LCMB<@N<F:FGH<I>K9;9@><O>P9:@>J<9O9A<
=>:>J?9<Q<P><ERG<I>K>:?>:9A9<S>GFT?FUHAHVW<5
X75QG<I>K>:9A9<P><ERG<I>K>:9A9<9?=9?9<TRYFAG9UR@>Y:>?>:?><S>GFT?FIHKHAHV<I>K>:?>:><FUF:?FUHAHVW<5
Z7589:9;<=>:9?9@9<E9A[9\<:>]>:FAG<JFUAFKH<J^??FAF:FJ<JFI>@><JFI>@><I>K9;Y9:9A9V\<S>:<
JFI>@>I><_`<FJH@HAH<JFUI>I9A9V\<I>K9;a@9A9<O9V9A9VW<B<E<9O9A<L@N\<DB<E<9O9A<bc5de5fghf5
>YY9K9A9V9<=iV?>@?>U9A9V<P><GRA^O?F:HAHVH<]R:@j??>:<>;?9K9AI><UR:^@?FUHAHVW<5
k7589:9;<=>:9?9@9A9<l<E<I>K>:9A><FUF:?FUHAHV\<UjJ<I9:>Am9A9<I>K9;Y9:9A9V\<I>P:>I>A<=>O>A<_`<
FJH@HAHA<I>K9;@>I9K9A9<=iV?>@?>U9A9V<P><GRA^O?F:HAHVH<UR:^@?FUHAHVW5
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
0123410
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
5
6
789:;<96=>?@?ABCDEFG66
5
@8HG6IJKLMNKOPQRSTUVUQWRWPQXYYZ[\\]]]^_JPYKJM]JKM̀^Ya\Q5]bcQcNdMNPYOeOP`NPQfgIhIQ
ijiklmjnl5ojk5pq5rlnlsjn5tubPbvQwvxLMNVNeOtQcSMUVUPUQaLMMNPNKNaQvNK`OVQNMNcWMWKyQ`bPbvQ
XNaaOP`NQNvKOPYOMOQYbJKWaQcWMxWQWRWPQ̀bQvWPbQNvPOQeWeYbVWPQcLQ̀bPbvbQNWYQYbJKWaQcWMxWQcSMUVUP`bPQ
sozoz{onopj{jzijnj|}55
5
7~6C66B6JeQeNcWYQJMVNaQUTbKbQNKaMOQ
eQ`bdbKMbKWP`bQeWeYbVQROaOOP`NaWQ`bdWWVWQ
xSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^Q5
6
5
7~666B6
eQeNcWYQJMVNaQUTbKbQNKaMOQJeQ`bdbKMbKWP`bQeWeYbVQROaOOP`NaWQ`bdWWVWQ
xSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^Q5
6
5
7~666B6LQ`bKbPWPQcWKQbMbaYKJPWaQMNcJKNYLNKQeWVUMNevJPLQvNTOMOVOP`NQbKWMbPQaJLMQ
WRWP`baWQNKaMOQvUaQ`WKbP_WQ`bdbKMbKWQWMbQbKWMbPQaJLMLPQ`OOP`NaWQNKaMOQvUaQ`WKbP_WQ`bdbKMbKWQ
WRWPQROaOOP`NaWQ̀bdWWVWQxSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^Q5
6
5
7~666B6SvMbQcWKQ`bKb`bQVNaeWVLVQxWKWQxbKWMWVQNKNMOdOQWMbQVNaeWVLVQROaOQNaOVQ
NKNMOdOPOPQPbQJM̀LdLPLQcLMLPLT^QfROaMNVNPOTOQXbeNZMNVNMNKQbMWdWP`bQbQeOPOKMNKOPQebcbcWPWQ
NROaMNvNKNaQxbPWMbYWPWT^Q5
6
0123410
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
6789:;:<:=>:?@ABCDECFGCGHIJKLDJMNE@COPFQJE@CRSJPETJDUEECFHECFJVTIPOEPJKLDWTEOTVJRTXBTETBPFTJ
YBFTDETBJXTBPFPZ[J5
\]^_`ab:
5
6789:=:<:=>:cUJRTXBTJdCDDHFRCJe5NCBDEHJW@BUJdCZHBECKHFHZJMf@BUECBJZ@BJFPOTEPDOTJ@EGCEHRHBJXTJ
VYZLGLFLJdCZHBECGCKCJQTBTDJK@DOUB[Jf@BUECBJKUDCBHRCDPETBRTFJNCBDEHJ@ECgCDOHB[JcCWPOJW@BUECBJ
RThTBETFRPBGTKTJCEHFGCKCgCDOHB[S5
\]^_`ab:
5
5
5
0123410
TEORĐK BĐLGĐ
Sayfa 1 / 4
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-1.10):
Elektronik devre uygulamalarında her hangi bir devrenin giriş işaret kaynağı genellikle bir
gerilim kaynağı şeklindedir. Eğer, herhangi bir devrede giriş gerilimine bağlı olarak bir çıkış
akımı elde ediliyorsa bu tür sistem ve devrelere gerilim kontrollü akım kaynağı denir. Bu tür
sistem veya devreler “gerilim/akım dönüştürücüsü (Voltage-to-Current Converter)” olarak
da adlandırılmaktadır. Gerilim/Akım dönüştürücü bir devrenin çıkışından elde edilecek
akımın, giriş gerilimiyle orantılı olması istenir. Opamp’la gerçekleştirilmiş tipik bir
Gerilim/akım dönüştürücü devrede görülmektedir.
Verilen bu devreyi önceki bölümlerde evirmeyen yükselteç olarak tanımlamış ve analizini
yapmıştık. Devrenin Gerilim/akım dönüştürücü haline gelmesinin başlıca nedeni RL olarak
tanımlanan yük direnci ve bu direnç üzerinden geçen IL akımıdır.
Devreyi dikkatlice incelediğimizde RL üzerinden geçen IL akımının tamamen Vi giriş
gerilimine bağlı olduğunu görürüz. Devrede IĐ=IL’dir. Buradan IL değerini yazarsak;
IL=Ii=Vi/RL
olduğu görülür.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_10/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 4
Devredeki elemanların değerleri:
Vos=2*R*I(B)-e(B)=2*312*0,02-10=2,48 volt
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_10/informatio... 18.03.2012
TEORĐK BĐLGĐ
IL
Vin
4 mA
0 volt
4,5 mA
2 volt
8 mA
3 volt
13 mA
5 volt
15 mA
7 volt
18 mA
8 volt
20 mA
10 volt
Sayfa 3 / 4
Vin-IL grafiği çizilirse aşağıdakine benzer doğrusal bir grafik ile karşılaşılacaktır.
Yük direnci ve frekans değişimi devreden geçen IL akımını etkilemez.
Yukarıdaki devreyi daha sade ve anlaşılır bir şekilde incelemek istersek aşağıdaki devreyi elde
edebiliriz.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_10/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 4
Bu devrede akımların yönü daha net bir şekilde görülmektedir,
Bu devre için A noktasındaki düğüm denklemini yazacak olursak,
denklemini elde ederiz. Bu denklemi düzenlersek de,
şeklinde olur.
Đdeal bir opamp’ın girişlerindeki gerilim farkının 0V olduğunu biliyoruz. Bu nedenle
evirmeyen girişe uygulanan VL gerilimi, opamp’ın eviren giriş terminalinde de
görülür. Buradan;
yazılabilir. Bu devrede; R3=R4 ve R1=R2 ise VL gerilimi; VL=Vo/2 olacaktır. Bu değer denklem3.1’de yerine konulursa;
olacaktır. Bu sonuç bize IL akımının VĐ giriş gerilimi ile orantılı ve RL yük direncinden bağımsız
olduğunu belirtir.
Devrenin basitleştirilmiş haline ait şeklin a bölümünde verilen gerilim/akım dönüştürücü devreyi daha
basit hale getirmek için devrede kullanılan dirençleri R1=R2=R3=R4=R şeklinde seçebiliriz. Bu
durumda devremiz şimdi b bölümünde verilen şekle dönüşür. Bu ise bize analiz kolaylığı sağlar.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_01_10/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
4565789:;<;8=>6;?;@8ABCDEFDCGHIJFDCKDLGMNOPQORGKDEDCGSDTDHCDUAV
4565786>8@8WXWYX88
456578=>6;?;8@89Z[\]\^_`abcdefghijhkhlhdmnopkqarqgcbidshartctudntadvqjrbd
wqxrqgjby8
456578z{z|}@88
W_VNOPQOV~G
G~
G
~~G
G
G
~~G
~GV
_V
~G
~G~
~~GGGGG
~~G
GG~~~G~~V
_VS
~G~
~G
G
~G~~GG~~~G
GV
¡_VA~G~
~GGG
G~~G
~G¢
G~GV
£_VLGG
G
~~G~~~G
~GV
¤_VK
GGM
GRG
G
V
4565785¥5{z6¥z:}@88
¦V§¨©ªV«¬¦VNOPQO­V¬V§¨©ªV¦®®VJ¯°GGG±GJ¯G~
GMUR°G²GGGJ¯G
~
GMUGGUR°GGJ¯G~
GM³´°GHIJR°GGGTµTG
~
G
¶·¸¦®«­V·¸¦®¹­V·¸º»«­V·¼º»«½¾V
e¿À¿Ád̀ÂÃÄÅ`Æ`ÇÃÈd8
ÉGG~G~~~G
~GG
G~~
G~~GÊGG~GG
~ËGGÌÍFDFG~~GÊG GG
GΪªÏÐÑÑÒÒÒ¾ÓÔÕªÖÔ×ÒÔÖר¾ªØÑV
Ò©ÙV§¨Ö©ÚÛÕÛVÜÛݧ֩ªV©¨©ÙÛ×ÛÖÚÛÕÛܾVV
456578ÇÞÆßÅ`ÇÁàÀá@88
ÉGG~~GÊGG~GG~ËGGÌÍFDFG~~GÊG
GG~~GΪªÏÐÑÑÒÒÒ¾ÓÔÕªÖÔ×ÒÔÖר¾ªØÑVÒ©ÙV§¨Ö©ÚÛÕÛVÜÛݧ֩ªV©¨©ÙÛ×ÛÖÚÛÕÛܾVV
456578z4}{¥z:}@88
W_VB~ØÛV̈©âÖ©ÝÛVØãÖãÕãܾVV
0123210
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
67589:9;<=>:9?9@9A9A<BCDB<E<F:FGHAIFJ9<I>K9;9@9A9<LCMB<@N<F:FGH<I>K9;9@><O>P9:@>J<9O9A<
=>:>J?9<Q<P><ERG<I>K>:?>:9A9<S>GFT?FUHAHVW<5
X75QG<I>K>:9A9<P><ERG<I>K>:9A9<9?=9?9<TRYFAG9UR@>Y:>?>:?><S>GFT?FIHKHAHV<I>K>:?>:><FUF:?FUHAHVW<5
Z75[\:9;<=>:9?9@9<E9A]9^<:>_>:FAG<JFUAFKH<J`??FAF:FJ<JFI>@><JFI>@><I>K9;Y9:9A9V^<S>:<
JFI>@>I><ab<FJH@HAH<JFUI>I9A9V^<I>K9;\@9A9<O9V9A9VW<B<E<9O9A<L@N^<DB<E<9O9A<MB<@N<>?I><
>YY9K9A9V9<=cV?>@?>U9A9V<P><GRA`O?F:HAHVH<_R:@d??>:<>;?9K9AI><UR:`@?FUHAHVW<5
e7589:9;<=>:9?9@9A9<f<E<I>K>:9A><FUF:?FUHAHV^<UdJ<I9:>Ag9A9<I>K9;Y9:9A9V^<I>P:>I>A<=>O>A<ab<
FJH@HAHA<I>K9;@>I9K9A9<=cV?>@?>U9A9V<P><GRA`O?F:HAHVH<UR:`@?FUHAHVW5
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
0123410
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
5
6
789:;<96=>?@?ABCDCEFG66
5
@8HG6IJKLMNKOPQRSTUVUQWRWPQXYYZ[\\]]]^_JPYKJM]JKM̀^Ya\Q5]bcQcNdMNPYOeOP`NPQfgIhIQ
ijiklmjnl5ojk5pq5rlnlsjn5tubPbvQwvxLMNVNeOtQcSMUVUPUQaLMMNPNKNaQvNK`OVQNMNcWMWKyQ`bPbvQ
XNaaOP`NQNvKOPYOMOQYbJKWaQcWMxWQWRWPQ̀bQvWPbQNvPOQeWeYbVWPQcLQ̀bPbvbQNWYQYbJKWaQcWMxWQcSMUVUPrln5
sozoz{onopj{jzijnj|}55
5
7~6C66B6JeQeNcWYQJMVNaQUTbKbQNKaMOQ
eQ`bdbKMbKWP`bQeWeYbVQROaOOP`NaWQ`bdWWVWQ
xSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^Q5
6
5
7~666B6
eQeNcWYQJMVNaQUTbKbQNKaMOQJeQ`bdbKMbKWP`bQeWeYbVQROaOOP`NaWQ`bdWWVWQ
xSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^Q5
6
5
7~666B6LQ`bKbPWPQcWKQbMbaYKJPWaQMNcJKNYLNKQeWVUMNevJPLQvNTOMOVOP`NQbKWMbPQaJLMQ
WRWP`baWQNKaMOQvUaQ`WKbP_WQ`bdbKMbKWQWMbQbKWMbPQaJLMLPQ`OOP`NaWQNKaMOQvUaQ`WKbP_WQ`bdbKMbKWQ
WRWPQROaOOP`NaWQ̀bdWWVWQxSTMbVMbvWPWT^QfM̀OdOPOTQeJPLRMNKOQvJKLVMNvOPOT^Q5
6
5
7~666B6SvMbQcWKQ`bKb`bQVNaeWVLVQxWKWQxbKWMWVQNKNMOdOQWMbQVNaeWVLVQROaOQNaOVQ
NKNMOdOPOPQPbQJM̀LdLPLQcLMLPLT^QfROaMNVNPOTOQXbeNZMNVNMNKQbMWdWP`bQbQeOPOKMNKOPQebcbcWPWQ
NROaMNvNKNaQxbPWMbYWPWT^Q5
6
5
0123410
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;:<:=>:?@ABCDECFGHIJKLDJMNB@OFPQPJE@CPRJSEQJDOEECFHECFJTQISUESJKLDVQEUQTJPQWBQEQBSFQJ
XBFQDEQBJWQBSFSYZJ[
\]^_`ab:
[
6789:=:<:=>:cOJPQWBQJdCDDHFPCJe[fCBDEHJV@BOJdCYHBECKHFHYJMg@BOECBJY@BJFSUQESDUQJ@EGCEHPHBJWQJ
TXYLGLFLJdCYHBECGCKCJNQBQDJK@DUOBZJg@BOECBJKODCBHPCDSEQBPQFJfCBDEHJ@EChCDUHBZJcCVSUJV@Bijkl[
PQmQBEQFPSBGQKQJCEHFGCKChCDUHBZR[
\]^_`ab:
[
[
[
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 11
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-2.2):
Bir elektrik devresinin zaman domeninde incelenmesi için, önce o devrenin ya entegre-diferansiyel
denklemlerinin, ya da durum denklemlerinin yazılması gerekir. Bu denklemlerin çözülmesiyle
devrenin zaman domenindeki incelenmesi tamamlanır. Bilindiği gibi, diferansiyel denklemlerin
çözülmesiyle ortaya çıkan çözümü iki parçaya ayırmak mümkündür: Çözümün birinci parçasını
devredeki ilk koşullar, ikinci parçasını da devredeki kaynaklar belirler. Çözümün bu parçalarına,
sırasıyla Öz ve Zorlanmış Çözüm adları verilir. Asimptotik kararlı, diğer bir deyişle t →∞ için durum
geçiş matrisinin sıfıra uzandığı bir devrede, t→∞ giderken öz çözüm sıfıra, zorlanmış çözüm de özel
çözüme ulaşır. Daha açık bir deyişle, asimptotik kararlı bir devrede, devrenin incelenmesine
başlanılmasından belirli bir zaman sonra, tam çözüm büyük bir yaklaşıklıkla özel çözüme eşit olur.
Asimptotik kararlı bir devre için tam çözümü, geçici çözüm ve kalıcı (sürekli) çözüm olarak iki
parçadan oluşuyor diye düşünebiliriz. Asimptotik kararlı bir devre için diferansiyel denklem
sisteminin homojen çözümüne geçici, özel çözümüne de kalıcı çözüm denilmektedir. Geçici çözüm,
başlangıçta çok büyük olsa bile, devre çalışmaya başladıktan belirli bir zaman sonra küçülür, sıfıra
yaklaşır. Kalıcı çözüm, devrede kaynaklar olduğu sürece devam edecek çözümdür. Etkisi çok kısa
sürmesine karşın geçici çözüm bir devrede elemanların seçilmesi bakımından önemlidir. Örneğin,
elektrik enerjisi dağıtım sisteminde (şebekede) sistem çalışırken birdenbire meydana gelen arızadan
(kısa devre gibi) dolayı, arızanın olduğu andan itibaren ortaya çıkan geçici çözümün şebekedeki
hatların, cihazların, ölçü transformatörlerinin ve anahtarların seçimi bakımından bilinmesi gerekir.
Eskiden şebekedeki anahtarların “açma zamanlarının” büyük olmasından dolayı, arıza halinde ortaya
çıkan geçici çözümle açma zamanından kısa sürdüğü için ilgilenilmezdi. Bugün açma zamanları
küçük olduğu için geçici çözümle ilgilenilmesi, şebekedeki elemanların seçilmesinde göz önüne
alınması gerekmektedir. Devrelerin zaman domeninde incelenmesi, birçok cihazın çalışma ilkelerinin
ve işlevlerinin anlaşılması bakımından çok önemlidir.
Zaman sabiti elemanı diferansiyel denklemi birinci dereceden olan bir sistemi temsil eder.
Zaman sabiti elemanın transfer fonksiyonun genel yapısı
şeklindedir. Burada T zaman sabiti olup zaman boyutundadır.
Zaman sabiti elemanı tipinde çalışan kapalı-döngü sistemin blok şeması Şekil 5.1a'da verildiği gibi
olur. Sistemin indirgenmiş blok Şekil 5.l b'de verilmiştir.
Fiziksel yapısı ne olursa olsun, zaman sabiti tipinde transfer fonksiyonuna sahip sistemler aynı giriş
karşısında aynı dinamik davranışları gösterirler. Verilen herhangi bir fiziksel sistem için matematiksel
cevap elde edildikten sonra sistemin fiziksel yapısına göre yorum yapılır.
Zaman Sabiti Elemanın Birim Basamak Giriş Cevabı
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 11
r(t)=u(t) birim basamak fonksiyonun Laplace dönüşümü R(s)=l/s olduğuna göre, aşağıdaki
denklemden cevap fonksiyonu
elde edilir. Yukarıdaki denklemi basit kesirlere ayırıp sabitlerini değerlendirerek;
elde edilir. Zaman alanı cevap fonksiyonu c(t) bulmak için terim terim ters Laplace dönüşümünü
alırsak,
elde edilir. Yukarıdaki denkleme göre cevap t=0 başlangıç değerinde sıfır ve
, nihai değerinde
birim değere eşittir. c(t) üstel fonksiyonunda
den
kadar t'ye değerler vererek karşılık
gelen c(t) değerleri çizilirse aşağıdaki cevap eğrisi elde edilir.
Buna c(t) denkleminde t=T koyarak
şeklinde elde edebiliriz.
Bir sistemin zaman sabiti ne kadar küçükse, cevabı o kadar hızlıdır. Üstel cevap eğrisinin diğer
önemli bir özelliği ise t = 0 daki eğiminin l/T eşit olmasıdır. Bunu şu şekilde gösterebiliriz;
Bu ise; eğer sistemin cevabı başlangıçtaki hızını koruyabilseydi t=T de nihai değerine ulaşabildi
anlamına gelir. Aşağıdaki şekilde verilen üstel cevap
Birinci dereceden sistemin cevap eğrisi
eğrisinde c(t) değer t-T de nihai değerinin %63,22'sine ulaşmıştır, Zaman sabitinin iki katı değerinde
(t=2T) cevap eğrisi nihai değerinin % 86,5 ve bunu izleyen t=3T, 4T ve 5T değerlerinde ise sırasıyla
nihai değerinin % 95, %98,2 ve %99,3 değerlerine ulaşır. Matematiksel olarak cevap eğrisi kalıcı-
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 11
durum haline sonsuz zaman aralığı sonunda erişir. Uygulamada ise cevap eğrisi nihai değerin % 98
ulaştığında veya zaman sabitinin dört katı bir zaman sonra yaklaşık olarak nihai değerine ulaşmış
sayılır.
Sistemin kalıcı-durum halinde hata verip vermediğini bulmak için e(t)=r(t)-c(t) den; birim basamak
için r(t)=l ve
olduğundan,
zaman alanı hata fonksiyonu tespit edilir.
Daha sonra
da
değeri bulunduğundan sistemin basamak giriş karşısında herhangi bir
kalıcı-durum hatası vermediği gösterilmiş olur. Bu durum ayrıca yukarıdaki şekildeki eğriden de
görülebilir.
Zaman Sabiti Sistemlerin Birim Rampa Giriş Cevabı
Birim rampa fonksiyonun Laplace dönüşümü
rampa giriş cevap fonksiyonu
olduğuna göre zaman sabiti sistemin
olur. Kısmı kesirlere ayırırsak;
elde edilir ve terim terim ters Laplace dönüşümünü alarak zaman alanı cevap fonksiyonunu aşağıdaki
şekilde elde ederiz.
Yukarıdaki denklemde
den
kadar değerler vererek karşılık gelen cevap eğrisini c(t)
aşağıdaki şekildeki gibi elde ederiz. Sistemin hata sinyali e(t) ise,
Zaman sonsuza giderek meydana gelen kalıcı-durum hatası;
olarak sabit bir kalıcı-durum hatası meydana gelir. Aşağıdaki şekilden de
Şekil 5.3 Birinci dereceden sistemin birim rampa cevabı
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 11
görüldüğü gibi meydana gelen kalıcı-durum hatası T ye eşit olur. Bu durumda sistemin zaman sabiti
ne kadar küçük ise meydana gelebilecek kalıcı-durum hatası da o oranda küçük olur.
Zaman Sabiti Sistemlerin Birim Anidarbe Giriş Cevabı
Birim anidarbe fonksiyonu Laplace dönüşümü R(s)=l olduğuna göre birinci derece sistemin cevap
fonksiyonu
olur. Ters Laplace dönüşümü alınırsa
Şekil 5.4 Birinci dereceden sistemin birim anidarbe cevabı
elde edilir,
denkleminde
den
kadar değerler verirsek
Yukarıdaki şekilde görülen cevap eğrisi elde edilir.
Sistem bir anidarbe giriş uyarısı karşısında sabit değerden başlayarak, kararlı ise zaman sonsuza
giderken üstel olarak başlangıç durumuna geri döner.
Zaman sabiti elemanının indirgenmiş blok diyagramı şu şekilde elde edilir.
Vi(s)=VR (s) + VC(s)
VR(s)=Vi (s) – VC(s)
VC(s)= VO(s)
VR(s)=Vi (s) – VO(s)
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 11
En genel halde cevap;
c(t) = 1 – e-αt
t = 1 aolması durumunda e−at = 1 e = 0.37 olur.
c(t) = 1− 0.37 = 0.63
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 11
Burada 1 azaman sabiti (sn), a üstel frekans (Hz)’dir. Zaman sabiti basamak cevabının son değerinin
%63’üne yükselinceye kadar geçen süreye eşittir. Sistemin kutbunun s düzlemindeki yeri aynı
zamanda üstel fonksiyonun üssünü verir.
Yükselme Zamanı (Tr):
Basamak cevabının son değerinin %10’undan %90’ına ulaşıncaya kadar geçen süredir.
1 – e-at = 0.9 ve 1 – e-at = 0.1 işlemlerinin farkı alındığında Tr bulunur.
Yerleşme Zamanı (Ts):
Basamak cevabının kendi son değerinin %98’ine ulaşıp orada kalıncaya kadar geçen
süredir.
1 – e-at = 0.98
Birinci Dereceli Transfer Fonksiyonunun Deneyle Elde Edilmesi:
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 11
Şekilden cevabın 0.72 değerine oturduğu görülmektedir.
0.72×0.63=0,454
Zaman sabiti elemanının , birim basamak girişe cevabının başlangıç anında sıfır olduğu τ kadar
zaman sonra , erişeceği son değerin % 63.2’ sine vardığı , 4τ kadar zaman sonra % 2’ den daha
küçük bir hata ile son değere eriştiği görülmektedir. Ölçme elemanının zaman sabiti τ ne kadar
küçükse sistemin cevabı o kadar hızlı olacak , son değere ulaşma ve gerçek değeri gösterme zamanı o
kadar azalacaktır.
r(t) = u(t) birim basamak fonksiyonun laplace dönüşümü R(s) = 1/s olduğuna denklemden cevap
fonksiyonu
1
Ts+1
1
C(s) =
s
elde edilir. . Zaman alanı cevap fonksiyonu c(t) bulmak için terim ters laplace dönüşümü alırsak,
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 11
c(t) = 1-e-t/T elde edilir. Denkleme göre cevap t = 0 başlangıç değerinde sıfır ve t = ∞ , değerinde
birim değere eşittir. Bu tür üstel bir eğrinin en önemli karakteristiği ise t = T de c(t) nın 0,632 eşit
olması veya diğer bir deyişle c(t), cevabının ulaşması gerektiği değerinin %63,2 ye ulaşmış olmasıdır.
Buna c(t) denkleminde t = T koyarak aşağıdaki şekilde elde edebiliriz.
c(t) = 1-e-1 = 0,632
Burada T zaman sabiti olup birinci dereceden sistemlerin dinamik davranışı ile ilgili temel bir
parametresidir. Buna göre bir sistemin zaman sabiti ne kadar küçükse, cevabı o kadar hızlıdır. Üstel
cevap eğrisinin diğer önemli bir özelliği ise t = 0 daki eğiminin 1/T eşit olmasıdır. Bunu şu şekilde
gösterebiliriz;
de
1
dt
T
1
=
e-t/T t = 0 =
T
Bu ise; sistemin cevabı başlangıcındaki hızını koruyabilseydi t = T da gerçek değerine ulaşabilirdi,
anlamına gelir. c(t) değer t = T de gerçek değerinin %63,2 sine ulaşmıştır. Zaman sabitinin iki katı
değerinde (t = 2T) cevap eğrisi gerçek değerinin %86,5 ve bunu izleyen t = 3T,4T ve 5T değerlerinde
ise sırasıyla gerçek değerinin %95, 98,2 ve 99,3 değerlerine ulaşır. Matematiksel olarak cevap eğrisi
kalıcı durum haline sonsuz zaman aralığı sonunda erişir. Uygulamada ise cevap eğrisi nihai değerin %
98 ulaştığında veya zaman sabitinin dört katı bir zaman sonra yaklaşık olarak gerçek değerine ulaşmış
sayılır. Sistemin kalıcı durum halinde hata verip vermediğini bulmak için e(t) = r(t) – c(t)den; birim
basamak için r(t) = 1 ve c(t) = 1 – e-t/T olduğundan e(t) = e-t/T zaman alanı hata fonksiyonu tespit
edilir. Daha sonra t
∞ da e(∞) = 0 değeri bulunduğundan sistemin basamak giriş karşısında
herhangi bir kalıcı durum hatası vermediği gösterilmiş olur.
Zaman sabitini 1/RC formülü ile hesapladığımızda
0.001 değerini elde ediyoruz. Deneyimizde bu
değeri 0.00124 olarak ölçtük.
Zaman sabitinin 2 ms olması için Zaman
sabiti=R*C den R=2/10-8 ile direnç değeri
=200Mohm olarak bulunur. Bu değişim sonrası
(R’in yeni değerinden sonra) referans çıkışın
referans değerinin %63’üne ulaşması için (0.002 s)
2 ms’lik bir zamana gerek vardır.
Matlap aracılığı ile bu sistemi oluşturduğumuzda 1V değerindeki basamak girişe karşı
aşağıdaki çıkışı elde ederiz.
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 9 / 11
Bu
sistemin
transfer
fonksiyonu
ise
olarak bulunur.
9
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 10 / 11
Zaman Sabiti elemanın step’e cevabı
Sistemin zaman sabiti
dir. Bu durumda olur. Vin=1V kare
dalga uygulandı ve aşağıda görülen çıkış alındı. Vo ın 0.63 V değerine ulaşması için geçen süre
osilaskopun kursör özelliği kullanılarak 1.16 ms olarak ölçüldü. Buradan Vo ın 0.63 V değerine
ulaşması için 1.16 τ lık zaman geçmesi gerektiği anlaşılıyor.
Sistemin zaman sabitini 2ms yapmak için R=200kΩ yapıldı.
dir. Vin=1V kare dalga uygulandı ve aşağıda görülen çıkış alındı.
Vo ın 0.63 V değerine ulaşması için geçen süre osilaskopun kursör özelliği kullanılarak 2.32 ms
olarak ölçüldü. Buradan Vo ın 0.63 V değerine ulaşması için yine1.16 τ lık zaman geçmesi gerektiği
anlaşılıyor.
10
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 11 / 11
Yukarıdaki şekillerde çıkış vevabındaki üstteki doyum RC sisteminin giriş işaretinin frekansının çok
büyük olmasına ve buna cevap vermede yavaş davranmasından dolayı kaynaklanmaktadır. Eğer giriş
işareti frekansı düşürülürse cevabında belli bir değere oturduğu rahatlıkla görülebilir.
MATLAB ile RC sistemi modellenmek ve basamak cevabı görülmek istenirse aşağıdaki komutlar
icra edilecektir.
>> R=100*10^3;
C=10*10^-9;
pay=1;
payda=[1/(R*C) 1];
>>
>> S=tf(pay,payda)
>> step(S)
>> grid
DEĞERLENDĐRME:
ile verilen transfer fonksiyonuna sahip olan devreye birim basamak
uygulandığında
cevabı alınacaktır. Burada τ = R.C değeri ∞ değerini alınca
olacaktır. Burada C(t) = Vo olarak alınmıştır. Yani sistemin genliği birim basamak için
daima 1 dir. R nin değişimi Vo ın dalga şeklini geçici rejimin süresi açısından değiştirir. Geçici
rejimin süresi τ cinsinden değişmez.
R değerini (enerji harcayan elemanın değerini) arttırınca sistem daha geç cevap vermeye başlar. Bu
durumda zaman sabiti artacaktır. Daha önce referans değerinin %63’üne 1 ms değerinde ulaşırken, bu
sefer bu süre 2 ms olmuştur. Burada zaman sabitine hangi (R C) parametrelerin etki etiğini ve zaman
sabitinin sistem üzerinde nasıl bir etki ettiği gözlemlenmiştir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
11
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=<>?:>@AB:CD<>B:E<F>=:?GHI8
JKLKM8NOPQP8RSLPTPU8VWXYZY[\W[]^_W`aY[_WbYc[ZW\defg
JKLKM8LS8U867h788
JKLKM8RSLPTP8U8ijklmn>:opqkln>rstslupvs>@swmpqsl>=pxkyn8
JKLKM8z{z|}U88
h~g[
[
[
[Z[dZ[
[`
[[
[[
[
[[
g
6~g[
[
[
[[
[ [
[[g
¡~g[
[[
[
[
[[¢£[¤[[£
g
¥~g[
[
[[
[¢
[¢¤[¤£
g
¦~g§¨©ª¨«g[
[
[
[£[¤[
g
JKLKM8K¬K{zL¬zO}U88
­[
[­®[`¯[¤
g­[
[°±[`¯[¤
²³g
´:µ:¶>G;ICDGFG@I·>8
e[
¤[
[[
[
[¤[
[[¸
[[ ¤[¤[
¹[[dZ]W][
[¸
[[[ £
[º»»¼½½¾¾¾³¿À»²¿Á¾¿²Á³»Ã½g
¾Äg²ÅÆÀÆgÇÆȲ»gÂÄÆÁƲÅÆÀÆdzgg
JKLKM8@<FADG@¶iµÉU88
e[
¤[[¸
[[ ¤[¤[¹[[dZ]W][
[¸
[
[[[º»»¼½½¾¾¾³¿À»²¿Á¾¿²Á³»Ã½g¾Äg²ÅÆÀÆgÇÆȲ»gÂÄÆÁƲÅÆÀÆdzgg
JKLKM8zJ}{¬zO}U88
h~gÊ
[
¤[£[
[Ë
[¤¤[¢
[¢¤[£[g
g
6~g_­Ì_Í[¤£[g
¡~gV
[Î\Ï[¤[Ðg\[
[Ë[Z[Ðg\[
[
[
[ÐgÑÒ£Ó[ [
[
[
[¤[¤¤£[X[Î\Ï[
[¤
£[] [
[
[
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;87<=>8;?@<A:@8B<B=C;D79E78;8;?=FB?B9B<=C;D797G7<7=7<H;:;I7<7JKL;=AM<NF:@8B<BJB=
IM8NG:@IB<BJO=K
PQMR<B<=Q7<=7:;=@I<B=9;?7:C;=C;D79E7D7<7=L;=C;=QMSQ7<TU=M:CNDN<N=6VJ:;G:;I7<7J=L;=W;A@X:@=
7AX@E:@IB<BJOY=K
Z[K\]SU^\U=I@X@8@?=_O=@CBGB=E;?8@8:@IB<BJ`=QMSQ7<T_=M:CNDN<N=6VJ:;G:;I7<7J=L;=
AM<NF:@8B<BJB=W;A@X:@G@:@8=;9:7D7<C;=IM8NG:@IB<BJO=K
a[KbcdcebfKghihjhkKlO=@CBGB=E;?8@8:@IB<BJ`=QMSQ7<^UT_=M:CNDN<N=6VJ:;G:;I7<7J=L;=
AM<NF:@8B<BJB=W;A@X:@G@:@8=;9:7D7<C;=IM8NG:@IB<BJOK
K
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
m
nopqrspmtuvwvx[yz{|}mm
K
wo~}mM8N:@8B<=FVJG=7F7<=WEEXTTOHM<E8M:M8:COE?T=K;=@D:@<EBAB<C@<=
=
KhKKgK;<;I=I6N:@G@AB=V:G<=?N::@<@8@?=I@8CBG=@:@7:78`=C;<;I=
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
567789:6;6<=89>8?8;>@A=B7;CB?DB;BEB9;:@;<B9@;6<98;FBF>@GB9;CH;:@9@<@;6B>;>@A=B7;CB?DB;CI?JGJ9:@9;
KLMLMNLOLPQNQMRQOQSTUU
U
VWXYZ[Z\Z]^Z_`;:@a@=B9:@7B;6=>G6;b@<6;6c6?G6989;FBF>@G;E878d896;@>7BFB9B;FBF>@G;e@b6C89:67B;
:@aBdBG?@=B;DIc?@G?@<@=@7;6E87?6<898cf;U
ghijklmZ
U
VWXYZnZ\Z]^Z_o;:@a@=B9:@7B;6=>G6;b@<6;6c6?G6989;FBF>@G;E878d896;@>7BFB9B;FBF>@G;e@b6C89:67B;
:@aBdBG?@=B;DIc?@G?@<@=@7;6E87?6<898cf;U
ghijklmZ
U
VWXYZpZ\Z]^U_o;b@;_`;:@a@=?@=B9:@7B;:@aBdBG?@=B9;FBF>@G;e@b6C8989;q=@769F896;96F8?;@>7B;
@>>B7?@=B9B;:@b=@;@?@G69?6=8989;>J=J9J;:@;:JdJ9@=@7;6E87?6<898cf;U
ghijklmZ
U
VWXYZrZ\Z]^UsB=BdB9;q6=7?8;>J=:@7B;Bd6=@>?@=@;76=d8;FBF>@G;E878d89:67B;@>7B?@=B9B9;96F8?;A?:HaH9H;
6E87?6<898cf;U
ghijklmZ
U
VWXYZtZ\Z]^Uua@=;CI<?@;CB=;FBF>@G;G67FBGHG;E878d8;ov;b;b@;GB9BGHG;E878d8;wxyUzU{NLML|U
F898=?6969;CB=;FBF>@G;B?@;>6F6=?69G8d;A?F6;B:B;FBF>@G;E878d896;CH;:H=HGH9;@>7BFB9B;FBF>@G;
DB=BdB9@;H<DH?6:8a898c;FB9JF};JED@9};76=@;b@;~;DB=Bd?@=;BEB9;6<=8;6<=8;6E87?6<898cf;U
ghijklmZ
U
VWXYZZ\Z]^U
UA=>6G89:6;_o;F6CB>;A?G67;Jc@=@;_`9B9;q6=7?8;:@a@=?@=B;b@;_`;F6CB>;
A?G67;Jc@=@;_oB9;q6=7?8;:@a@=?@=B;BEB9;FBF>@G;e@b6C898;76=@;>BB9:@;DB=Bd;BEB9;DIc?@G?@<B9Bcf;
?:8a898c;FA9HE?6=8;<A=HG?6<898cf;U
ghijklmZ
U
VWXYZZ\Z]^U_o;b@;_`;:@a@=?@=B;F6CB>;A?G67;Jc@=@;7@9:B9BcB9;F@E@e@aB;:@a@=?@=:@;I=9@7?@G@;
c6G69898;o;F};fo;F};fo;F;b@;fo;F;:@a@=?@=B9:@;6?6=67;:@b=@;B?@;B?DB?B;FBGJ?6F<A9H;
D@=E@7?@d>B=B9Bc;b@;:@b=@9B9;E878d898;DIc?@G?@<B9BcfU?:8a898c;FA9HE?6=8;<A=HG?6<898cf;U
ghijklmZ
U
0123420
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:9;9:<=>?@ABCDB@EFGGHIAF@J=KFDGLH@MND?@EFOHDLFPHIHO@QRND?LFD@OND@ISTBLSGTB@NLUFLHAHD@CB@
VWOXUXIX@EFOHDLFUFPF@YBDBG@PNGT?DZ@RND?LFD@P?GFDHAFGSLBDABI@KFDGLH@NLF[FGTHDZ@>FMST@MND?LFD@
AB\BDLBIASDUBPB@FLHIUFPF[FGTHDZ]=
^_`abcd9
=
=
=
0112340
TEORĐK BĐLGĐ
Sayfa 1 / 11
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-2.2):
Bir elektrik devresinin zaman domeninde incelenmesi için, önce o devrenin ya entegre-diferansiyel
denklemlerinin, ya da durum denklemlerinin yazılması gerekir. Bu denklemlerin çözülmesiyle
devrenin zaman domenindeki incelenmesi tamamlanır. Bilindiği gibi, diferansiyel denklemlerin
çözülmesiyle ortaya çıkan çözümü iki parçaya ayırmak mümkündür: Çözümün birinci parçasını
devredeki ilk koşullar, ikinci parçasını da devredeki kaynaklar belirler. Çözümün bu parçalarına,
sırasıyla Öz ve Zorlanmış Çözüm adları verilir. Asimptotik kararlı, diğer bir deyişle t →∞ için durum
geçiş matrisinin sıfıra uzandığı bir devrede, t→∞ giderken öz çözüm sıfıra, zorlanmış çözüm de özel
çözüme ulaşır. Daha açık bir deyişle, asimptotik kararlı bir devrede, devrenin incelenmesine
başlanılmasından belirli bir zaman sonra, tam çözüm büyük bir yaklaşıklıkla özel çözüme eşit olur.
Asimptotik kararlı bir devre için tam çözümü, geçici çözüm ve kalıcı (sürekli) çözüm olarak iki
parçadan oluşuyor diye düşünebiliriz. Asimptotik kararlı bir devre için diferansiyel denklem
sisteminin homojen çözümüne geçici, özel çözümüne de kalıcı çözüm denilmektedir. Geçici çözüm,
başlangıçta çok büyük olsa bile, devre çalışmaya başladıktan belirli bir zaman sonra küçülür, sıfıra
yaklaşır. Kalıcı çözüm, devrede kaynaklar olduğu sürece devam edecek çözümdür. Etkisi çok kısa
sürmesine karşın geçici çözüm bir devrede elemanların seçilmesi bakımından önemlidir. Örneğin,
elektrik enerjisi dağıtım sisteminde (şebekede) sistem çalışırken birdenbire meydana gelen arızadan
(kısa devre gibi) dolayı, arızanın olduğu andan itibaren ortaya çıkan geçici çözümün şebekedeki
hatların, cihazların, ölçü transformatörlerinin ve anahtarların seçimi bakımından bilinmesi gerekir.
Eskiden şebekedeki anahtarların “açma zamanlarının” büyük olmasından dolayı, arıza halinde ortaya
çıkan geçici çözümle açma zamanından kısa sürdüğü için ilgilenilmezdi. Bugün açma zamanları
küçük olduğu için geçici çözümle ilgilenilmesi, şebekedeki elemanların seçilmesinde göz önüne
alınması gerekmektedir. Devrelerin zaman domeninde incelenmesi, birçok cihazın çalışma ilkelerinin
ve işlevlerinin anlaşılması bakımından çok önemlidir.
Zaman sabiti elemanı diferansiyel denklemi birinci dereceden olan bir sistemi temsil eder.
Zaman sabiti elemanın transfer fonksiyonun genel yapısı
şeklindedir. Burada T zaman sabiti olup zaman boyutundadır.
Zaman sabiti elemanı tipinde çalışan kapalı-döngü sistemin blok şeması Şekil 5.1a'da verildiği gibi
olur. Sistemin indirgenmiş blok Şekil 5.l b'de verilmiştir.
Fiziksel yapısı ne olursa olsun, zaman sabiti tipinde transfer fonksiyonuna sahip sistemler aynı giriş
karşısında aynı dinamik davranışları gösterirler. Verilen herhangi bir fiziksel sistem için matematiksel
cevap elde edildikten sonra sistemin fiziksel yapısına göre yorum yapılır.
Zaman Sabiti Elemanın Birim Basamak Giriş Cevabı
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 11
r(t)=u(t) birim basamak fonksiyonun Laplace dönüşümü R(s)=l/s olduğuna göre, aşağıdaki
denklemden cevap fonksiyonu
elde edilir. Yukarıdaki denklemi basit kesirlere ayırıp sabitlerini değerlendirerek;
elde edilir. Zaman alanı cevap fonksiyonu c(t) bulmak için terim terim ters Laplace dönüşümünü
alırsak,
elde edilir. Yukarıdaki denkleme göre cevap t=0 başlangıç değerinde sıfır ve
, nihai değerinde
birim değere eşittir. c(t) üstel fonksiyonunda
den
kadar t'ye değerler vererek karşılık
gelen c(t) değerleri çizilirse aşağıdaki cevap eğrisi elde edilir.
Buna c(t) denkleminde t=T koyarak
şeklinde elde edebiliriz.
Bir sistemin zaman sabiti ne kadar küçükse, cevabı o kadar hızlıdır. Üstel cevap eğrisinin diğer
önemli bir özelliği ise t = 0 daki eğiminin l/T eşit olmasıdır. Bunu şu şekilde gösterebiliriz;
Bu ise; eğer sistemin cevabı başlangıçtaki hızını koruyabilseydi t=T de nihai değerine ulaşabildi
anlamına gelir. Aşağıdaki şekilde verilen üstel cevap
Birinci dereceden sistemin cevap eğrisi
eğrisinde c(t) değer t-T de nihai değerinin %63,22'sine ulaşmıştır, Zaman sabitinin iki katı değerinde
(t=2T) cevap eğrisi nihai değerinin % 86,5 ve bunu izleyen t=3T, 4T ve 5T değerlerinde ise sırasıyla
nihai değerinin % 95, %98,2 ve %99,3 değerlerine ulaşır. Matematiksel olarak cevap eğrisi kalıcı-
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 11
durum haline sonsuz zaman aralığı sonunda erişir. Uygulamada ise cevap eğrisi nihai değerin % 98
ulaştığında veya zaman sabitinin dört katı bir zaman sonra yaklaşık olarak nihai değerine ulaşmış
sayılır.
Sistemin kalıcı-durum halinde hata verip vermediğini bulmak için e(t)=r(t)-c(t) den; birim basamak
için r(t)=l ve
olduğundan,
zaman alanı hata fonksiyonu tespit edilir.
Daha sonra
da
değeri bulunduğundan sistemin basamak giriş karşısında herhangi bir
kalıcı-durum hatası vermediği gösterilmiş olur. Bu durum ayrıca yukarıdaki şekildeki eğriden de
görülebilir.
Zaman Sabiti Sistemlerin Birim Rampa Giriş Cevabı
Birim rampa fonksiyonun Laplace dönüşümü
rampa giriş cevap fonksiyonu
olduğuna göre zaman sabiti sistemin
olur. Kısmı kesirlere ayırırsak;
elde edilir ve terim terim ters Laplace dönüşümünü alarak zaman alanı cevap fonksiyonunu aşağıdaki
şekilde elde ederiz.
Yukarıdaki denklemde
den
kadar değerler vererek karşılık gelen cevap eğrisini c(t)
aşağıdaki şekildeki gibi elde ederiz. Sistemin hata sinyali e(t) ise,
Zaman sonsuza giderek meydana gelen kalıcı-durum hatası;
olarak sabit bir kalıcı-durum hatası meydana gelir. Aşağıdaki şekilden de
Şekil 5.3 Birinci dereceden sistemin birim rampa cevabı
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 11
görüldüğü gibi meydana gelen kalıcı-durum hatası T ye eşit olur. Bu durumda sistemin zaman sabiti
ne kadar küçük ise meydana gelebilecek kalıcı-durum hatası da o oranda küçük olur.
Zaman Sabiti Sistemlerin Birim Anidarbe Giriş Cevabı
Birim anidarbe fonksiyonu Laplace dönüşümü R(s)=l olduğuna göre birinci derece sistemin cevap
fonksiyonu
olur. Ters Laplace dönüşümü alınırsa
Şekil 5.4 Birinci dereceden sistemin birim anidarbe cevabı
elde edilir,
denkleminde
den
kadar değerler verirsek
Yukarıdaki şekilde görülen cevap eğrisi elde edilir.
Sistem bir anidarbe giriş uyarısı karşısında sabit değerden başlayarak, kararlı ise zaman sonsuza
giderken üstel olarak başlangıç durumuna geri döner.
Zaman sabiti elemanının indirgenmiş blok diyagramı şu şekilde elde edilir.
Vi(s)=VR (s) + VC(s)
VR(s)=Vi (s) – VC(s)
VC(s)= VO(s)
VR(s)=Vi (s) – VO(s)
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 11
En genel halde cevap;
c(t) = 1 – e-αt
t = 1 aolması durumunda e−at = 1 e = 0.37 olur.
c(t) = 1− 0.37 = 0.63
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 11
Burada 1 azaman sabiti (sn), a üstel frekans (Hz)’dir. Zaman sabiti basamak cevabının son değerinin
%63’üne yükselinceye kadar geçen süreye eşittir. Sistemin kutbunun s düzlemindeki yeri aynı
zamanda üstel fonksiyonun üssünü verir.
Yükselme Zamanı (Tr):
Basamak cevabının son değerinin %10’undan %90’ına ulaşıncaya kadar geçen süredir.
1 – e-at = 0.9 ve 1 – e-at = 0.1 işlemlerinin farkı alındığında Tr bulunur.
Yerleşme Zamanı (Ts):
Basamak cevabının kendi son değerinin %98’ine ulaşıp orada kalıncaya kadar geçen
süredir.
1 – e-at = 0.98
Birinci Dereceli Transfer Fonksiyonunun Deneyle Elde Edilmesi:
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 11
Şekilden cevabın 0.72 değerine oturduğu görülmektedir.
0.72×0.63=0,454
Zaman sabiti elemanının , birim basamak girişe cevabının başlangıç anında sıfır olduğu τ kadar
zaman sonra , erişeceği son değerin % 63.2’ sine vardığı , 4τ kadar zaman sonra % 2’ den daha
küçük bir hata ile son değere eriştiği görülmektedir. Ölçme elemanının zaman sabiti τ ne kadar
küçükse sistemin cevabı o kadar hızlı olacak , son değere ulaşma ve gerçek değeri gösterme zamanı o
kadar azalacaktır.
r(t) = u(t) birim basamak fonksiyonun laplace dönüşümü R(s) = 1/s olduğuna denklemden cevap
fonksiyonu
1
Ts+1
1
C(s) =
s
elde edilir. . Zaman alanı cevap fonksiyonu c(t) bulmak için terim ters laplace dönüşümü alırsak,
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 11
c(t) = 1-e-t/T elde edilir. Denkleme göre cevap t = 0 başlangıç değerinde sıfır ve t = ∞ , değerinde
birim değere eşittir. Bu tür üstel bir eğrinin en önemli karakteristiği ise t = T de c(t) nın 0,632 eşit
olması veya diğer bir deyişle c(t), cevabının ulaşması gerektiği değerinin %63,2 ye ulaşmış olmasıdır.
Buna c(t) denkleminde t = T koyarak aşağıdaki şekilde elde edebiliriz.
c(t) = 1-e-1 = 0,632
Burada T zaman sabiti olup birinci dereceden sistemlerin dinamik davranışı ile ilgili temel bir
parametresidir. Buna göre bir sistemin zaman sabiti ne kadar küçükse, cevabı o kadar hızlıdır. Üstel
cevap eğrisinin diğer önemli bir özelliği ise t = 0 daki eğiminin 1/T eşit olmasıdır. Bunu şu şekilde
gösterebiliriz;
de
1
dt
T
1
=
e-t/T t = 0 =
T
Bu ise; sistemin cevabı başlangıcındaki hızını koruyabilseydi t = T da gerçek değerine ulaşabilirdi,
anlamına gelir. c(t) değer t = T de gerçek değerinin %63,2 sine ulaşmıştır. Zaman sabitinin iki katı
değerinde (t = 2T) cevap eğrisi gerçek değerinin %86,5 ve bunu izleyen t = 3T,4T ve 5T değerlerinde
ise sırasıyla gerçek değerinin %95, 98,2 ve 99,3 değerlerine ulaşır. Matematiksel olarak cevap eğrisi
kalıcı durum haline sonsuz zaman aralığı sonunda erişir. Uygulamada ise cevap eğrisi nihai değerin %
98 ulaştığında veya zaman sabitinin dört katı bir zaman sonra yaklaşık olarak gerçek değerine ulaşmış
sayılır. Sistemin kalıcı durum halinde hata verip vermediğini bulmak için e(t) = r(t) – c(t)den; birim
basamak için r(t) = 1 ve c(t) = 1 – e-t/T olduğundan e(t) = e-t/T zaman alanı hata fonksiyonu tespit
edilir. Daha sonra t
∞ da e(∞) = 0 değeri bulunduğundan sistemin basamak giriş karşısında
herhangi bir kalıcı durum hatası vermediği gösterilmiş olur.
Zaman sabitini 1/RC formülü ile hesapladığımızda
0.001 değerini elde ediyoruz. Deneyimizde bu
değeri 0.00124 olarak ölçtük.
Zaman sabitinin 2 ms olması için Zaman
sabiti=R*C den R=2/10-8 ile direnç değeri
=200Mohm olarak bulunur. Bu değişim sonrası
(R’in yeni değerinden sonra) referans çıkışın
referans değerinin %63’üne ulaşması için (0.002 s)
2 ms’lik bir zamana gerek vardır.
Matlap aracılığı ile bu sistemi oluşturduğumuzda 1V değerindeki basamak girişe karşı
aşağıdaki çıkışı elde ederiz.
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 9 / 11
Bu
sistemin
transfer
fonksiyonu
ise
olarak bulunur.
9
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 10 / 11
Zaman Sabiti elemanın step’e cevabı
Sistemin zaman sabiti
dir. Bu durumda olur. Vin=1V kare
dalga uygulandı ve aşağıda görülen çıkış alındı. Vo ın 0.63 V değerine ulaşması için geçen süre
osilaskopun kursör özelliği kullanılarak 1.16 ms olarak ölçüldü. Buradan Vo ın 0.63 V değerine
ulaşması için 1.16 τ lık zaman geçmesi gerektiği anlaşılıyor.
Sistemin zaman sabitini 2ms yapmak için R=200kΩ yapıldı.
dir. Vin=1V kare dalga uygulandı ve aşağıda görülen çıkış alındı.
Vo ın 0.63 V değerine ulaşması için geçen süre osilaskopun kursör özelliği kullanılarak 2.32 ms
olarak ölçüldü. Buradan Vo ın 0.63 V değerine ulaşması için yine1.16 τ lık zaman geçmesi gerektiği
anlaşılıyor.
10
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 11 / 11
Yukarıdaki şekillerde çıkış vevabındaki üstteki doyum RC sisteminin giriş işaretinin frekansının çok
büyük olmasına ve buna cevap vermede yavaş davranmasından dolayı kaynaklanmaktadır. Eğer giriş
işareti frekansı düşürülürse cevabında belli bir değere oturduğu rahatlıkla görülebilir.
MATLAB ile RC sistemi modellenmek ve basamak cevabı görülmek istenirse aşağıdaki komutlar
icra edilecektir.
>> R=100*10^3;
C=10*10^-9;
pay=1;
payda=[1/(R*C) 1];
>>
>> S=tf(pay,payda)
>> step(S)
>> grid
DEĞERLENDĐRME:
ile verilen transfer fonksiyonuna sahip olan devreye birim basamak
uygulandığında
cevabı alınacaktır. Burada τ = R.C değeri ∞ değerini alınca
olacaktır. Burada C(t) = Vo olarak alınmıştır. Yani sistemin genliği birim basamak için
daima 1 dir. R nin değişimi Vo ın dalga şeklini geçici rejimin süresi açısından değiştirir. Geçici
rejimin süresi τ cinsinden değişmez.
R değerini (enerji harcayan elemanın değerini) arttırınca sistem daha geç cevap vermeye başlar. Bu
durumda zaman sabiti artacaktır. Daha önce referans değerinin %63’üne 1 ms değerinde ulaşırken, bu
sefer bu süre 2 ms olmuştur. Burada zaman sabitine hangi (R C) parametrelerin etki etiğini ve zaman
sabitinin sistem üzerinde nasıl bir etki ettiği gözlemlenmiştir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
11
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_02/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDEFGFHIDHJKLDMNFHLDOFPHGDIQRST
67879:8@:B:UVUV::
67879:?@8=A=:B:WXYXZ[\X]^_^[`ab[cdedfdg[hidYXZj[k^l^Zmdn^[\^o_dY^Z[pdqX]j:
67879:rsrtuB::
vwTxyzy{T|y}~~T
H
H
HGTHMHHHHH
yT|~y|yT~{zT
UwTH
HH
H
HH
HH
H HT
¡wT¢
H£H
H
HH£HH£H
H¤
H£HHH¤
H
H¥Hy¦yzyTT
§wT¢
H£H
H
H£H
H
¨Ḧ{|~©{ª{ªT©y«y}~zT
67879:7¬7sr8¬r<uB::
­HH­®®HM¯H
¥°H­HH­®H
T
ch±h²[³´µ¶·³¸³\µ¹[:
RH
¥HHHHH¥
H£H
Hº£H£
Hȴ
H¥H
¼
H
HQGJDJHHº£H£
HH»¤H½¾¿¿ÀÀÀ{¦À¦Á¿T
À}TyÁ¦|~{~T«~©y¦TÁ}~~¦|~{~«TT
67879:\¸÷³\²Ä±ÅB::
RH
¥H
Hº£H£
Hȴ
H¥H¼
H
HQGJDJHHº£H
£
HH
H½¾¿¿ÀÀÀ{¦À¦Á¿TÀ}TyÁ¦|~{~T«~©y¦TÁ}~~¦|~{~«TT
67879:r6us¬r<uB::
vwTÆH¥H
¤°HÇH¥¥H
¨H¨
¥
HH¤
H£
H
H£
¤ HT
T
UwTCHÈI
ÉHÊTIHH
HÇTÊTË̤ÍTHH¥¥
¤°H»¥
H
HGHH¥
¤H
HÈMH
H¨
H
H
¤HH
£¥£
¤ HQ
°H»»H¨
HHÇH É HE
H
H
¤
¤HH
¤H¥¥
¤HÈRyÁyT}~¦T«yzy{T|y}~~T~~T|~|zT~{{zTT
H£HH£H
HRHHGH¥H£HH
H
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=<;:>?8@A@:B<C<DE9F:G8H@IA@:E<;J@F:K9;98@H78L;A9;:MN:><8:D@89:A@F6@:H<O<;A9:<P@89H:
QRSQTU;AVWV:X@DDV;A@:JG8?I:J@OV;VCYZ:[[
\][^E<F@EDG>?;:DL8E78:7C9FF<W<;<:D?FF@;@8@D:_G`;V;:aZbc:_GFH:A9W98<;9:?F@PI@EV:<=<;:69=9;:
EL89J<:>?F?;?Cd:X9E@O:JGF?JF@:9FA9:9HH<W<;<C:C@I@;:E@><H<:A9W98<JF9:D@8PVF@PHV8V;VC:e9:
EG;?=F@8V;VCV:JG8?IF@JV;VCZ:[
f][g@I@;:E@><H<;<;:h:IE:GFI@EV:<=<;[6989DF<:i:A<89;j<;<;:A9W98<;<:X9E@OF@JV;VC:e9:i`;<;:
A9W98<;<:>?:A9W989:@J@8F@J@8@D:hZ:e9:cZ:@AVIF@8V:H9D8@8F@JV;VCZ[
[
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
k
lmnopqnkrstutv]wxwyzkk
[
um{zk|G8?F@8V;:=7CLIL:<=<;:XHHO}~~ZjG;H8GFG8FAZHD~:[9>:>@WF@;HVEV;A@;:MN||:
[U[Q[R[9;9J:J6?F@I@EV:>7FLIL;L:D?FF@;@8@D:J@8AVI:@F@><F<8d:A9;9J:
X@DDV;A@:@J8V;HVFV:H9G8<D:><F6<:<=<;:A9:J<;9:@J;V:E<EH9I<;:>?:A9;9J9:@<H:H9G8<D:><F6<:>7FLIL;A9;:
RUUTUUT[[
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
6789:;:<:=>5?@ABCBDEFABGE@HDIJK@LBMH@HNHOPHFJF@QJGJKIH@FHRJO@SED@ABCEKEPB@RBSBT@UOAVCVFV@
HQJGOHMJFJNW@XOAJCJFJN@RUFVQOHDH@YZDB@QJGJKIHGE@ABCEKEP@EOB@NHPHF@RHSEIE@HDHRJFAHGE@EOEKGEME@
MUDVPOHMJFJNW@5
[\]^_`a:
5
6789:b:<:=>5?@ABCBDE@RHSEI@GHOPHG@cNBDB@RERIBP@QJGJKJFAH@deABGE@HDIPH@LBMH@HNHOPHFJF@UIVDPH@
NHPHFJFJ@BIGEREFE@HQJGOHMJFJNW@5
[\]^_`a:
5
6789:f:<:=>5gERIBPAB@hWi@NHPHF@RHSEIEFAB@?jkh@Fl@UOPHG@cNBDB@UIVDPH@NHPHFJFJ@RERIBP@
mBLHSJFJ@YZNOBPOBMBDBG@MUDVPOHMJFJNW@5
[\]^_`a:
5
6789:n:<:=>5d@LB@?@ABCBDOBDEFABGE@HDIPH@LB@HNHOPHRJ@AVDVPVFAH@RERIBP@QJGJKJFAHGE@o5pqrqs5
tquvwv5xy5UIVDPH@NHPHFJ@GDEIBDOBDEFB@BIGEOBDEFE@HMDJ@HMDJ@HQJGOHMJFJNW55
[\]^_`a:
5
6789:z:<:=>5gERIBPAB@{@NHPHF@RHSEIE@UOPHG@cpy|y5o}~5t5o}~5t5o}5t5LB@{jkWi@UOPHG@cNBDB@
ZFmB@d@RHSEI@GHOPHG@cNBDB@HDGOJ@?@ABCBDOBDE@EQEF@LB@AHH@RUFDH@?@RHSEI@GHOPHG@cNBDB@HDGOJ@d@
ABCBDOBDE@EQEF@SV@RERIBPEF@PHIBPHIEGRBO@PUABOEFE@
o5UDIHPJFAH@UOVKIVDHDHG@BD@SED@
AVDVP@EQEF@SHRHPHG@YEDEKB@UOHF@RERIBP@mBLHSJFJ@YZNOBPOBMEFENW@XOAJCJFJN@RUFVQOHDJ@
MUDVPOHMJFJNW@5
[\]^_`a:
5
6789::<:=>5d@LB@?@ABCBDOBDE@RHSEI@UOPHG@cNBDB@GBFAEFENEF@RBQBmBCE@ABCBDOBDAB@ZDFBGOBPB@
NHPHFJFJ@k@R@hWk@R@hWhk@R@LB@hWhhk@R@ABCBDOBDEFAB@HOHDHG@ABLDB@EOB@EOYEOE@REPcOHRMUFV@
YBDQBGOBKIEDEFEN@LB@ABLDBFEF@QJGJKJFJ@YZNOBPOBMEFENW@XOAJCJFJN@RUFVQOHDJ@MUDVPOHMJFJNW@5
[\]^_`a:
5
6789:=:<:=>5V@ABLDB@HGGJFAH@5HDGOJ@RUDV@HNJDOHMJFJN@gUDVOHD@NUD@FEIBOEGIB@UOPHOJAJD@LB@
QZNcPcFc@HNJDOHPHMH@YBDBG@MUGIVDW@gUDVOHD@MVGHDJAHGEOBDABF@HDGOJ@UOHmHGIJDW@HREI@RUDVOHD@
ABCBDOBFAEDPBMB@HOJFPHMHmHGIJDW5
[\]^_`a5
5
5
0123240
TEORĐK BĐLGĐ
Sayfa 1 / 10
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-2.3):
Vo / Vin =(1 / R + SL)(1 / SC) / 1 + (RSC + S2LC) = 1 / S2LC + RCS + 1
Buna göre transfer fonkisyonu
olarak elde edilebilir.Bu durumda Wn şu şekilde hesaplanır:
Wn = 2 π f = 2*3.14*50 ise Wn=314 olarak hesaplanır.
2 ζ Wn = R / L ise ζ = (4.7 * 103) / 2 * 314 * 33*10-3 =1.91 olarak hesaplanır.
Sönüm oranının 0.7 volt olması için gerekli R değeri;
R= 2 * 0.7 * 37113.48 * 33*10-3 = 1714.64 Ω
Vp=3.3V ve Vin=2V iken aşımın 1V , Vin=1V iken aşımın 0.5V olduğu gözlemlendi. Giriş
geriliminin değişmesi ζ ve Wn değerini etkilememiştir. Bunlar ancak R.L.C değerleri ile değişiyor.
Vin=1V iken osiloskopta Vp=1.04V olduğu yani aşımın 0.04V olduğu görülmüştür.
Sönüm oranı 0.7 iken elde edilen titreşimli sinyalin zaman düzlemi kriterleri:
Maksimum aşma:
mp = e –π ζ / √1- ζ 2 = 0.0455 V
Aşım zamanı:
π / Wd = 1.18*10 -4 sn
Gecikme zamanı:
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 10
(1 + 0.7 ζ ) / Wn = 4.01 * 10 -5 sn
Yükselme zamanı:
1 / Wd tan -1 (- (√1- ζ2) / ζ ) = 1.7*10-3 sn
Oturma zamanı:
% 2 kriterine göre oturma zamanı = 4 / ζ Wn = 1.54 * 10 -4 sn
% 5 kriterine göre oturma zamanı = 3 / ζ Wn = 1.15 * 10 -4 sn
Sönüm oranı 1 yapan R değeri:
R= 2 * 1 * 37113.48 * 33*10-3 = 2449.48 Ω
Bu devrenin durum denklemleri,
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Osilaskopta 0<
Sayfa 3 / 10
<1 için titreşimli aşağıdaki gibi bir cevap görülecektir.
Eğer
değeri daha çok 1'e yaklaşırsa aşağıdaki cevapta görüldüğü üzere titreşimler azalır ve sistem
daha çok sönümlü bir hal alacaktır.
Transfer fonksiyonu :
Yukarıdaki blok diyagram indirgenirse aşağıdaki kapalı çevrim blok şema elde edilecektir.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 10
Sistemin transfer fonkisyonu
olarak karşımıza çıkar.
Titreşim veya salınımlı cevap yapısı özyapısal denklemi ikinci dereceden olan sistemin özel
halidir. Titreşim elemanı sistemin transfer fonksiyonunun genel yapısı aşağıdaki biçimdedir;
burada
[rad/sn] sistemin doğal frekansı,
sönüm oranıdır.Doğal frekans ve sönüm oranı ikinci
dereceden sistemin dinamik davranışı ile ilgili temel parametredir. <1 durumunda sistemin dinamik
davranışı sönümlü salınımlı veya sönümlü titreşimlidir denir.
Birim basamak fonksiyonu uygulanan bu sistemin cevap fonksiyonu aşağıdaki biçimde elde edilir.
Bu ifadenin Ters laplace dönüşümünden sistemin zaman alanı cevabı c(t) elde edilir. Ters
laplace dönüşümü ise sistemin
şeklinde tanımlanan özyapısal denklemin
çözümüne bağlıdır. Đkinci dereceden olan özyapısal denklemin 2 adet kökü ise ;
Sönüm oranın değerine bağlı olarak köklerin durumunu ve buna bağlı olarak sistemin
göstereceği dinamik davranışı aşağıdaki şekilde belirleyebiliriz;
•
ise
kökleri karmaşık eşlenik olup s düzleminin sol tarafında yer alırlar.
Dinamik davranışı açısından sistem sönümlü titreşimli veya az sönümlü adını alır.Bu durumda
kökler aşağıdaki şekilde ifade edilir.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 10
Buna göre sistemin ters laplace dönüşümünden sistemin zaman alan cevabı matematiksele ara
işlemlerden sonra düzenlenirse;
•
ise
kökleri gerçek ve birbirine eşit olup kökler
dir.Sistem dinamik
davranışı açısından kritik sönümlüdür.Cevap eğrisi titreşim göstermez.Bu durumda ilk
denklemin ters laplace dönüşümünden sistemin zaman alanı cevabı aşağıdaki şekilde elde
edilir ;
•
ise
köklerinin her ikisi de ilk ksi değerindeki gibi negatif olacaktır.Bu durumda
sistemin cevabı aşağıdaki biçimde olur;
Dinamik davranışı açısından sistem titreşimsiz ,aşırı sönümlüdür.Cevap hızı yavaştır.
•
ise
kökleri eşlenik sanal olup sanal eksen üzerinde yer alırlar.
olur.
Sistem sönümsüz titreşimli dinamik davranış gösterir.sistemin cevabı ise aşağıdaki şekilde olur;
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Değişik
Sayfa 6 / 10
değerlerine karşılık gelen eğriler aşağıdaki biçimdedir;
sistemin transfer fonksiyonu 2. dereceden sistem;
=sönüm oranı
Denklemi benzetmek için s2 yalnız bırakılır.
V0(s) / Vin(s) = (1/LC) / [ s2 + s(R/L)+ (1/LC) ]
wn2 = (1/LC) = 1 / (33x10–3)(22x10–9)
wn =37113.48
2ζ wn = R/L
ζ = 1,92
2ζ(37113,48) = (4,7x103) / (33x10–3)
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 10
Vo(s)/Vin(s)=(1/LC)/(s2+sR/L+1/LC) olur. => 2 Wn=R/L olur. Wn2=1/LC olur.
=0.7 olması için R değeri hesaplanır.
=R/2*
R=0,7*2*
=1714 ohm bu kadarlık direnç devreye takılır.
ln Mp=ln e (-
/
)=0,049
Wn=
tp=
=37119 rad/s
/Wn
)=3,14/37119*
tr=1/Wd*tan (-
/ )=79
=118
s
s
%98 için ts=4* / *Wn=154
s
Yukarıda hesaplanan değerlerdir. Yani devreye 1714 ohm luk 1 pot takıldığı zaman hesaplanan
değerlerdir. Aşağıda da devrede ölçülen değer osilaskobun cursor özelliği ile alındı.
Mp=0,045
tr=87
s
tp=107
s
ts=165
s
Ölçüm ve hesaplanan değerler birbirine yakındır.
Sönüm Oranı
R=1*2*
=1 olduğu zamanki direnç değeri
=2450 ohm
Bu değerdeki direncin oturma zamanı ts=204
s
Çıkışa 1V genlikli kare dalga uyguladığımızda, çıkışta aşağıdaki sinyali elde ederiz
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 10
Sönüm oranının (ζ) 0,7 olması için gerekli R
2(0,7)(37113,48)=R/(33x10–3)
R=1714 Ω
Titreşimli sinyalin zaman düzlem kriterlerini (Maximum aşma, aşma zamanı, ölüm zamanı yükselme
zamanı, oturma zamanı) aşağıdakiler gibidir.
ζ= 0,7
tg = (1 + 0,7 ζ ) / wn
µp = e πζ / (√1-ζ2)
tg = 40µs Gecikme zamanı
µp = 4,6 Max. aşım
wn = 37113,48
wd = 26504,33
ta = π / wd
ta = 119 µs Aşım zamanı
ty = (1 / wd) tan–1 –[(√1- ζ2 )/ ζ ]
ty= 30 µs Yükselme zamanı
σ = ζ wn
σ =25979,44
to = 4/σ
to = 154 µs Oturma zamanı
Sönüm oranını 1 yapan R değeri :
2 (1) (37113,48) = R/(33x10–3)
R=2450Ω
R direncinin değeri sönüm oranının 1 olduğu değere gelene kadar ayarlandığında sistem kritik
sönümlü hale geçer. Titreşim azalır.
MATLAB ile RLC sistemi modellenmek ve basamak cevabı görülmek istenirse aşağıdaki komutlar
icra edilecektir.
>> R=4.7*10^3;
L=33*10^-3;
C=22*10^-9;
pay=1/(L*C);
payda=[1 R/L 1/(L*C)];
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 9 / 10
>>
>> S=tf(pay,payda)
Transfer function:
1.377e009
----------------------------s^2 + 1.424e005 s + 1.377e009
>> step(S)
>> grid
2. mertebeden sistemler ile ilgili formüller aşağıdadır. Bu formüller ile ilgili kısaltmalara ilişkin
sembollerin anlamları şöyledir:
e: Eular sabiti (e sayısı, 2.717)
Mp: Aşım miktarı
% Mp: yüzde aşım
tg: Gecikme zamanı
ta: Aşım zamanı (s)
to: oturma zamanı (%5 ve %2 hatalar için ayrı ayrı)
ty: yükselme zamanı
Wn: Doğal frekans (rad/s)
Wd: Wn'nin sinüs bileşeni
T(to): Zaman sabiti
zeta (kısi): Sönüm oranı
B (beta): ty hesaplaması için kullanılan sabit
Bu sistemler hakkında ve yukarıdaki formüller ile ilgili detaylı bilgi almak için lütfen bu bağlantıdaki
dökümanı inceleyiniz.
DEĞERLENDĐRME:
Bu devrenin transfer fonksiyonundan onun 2.dereceden bir sistem olduğunu anlıyoruz. Bu
devrenin titreşim yapıp yapmayacağını sönüm oranı (ζ) belirlemektedir. Sönüm oranını bulurken ilk
başta sistemin doğal frekansı (wa) bulmamız gerekmektedir. L ve C elemanlarının değerleri sabit
olduğunda deneyimimizde wn de bunlara bağlı olduğundan deney boyunca hiç değişmemektedir.
Fakat sönüm oranı R ve L elemanına bağlıdır. L elemanı sabit olduğundan R’yi değiştirerek sönüm
oranını da değiştirebiliriz. R yi sönüm oranını 0,7 yapacak değere getirdiğimizde b değerine sahip
sistem az sönümlü haldedir ve titreşim yapmaktadır, fakat kararlıdır. R yi sönüm oranı 1 olana kadar
ayarladığımız da ise titreşimler oldukça azalır. Bu duruma kritik sönümlü hal denmektedir. Sistem
kararlı haldedir. R yi azalttığımızda ζ değeri de azalmakta ve sistemdeki titreşimler artmaktadır ve
sistem kararsızlığa doğru gitmektedir. R yi kısa devre ettiğimizde ise R değeri 0 olacağı için ζ
değeri de 0 oldu. Böyle bir durumda ise sistem sürekli bir osilasyon yapmaktadır. Sistem sönümsüz
hale geçmiştir ve artık sistem kararsızdır.
9
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 10 / 10
Sistemde R değeri azaldıkça titreşim miktarı artmakta, R 0 olduğunda sistem kararsız olup
sürekli titreşim yapmaktadır. R değeri azaldıkça, sönüm oranı azalmakta, max aşım artmakta,
yükselme zamanı azalmakta, oturma zamanı artmaktadır.
Sistemde R değeri arttıkça sönüm oranı artmaktadır. Buna bağlı olarak max aşım azalmakta,
yükselme zamanı artmakta, oturma zamanı kısalmaktadır. Kısaca sistem daha az aşım ile daha erken
cevap vermektedir.
Sonuç olarak, R değerinin artması sistemin titreşimlerini azaltmakta ve kararlılığını
arttırmaktadır. Bunun yanında, R nin azalması titreşimleri arttırmakta ve sistem kararsızlaşmaktadır.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
10
http://mu.controlworld.tk/control/experiments/auto_control/experiment_02_03/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDEFGFHIDHJKLDMNFHLDOFPHGDIQRST
67879:8@:B:UVWV::
67879:?@8=A=:B:XYZ[\]Y^_`a\^bcd_efgh\[\i\j_XYkYcl\mY_nYoZ\^Yc_p\qbrd:
67879:stsuvB::
wxTyz{|}~zH}}H{zz
}zHz{}}|zHGH}HM|}HHz|z~}|}H|~H}|}}zH
}|HzHz}}}T
UxT|H
z|}HzH}H
{|H
}}|}|z}H|}H~H~H}{zzzH|HT
WxTHz{zH|H|}}H}HH{zHz|Hz{}zHHz{zH}H{|HH
|
zHzz~zzHz}z}HT
xTyz{|}~zH}}H{zz
}zHz|Hz{}zH{|}|HzHz}T
xTH}H}{H||H|}}z}HT
xT}{H
}}|zzHz{}H}|z
}zH}{z}|zzHz}z}HT
xTJz{}H||HH{z{|}~zH
|HzzH|
H|Hz}HT
xT ¡¢£¡¤T|{
Hz{}zH
}}}zzH}HzHH|}}T
67879:7¥7ts8¥s<vB::
¦H
}{H§¨H}H¦©HMªH{z}{|}H¦H
}{H««H¬H¦H
}{H­­HT
h`®`¯_°±²³´°tsAvB::
RH
}}Hz}HzzzH{}|zH}H|{Hzz}|HzzHµ}H{HzHH
z¶HHQGJDJHz{}zHµ}H{H~H}|}H·¸¹̧º»»¼¼¼½¾¿ÀÁ̧¿Â¼¿ÁÂýÄ̧»T
¼ÅÆTÇÃÁÅÈÉÀÉTÊÉËÇÁÅŢÅÃÅÆÉÂÉÁÈÉÀÉʽTT
67879:nÌÍδ°n¯Ï®ÐB::
RH
}}HzzHµ}H{HzHHz¶HHQGJDJHz{}zHµ}H
{H~HzzH·¸¹̧º»»¼¼¼½¾¿ÀÁ̧¿Â¼¿ÁÂýÄ̧»T¼ÅÆTÇÃÁÅÈÉÀÉTÊÉËÇÁÅŢÅÃÅÆÉÂÉÁÈÉÀÉʽTT
67879:s6vt¥s<vB::
wxTÑ}z
}zH
}|}zH|HÒ}HH{|}|HzHz}HH|HÓÔÕH}H
H
|}HÓÕH
}}|}|zzHHT
T
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;:<=>?@:AB>C8@DEF>F=G=>H=I=;:A=>JKL:G>M>NOPQE:R>RK;=>HKESK>TUSTEKUVAVPW>J:XYEKJUDA>
D;FKXVAHK>Z[>:<K;=F>TUSTEKXKAVP>\A=;:E:;>?NK;=>HKESKAVA>];=RKAJ>H=I=;:A:>R=AH:A:P>H=>
^=E:;E=U=^:E:;J:A:P_>`AaKRW>HY<YR>];=RKAJ>H=I=;E=;:>F=;a:L>=H:EX=E:H:;_B_>bVRV<VA>H=I:<:X:A:>
c:P:A:P>d=>JDATcEK;VAVPV>UD;TXEKUVAVP>?eT;Kfg8hij8kglgm8nghioi8oipqi8ninorl8imsrqrmlrtor8ur8
KJEVAHK>^KJKXKR>S:;:<>a=dK^V>:Aa=E=AX=RF=H:;_>eKJKXKR>S:;:<>Z[>J=d:U=E:>^:;>:<K;=F>DEHTITAK>
S\;=>A:c:A>^T;KHK>]:P:RJ=E>D;FKXHK>J:AUKE>v=A=;KF\;YAH=A>`[>^:;>RK;=>HKESK>F:G:AH=>:<K;=F>
wxywqgAHVIV>LKRRVAHK>UD;TX>UKGVAVPB_>8
z78{\AYX>D;KAVAVA>?>|>B>}_~>DEXKJV>:c:A>S=;=RE:>>H=I=;:A:>L=JKGEKUVAVP>d=>U:>L=JKGEKHVIVAVP>
H=I=;=>KUK;EKUK;KR>H=d;=U=>FKRVAVPW>F:F;=<:XE:>^:;>cVRV<>J:AUKE:>=EH=>=FF:I:A:P:>S\PE=XE=U:A:P>d=>
J\AYX>D;KAV>:E=>:E:<R:J:A:>HY<YA=;=R>JDATcEK;VAVPV>UD;TXEKUVAVP8`U;VaKW>DJ:EKJRD^TA>H:I=;>
RKAKEVAK>HK>S:;:<>:<K;=F:>^KIEKUK;KR>DJ:EKJRDG>=R;KAVAHK>S\JF=;:A:P_>ZKLK>JDA;K>L=X>S:;:<W>>
L=X>cVRV<>J:AUKEE=;:A:>DJ:EKJRDG>=R;KAVAHK>cKRV<FV;K;KR>S:;:<>d=>cVRV<>:<K;=FE=;:>K;KJVAHK>UD;TX>
UKGVAVP>?J:EKJRDGFK>S\PE=XE=H:I:A:P>F:F;=<:XE:>J:AUKE=>H:RRKF>=H:E:;J=>D;FKHK>:R:>]K;REV>];=RKAJ>
HT;TXT>dK;HV;_>9:;:<>J:AUKE:A:A>^:;>];=RKAJV>dK;HV;_>`AaKRW>cVRV<>J:AUKE:A:>H=>S:;:<F=A>
RKUAKREKAKA>^:;>];=RKAJVW>KAaKR>S:;:<=>S\;=>F:F;=<:XE:>DEKA>S=c:a:>;=v:X:A>H=>J\AYXEY>DEK;KR>
^:;>];=RKAJV>J\P>RDATJTHT;_>eT>:R:>];=RKAJ>K;KJVAHK>UD;TX>UKGVAVP>d=>A:c:A>]K;REV>H=I=;E=;=>
JKL:G>DEHTITAT>KcVREKUVAVP_B88
78EH=>=FF:I:A:P>F:F;=<:XE:>J:AUKE:A>PKXKA>HYPE=X:>R;:F=;E=;:A:>?XKRJ:XTX>K<XKW>K<VX>PKXKAVW>
\EY>PKXKAW>S=a:RX=>PKXKAVW>UYRJ=EX=>PKXKAVW>DFT;XK>PKXKAV
8rl8rngp8xqwxqg8rl8fr8
DJ:EKJRD^TA>RY;J\;>\P=EE:I:A:>RTEEKAK;KR>^TETATP>d=>JDATcEK;VAVPV>RK;K;EVEVRW>J\AYXEYEYR>d=>
F:F;=<:XE:E:R>KcVJVAHKA>UD;TXEKUVAVP_>8
78>H=I=;:A:>K;FFV;VAVPW>cVRV<>HKESK><=RE:>AKJVE>^:;>H=I:<:X=>TI;KHV>U:>KUK;EKUK;KR>J\AYX>
jgAVAV>M>UKGKA>>H=I=;:A:>L=JKGEKUVAVP>d=>J\AYX>D;KAVAVA>^T>H=I=;:A:>J\AYXEYEYR>d=>
F:F;=<:XE:E:R>KcVJVAHKA>UD;TXEKUVAVP_>8
78>H=I=;:A:>KPKEFVAVPW>cVRV<>HKESK><=RE:>AKJVE>^:;>H=I:<:X=>TI;KHV>U:>RVJK>H=d;=>=H:A:PW>cVRV<>
HKESK><=RE:>AKJVE>^:;>H=I:<:X=>TI;KHV>`EHVIVAVP>JDATcEK;V>UD;TXEKUVAVP_8
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
0123450
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
6
789:;<9=>?@A@BCDEFGH==
6
A8IH=JKLMNOLPQRSTUVWVRXSXQRYZZ[\]]^^^_`KQZLKN^KLNa_Zb]R6^cdRdOeNOQZPfPQaOQRghJiJR
jkjlmnkom6pkl6qr6smomtko6uvcQcwRxwyMNOWOfPuRdTNVWVQVRbMNNOQOLObRwOLaPWRONOdXNXLzRacQcwR
YObbPQaOROwLPQZPNPRZcKLXbRdXNyXRXSXQRacRwXQcROwQPRfXfZcWXQRdMRacQcwcROXZRZcKLXbRdXNyXRdTNVWVQacQR
tp{p{|popqk|k{jkok}~66
6
7===C6
XUXbfcNRacQcwRKLZOWPQaORRacecLXQXQRRwO[PNWOfPQORLOeWcQRXUXbfcNRfXfZcWR
SPbPPQaORZXZLcXWRyTLVNWcwcRacOWRcZWcbZcaXL_RMRaMLMWMRUcZORacecLXQXRacRyTURTQVQacR
dMNMQaMLOLObRcRacLcRcNcWOQNOLPQPQRcZbXNcLXQXRaVVQcLcbROSPbNOwPQPU_R6
=
6
7=D==C6RcRhRacecLNcLXQacbXROLZPRcwOROUONWOQPQRSPbPZORQOfPNRdXLRaceXXWcRfcdc[R
KNaMeMQMROSPbNOwPQPU_RgNaPePQPURfKQMSNOLORyTLcRSPbPZObXRaceXXWRXNcRUcZORacecLXROLOfPQaObXR
XNXbXwXRwKLMWNOwPQPU_R6
=
6
7=F==C6RcRhRacecLNcLXRfOdXZRbONWObRVUcLcRfXfZcW6SPbPPQaORROPWRwO[WObRVUcLcRRcR
UcZORacecLXQXRdMNMQMU_R6
=
6
7===C6JXfZcWacR_RfTQVWRKLOQPQaORwO[PNOQROPWRWXbZOLPzROPWRwVUacfXzRQRcRhR
acecLNcLXQXRdMNMQMU_R_RzRW R6
=
6
7=¡==C6zRRcRhRacecLNcLXQXQROLZWORcROUONWOfP6aMLMWMQaORfXfZcWRSPbPPQaObXRaKeONR
LcbOQfORQ RcZbXNcLXQXROwLPROwLPROSPbNOwPQPU_R6
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=
>
?@AB=C=D=EF>GHIJKLMKNOKJPQRSNOKJPQRTUSNOKJPQVNWKNOKJPQVTUNXYLPZN[OK\KNIK]JH^H_HON`K\`P_aHN
bScNWKNdNMK^K\YK\H_KNae\KNPf\gNPf\gNhijkil>X\JPLg_MPNLXMKYYKfH_HONWKNmnonpnq>aH\HrKNXYP_N
sKWPtg_gNaeOYKLYKfH_HOTNuYMg^g_gONIX_v]YP\gNfX\vLYPfg_gOTN>
6789:;<=
>
?@AB=w=D=EF>bSNcNWKNdNMK^K\YK\HNIPtHJNXYLPZN[OK\KNZK_MH_HOH_NIK]KsK^HNMK^K\YK\MKNe\_KZYKLKN
OPLP_g_gNVNISNRTVNISNRTRVNINWKNRTRRVNINMK^K\YK\H_MKNPYP\PZNMKW\KNHYKNHYaHYHNIHL[xnoyz{|>
aK\]KZYKrJH\H_HONWKNMKW\K_H_N]gZgrg_gNaeOYKLYKfH_HOTNuYMg^g_gONIX_v]YP\gNfX\vLYPfg_gOTN>
6789:;<=
>
?@AB=E=D=EF>}vNMKW\KN`PZZg_MPN~>P\ZYgNIX\vN`POg\YPfg_gONGX\vYP\NOX\N_HJKYHZJKNXYLPYgMg\NWKN
]eO[L[_[N`POg\YPLPfPNaK\KZNfXZJv\TNGX\vYP\NfvZP\gMPZHYK\MK_NP\ZYgNXYPsPZJg\TN}PIHJNIX\vYP\N
MK^K\YK_MH\LKfKNPYg_LPfPsPZJg\T>
6789:;<=
>
>
>
0123450
TEORĐK BĐLGĐ
controlworld.tk
FastQuiz Exam System
Sayfa 1 / 9
Web MWS System
Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-3.1):
Açık - kapalı kontrol cihazı set değeri üstünde veya altında ayar değişkenini açar veya kapar. Kontrol
cihazının çıkışı iki konumludur;ya tamamen açık, ya da tamamen kapalıdır. Örneğin ayar değişkeni elektrik
enerjisi olan sistemde kontrol cihazı, set değerininaltında elektrik enerjisini sisteme tamamen verir, set değerinin
üstünde ise tamamen keser veya tam tersi düşünülebilir.
Açık-kapalı kontrolda kontrol altında tutulan değişken örneğinin sıcaklık, sürekli salınım halindedir. Set
değerinin etrafında salınır. Bu salmımda tepeden tepeye değişim ve salınım sıklığı proses karakteristiklerine
bağlıdır.
Gerek ucuz ve gerekse basit olmalarından dolayı endüstriyel ve evsel ortamlarda oldukça fazla kullanılmaktadır.
ON/OFF kontrolörün iki durumu vardır:
(1) e > 0, kontrolör çıkışı maksimumdur.
(2) e ≤ 0, kontrolör çıkışı minimumdur.
Aşağıdaki şekilde verilen ON/OFF kontrolör genellikle zaman sabitesi uzun olan hidrolik, sıcaklık ve bazı
mekanik sistemler için elverişlidir.
M kontrolörün fiziksel olarak ulaşacağı en büyük değer olmak üzere kontrolör,
u=M.sgn(e)
olarak çalışır ve genellikle Bang-bang kontrolör olarak da adlandırılır.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 9
Kapalı çevrimli
ON/OFF kontrol
sistemi.
Bir ON/OFF
kontrol sisteminin
karakteristiği aşağıdaki şekilde gösterilmiştir. Örneğin üstteki şekildeki sistem, fırının ortam sıcaklığını ölçen bir
sistem olsun. Başlangıçta e > 0 olduğundan kontrolör ON olacak ve sıcaklık exponansiyel olarak hedeflenen
ortam sıcaklığına ulaşana kadar ısıtma işlemi sürecektir. Hedeflenen sıcaklık derecesine gelince e = 0 olacak ve
kontrolör OFF durumuna geçecektir. Fakat ısınma sisteminin zaman sabitesinden dolayı ısınma işlemi bir miktar
daha devem edecek ve belli bir noktaya erişecektir. Bu noktadan sonra sistemin sıcaklığı düşer ve sıcaklık
hedeflenen referans sıcaklığının altına düşer düşmez kontrolör tekrar aktif hale geçer. Görüldüğü gibi bu
kontrolörün genliği üzerinde herhangi bir sınırlama olmadığından çok küçük e değerlerinden de sisteme
maksimum enerji verir.
ON/OFF kontrol karakteristiği.
Sistemin çıkışı referans işaretini aştıktan sonra bang-bang kontrolör maksimum genliğin ters işaretini
uygulayarak çıkışı Yr değerine ulaştırır. Ancak ısıtma işleminde amaç ısıtmadır ve ısıtılmış olan bur sistemi
tekrar kontrolörle aktif olarak soğutmak ekonomik değildir. Bu nedenle kontrolör negatif maksimum genlik
yerine susma (sıfır) pozisyonu alır.
A şağıdaki şekilde açık-kapalı kontrol cihazı ile kontrol edilen bir sistemin sıcaklık-zaman eğrisi görülmektedir.
Açık-kapalı kontrol çıkış eğrisi ve kontrol işareti (ideal)
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 9
Đdeal Açık - Kapalı kontrol transfer eğrisi
Ancak pratikte, endüstriyel sistemlerde bu tip ideal bir on-off kontrol sistemi kullanılmaz. Prosesteki bozucu
faktörler ve elektriksel gürültü nedeniyle, set değeri geçişleri bu şekilde tek noktada olacak olursa sistem
osülasyona geçer ve devamlı set değeri etrafında sık aralıklı açma kapama yapar. Özellikle bu durum son
kontrol elemanlarının çok kısa sürede tahrip olmasına sebep olur. Bu durumu önlemek için set değeri
Geçişlerinde "histerisiz" ya da sabit band oluşturulur.
On-Off kontrolor histeresiz eğrisi
Bu eğriden de anlaşılacağı üzere sıcaklık yükselirken, set değerini geçtiği anda enerji kesilmez, belli bir değer
kadar Yükselir ve o sabit değerden sonra kapanır. Sıcaklık düşmeye
Başlar, set değerine geldiği anda enerji açılmaz, set değerinin Etrafında sabit bir sıcaklık bandı vardır. Bu bandın
genişliği ya da darlığı tamamen prosesin gerektirdiği kadar olmalıdır.
Histerisizli açık-kapalı kontrol formu transfer eğrisi
Đki pozisyonlu kontrolörler
Basit kontrol sistemlerinde PID’ nin yerine iki pozisyonlu kontrolörlerin kullanıldığını görebilirsiniz. Bu
kontrolörle sadece iki kontrol çıkışı üretirler. Bu çıkışlar sadece çalış ve dur manasında On ve Off bilgisidir.
Dolayısı ile bu tip kontrolörler sıcaklık kontrolü gibi hassasiyet gerekmeyen sistemlerde kullanılabilir. Yanda
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 9
görüldüğü gibi sıcaklık belli bir değerin üstünde ise ısıtıcı çalıştırılmaz (Off), değilse o sıcaklığa gelene kadar
çalıştırılır (On).
Rattling (Dalgalanma) Problemi
Rattling problemi iki pozisyonlu kontrolde karşımıza çıkan en büyük dezavantajdır. Bu problem yandaki
şekilden de görüleceği gibi referans değerine ulaşan sistem çıkışında sürekli bir ON-OFF olması ve bunun
sistemdeki mekanik kısma zarar vermesidir. Bunu
örneklemek gerekirse oda sıcaklığı istenen değere geldikten sonra on-off kontrolde ısıtıcı sürekli açılıp kapatılır
ve belli bir süre sonra ısıtıcının çok sık arızalandığına şahit olursunuz.
Histerezis ile On-Off kontrol
Đki pozisyonlu kontrolde rattling probleminin etkisini azaltmak için fark boşluğu kullanılır buna histerezis
denir.Histersiz referans değeri aşılır aşılmaz OFF durumu hemen gerçekleşmez ancak referans değerinin
üzerindeki önceden belirlenen bir değeri aşarsa OFF
durumu gerçekleşir. Aynı şekilde sistem çıkışı referans değerinin altına düşer düşmez ON konumu geçilmez ve
yine önceden belirlenen bir değerin de altına inmesi gerekir. Dolayısı ile ON ve OFF durumları geciktirilmiş ve
mekanik sistemi çok sık ON-OFF olması engellenmiştir.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 9
Histerezis Etkisi
Anahtarlama oranı direk olarak histerezis Xsd den etkilenir. Histerezis arttıkça anahtarlama oranı düşer ancak bu
sistem çıkışında osilasyon artışına neden olur. Dolayısıyla histerezis seçimi problemden probleme değişir ve
kontrol edilen sistemin tipi önemlidir.
Çok hassas olmayan endüstriyel uygulamalarda yapısının basit, fiyatının ucuz olması nedeniyle on/off
kontrolörler tercih edilmektedir. Bunlara örnek olarak termostatlı yapılar verilebilir.
Özetle on/off kontrolörün çalışması aşağıda anlatılmıştır. Hemen altta bir on/off histeresiz eğrisi görülmektedir.
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 9
Hata, +∆e’de çok çok büyük olduğunda ON konumuna geçer.
Hata değeri +.e’ye gelene kadar OFF konumunu, -.e değerine gelene kadar ise ON konumunu korur.
Bu kontrolörde mutlaka bir histerezis bölgesi oluşturulmalıdır. Oluºturulmazsa sistem sürekli
devreye girip çıkar. Histerezisin band genişliği küçüldükçe elemanın devreye giriş-çıkış sayısı artar.
Sistemlerin ataleti nedeniyle kontrol gücü kesildiği halde, ölçülen değer yükselmeye devam eder ve set değeri
üzerinde sürekli bir dalgalanma oluşur. Dalgalanmanın tepeden tepeye değişim ve sıklığı kontrol edilen işlemin
dinamiğine bağlıdır. On-Off kontrol sistemlerinde genellikle anlattığımız sistemin, histeresiz eklenmiş tipi
kullanılmaktadır. Set değeri etrafında histeresiz bandı oluşturulur, proses değeri, set değerini geçer geçmez
kontrol cihazı çıkışı “Kapalı” sinyali üretmez, ancak bu band aşıldıktan sonra çıkış kapatılır. Aynı şekilde,
ölçülen değer histeresis bandının dışına çıkınca “Açık” sinyali üretir.Sistemlerin ataleti nedeniyle kontrol gücü
kesildiği halde, ölçülen değer yükselmeye devam eder ve set değeri üzerinde sürekli bir dalgalanma oluşur.
Dalgalanmanın tepeden tepeye değişim ve sıklığı kontrol edilen işlemin dinamiğine bağlıdır. On-Off kontrol
sistemlerinde genellikle anlattığımız sistemin, histeresiz eklenmiş tipi kullanılmaktadır. Set değeri etrafında
histeresiz bandı oluşturulur, proses değeri, set değerini geçer geçmez kontrol cihazı çıkışı “Kapalı” sinyali
üretmez, ancak bu band aşıldıktan sonra çıkış kapatılır. Aynı şekilde, ölçülen değer histeresis bandının dışına
çıkınca “Açık” sinyali üretir.
ÖRNEK
1. Elimko 111, 0-400 °C, cihazın sabit bandı % 0.5 üzerinden 2 °C´dir. Cihaz 200 °C´ye set edildiği takdirde,
201 °C´de enerjiyi keser, 199 °C´de enerjiyi verir. Toplam ölü band 2 °C´dir.
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 9
2. Elimko 2111 sayısal göstergeli kontrol cihazı 0-1200 °C ise, sabit bandı %0.5 üzerinden toplam 6 °C´dir.
Cihaz 900 °C´ye set edildiği takdirde 903 °C´de cihazın rölesi konum değiştirir, 897°C´de yine korum değiştirir.
Cihaz toplam 6 °C´lik bir bandta çalışır.
NOT: Bu sabit band elektriksel bir sınırdır. Sisteme bağlı olarak tepeden tepeye değişim değerleri bu sabit band
aralığından yüksek olabilir.
Örnek bir
on/off kontrolöre ait histerisiz şekli aşağıdaki gibi gözlenmiştir.
Burada yukarıdaki devreden hareketle R1=5KΩ ve R2=500Ω olarak alındığında +Vcc=+15V -Vcc=-15V
olarak verilirse ve devrede görüldüğü üzere herhangi bir zener diyot kontrolör çıkışında kullanılmazsa
hesaplamalar aşağıdaki gibi olacaktır.
Bu örneğimizde beta değerimiz R2/(R1+R2) formülünden 0.0909 çıkmaktadır. Histerisiz bandının delta e
değeri ise; beta değerinin Vcc değeri ile çarpılmasından 1.363V çıkmaktadır. Vx gerilimi sıfır olduğundan delta
e simetriktir. Vx değerinin değiştirilmesi ile histerisiz bandı pozitif yada negatif bölgede kaydırılabilir. R2 yada
R1 dirençleri ile ise histerisiz band genişliği ayarlanabilir.
Vx değeri özetle hesaplayalım: Vx= R2 / (R1+R2) *Vcc bağıntısından ;
Vx =500/(5000+500)*15
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 9
Vx=1,36V olarak hesaplanır.
Matlab/Simulink ortamında on/off kontrolör aağıdaki gibi gerçekleştirilebilir.
değer histeresis bandının dışına çıkınca “Açık” sinyali üretir.
Yukarıdaki modelde Relay elemanı on/off kontrolör işlevini sağlamaktadır. Dört adet parametre
almaktadır. Umax, Umin, +delta e ve -delta e değerleridir. Bu örneğimizde Umax=1 ve Umin=0 alınmış,
+delta_e= 0.25 ve -delta_e=-0.25 olarak alınmıştır.
Bu sistemde kare dalga kontrolöre ait, üstteki mor sinüs dalga hata sinyali, alttaki sinüs ise sistem
çıkışıdır.
DEĞERLENDĐRME:
Bu deneyde On-Off kontrolörün sürme ya da sürmeme yönlü çalıştığını gözlenmiştir. Burada devrenin
üç temel işleve sahip olduğu birinci bölümde ısıtıcıdan gelen sinyalin verdiğimiz referans girişten çıkarılarak
hatanın elde edildiği yani bir çıkarma ya da hata algılama katı olduğu, ikinci bölümde R1 ve R2 dirençleriyle
histeresis bant genişliğinin ayarlanmak suretiyle Vx geriliminin + ya da – yönde değişerek histeresiz bandını
kaydırabileceği görülmüştür, yani bu bölüm devremizde histeresiz katını oluşturmaktadır. Üçüncü bölümde ise
hataya göre On-Off kontrolörün çıkışında evirici eleman olarak ve OPAMP açık çevrim çalışmakta ve doyumda
olarak kontrolörün çıkışı zener diyot çıkışta bulunmadığı için ya +15 V doyumda ya da -15 V doyumda olacağı
görülmüştür. Eğer on/off tan istenilen tek yönde sürme ise bu takdirde kontrolör çıkışına bir zener diyot
bağlanır. Zener iletimde iken çıkış zener gerilimine eşit olacak, doğru polarma altında ise yapısına göre 0.3 V
(germanyum için) ya da 0.7 V (silisyum için) gerilim seviyesi görülecektir. Böylelikle +15 V doyumdaki çıkış
ters polarmalı bir zener ile transistör elemanını ürdüğünde uygun bir beyz ön direnci ile sadece bir yönde
anahtarı tetikleyecek ve diğer yönde transistöre bağlı röle enerjilenmeyecek ve çıkış yükü kapalı (enerjisiz)
olacaktır. Bu durum devre şeması üzerinden de takip edilebilir.
Çok hassas endüstriyel uygulamalarda yapısının basit,fiyatının ucuz olması nedeniyle tercih edilen bir
kontrolördür.Bu tip kontrolörlere örnek olarak termostatlar verilebilir.
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 9 / 9
Op-Amp'ın giriş gerilimi arttırıldığında belli bir değeri geçtiğinde çıkış değeri maksimum değerine fırlar,giriş
fark gerilimi azaltılırsa belli bir değerin altına inince çıkış max seviyesine iner.
Bu kontrolörde max bir histeresis bölgesi oluşturulmalıdır.Olmazsa sürekli devreye girip çıkabilir. Histeresizin
değei küçültüldüğünde devreye girip çıkma sayısı artar. Bu da mekanik yağıda olan motor elemanlarında kısa
sürede bakım masrafı demektir.
Devredeki Vx gerilimi direk olarak delta e değerini göstermektedir ve bu değer R1 potu yardımıyla
değiştirilebilmektedir. Bir göstergeden buradaki gerilimin dereceye dönüştürülerek gösterilmesiyle dış dünyadan
kullanıcı çok rahatlıkla on/off kontrolörün delta e değerleri dolayısıyla da histeresizin sınırlarını ve kontrolörün
bant genişliğini ayarlayabilir.
ON-OFF kontrolör, kontrol edilen değişkenin çok hızlı değişmediği durumlarda tercih edilir. Çıkış sinyalinin
değişim aralığı azaldıkça kontrolör devreye daha fazla müdahale ederek devreye çok sık girip çıkıyor. Bu da
kontrolörün fazla çalışmasına ve arızalanmasına yol açacaktır. Histeresiz bandının çok iyi seçilerek kontrolörün
devreye en az müdahale etmesini sağlanmalıdır.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk
FastQuiz Exam System
Web MWS System
Web Project System
ACSES System
Proje Seçimi Kura Sistemi
9
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_01/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:9;<=8><:?@<;A@;B@C
DEFEGCHIJKJCLMFJNJOCPQPRSTUVWXYZW[\Z[]ZU
DEFEGCFMCOC^_`_CC
DEFEGCLMFJNJCOCMabMccCd9ef>ghgiC>jklmjnomC
DEFEGCpqprsOCC
`tUSuvSwwUxyz{V|}|~U
||U
tU||
U
^tU|zU
tUW{W
}||||}
U
tUW{W
z|||z||U
tUW{W|z||U
tUPRP U¡||W{W
¢U£¤¥U¦u¦¤£§Ü¦©¦ª£¤«¥¬­U
DEFEGCE®EqpF®pIsOCC
¯|°±²W³y´³µ±|¯¯V¶µ·|²V¶µ²|²¸V¶}|µ²|²¸¸
V¶}|Ux¯||||¹~UU
ºU»¥¨¦U¤¦«ª¦U£¤¥UQ¼U»¥¨¦U½¼U||||¾||¿U
||À²|X³X|
xÁ²¸°µÁ²¸ÂµÁ¯¸°|ï·°¹~µ²|²¸¸U¶µ²
|²¯Ä
µÅU¦Æ¥ÇUµÅU¦Æ¥ÇU³Y²¸¸|¹|¾µ²|z
||}|ÈU
FMÉOC||
x|~³ÊÃU|||¾
|U||­UW³y´³||||||
|Ë|||||¹zU
ÌB:BÍ89ÎÏ>;9Ð9ÑÏÒ8C
ÓUÆ¥u¥¨U£¤¥U¹|¹zÔ|||¹||
Õ|yÁ¡]¡Ô|||||ÖÇÇ©×vvØØØ­ÙÚuÇ¢Ú¤ØÚ¢¤Æ­Ç¬vU
Ø¥ªU¦Æ¢¥Û£u£U§£̈¦¢¥ÇU¥Æ¥ª£¤£¢Û£u£§­UU
DEFEGCÑÜÐÝ;9ÑÍ<:JOCC
zÔ|||¹||Õ|yÁ¡]¡Ô
|||||zÖÇÇ©×vvØØØ­ÙÚuÇ¢Ú¤ØÚ¢¤Æ­Ç¬vUØ¥ªU¦Æ¢¥Û£u£U§£̈¦¢¥ÇU¥Æ¥ª£¤£¢Û£u£§­UU
DEFEGCpDsq®pIsOCC
`tUVz¹¹
|Ë|zU
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
675895:;<=>?@A;BC<DCEFGFHIJHKLHMNGOPOGQHRSTHUHJVWHXYZFHYJHKLZQHRPQME[VH\]^F_FGF̀[H5
a75SbcH\F_FdFG]H_]e]_QGEHMQfGQghGiQGHjHSWHSEbH\F_FdFG]H_]e]_QGEHbN^OHFk]HlHSHOf\OkQfhGh̀[H5
m75]R^VZfFHc]HOR^VZfFHnkoP]MHFoFGHNEFkQEMNbHb_NpkQ_hGhHd]MFki]H\nE^]_Fk]GHGNM^QkQ_QHpQgkQfhGh̀[H5
q75r?@s=?t;uv5wxyHPNiOGQHRz{HPNiOGQVHQkhGh̀Hc]HY[HMQGQkhH|}}HfQbhGh̀[H5
~75SbcH\F_FdHi]g]_FGFHi]gFd^F_FGF̀WH]M_QGiQH||}}HMNG^_Nkn_GHFE^]_]EF̀Hd]MkFGFH]ki]H]iF>@5
]ki]H]^^FgFGF̀H]M_QGH\n_G^EHMQfi]iFGF̀HRoF̀FGF̀VHc]HENGOokQ_hGh̀hH^]N_FMHpFk\Ff]HiQfQGQ_QMH
fN_OPkQfhGh̀[H5
75XYHi]g]_FGFHi]gFd^F_]_]MHFE^]_]EF̀HpQG^H\]GFdkFgFGFHi]gFd^F_FGF̀[H]_QG\FHpF_HpQG^H\]GFdkFgFH
i]g]_FGFH]EQbHfNkOfkQHpOkiOgOGO`Hi]g]_k]_k]5MQ_dhkQd^h_hGh̀Hc]HENGOokQ_hGh̀hHfN_OPkQfhGh̀[H5
75{]kkFHpF_HSEbHi]g]_FHFoFGHFE^]_]EF̀HpQG^H\]GFdkFgFGFH]GHeQ`kQHMQoHSNk^HfQbQpFk]]gFGF̀FH^]EbF^H
C@>@55
75STH\F_FdFGFGHi]g]_FGFHx5c]HHfnGi]Hi]gFd^F_]_]MH]^MFEFGFHp]kF_^FGF̀Hc]HENGOokQ_hGh̀hH
fN_OPkQfhGh55
75K]EFMHoF̀\FHFk]H\nE^]_Fk]GHMhEPhHi]c_]f]HFkQc]H]i]_]MHMNG^_NkHFdk]PFGFH\]_o]Mk]d^F_FGF̀[H
FPkQEfNGHN_^QPhGiQHpOHiO_OPOHFoFGH]_QG\FHpF_HPNi]kHR^_QGEe]_HeNGMEFfNGOWHiO_OPHO`QfhH
c]fQHEheh_xtv<v:xMQ`QGoH\FpFVHE]oFbWHbQ_QP]^_]k]_FGFHi]gFd^F_]_]MH\]_o]Mk]d^F_]pFkF_EFGF̀[H5
75{]kkFH`QPQGHQ_QkhMkQ_hGiQHOR^VWH]R^VHc]HR^VZGFGHi]g]_k]_FGFHMQfi]iFGF̀Hc]H`QPQGQH\n_]H
i]gFdFPk]_FGFHMQfi]iFGF̀[HkihghGh̀HENGOokQ_hHfN_OPkQfhGh̀[5
/ / / / / / / / / / / / / / / / / / / /
0123420
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / / /
6
789:;<96=>?@?ABCDEFG66
H
@8IG6JKLMNOLPQRSTUVWVRXSXQRYZZ[\]]^^^_`KQZLKN^KLNa_Zb]RH^cdRdOeNOQZPfPQaOQRghJiJR
jkjlmnkomHpklHqrHsmomtkoHuvcQcwRxwyMNOWOfPuRdTNVWVQVRbMNNOQOLObRwOLaPWRONOdXNXLzRacQcwR
YObbPQaOROwLPQZPNPRZcKLXbRdXNyXRXSXQRacRwXQcROwQPRfXfZcWXQRdMRacQcwcROXZRZcKLXbRdXNyXRdTNVWVQsmoH
tp{p{|popqk|k{jkok}~HH
H
76E66BHOWOQRfOdXZXR
RfQRcRJZOZXbRbOUOQSRacecLXRKNOQRdXLRUOWOQRfOdXZXRZkkosmkH
fXfZcWXQRZLOQfcLRKQbfXwKQMQMRSPbOLPQPU_RH
6
H
7666BHHKLZOWPQaORdMNaMeMQMURWKacNXRZLOQfcLRKQbfXwKQMRZVLVQacRKNMZMLMQMU_R
O[PNOQRXNcWROaPWNOLPQPROSPbNOwPQPU_H
6
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
6789:;:<:=>5?@ABC@DEFGHIJAKDLJFM@MINA@D@O@FEJPJCKFQNRH@AFGCJHJEFENDL@FSONH@DLNDFTNH@F
UNMCNANC@FEGDIHGCVHMSOFGCJHJEFLBHBAFBOJWKFISHSDLNFAGLNCCNW@D@OXF?@MINAFYNRJUKDKF
TVOCNACNW@D@OXF?GDBQCJHKDKOKFWGHBACJWKDKOXF5
Z[\]^_:̀
5
6789:a:<:=>5bBFM@MINANFcNCJWFUCGdBFNECNWNHNEFe@MINHNM@OFUJDLKfgFhFRNFEGDIHGCVHFQKEKiKFj
klmnklFhFJHJMKDLJFGCAJEFSONHNFM@MINA@DFLNDNI@A@D@FTNHQNECNiI@H@D@OXF?@MINAFQKEKiKDKF
TVOCNACNWNHNEFJCLKdKDKOFMGDBQCJHKFWGHBACJWKDKOXF5
Z[\]^_:̀
5
6789:o:<:=>5p@O@EMNCFGCJHJEFLNRHNLNFM@C@MWBAFWJPKLJE@FU@HFONDNHFL@WGIFUJdCJDAJMKFLBHBABDLJF
?@ABC@DEFGHIJAKDLJE@FEJPJCK5QNRH@AFM@MINAF@Q@DFTNHNEC@FLNd@i@EC@ECNH@FWJPJHJEFM@MINA@DF
LNDNI@A@D@FTNHQNECNiI@H@D@OXF?@MINAFQKEKiKDKFTVOCNACNWNHNEFJCLKdKDKOFMGDBQCJHKFWGHBACJWKDKOXF5
Z[\]^_:̀
5
6789:=:<:=>5bBFLNRHNFeJEEKDLJFq5rJHECKFMGHBFeJOKHCJWKDKOFs?GHBCJHFOGHFD@INC@EINFGCAJCKLKHFRNF
QVOSASDSFeJOKHCJAJWJFTNHNEFWGEIBHXF?GHBCJHFWBEJHKLJE@CNHLNDFrJHECKFGCJYJEIKHXFbJM@IFMGtuvwt5
LNdNHCNDL@HANWNFJCKDAJWJYJEIKHXx5
Z[\]^_:̀
5
5
5
0112340
TEORĐK BĐLGĐ
Sayfa 1 / 12
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-3.2):
Orantı etkiye integral etki ilavesi veya PID denetiminde D türev etkinin devre dışı bırakılmasıyla elde
edilen PI tipi denetim organı yapısı nispeten basit olup endüstriyel uygulamaların %90’ında PI
denetim kullanılmaktadır. Đntegral etki biriktirilmiş hataya orantılı bir denetim çıkışı oluşturarak
hatanın zaman içinde sıfırlanmasını sağlar. Bu integral etkinin olumlu tarafıdır. Diğer taraftan integral
etki hatayı biriktirerek düzelttiği için denetim etkisi ve hatayı düzeltmesi zaman alır.Bu da integral
etkiyi yavaş tepkili denetim biçimi yapar ve integral etkinin olumsuz yönüdür.Ayrıca integral etkiden
dolayı paydaya katılan bir s çarpanı integral etkili denetime 90 derecelik faz gecikmesi verir ki bu
geribeslemeli sistemin kararlılığını kötüleştirir.
Đntegral etkinin kullanım amacı sistemin değişen talepleri üzerinde yeterli bir denetim etkisi
sağlamaktır. Eğer sistemden gelen bir talep yalnız başına P etkisi ile karşılanabiliyorsa I etkinin
kullanılması gereksizdir. Örneğin bir sıcak su elde etme sisteminde belli aralıklarla çekilen sıcak suya
karşılık kazana dolan soğuk suyun ısı enerjisi talebi çok fazla değilse ve bu talep de çok sık aralıklarla
değişmiyorsa orantı etki tek başına yeterli olabilir. Buna karşılık sistemden oldukça sık aralıklarda
yüksek miktarda talepler ortaya çıkıyorsa P etkisi yalnız başına bu talepleri karşılayamaz. Böyle bir
durumda talebin (bozucu giriş)büyüklüğüne bağlı olarak sistemde kalıcı durum hatası ortaya
çıkacaktır. Eğer P etkisine I etkisi ilave edilecek olursa denetleyici çıkışından sürekli artan (integre
olan) denetim etkisi elde edileceğinden motor elemanının, hatanın ortadan kalkmasını sağlayacak
kadar hareket etmesi temin edilmiş olur. Bu işlem sonucu denetlenen çıkış büyüklüğünde ortaya çıkan
sapma sapma sıfırlanmış olur.
Standart PI denetiminin transfer fonksiyonu ise aşağıdaki şekildedir;
Buna göre PI denetleyicisi tüm ileri yol transfer fonksiyonunu Tip1 haline getirir. Bu da teorik
olarak I etkinin kalıcı durum hatasını nasıl giderdiğini gösterir.
Oransal kontrolda oluşan off-set, manuel veya otomatik olarak kaldırılabilir. Otomatik resetleme için
kontrol cihazı, elektronik integratör devresi kullanılır. Ölçülen değer ile set edilen değer arasında fark
sinyalinin zamana göre integrali alınır. Bu integral Değeri, fark değeri ile toplanır ve oransal bana
kaydırılmış olur.Bu şekilde sisteme verilen enerji otomatik olarak artırılır veya Azaltılır ve süreç
sıcaklığı set değerine oturtulur. Đntegratör Devresi gerekli enerji değişikliğinde set değeri ile ölçülen
değer Arasındaki fark kalmayıncaya kadar devam eder. Fark sinyali sıfır Olduğu anda artık integratör
devresinin entegralini alacağı bir Sinyal söz konusu de¤ildir. Herhangi bir şekilde bazı değişiklikler
Olup, sıcaklık değerinden uzaklaşacak olursa tekrar fark sinyali oluşur ve integratör devresi düzeltici
etkiyi gösterir. Şekilde oransal+entegral kontrol formu blok şema halinde verilmektedir. Ayrıca ofseti kalkmış reaksiyon eğrisi de verilmektedir. Oransal+integral kontrolün en belirgin özelliği sistemin
sıcaklığı ilk başlatmada set değerini geçer, önemli bir miktar yükselmeyapar (overshoot). Set değeri
etrafında bir-iki salınım yaptıktan sonra set değerine oturur.
Oransal+integral kontrolor blok şeması aşağıdaki biçimdedir.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 12
Kontrol edici çıkışı, hem dinamik hata ile hem de dinamik hatanın zaman integrali ile doğru
orantılı olarak elde edilir. matematiksel olarak (p+ı) denklemlerinin toplanmasıyla elde edilen kontrol
edicidir. oransal+integral kontrolün en belirgin özelliği sistemin sıcaklığının ilk başlatmada set
değerini geçmesi ve önemli bir miktar yükselme yapması (overshoot), bu yükselme sonunda set
değeri etrafında bir-iki salınım yaptıktan sonra set değerine oturmasıdır. sürekli tip uzun süreli fırın ya
da proseslerde ve off-set arzu edilmeyen hallerde pı tip seçilebilir.
Aşağıdaki şekilde PI kontrolör şeması verilmektedir. Sistemde oluşacak hata sinyali
kontrolörde değerlendirilerek çıkışa aktarılmaktadır. Hata sinyali e(t) sistem kazancı ile çarpılmakta
ve hata sinyalinin integrali alınmaktadır. Sistemde integratör kullanılarak çıkıştaki aşım önlenir.
Hata sinyalinin değerine göre PI çıkışı artırır veya azaltır.
PI kontrollü bir sistemin transfer fonksiyonu ;
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 12
G(s)=Kp+
şeklindedir.
(a)
(b)
PI kontrolörünün işlemsel kuvvetlendiricilerle gerçekleştirilmesi
(a)iki işlemsel kuvvetlendiricili devre
(b)üç işlemsel kuvvetlendiricili devre
(a)’daki şekilde iki işlemsel kuvvetlendiricili devrenin transfer fonksiyonu;
G(s)=
şeklindedir.G(s)=Kp+
=
+
denklemi ile karşılaştırılırsa;
Kp=
Ki=
olduğu görülür.
(b)’deki şekilde üç işlemsel kuvvetlendiricili devrenin transfer fonksiyonu;
G(s)=
=
+
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 12
olarak elde edilir. Buna göre PI kontrolör katsayıları devre parametreleri cinsinden ifade edilirse;
Kp=
Ki=
olduğu görülür. Kp ve Ki değerleri bağımsız devre parametrelerine bağlı olduğundan (b)’deki devre
daha üstündür. Ancak her iki devrede Ki katsayıları kapasite değeri ile ters orantılıdır. Ne yazık ki
etkin PI kontrol tasarımında küçük Ki değerlerine ihtiyaç duyulur ve gerçek dışı geniş kapasite
değerleri ile karşı karşıya gelinir.
Olarak bulunur. Bu değer bizim PI tasarımında kullandığımız pay değeridir.
Olur. Bu integral katının mekanik sistemin transfer fonksiyonu ile çarpılması
sonucunda sistemin transfer fonksiyonu ortaya çıkar.
Mekanik bir sistem örneğini ele alalım. Bu sistemin ileri yol kazancı PI kontrolör dahil olarak
şağıdaki gibi verilmiş olsun.
Buradan gerekli düzenlemeler yapıldığında aşağıdaki ifadeyi elde ederiz.
Şimdi böyle bir sistemi Matlab ortamında inceleyelim.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 12
>> m=50;
>> c=50;
>> k=2000;
>> k1=100;
>> k2=10;
>> kp=20;
>> ki=10;
>> pay=[k1*k2*kp,k1*k2*ki];
>> payda=[m,c,(k+k1*k2*kp),k1*k2*ki];
>> step(pay*0.15,payda)
Sistem çıkışına dikkat edilecek olursa sistem cevabının doğrusal olarak gittikçe azalan salınımlardan
oluştuğu görülür. 4. sistemde sisteme bozucu giriş uygulanmamıştır. Yani istenen değerler çıkışta
gözlenir. Bozucu giriş 10 N olduğunda çıkışın yine aynı olduğu gözlenmiştir. O halde sistem 10 N luk
bozucu giriş için istenilen yönde çalışıyordur. Bunu sistem çıkışının sistem çıkışı ile aynı olduğundan
çıkartabiliriz. Sistem çıkışı 10 N yerine 1000 N olarak alınırsa sistemin istediğimiz gibi olmadığı
gözlenir. Sistem salınımları doğrusal değildir ve sistem daha çok negatif değerler alır. Bozucu girişin
etkisinden kurtulmak için Ki ve Kp değerleri yeniden seçilmelidir. Doğru seçilen değerlerle sistem
bozucu girişin etkisinden kurtulabilir.
PI kontrolörün genel ifadesi;
şeklindedir.
Bundan yararlanılarak çeşitli girişlere göre sistem çıkışları belirleyelim.
Öncelikle sistemde bulunan m(kütle), c (söndürücü) ve k (yay sabiti) değerlerimiz belirli bir sabit
değerde olacağından, her örnek için bu değerleri aynı tutacağız.
Sadece Kp ve Kı değerlerini değiştirerek sistem çıkışını gözleyeceğiz.
O halde m = 50 c= 50 ve k= 2000 alınırsa bu sistemin zamana göre yer değişim grafiği şu
şekilde olur.
Ki =50 ve Kp=100 dür.
>> m=50;
>> c=50;
>> k=2000;
>> ki=50;
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 12
>> kp= 100;
>> pay=[kp,ki];
>> payda=[m,c,(k+kp),ki];
>> step(pay,payda)
Sistem çıkış cevabındaki Ki ve Kp değerlerini referans olarak kabul edilirse sistemin
kararlılığa geçtiği sürenin Ki ve Kp değerleri ile ters orantılı olduğu görülür. Sistem çıkış cevabı
yaklaşık olarak 120ms dır. Şimdi bu veriden yola çıkarak Ki ve Kp değerlerini arttırıp arttırmak sureti
ile çıkışın değişimlerini gözleyelim. Bu noktada dikkat edilmesi gereken sistemin kararlılık anı nihai
değerin % 95i olduğu andır.
Ki=25 ve Kp=50 için;
>> m=50;
>> c=50;
>> k=2000;
>> ki=25;
>> kp=50;
>> pay=[kp,ki];
>> payda=[m,c,(k+kp),ki];
>> step(pay,payda)
Sistem çıkış cevabındaki Ki ve Kp değerleri referans değere göre yarı değerine düşürülmüştür. Bunun
sonucunda sistemin kararlılığa geçme süresi grafikten görüldüğü üzere yaklaşık olarak 240 ms dir. Bu
sonuca göre Ki ve Kp değerleri yarı değerine düşürüldüğünde sistem zaman cevabının 2 katı fazla
olduğu görülmektedir.
Ki=100 ve Kp=200 için;
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 12
>> c=50;
>> m=50;
>> k=2000;
>> ki=100;
>> kp=200;
>> pay=[kp,ki];
>> payda=[m,c,(k+kp),ki];
>> step(pay,payda)
Sistem çıkış cevabında ise Ki ve Kp değerleri referans değere göre iki katı değerine çıkarılmıştır.
Bunun sonucunda sistemin kararlılığa geçme süresi grafikten görüldüğü üzere yaklaşık olarak 70 ms
olarak bulunmuştur. Bu sonuca göre Ki ve Kp değerleri iki katı fazla alındığında sistem zaman
cevabının yaklaşık olarak 2 kat daha hızlı olduğu görülür.
Şimdi ki inceleyeceğimiz çıkışta m, c ve k değerlerini farklı bir değerde tutup yine Ki ve Kp
değerlerini değiştirerek sinyal çıkışı gözleyelim.
Bu incelemede m=1 c=10 ve k=20 değerinde sabit tutulur ve Ki ve Kp değerleri:
Ki=50 ve Kp=100 için;
>> m=1;
>> c=10;
>> k=20;
>> ki=50;
>> kp=100;
>> pay=[kp,ki];
>> payda=[m,c,(k+kp),ki];
>> step(pay,payda)
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 12
Bu üç çıkışa dikkat edildiğinde Ki ve Kp değerleri büyüdükçe aşım miktarının da büyüdüğü
görülmektedir. Đlk Ki ve Kp bizim ele aldığımız referans değerimiz olun ve diğer çıkışları bu değere
göre yorumlayalım. 10. sistem çıkış cevabında aşım miktarının 0,05 m olduğu gözlemlenir.
En son olarakta m,c, ve k değerlerini arttırarak sistem cevabını yeniden değerlendirelim. Ki ve Kp
değerlerini aynı kullanacağız. Ve tekrar üç tane çıkış eğrisi elde edeceğiz.En son örnekte m=1000
c=10000 k=20000 olarak alalım;
Ki=50 ve Kp=100 için;
>> m=1000;
>> c=10000;
>> k=20000;
>> ki=50;
>> kp=100;
>> pay=[kp,ki];
>> payda=[m,c,(k+kp),ki];
>> step(pay,payda)
Bu sistem incelenirken dikkat edilmesi gereken nokta, sistemin büyük bir sistem olduğudur.
Tabi doğal olarak sistem cevapları da bir o kadar geç olacaktır.
Şimdi MATLAB/Simulink ortamında adım adım bir PI kontrolörlü sistem tasarımı nasıl yapıldığına
göz atalım.
1.
olan sistem MATLAB da kurularak önce kontrolörsüz ve kapalı çevrim olarak
çalıştırılmış olsun. Buradaki sistem 1.5 sn lik bir zaman sabitine sahip birinci mertebeden bir sistem
olmasına rağmen kapalı çevrim çalışmada çok fazla kalıcı hal hatası (yaklaşık 0.3 birim kadarlık bir
hata) olduğundan dolayı PI kontrolör ile denetlenmek istensin. Sistemin kendi üzerinden kapaılı
çevrim çalışması aşağıdaki gibidir.
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 9 / 12
2. Sistem cevabında oluşan kalıcı hal hatasını gidermek amacıyla sisteme integral kontrolör
eklenmiştir ve sistemin cevabındaki iyileşme grafikte görülmektedir. .
9
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 10 / 12
3. Sistemin cevabında aşım görülmektedir. Sistemde integratör kontrolör olduğu için bu aşımı
gidermek amacıyla Kp arttırılarak sistem cevabı tekrar gözlemlendiğinde sistem cevabının referansa
oturduğu görülmektedir.
10
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 11 / 12
DEĞERLENDĐRME:
PI kontrolör tasarlanırken öncelikle kullanılacak sistem belirlenmelidir. Uygun yaklaşımda
bulunmak için uygun değerler seçilmelidir. Büyük sistemlerde büyük Ki ve Kp, küçük sistemlerde
küçük Ki ve Kp seçilmelidir.
Kp ve Ki seçilirken transfer fonksiyonuna önem verilmelidir. Yani tasarlanacak sisteme göre
Ki ve Kp sabitleri koyulmalıdır.
11
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 12 / 12
Kp(Oransal Kontrolör katsayısı) değeri arttırıldığında yükselme zamanı kısalır, max aşım
artar, oturma zamanı kısalır ve kalıcı hal hatası küçülür. Kp değerinin asıl etkisi yükselme zamanı
üzerindedir.Ki değeri arttıkça yükselme zamanı kısalır, max aşım artar, oturma zamanı artar, kalıcı hal
hatası ise sıfırlanır. Ki (integral kontrolör katsayısı) etkisi kalıcı hal hatası üzerinde
yoğunlaşır.Sisteme orijinde kök ekleyerek kalıcı hal hatasını sıfırlar.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
12
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_02/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDCEFGHIFDJKFELKEMKN
67879:8@:B:OPQP::
67879:?@8=A=:B:RSTUVWXYVZ[Y:
67879:\]\^_B::
`aNbcHdefgheijhkHglfmnldoN
QaNIlimpmHqliHqlglrmsHgtghuvtnititdHwuHlvmnHxtytHdlwhlnilhmfHrtrgunHkzuhtf{udtHugdtiuhtftH
j|hufnudoHN
OaNbHwuHcHdefgheijhiuhtfHl}hmHl}hmHugdtiuhtftfHfuiuhHei{~|~f~HytiuytinudoHN
aNthHbcHdefgheijhHlhlnughuiuhtftfHrtrgunHkzuhtf{uHflrmiHugdtH}lgm|mfmHj|hufnudoN
aNbcHghlfruhHu|htrtftHmdlhlytinudoHN
aNNwuHtn~itfdHehglnmf{lHbcHdefgheijhHtiuHlflitzH}llytinudoN
67879:77]\8\<_B::
NNNNHl{ugHHIHeglfrt}enughusHHl{ugHHIsHHl{ugHHNNN
HruhweHnegehHrtrguntH¡lixmil}mpmHuiunlfmHtiuHgkniuvtdHeilhld¢oN
8£¤BN¥rguftithruHbcNdlgmHttfHbcHne{kikHd~iilfmilytithoH~Hvudti{uHFbC¦bHuiunlfmfmHwuH
{t|uhHuiunlfilhmHd~iilfnl{lfH{lqlHdeil}HwuHylrtgHythHvudti{uH{uwhuHglrlhmnmH
xuhudiuvgthtiuytithoHN
§¨©¨ªT«¬SU­«®«¯S°T:
~H{ufu}HtiuHtixtitHguehtdHwuHl}hmfgmimHytixtiuhHttfH±uyHglylfimHrtnkilr}efH~}x~ilnlrmH
tnd²fmHr~flfHC MHrtrguntH±uyHyl|ilfgmrmflH~ilvnldHkzuhuH³´µ¶¶···¹̧º»¼º½·º¼½¸¾¶N
·¿N¼ÀÁ»ÁNÂÁüN¿Á½Á¼ÀÁ»ÁÂŅN
67879:̄Įŭ«¯ªÆ©ÇB::
~H{ufu}HttfH±uyHglylfimHrtnkilr}efH~}x~ilnlrmHtnd²fmHr~flfHC MHrtrguntH±uyH
yl|ilfgmrmflH~ilvnldHttfH³´µ¶¶···¹̧º»¼º½·º¼½¸¾¶N·¿N¼ÀÁ»ÁNÂÁüN¿Á½Á¼ÀÁ»ÁÂŅN
67879:\6_]\<_B::
`aNÈudti{udtH{uwhu}tHd~h~f~zoHlvilfxmglHbsHcHwuHCHlflqglhilhmfmfHlmdHei{~|~f{lfHuntfH
º½É»ÉÂŅN
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
5
5
5
67589:;<=>?>@>A8<B>ACDE<F8A8?D:G?HAI8A<J5KLE:<:8M8<I8N8?>A8<BDO>M<J5PQR<S?8TDABUAID<V>?<TD?8<
IDE=D<>@D?8:><WC=WEDCUAURX<5
Y75Z<DADO:D?UAU<TDMD:UAURX<[LA:?LEG?HA<L?DABDE<8E8\DAUAUA<9Z<8E8\DAU;<]UTU@U<:8L?>T<LED?DT<A8<
:H?<V>?<IDE=D<LE\DEUIU?^<_B>ÈBTLM:D<W9:;<]UTU@UAU<:8L?>T<BLAW]ED?UAURD<IDCDAD?DT<=GRE8C>M<
]>R>A>RX<_?DABDE<TLA:?LE<I8a?8B>A>A<TDRDAbUAU<CL?W\EDCUAURX<89:;<=>?>@8<B>AHBc<H]=8A<:>M>AI8<
SD?TEU<>@D?8:E8?<WC=WEDCUMc<BLAW]ED?UAURU<TDCI8I>A>RX<de<ML:WAWA<SD?EU<I8N8?E8?><>]>A<DEIUNUAUR<
BLAW]ED?U<a8<]UTU@<>@D?8:>A><CL?W\EDCUAURX<5
f75gX<DIU\U<WC=WEDCUMc<IDOD<BLA?D<Z5`h`ij̀?U<TDMDEU<>T8A<k<DADO:D?UAU<TDMD:UAURX<[LA:?LEG?HA<
lm`hn`op>A:8=?DE<8E8\DAUAUA<9k<8E8\DAU;<]UTU@U<:8L?>T<LED?DT<A8<:H?<V>?<IDE=D<LE\DEUIU?^<
qnròBTLM:D<W9:;<]UTU@UAU<Zk<:>M><V>?<TLA:?LEG?HA<]UTU@UAID<V8TE8A>E8A<:8L?>T<BLAW]ED?UAD<
IDCDAD?DT<=GRE8C>M<]>R>A>RX<sN8?<>@E8\><VD@:DA<CDM\DT<>B:8?B8A>R<GAb8E>TE8<t<DADO:D?UAU<
0123240
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67889:9;96<=><6?:@9:A9BC;D:D<@EF9;G<E@>:>HI<J>K<L?B7:7:<M9;8N<@EOE;8E;><>P>:<98@NON:NH<
A?:7P89;N<QE<PN6NF<>F9;EB>:><R?;7S89RN:NHI<T
UVTW:XE6><Y<S9@@E@E<9R;N<9R;N<ZCABE;>8SEA><ZE;E6E:<BE?;>6<PN6NFTZ;9M>68E;>:>[<\]<6?:B;?8C;D:<
PN6NFN:@9<BE?;>6<?89;96<:9AN8<ZCH8ESE:>H<ZE;E6B>O>:><P>H>:>HI<^A>89A6?LB9<E8@E<EBB>O>:>H<PN6NF<
Z;9M>O>R8E[<BE?;>6<?89;96<_E68E@>O>:>H<Z;9M>O><69;FN89FBN;N:NHI<`D;D8BD<?8S9AN<@7;7S7:@9<?;9:A98<
abTcdebfghiTebgcjibgcdkbdTlhdfcmcd>:<A>ABES><E:<P?6<EB6>8EREXEO><n966N:@9<R?;7S89;N:NHN<
R9HN:NHIT
o
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
pqrsturovwxyxzV{|}~oo
T
yqo?;789;N:<PCHDSD<>P>:<nBBLIX?:B;?8?;8@IB6<TE_<_9O89:BNAN:@9:<
=<
mcmebjcdbThceTTkbdbcdTE:ER<RZ789S9AN<_C8DSD:D<67889:9;96<R9;@NS<989_>8>;[<@E:ER<
n966N:@9<9R;N:BN8N<BE?;>6<_>8Z><>P>:<@E<R>:E<9R:N<A>ABES>:<_7<@E:ERE<9>B<BE?;>6<_>8Z><_C8DSD:@E:<
hghgihdhcicgmcdcTT
T
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;:<:=>?@ABCDEE?FGHIJ?KL?MLNGBEOPD?QRGA?STF?TUTAVT?WLFNLSLHLA?JTJNLWTA?NFGAJXLF?
YZ[\]^_Z[`[`abc\dec[cfga?
hijklmn:
?
6789:o:<:=>?pqrsqt?Zeudvc[wdax`yw`z`[`favZw{y^aued[]Y{eaYZ[\]^_Z[`au|e|[w{aZỳ}ùe`[`fga
~`avZw{y^awdda]Z[eda]]aw`e`va`fd_ca{af\a]cYceU
N
\dfd[bavZw{yy{e^[{a
w[|}u|e|[|fgadcyd[a^}y{vadwcvydec[cadbc\yd_c[cfg?
hijklmn:
?
6789::<:=>?^v`y^[\aZeudvc[wda]^]u{v^[^f^a\ddycab{e^vaZyded\a\{[w^a|f{e^[w{[a{e^a
x{]y{v{y^a\Z[ueZye]|faZyded\aw`e`va`fd_cau|e|[w{avZw{yy{_^[^fga^]u{va{dxc[ca
fy{vy{_^[^fgaZ[`bydec[cfca_Ze`vyd_c[cfga?
hijklmn:
?
6789::<:=>?~`a]^]u{v{a[{aaZed[]dya\Z[ueZyea\`yyd[ded\aw{[{u^v^[^a_dc[cfga^]uLW?
bc\c}c[cafy{vy{_{e{\adywczc[cfa]Z[`bydeca_Ze`vyd_c[cfga?
hijklmn:
?
6789::<:=>?~`a]^]u{v{awdda]Z[edaa^[u{edya\Z[ueZyea{\y{_^[^fga^]u{vabc\c}c[wd\^a\dycca
dyadud]ca{a]^]u{vw{\^ad}cvav^\udeca{ad}cvafdvd[c[cafy{vy{_^[^fgaywczc[cfa]Z[`bydeca
Qe`vyd_c[cfga?
hijklmn:
?
6789::<:=>?d\]^v`vad}cvaa\dyccadyadud]caa{aZùevdafdvd[caa][aaw{[adfaZyvd\a
|f{e{aa\du]d_cydec[cad_deyd_c[cfga?
hijklmn:
?
6789:=:<:=>?~`aw{e{ad\\c[wda?Yde\yca]Ze`adfceyd_c[cfaZe`ydeafZea[^u{y^\u{aZyvdycwcea{a
bf|v|[|adfceydvd_da{e{\a_Z\ùegaZe`ydea_`\decwd\^y{ew{[aYde\ycaZydd\ucega~d]^ua]Ze`ydea
w{z{ey{[w^ev{_{adyc[vd_dd\uceg?
hijklmn:
?
?
?
0123450
TEORĐK BĐLGĐ
Sayfa 1 / 14
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY-3.3):
C
Celsius (sıcaklık birimi)
offset
kayma (sıfır hatası)
CO denetimci çıkışı
P
oransal mod
D
türev modu
PID
oransal-integral-türev modu
I
integral modu
PV
proses değeri (mevcut ölçüm)
Kd türev kazancı katsayısı
PV - SP hata
Ki integral kazancı katsayısı
SP
set değeri (prosesteki hedef
ölçüm)
Kp oransal (orantı) katsayısı
Modern proses kontrolü nispeten yeni bir alandır. Tüm proses endüstrilerinde denetimciler yaygın
olarak kullanılmaktadır. PID (Proportional-Integral-Derivative) günümüzde çok kullanılan bir kontrol
yöntemidir. Kullanıma hazır oransal-integral-türev (PID) algoritmasını kullanan sürekli geri-beslemeli
proses denetimcileri, ancak 1940'lardan beridir ortalarda.
Bu kontrol teorisinin matematiksel altyapısını 1800'lerin sonlarında Fourier, Laplace, Kirchoff,
Kelvin ve diğerleri oluşturdular. Tüm terimler, yani orantı, integral ve türev, belli aritmetik
manipülasyonlara atıfta bulunuyorlar. Son ikisi calculus (değişkenler hesabı) için kalbi oluştururlar.
PID kontrol teorisini anlamak için matematiksel karmaşıklığın araştırılması şart değildir. Grafiksel bir
kavrayış ve teknik bir yorumlama yeterli olacaktır.
Herhangi bir sistemin kontrolü
Öncelikle kontrol edilecek bir parametre düşünelim. Soğuk suyla beslenen ve sürekli 100°C'de su
pompalayan bir depodaki suyun sıcaklığını alalım. Buradaki proses şudur: Eğer gelen su 100°C'nin
altındaysa, sıcaklık istenen değere yükselene kadar değişken bir gaz alevi uygulanması.
Bu proseste kontrol edilen parametre ise sıcaklık. Set değeri (SP) 100°C. Set değeri ile mevcut
sıcaklık değeri (PV) farkına hata (sapma) veya kayma (offset) denir. Bir hata oluştuğunda denetimci,
ısı verilmesi için sinyal (CO) gönderir.
1
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 2 / 14
En başta Oran(tı)sal
Oransal mod (P) üç kontrol modu içinde en az
karmaşık olanıdır. Matematiksel ifadesi:
CO = Kp (PV - SP)
Kp değerine oransal (orantı) katsayısı denir.
Operatörün prosese müdahale için kullanabildiği,
denetimci cihazın üzerinden girilen ayarlanabilir bir
sayı için biraz fiyakalı bir terimdir.
Örneğin Kp değeri -0,5 , PV değeri 98°C ve SP
değeri 100°C olduğunda, CO değeri 1 çıkar.
Bu 1 değeri deponun altındaki brülöre alevin belli
bir yoğunluğa ayarlanacağını ifade eder.
Şekil 1 - Orantı(sal) kontrol
Aynı şekilde eğer depoya dışarıdan gelen su 100°C
ise, (PV-SP) sıfıra eşit olur, dolayısıyla CO değeri
de sıfır olur, bu da muhtemelen deponun altındaki brülör için alev ayarı sıfır veya hiç alev yok
anlamına gelir.
Oransal modun Kp olarak tek bir ayarı olduğundan,
en kolay kullanılabilendir. Oransal mod hiçbir zaman
set değeri ile gerçek değer arasındaki farkı tamamen
yok edemez (bkz. Şekil 1). Bununla beraber, hızlı
tepki verir ve kararlıdır.
Sonra Đntegral terimi
PID algoritmasının integral terimine yönelik ifadesi,
Isaac Newton tarafından bulunan calculus'den (bir
matematik disiplini) kaynaklanır.
CO = Ki ∑(PV - SP)dt
Bu ifade (PV-SP) hata değerlerinin zamana bağlı
Şekil 2 - Zamana göre hatanın integrali
olarak (dt) toplanıp (∑), Ki ayar faktörü ile çarpılması
ve denetimci çıkış sinyalini gösteren rakamın elde
edilmesini gösterir.
Calculus matematiğinde integral alındığında bir çizginin altında kalan alan bulunur. Zamana karşı
hatayı çizdiğimizde bir doğru elde ederiz (bkz. Şekil 2). Böylece eğer t1 anında hata 2 ise ve t2 anında
hata 3 ise, integral aldığımızda elde edeceğimiz sonuç Şekil 2'deki doğrunun altında kalan taranmış
alan olur.
Benzer şekilde hem t1 hem de t2 anlarında hata sıfırsa,
doğrunun altında kalan alan yok demektir ve yukarıdaki
eşitlikten CO değeri sıfıra eşit olur.
Oransal mod için olduğu gibi ayarlar bir katsayı kullanılarak
yapılır. Ayrıca doğrunun çizildiği zaman periyoduyla
oynanabilir.
2
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 3 / 14
Oransal modun aksine, integral işlemi hatayı tek başına yok
edebilir (bkz. Şekil 3). Ne var ki hatayı yok etmek için uzun
zaman dilimine ihtiyaç duyduğundan, düzeltme yavaş
gerçekleşir ve nispeten küçük sistemlerde kullanışlıdır.
P modu ve I modu eşitlikleri çoğunlukla her iki modun
avantajlarından yararlanmak için birleştirilirler. Đntegral
terimi hatayı bertaraf ederken, oransal terim tepki hızı ve
kararlılık sağlar.
Kontrol için Eğimleri kullanmak
Şekil 3 - Đntegral kontrol
PID kontrol ifadesinin D terimi ''türev'' (derivative)
kelimesine karşılık gelir ve yine calculus'den kaynaklanır.
CO = Kd [d(PV - SP)/dt]
Türev kontrol modu, parametrenin (sıcaklık) mevcut değeri ile set değeri arasındaki farkın (PV-SP)
değişim hızına göre kontrol çıkışı verir.
Bunun görsel izahı daha açıktır. Şekil 2'de
doğruyu çizerken kullanılan aynı veriyle Şekil
4'te özdeş bir doğru gösterilmiştir. Türev
eşitliğinin [d (PV-SP)/dt] kısmı basitçe
hatadaki değişimin zamandaki değişime
oranını ifade eder. Bu örnekte her bir (∆y)
nin, geçen zamana (∆t) bölünmesi anlamına
gelir. Eğer geçen zaman 10s ise sonuç 1/10
olur. Bu sayı daha sonra ayar katsayısı (Kd)
ile çarpılarak CO değeri elde edilir.
Türev modu hiçbir zaman tek başına bir
prosesi kontrol edemez. Bunun bir nedeni set
değerinden sabit bir sapma olması durumunda
yukarıdaki eşitliğin sıfır olmasıdır. Benzer
şekilde proses değişkeninde ani bir değişim
Şekil 4 - Hatanın türevi
olması halinde denetimciye (teoride) sonsuz
bir sinyal gönderilir, bu da ilgili aparatların
tam açık ya da tam kapalı olmasına, bitmeyen bir kararsızlık sürecine sebep olur.
Hemen hemen bütün proses kontrol döngülerinde var olan gecikmeleri karşılamak için, türev işlemi
denetimciye önceden hazırlanma zamanı (avans zaman) verir. Doğru uygulandığında prosesi kararlı
hale getirir.
Boşta gezen sistem PID değil
Üç modun herbirinin temel özelliği aynı giriş verilerine (Kx, SP ve PV) karşılık birer sayı (CO)
üretmeleri ve bu sayının her mod için farklı olmasıdır. Veri girişi ile birlikte bu sayılardaki
oynamalar, PID ilişkisinin büyüsüdür.
3
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 4 / 14
Üç modun özgün rakamları biraraya getirildiğinde bir PID denetimcisi sistemi kontrol eder. Oransal
mod temel kontrolü sağlar. Đntegral mod, oransal modun yetersiz kaldığı uzun dönemli hatalarla
ilgilenir. Türev mod, süregiden proseste ortaya çıkan belirgin bozucu etkilerle ilgilenir.
PID algoritması, sistem büyük olduğunda, bazı proses parametrelerinde ani değişimler olduğunda ve
bu değişimler büyük olduğunda kullanılır. Karmaşık bir sistemdir ve verimli bir şekilde set değerine
ulaşma ve sürdürmeyi garantilemek için her bir modun değişik katsayılarının (Kp, Ki, Kd) başlangıçta
doğru oturtulmasını gerektirir.
Endüstrideki uygulamaların %75’inde uygulanmıştır. Çok geniş bir uygulama alanının olmasına
rağmen PID uygulamaları için standart bir tanımlama yoktur. Karl Astrom'a göre PID algoritması
aşağıdaki gibidir:
Burada u(t) kontrol değişkeni, e(t) toplama noktası, y(t) çıkıştan ölçülen değerle aynıdır. K, Ti, Td
PID parametreleridir. Yukarıdaki formülü biraz daha basite indirgersek:
P: Oransal
I: Đntegral
D:Türevsel
Ancak, değişik kaynaklarda farklı PID algoritmalarına raslamak mümkündür. Bir diğer PID
algoritması da aşağıdaki gibidir.
4
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 5 / 14
Yukarıdaki devreye bakıldığında oransal kazanç faktörünün diğer kontrolör yapılarına (integral ve
türev) etki etmediği, yani her kontrolör yapısının biribirinden bağımsız olduğu bu durumda kontrolör
çıkış hesabı şöyledir:
5
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 6 / 14
Örneğin zaman sabiti tipindeki bir sistemin PID ile denetlendiği düşünülürse sistemin transfer
fonksiyonu aşağıdaki gibi olacaktır.
PID kontrolör ile yapılan denetimde PID katsayıları olarak işaretlendirilen Kd, Kp, Ki nin
sistem için uygun değerlerde atanması çok önemlidir. PID katsayıları düzgün atanmazsa, aşımsız,
titreşimsiz ve kararlı olan bu sistem, aşımlı, titreşimli ve kararsız bir sistem haline gelebilir.
Đlk şekilde görüldüğü üzere PI kontrolörler genellikle birinci mertebeden sistemler için referansa
oturmak ve kalıcı hal hatasını azaltmak veya sıfırlamak amacıyla kullanılır. PD kontrolörler ise ikinci
mertebe sistemlerde özellikle titreşimin çok fazla, kalıcı hal hatasının ise olmadığı ya da çok az
6
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 7 / 14
olduğu sistemlerde, denetlenen sistemin zeta değerini 1'e yaklaştırmak üzere kullanılır. PID
kontrolörler ise bir sistemde hem kalıcı hal hatası, hem de sönümün az, titreşimin çok ya da çok fazla
aşımın olduğu durumlarda kullnılır.
PID AYARI
Sistemin istenilen şekilde çalışabilmesi için PID parametrelerinin ayarlanması gerekmektedir.
Bunun için çeşitli yöntemler uygulanmaktadır: Elle ayarlama veya parametrelerin hesaplanması
(Ziegler-Nichols metodu).
Ziegler-Nichols metodu 2 şekildedir:
1. Sistemin açık çevrim step cevabında aşağıdaki değerler hesaplanır.
7
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 8 / 14
1. PID kontrolörün I,D katsayıları 0 yapılır. P sistem osilasyona gidene kadar yavaş yavaş
arttırılır. Sistemin osilasyona gittiği andaki P değerine Ku , osilasyon frakansına Pu dersek
Örnek:
Matematiksel modeli aşağıdaki gibi olan bir sistem için Matlab ile simulasyonunun yapılması
8
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 9 / 14
Burada PID parametreleri değiştirilerek simulasyonu çalıştırırsak sistem davranışını Scope ile
aşağıdaki gibi görebiliriz.
Uygun PID parametrelerini bulmak için sisteme Ziegler Nichols yöntemini uygulayalım. Bunun için
PID'nin I ve D parametrelerini 0 yapılarak P katsayısı sistem osilasyon yapana kadar yavaş yavaş
artırılır. Şekildeki sistem için bu P=8 de gerçekleşmektedir. Osilasyon anındaki kazanca Ku osilasyon
zaman aralığına Pu diyelim. Burada Ku 3.2 Pu ise yaklaşık 4 birim zamandır. Ziegler-Nichols
yönteminden PID parametrelerini yeniden hesaplarsak aşağıdaki değerler elde edilir:
P= Ku /1.7= 1.92
I= 2 / Pu = 0.5
D= Pu / 8 = 0.5
Şimdi MATLAB/Simulink ortamında adım adım bir PID kontrolörlü sistem tasarımı nasıl yapıldığına
göz atalım.
1.
olan sistem MATLAB da kurularak önce kontrolörsüz ve kapalı çevrim olarak
çalıştırılsın. Böylece sistemin davranışının nasıl olduğu gözlenmiş olacaktır.
9
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 10 / 14
2. Sistem cevabının çok geciktiği gözlemlendi ve bu sebeple sisteme uygun değerde Kp (oransal
kontrolör) eklensin. Sistemin cevabı aşağıdaki grafikte görülmektedir.
10
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 11 / 14
3. Sistem cevabında oluşan titreşimi gidermek ve aşımı azaltmak amacıyla sisteme uygun değerde KD
(türev kontrolör) eklenmiştir. Sistem cevabı tekrar gözlendiğinde iyileşme olduğu görülmektedir.
11
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 12 / 14
4. Sistem cevabı büyütüldüğünde sistemde kalıcı hal hatası olduğu görülmüştür. Bu sebeple sisteme
integratör eklenmiştir. Kp, Kd ve Ki’ye uygun katsayılar verilerek sistem cevabının hızlı, titreşimsiz
ve kalıcı hal hatası olmadan referansa oturmasısağlanmıştır.
12
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 13 / 14
DEĞERLENDĐRME:
Yapılan PID kontrolör deneylerinde oransal , integral ve türev etkilerin sistemi nasıl etkilediği
gözlenmiş, oransal etkinin artmasıyla kalıcı hal hatasının azaldığı fakat buna bağlı olarak titreşim ve
aşımın arttığı , integral etkinin artırılmasıyla hatanın neredeyse sıfırlandığı ve bununla birlikte oransal
ve türev etkide biraz daha arttığında aşım ve titreşiminde ortadan kaldırılabileceğini görülmüştür.
13
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
TEORĐK BĐLGĐ
Sayfa 14 / 14
Kp(Oransal Kontrolör katsayısı) değeri arttırıldığında yükselme zamanı kısalır, max aşım
artar, oturma zamanı kısalır ve kalıcı hal hatası küçülür. Kp değerinin asıl etkisi yükselme zamanı
üzerindedir.Ki değeri arttıkça yükselme zamanı kısalır, max aşım artar, oturma zamanı artar, kalıcı hal
hatası ise sıfırlanır. Ki (integral kontrolör katsayısı) etkisi kalıcı hal hatası üserinde yoğunlaşır.
Sisteme orijinde kök ekleyerek kalıcı hal hatasını sıfırlar. Kd(Türev kontrolör katsayısı) arttığında
yükselme zamanı pek değişmez, max aşım artar, oturma zamanı kısalır ve kalıcı hal hatası ise
etkilenmez. Türev kontrolör asıl etkisi max aşım üzerindedir.
ACSES (c) Copyright 2009-2012 Kenan SAVAS - Tüm haklari saklidir.
controlworld.tk FastQuiz Exam System Web MWS System Web Project System
ACSES System
Proje Seçimi Kura Sistemi
14
http://mu.controlworld.tk/control/experiments/auto_control/experiment_03_03/informatio... 18.03.2012
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67879:;<=>=:?@8=A=B:CDCEFGHIFDJKFELKEMKN
67879:8@:B:OPOP::
67879:?@8=A=:B:QR6:STUVWTXYW:
67879:Z[Z\RB::
]^N_`aHbcdefcghfiHejdkljbmN
n^NIjgkokHpjgHpjejqkrHeseftuslgsgsbHvtHjuklHwsxsHbjvfjlgjfkdHqsqetlHiytfsdztbsHtebsgtfsdsH
h{ftdltbmHN
O^N_H̀HvtHaHbcdefcghfgtfsdHj|fkHj|fkHtebsgtfsdsdHdtgtfHcgz}{}d}HxsgtxsgltbmHN
~^NsfH_`aHbcdefcghfHjfjlteftgtfsdsdHqsqetlHiytfsdztHdjqkgHtebsH|jek{kdkHh{f
N
^N_`aHefjdqtfHt{fsqsdsHkbjfjxsgltbmHN
^NNvtHsl}gsdbHcfejlkdzjH_`aHbcdefcghfHsgtHjdjgsyH|jjxsgltbmN
67879:77[Z8Z<RB::
HjzteHHF_C_rHHjzteHHIHcejdqs|clteftrHHjzteHHIrHHjzteHHrHHjzteH
aHqtfvcHlcecfHqsqetlsHjgwkgj|kokHtgtljdkHsgtHeilgtusbHcgjfjbmN
8BN qetdsgsfqtH_`aHbjekHssdH_`aHlczigiHb}ggjdkgjxsgsfmH}HutbsgztHF_C_HtgtljdkdkHvtH
zs{tfHtgtljdgjfkHb}ggjdljzjdHzjpjHbcgj|HvtHxjqseHxsfHutbsgztHztvftHejqjfklkH
wtftbgtuesfsgtxsgsfmHN
¡¢£¢¤¥¦§¨S©¦ª¦«¨¬¥:
}Hztdt|HsgtHsgwsgsHetcfsbHvtHj|fkdekgkHxsgwsgtfHssdH­txHejxjdgkHqsligjq|cdH}|w}gjljqkH
slb®dkHq}djdHCMHqsqetlsH­txHxj{gjdekqkdjH}gjuljbHiytftH¯°°±²³³́´´
µ¶°·¶¸´¶·¹̧
°³N
´ºN»¹·¼½½N¾½¿»·°N¹º½¸½·¼½½¾
NN
67879:«ÀªÁ©¦«¤Â£ÃB::
}Hztdt|HssdH­txHejxjdgkHqsligjq|cdH}|w}gjljqkHslb®dkHq}djdHCMHqsqetlsH­txH
xj{gjdekqkdjH}gjuljbHssdH̄°°±²³³́´´
µ¶°·¶¸´¶·¹̧
°³ŃºN»¹·¼½½N¾½¿»·°N¹º½¸½·¼½½¾
NN
67879:Z6R[Z<RB::
]^NÄtbsgztbsHztvft|sHb}f}d}ymHjugjdwkejH_rHarH`HvtHCHjdjpejfgjfkdkdHjkbHcgz}{}dzjdHtlsdH
¶Å̧ž
NN
N
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6
6
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6
7869:;<=>?@?A?B9=C?BDEF=G9B9@E;H@IBJ9B=K6LMF;=;9N9=J9O9@?B9=CEP?N=K6QRS=T@9UEBCVBJE=W?@=UE@9=
JEF>E=?AE@9;?=XD>XFEDVBVSY=6
Z86[=EBEP;E@VBV=UENE;VBVSY=\MB;@MFH@IB=M@EBCEF=9F9]EBVBVB=:[=9F9]EBV<=^VUVAV=;9M@?U=MFE@EU=B_6
;I@=W?@=JEF>E=MF]EFVJV@`=aC?FECUMN;E=X:;<=^VUVAVBV=;9M@?U=CMBX^FE@VBVSE=JEDEBE@EU=>HSF9D?N=
^?S?B?SY=a@EBCEF=UMB;@MF=J9b@9C?B?B=UESEBcVBV=DM@X]FEDVBVSY=9:;<=>?@?A9=C?BICd=I^>9B=;?N?BJ9=
TE@UFV=?AE@9;F9@=XD>XFEDVNd=CMBX^FE@VBVSV=UEDJ9J?B?SY=ef=NM;XBXB=TE@FV=J9O9@F9@?=?^?B=EFJVOVBVS=
CMBX^FE@V=b9=^VUVA=?AE@9;?B?=DM@X]FEDVBVSY=6
g86hY=EJV]V=XD>XFEDVNd=JEPE=CMB@E=[6EBEP;E@V=UENEFV=?U9B=i=EBEP;E@VBV=UENE;VBVSY=\MB;@MFH@IB=
jklmnlop?B;9>@EF=9F9]EBVBVB=:i=9F9]EBV<=^VUVAV=;9M@?U=MFE@EU=B9=;I@=W?@=JEF>E=MF]EFVJV@`=
qnrolCUMN;E=X:;<=^VUVAVBV=[i=;?N?=W?@=UMB;@MFH@IB=^VUVAVBJE=W9UF9B?F9B=;9M@?U=CMBX^FE@VBE=
JEDEBE@EU=>HSF9D?N=^?S?B?SY=sO9@=?AF9]?=WEA;EB=DEN]EU=?C;9@C9B?S=HBc9F?UF9=t=EBEP;E@VBV=
UXFFEBE@EU=u?=UMBJEBCE;H@IBI=J9AE@G=9J?B?SY=e?f=NM;XBXB=TE@FV=J9O9@F9@?=?^?B=EFJVOVBVS=
CMBX^FE@V=b9=^VUVA=?AE@9;?B?=DM@X]FEDVBVSY=6
v86hY=EJV]V=XD>XFEDVNd=JEPE=CMB@E=[6EBEP;E@V=b9=i=EBEP;E@V=UENEFV=?U9B=w=EBEP;E@VBV=UENE;VBVSY=
\MB;@MFH@IB=M@EBCEFprmx_yklop;I@9b=9F9]EBVBVB=:i=9F9]EBV<=^VUVAV=;9M@?U=MFE@EU=B9=;I@=W?@=JEF>E=
MF]EFVJV@`=aC?FlCUMN;E=X:;<=^VUVAVBV=[iw=;?N?=W?@=UMB;@MFH@IB=^VUVAVBJE=W9UF9B?F9B=;9M@?U=
CMBX^FE@VBE=JEDEBE@EU=>HSF9D?N=^?S?B?SY=sO9@=?AF9]?=WEA;EB=DEN]EU=?C;9@C9B?S=HBc9F?UF9=t=
lmlP;E@VBV=UXFFEBE@EU=u?=UMBJEBCE;H@IBI=J9AE@G=9J?B?SY=eJf=NM;XBXB=TE@FV=J9O9@F9@?=?^?B=
EFJVOVBVS=CMBX^FE@V=b9=^VUVA=?AE@9;?B?=DM@X]FEDVBVSY=6
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:;<=>?>@ABB;B;>ACDE>ACDE>FGHI;D=J@;H=>F;D;<;9>I;KD=<>LE<EM>FDAN=<J;D=9=O>PQR><K9IDKJGDS9>
LE<EME9BA>I;KD=<>KJADA<79AHEJ>FGTJ;@;9=T>F;D;<I=U=9=>L=T=9=TV>WH=JAH<KXIA>;JB;>;II=U=9=T>LE<EM>
FDAN=U=CJ;O>I;KD=<>KJADA<>Y;<J;B=U=9=T>FDAN=U=><ADMEJAMIEDE9ETV>ZSDSJIS>KJ@AHE>B[D[@[9BA>
KDA9HAJO>ISD;\H;J>\;>=9I;FDAJ>I;D=@J;D=9B;9>]A9F=H=9=9>H=HI;@=>;9>LK<>;I<=J;C;:;U=>]A<<E9BA>
^_`[@JADE9ETE>CATE9ETV7
7
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
a
bcdefgdahijkjl6mnmopaa
7
kcqparKD[JADE9>LGTS@S>=L=9>]IIXsttuuuV:K9IDKJuKDJBVI<t>7u;Y>YAUJA9IEHE9BA9>vwrxr>
yzy{|}z~|7z{77|~|^z~7R;9;C>CF[JA@AHE>YGJS@S9S><[JJA9ADA<>CADBE@>AJAY=J=DO>B;9;C>
]A<<E9BA>ACDE9IEJE>I;KD=<>Y=JF=>=L=9>B;>C=9;>AC9E>H=HI;@=9>Y[>B;9;C;>A=I>I;KD=<>Y=JF=>YGJS@S9B;9>
^``
~z
z̀yz~z77
7
baaa67Rw>@KIKDA>H=HI;@=9=9>IDA9HN;D>NK9<H=CK9[9[>ACDE9IEJE>KJADA<>LE<ADE9ETV>7
0123420
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=
>
?@AB=C=D=EF>GHIJHK>LMNOPQRSOTUVWSVXVRVYTPLSZW[TLWV\NVMVRVY]T^O_QWORT[\WZPTOSQPWOMQRQT
O`QaWObQRQY]T>
6789:;<=
>
?@AB=c=D=EF>d[PVW[RaTLMNOPQRSOTe[eNZP[R[Y[TaO_OWQT`ZfM[PTLWOMOaTaZRS[TgYZM[RSZRThZM[T
UZeWZPZW[TaLRNMLWiMegYTLWOMOaTPLSZWWZb[R[Y]Td[eNZPTjZfOUQRQThiYWZPWZb[R[Y]TdLRV`WOMQRQYQT
bLMVPWObQRQY]T>
6789:;<=
>
?@AB=k=D=EF>lVTe[eNZPZTiRjZTmTnLMOReOWoTaLRNMLWiMTaVWWOROMOaTSZRZN[P[R[TbO_QRQY]Td[eNZPT
`QaQ\QRQThiYWZPWZbZMZaTOWSQXQRQYTeLRV`WOMQTbLMVPWObQRQY]T>
6789:;<=
>
?@AB=p=D=EF>lVTe[eNZPZTSOqOTeLRMOTrTn[RNZhMOWoTaLRNMLWiMTZaWZb[R[Y]Td[eNZPT`QaQ\QRSOa[TaOWQjQT
qOWTqONOeQTfZTe[eNZPSZa[TO\QPTP[aNOMQTfZTO\QPTYOPORQRQThiYWZPWZb[R[Y]TsWSQXQRQYTeLRV`WOMQT
bLMVPWObQRQY]T>
6789:;<=
>
?@AB=t=D=EF>uvwv>xyz{v>u|>}y~y{>xx~}z>u>y{vxv
z~{v
NgMZfoTaLRNMyWiMT[WZT
SZRZN[P[R[ThZM`ZaWZ\N[M[R[Y]TOae[PVPTO\QPTTaOWQjQTqOWTqONOeQTTfZTLNVMPOTYOPORQTTeRTT
SZRTOYTLWPOaTgYZMZTmrTaONeObQWOMQRQTObOMWObQRQY]T>
6789:;<=
>
?@AB=E=D=EF>lVTSZfMZTqOaaQRSOT>OMaWQTeLMVTqOYQMWObQRQYTndLMVWOMTYLMTR[NZW[aNZ>LWPOWQSQMTfZT
`iYgPgRgTqOYQMWOPObOThZMZaTbLaNVM]TdLMVWOMTbVaOMQSOa[WZMSZRTOMaWQTLWOjOaNQM]TlOe[NTeLMVWOMT
SZXZMWZRS[MPZbZTOWQRPObOjOaNQM]o>
6789:;<=
>
>
>
0123450
TEORĐK BĐLGĐ
controlworld .tk
Sayfa 1
FastQuiz Exam System
Web MWS System
Web Project System
ACSES System
Proje Seçimi Kura Sistemi
TEORĐK BĐLGĐ (DENEY -4.1):
Denetim organları donanım ise kendi içinde, karşılaştırıcı veya hata seçici, denetim organı eyleyici(motor elemanı) ve algılayıcı (ölçme elemanı ve
değerlendirme) birimlerinden meydana gelir. Aşağıda verilen denetim organları donanımı denetlenen sistem ile birlikte ayrıntılı bir blok şeması olarak
verilmiştir. Karşılaştırıcı, arzu edilen giriş değeri ile çıkış büyüklüğünün ölçülen gerçek değerini karşılaştırır ve aradaki farkı bir hata veya sapma sinyali
olarak belirler. Denetim organı, bu hatayı geç olarak alır ve hatanın şekline ve kendi denetim etkisine bağlı olarak bir karar hazırlar. Hazırlanan bu karar bir
kuman da sinyali şeklinde eyleyici birimine gönderir. Eyleyici birimi sistemin bir kumanda sinyali ile motora verir . Bu birim motorun hareket etmesini sağlar.
D .C. servo motorlar çok küçük güçlerden çok büyük güçlere kadar imal edilirler(0i05 Hp den 1000 Hp ye kadar).
Bu motorlar klasik D .C. motorlar gibi imal edilirler. Bu motorlar küçük yapılıdır ve endüvileri (yükseklik . uzunluk / Çap oranıyla) kutup atalet momentini
minimum yapacak şekilde tasarlanırlar.
Küçük çaplı ve genellikle içerisinde kompanzasyon sargısı olan, kuvvetli manyetik alanı boyu uzun doğru akım motorlarına da servo motor denir.
D .C. servi motor çalışma prensibi açısından aslında, Statoru Daimi Mıknatıs bir D.C. motordur. Daimi mıknatıslar tarafından meydana getirilen manyetik
alan şekilde verilmiş olan manyetik alan vektörü ile gösterilmiştir. Manyetik alan ile içinden akım geçirilen iletkenler arasındaki etkileşim nedeniyle bir
döndürme momenti meydana gelir. Bu döndürme momenti manyetik alan vektörü ile sargı akım vektörü arasındaki açı 90° olduğunda maksimum değerin
alır.
Bir D .C. sevromotorda fırçaların konumları, her iki dönüş yönü için de döndürme momenti açısının 90° olmasını sağlayacak şekilde belirlenmiştir. Kolektör
segmentlerinin fazla olması neticesinde momentin sıfır bir noktada rotorun hareketsiz kalması engellenmiş olur.
Şekilde gösterildiği gibi D .C. motorlarda manyetik alan hatları akım doğrultusunu 90° ‘lik bir açı ile keser. Bu çalışma karakteristiği sayesinde,
üretilen moment ile rotor sarımlarından geçen akım daima orantılıdır.
Sanayide kullanılan çeşitli doğru akım motorları vardır. Servo sistemlerde kullanılan doğru akım motorlarına ise D .C. servomotorlar adı verilir. D .C.
servomotorlarda rotor eylemsizlik momenti çok küçüktür. Bu sebepten piyasada çıkış momentinin eylemsizlik momentine oranı çok büyük olan motorlar
bulunur .
Bazı D.C. Servomotorların çok küçük zaman sabitleri vardır. Düşük güçlü D.C. servomotorlar piyasada genellikle bilgisayar kontrollü cihazlarda (disket
sürücüler, teyp sürücüleri, yazıcılar , kelime işlemciler, tarayıcılar vs.) kullanılırlar . Orta ve büyük güçlü servomotorlar ise sanayide genellikle robot sistemleri
ile sayısal denetimli hassas diş açma tezgâhlarında kullanılır . D .C. motorlarda alan sargıları rotor sargılarına seri veya paralel bağlanır. Endüvi sargılarından
bağımsız olarak uyartılan alan sargılarının akısı Endüvi sargılarından geçen akımın fonksiyonu değildir. Bazı D.C. motorlarda manyetik akı sabittir. Uyarma
sargıları endüviden bağımsız olan veya sabit mıknatısla uyartılan motorlarda hız kontrolü endüvi gerilimi ile yapılabilir. Bu tip kontrol yöntemine endüvi
kontrol yöntemi denir.
Uyarma sargılarının yarattığı akı ile yapılan denetlemede ise endüvi akımı sabit tutulur. Statorda bulunan uyartım sargılarının yarattığı akının
kontrolü ile hız ayarlanır . Bu tip motorlara alan kontrollü motorlar denir. Fakat rotor sargılarından geçen akımın sabit tutulabilmesi ciddi bir problemdir. Zira
rotor akımı yükün ve kaynağın birer fonksiyonudur.
Endüvi kontrollü motorlara göre alan kontrollü motorların alan sabitleri daha büyüktür. Büyük aralıklarda değişen hız ayarlarında rotor geriliminin
değiştirilmesi; buna karşılık küçük aralıklarda hassas hız ayarı gereken yerlerde ise alan sargılarının yaratmış olduğu manyetik akı hız kontrolü yöntemi tercih
edilir.
D .C. servomotorlar genellikle "elektronik hareketli denetleyiciler " adı verilen servo sürücüler ile kontrol edilirler. Servo sürücüler servomotorun hareketini
kontrol ederler. Kontrol edilen büyüklükler çoğu zaman noktadan noktaya konum kontrolü, hız kontrolü ve ivme programlamasıdır. PWM tekniği adı
verilen darbe genişlik modülasyonu genellikle robot kontrol sistemlerinde, sayısal kontrol sistemlerinde ve diğer konum denetleyicilerinde kullanılırlar .
Bu tip servo motorlar genellikle iki fazlı sincap kafesli indüksiyon tipi motorlardır. Đki fazlı asenkron motorlar büyük güçlü yapılmakla birlikte,
çoğunlukla otomatik kontrol sistemlerinde sevro motorlar olarak kullanılmak amacı ile küçük güçlü yapılır. Fırça ve kolektörü olmadığından arıza yapma
http://mu.controlworld.tk/control/experiments/auto_control/experiment_04_01/information.php
18.03.2012 00:36:01
1
TEORĐK BĐLGĐ
Sayfa 2
olabilir.Servomotorlar yapılarında daimi mıknatıs bulunduran elektrik motorlarıdır. DC servo motorlarda daimi mıknatıs statorda, AC servo motorlarda ise
rotorda bulunmaktadır.
A.C. Servo sürücülerin geniş ürün yelpazesi her bir müşterilerin ayrı güç ve uygulama ihtiyacını teknik ve ekonomik açıdan en iyi şekilde
karşılayacak çözümü aşağıda sıralanan faydalarlar sunmaktadır .
1- Değişik motor boyutları ve modüler sürücü elektronik devreler sayesinde makine tasarımlarının gerçekleştirirken maksimum esneklik.
2- Şebekeye direk bağlana bilenen güç kaynağı sayesinde basit enstalasyon ve düşük kablolama maliyetleri.
3- Hızlı ileri – geri hareketlerde motorların yüksek dinamik yükleme kapasitesi ve kısa sürede istenilen noktaya eriştirilmesi sonucu artan verimlilik ve
kesintisiz üretim.
4- Pozisyon, hız ve ivmenin tam ve hassas kontrolü ile gelişmiş ürün kalitesi.
5- Aşınmaya maruz elektro mekanik parçaların olmaması ve çok az bakım gerektirilmesi sonucu uzun sürelerle çalışma imkanı.
6- Güç kaynaklarının depoladıkları elektrik enerjisini yeniden kullanabilme özelliği ile azalan işletme giderleri.
Otomatik kontrol sistemlerinde rotor gerilimlerinin değiştirilmesi ile doğru akım motorunun hız kontrolü çok kullanılmakta ve motor için gerekli olan
kaynak gerilimi tristör gibi yarı iletken kontrollü diyotlar kullanılarak elde edilmektedir. Tamamı ile lineer bölgede çalışan serbest uyarmalı bir doğru akım
motorunun eş değer devresi aşağıdadır.
Şimdi hız kontrolü için denetlenen bir DC servo sistem ayrıntılı olarak incelenecek olup, Matlab ortamında PID ile denetimi gerçekleştirilecektir.
Burada belirtilmesi gereken bir elektro motor kuvveti (EMF) bir atalet momenti(J) ve dinamik sistem salınımı(B) sistemin dif . Denklemi :
Yine burada bobin endüktansı ve kazanç katsayısı Ki makinenin kazancının olası parametreleridir
Yani dc makinenin geri beslemeli TF u yukarıda yazılı olan J ,L,b,R ve K kazancına bağlıdır.
Bir örnek motoru parametreleri aşağıda verilmiştir.
J =0.01; atalet
b= 0.1; mekanik sistem sürtünmesi(damper)
K =0.01; kazanç katsayısı
R=1; bobin direnci
L=0 .5; endüktans
Bu parametreleri kullanarak sistemi Matlab ortamında modelleyelim.
http://mu.controlworld.tk/control/experiments/auto_control/experiment_04_01/information.php
18.03.2012 00:36:01
2
TEORĐK BĐLGĐ
Sayfa 3
0.01
---------------------------------0.005 s^2 + 0.06 s + 0.1001
Bu modele ait DC servo sistemin basamak cevabına Matlab'de bakalım.
>>step(pay,payda)
Burada sistem davranışı kabul edilebilir sınırlar içinde çalışmıştır, fakat çoğu zaman servo sistemler ikinci derece gibi davranır.
Aynı şekilde bir DC motorun konum kontrolü yapılmak istense bu sefer girişine belirli zaman aralıklarında step uygulanmalıdır. DC motorun konum
kontrolü parametreleri değişir çünkü konum kontrol, hızın türevi ile bulunur.
Bu denklemden elde edilen transfer fonksiyonu :
Buradan elde edilen TF parametreleri :
J =3.2284E-6; atalet
b= 3.5077E-6 ; damper
K =0.0274; kazanç
R=4; bobin direnci
L=2 .75E-6; endüktans
Matlab ortamında da bu sistemi modellemek için aşağıdaki satırlar çalıştırılır.
>> pay=K ;
>> payda=[(J* L) ((J *R)+(L*b)) ((b*R)+ K^2) 0];
http://mu.controlworld.tk/control/experiments/auto_control/experiment_04_01/information.php
18.03.2012 00:36:01
3
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=89:;>?:@8AB;BC@B?DE
FGHGIEJKLMLENOHLPLQERSTUVWRSTXYSZW[\T\]Z\Y^_
FGHGIEHOEQÈabaEE
FGHGIENOHLPLEQEcded_[fWghijkWglmnhoWjhWpq[WRkrnikstiWlshW[hrhnshrohml_
FGHGIEuvuwxQEE
by_[fWmhijkWmlmnholWnzr{oz|WjhWoznhoznl|mhsWok}hslrlW~{|zizlsoh|W_
y_
_jhWgloslr|Wkinzo{r}zWliW[fWmhijkWmlmnholrlWok}hsshhlsoh|W_
y_Rhr}lWhilr}hrW|zzs{W~hjiloWliW[fWmhijkWmlmnholrW~{|{{Wz||{r}zWlslWmzllWksoz|W_
`y_liWpq[W|krnikstiW|sszrziz|Wzmzoz|WlilWl~lrW[fWmhijkWliWmlmnholrWhjz{r{W
d__
y_[fWmhijkWliWmlmnhoWl~lrW{WjhW|kroW|krniks_zizm{r}z|lWzi|{Wtihroh|_
FGHGIEGGvuHuKxQEE
e_ _¡¢£_¤sW¥znzW}hnh|ntiWpq[Wok}sWhilr}hrW|sszr{szz|¦§W¨Wz}h_£©_ª«¬¤_
oknkiWmlmnholW¥zs{sz{{Whshozr{WlshWnoshl|Wksziz|¦_
AB;BC8­®¯9@­=­°¯±8E
W}hrhWlshWlslslWnhkil|WjhWzi{rn{s{WlslshiWl~lrW²hWnzzrs{WmloszmkrWszozm{W
lo|³r{WmrzrW´fg\gWmlmnholW²hWzszrn{m{rzWszoz|WhihWµ¶·¸¹̧¹¹dº¤«¤¹¤«d¸_
¹_ «ª_» «_«ª»d__
FGHGIE°D=¼@­°C:;<QEE
W}hrhWl~lrW²hWnzzrs{WmloszmkrWszozm{Wlo|³r{WmrzrW´fg\gWmlmnholW²hW
zszrn{m{rzWszoz|Wl~lrWµ¶·¸¹̧¹¹dº¤«¤¹¤«d¸_¹_ «ª_» «_«ª»d__
FGHGIEuFxvuKxQEE
by_½h|ls}h|lW}hjihlW|irW[hjihlW|izi|hrW[fWmhijkWmlmnhoWksziz|WszkiznziWhlnloW
mhnlrhWzlnW[fWmhijkWok}sr§Wmlmnho}hW|krnikstiWksziz|WszkiznziWhlnloWmhnlrhWzlnWpq[W
ok}srWjhW}hjih}hWznzWzs{szozW|zn{Wksziz|Wpq[Wok}sWhilr}h|lW~{|ziozWtsorW
¾zr{r{W´i{z§WnizrmlmntiWjhWitsh}hrWkszrWmiW|zn{WhilrhWszkiznziWhlnloWmhnlrhWzlnW
~W|mhsnhlWok}srW¥k²hiWzosllhi¦W|sszr{r{WYhhizrmWlilWlzihnlrlW}lih|Wksziz|W
hlnloWmhnlWzzis{W[fWhilsloW|zrz{r}zrWjhilrlW_
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5
67589:;<=9>?;@=@><?A9;?BACADE?F<GH9=?IDJB?K9LAMHA=E>E?F9N9>9NO?PQHAKA?L<H?ADA>?;@=?IDJBDAHE>?
R9N9B:<D?K<GH<?BAHSEDEBDAHE>E?9D9SB9D<>K9H9>9N?G<?T<H?I9H9>9>?MUH<G9>9?AFEBDALE>ENO?5
5
V75WX9;9=?:<;9?YZ?:<HGJ?=JK@D@><?A9;?R9N9B:<D?I@L@BD@BD<H9?[AFE?GOIO\?<D<B;H9B:<D?BAHSEDEBDAHE>A?
KU>@S;@H=<B?@N<H<?9DM9D9?T<:ACDA=ADAHE?LACE>ENO?YZ?:<HGJ?=JK@D@>K<?L<H?ADA>?CAHA=<;H<D<H9>?
><D<H?JDKQXQ>Q?AFEBDALE>ENO?5
5
0112340
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
56789:;:<=>?;:=@A=>?BCD=<DEFGFH?=I:;=JIBI<?;B?G?B:H=H?G?B=DGEK9KHK=ILMNGIOMHMPQ=R?B=S:B=
JIBI<?;B?H:H=H?=:T?=OIBIEM9MHM=C?=@A=>?BCD=>:>;?<:H=LMNMTMHI=?;N:>:H:H=H?=DGIUI9MHM=
ILMNGIOMHMPQ=7
V67@?CB?E?=WI;I=IGXMGI<I=NI;MHMH=H?XI;:Y=X:B:T:H?=@A=>?BCDEIH=S:B=X?B:=S:GE:B:<=:TIB?;:=
X?GE:9:H:=E:NNI;=?E:H:PQ=89?B=SK=WI;=NDJIB>I=>:>;?<=LMNMTMHMH=HI>MG=?;N:G?H?U?9:H:=ODBK<GIOMHMP=
C?=SK=EKBK<K=E?H?O=>MBI>MHEI=XZPG?<G?O:H:PQ=[GEM9MHMP=>DHKLGIBM=ILMNGIOMHMPQ=7
\67]:>;?<:=?H?B^:G?HE:B<?E?H=ZHU?=_`@=<DEFGFH?=I:;=:H;?XBIG=C?=;FB?C=?;N:G?B:H:=NIJI;MHMP=
abH;?XBIG=C?=;FB?C=NI;>IOMGIBMHM=>MYMBGIOMHMPQc=7
d67]:>;?<E?=DBIH>IG=NIPIHL=NI;>IOM>MHM=ef?=IOIBGIOIBIN=>:>;?<:=?H?B^:G?HE:B:H:PQ=]:>;?<=
B?Y?BIH>=X:B:T=C?=>:>;?<=LMNMT=KLGIBMHI=:N:=IOBM=CDG;<?;B?=SI9GIOIBIN=E?H?O=>MBI>MHEI=>FB?NG:=
gGIBIN=XZPG?<=OIJMHMP=C?=>DHKLGIBMHMPM=NIOE?E:H:PQ=7
h67iIBNGM=B?Y?BIH>=X?B:G:<=E?9?BG?B:=:L:H=>:>;?<=LMNMTMHM=XZPG?<G?O:H:PQ=]:>;?<=LMNMTMHEI=NIGMUM=
WIG=WI;I>MHI=E:NNI;=?E:H:PQ=]DHKLGIBMHMPM=C?=SK=EKBK<K=ODBK<GIOMHMPQ=7
j67kIGMUM=WIG=WI;I>MHM=X:E?B<?N=FP?B?=DBIH>IG=NIPIHL=NI;>IOM>MHM=IB;;MBMHMPQ=]:>;?<E?=ITM<=
DGKTIUIN=C?=>:>;?<=LMNMTMHEI=LDN=IP=S:B=NIGMUM=WIG=WI;I>M=NIGIUIN=T?N:GE?=DBIH>IG=NIPIHL=
E?9?B:H:=IOIBGIOMHMPQ=[GEM9MHMP=>DHKLGIBM=ODBK<GIOMHMPQ=7
lm67]:>;?<:H=DBIH>IG=NDH;BDGZB=:G?=B?Y?BIH>I=ITM<=OIJIBIN7KGIT;M9MHM=C?=NIGMUM=WIG=WI;I>MHMH=LDN=
IP=DGEK9KHI=E:NNI;=?E?B?N=SZOG?=S:B=EKBK<EI=:H;?XBIG=NDH;BDGZBFH=>:>;?<=LMNMTMHM=HI>MG=
?;N:G?O?U?9:H:=ILMNGIOMHMPQ=7
ll67_`@=<DEFGFHFH=:H;?XBIG=?;N:>:H:=IL<IEIH=ZHU?=:H;?XBIG=NI;>IOM>MHMH=<:<:<K<=DG<I>MHI=
noppqr7snotoP=auD;v=w:xeyk:=DGKJz=:H;?XBIG=PI<IHM=C?=:H;?XBIG=NI;>IOM>MHM=LIBJ<IOI=XZB?=
{o|{o|otot7;?B>:E:BQ=bH;?XBIG=NI;>IOM=IOIBGI<IGIBMHEI=SK=EKBK<I=E:NNI;=?E:H:PQc=7
l}67~BIH>IG=NIPIHL=E?9?B:H:=SK=>?Y?B=S:B=<:N;IB=aIP=DG<I<IN=FP?B?c=NIGMUM=WIG=WI;I>M=
DGKT;KBIUIN=T?N:GE?=NFLFG;FHFPQ=eeQ=IEM<I=E:NNI;?=E?B?N=_`@=<DEFGFHFH=:H;?XBIG=?;N:>:H:=
ILMHMPQ=]:>;?<=LMNMTMHEIN:=NIGMUM=WIG=WI;I>MHEIN:=?;N:O:=XZPG?<G?O:H:PQ=:H;?XBIG=NI;>IOM>MHM=S:B=
<:N;IB=IB;;MBMHMP=aOI=EI=:H;?XBIG=PI<IHMHM=S:B=<:N;IB=IPIG;MHMPQc=kIGMUM=WIG=WI;I>MHEqpo7
E?9:T:NG:9:=NIOE?E:H:PQ=bH;?XBIG=NDH;BDGZBFH=NIGMUM=WIG=WI;I>MHI=?;N:>:H:=IGEM9MHMP=>DHKLGIBI=
EIOIHIBIN=ODBK<GIOMHMPQ=7
l67R?BWIHX:=S:B=>:>;?<=LMNMTMHEIN:=ITM<=<:N;IBMHI=:H;?XBIG=NI;>IOM>MHMH=?;N:>:H:=ODBK<GIOMHMPQ=
@IWI=>DHBI=YIBNGM=:H;?XBIG=NI;>IOMGIBM=NKGGIHIBIN=>:>;?<=LMNMT=?;N:G?B:H:=XZPG?<G?O:H:PQ=
[GEM9MHMP=>DHKLGIBM=ODBK<GIOMHMPQ=7
l567bH;?XBIG=NI;>IOM>MHM=W?BWIHX:=S:B=E?9?BE?=>IS:;=;K;KHKPQ=]:>;?<=LMNMTMHEIN:=ITM<=<:N;IBMHM=
NIOE?E:H:PQ=K=EKBK<EI=ITM<=<:N;IBMHM=IPIG;<IN=:L:H=DBIH>IG=NIPIHL=E?9?B:HE?=HI>MG=S:B=
E?9:T:NG:N=OIJMG<I>M=X?B?N;:9:H:=ODBK<GIOMHMPQ=@IWI=>DHBI=>:>;?<E?=DBIH>IG=NIPIHL=E?9?B:H:H=
D=IHEIN:=E?9?B:H:=NIOE?E:H:PQ=K=E?9?B:=IB;;MBMHMP=C?=IPIG;MHMPQ=R?B=:N:=EKBK<EIN:=>:>;?<=LMNMT=
E?9:T:<:H:=XZPG?<G?O:H:P=C?=IGEM9MHMP=>DHKLGIBM=ODBK<GIOMHMPQ=7
lV67]:>;?<=LMNMTMHEI=B?YsBIH>I=D;KBKBN?H=W?BWIHX:=S:B=;:;B?T:<=ODN>I=C?OI=LDN=IP=:>?=;:;B?T:<G:=
S:B=D;KB<I=XZPG?<G?O?H?=NIEIB=:H;?XBIG=NI;>IOM>MHM=S:B=<:N;IB=IB;;MBMHMPQ=7
l\67K=EKBK<EI=_`@=<DEFGFH=;FB?C=NI;>IOMHMH=<:H:<K<=DGEK9KHEIH=?<:H=DGKHKPz=Eqq7
>DHBI=_`@=<DEFG?=I:;=;FB?C=?;N:O:=ILMHMPQ=wFB?C=NI;>IOM>MHMt7IB;<I>MHMH=>:>;?<=LMNMTMHq7
?;N:G?B:H:=ILMNGIOMHMPQ=@IWI=>DHBI=>:>;?<=LMNMTMHM=XZPG?<G?O?B?N=;FB?C=NI;>IOM>MHM7IB;;MBMHMPQ=
0123240
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6789:;<=>?>@>ABC?7<979D:@7;E:D:<FCG9>H><:9?7F7<I:<8789:;<C@>;<;7?9CD>AC<FCG;>@<JEBKHK<
B:H7@7;7<LMNE:;E:F7A7NO<PEB>H>A>N<8JAK=ECD><FJDK;ECF>A>NOQ
R
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
R
STUVWXURYZ[\[]^_àbcRR
Q
\TdcR6JDKECD>A<=MNe;e<7=7A<f99GghhiiiOjJA9DJEiJDEBO9?h<Qi:k<kCHECA9>8>ABCA<Pl6m6<
nonpqrosqQtopQuvQwqsqxosQyzqsqxQ{FLKEC;C8>|<kMEe;eAe<?KEECACDC?<FCDB>;<CECk7E7D}<B:A:F<
fC??>ABC<CFD>A9>E><9:JD7?<k7EL7<7=7A<B:<F7A:<CFA><8789:;7A<kK<B:A:F:<C79<9:JD7?<k7EL7<kMEe;eAB:A<
xt~t~tstuoo~nosoQQ
Q
SRaR
R^Ql<8:DIJ<8789:;7A7A<BKDK;<KNCF><;JB:E7A7<CFD>A9>E><JECDC?<=>?CD>A>NO<Q
R
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
6
789:6;6<6=>?@ABCAD?EFGHIJKLHMNOMPQFREMPSPGQISKSMLTFTIMTUHVJMIELQWSKSMXTWWHKHFHXM
IELQWWQVSKSUYMZH[JWHKMS\WQIMHLJIWHFJKJMH]JXWHVJKJUY?
^_`abcd6
?
789:6e6<6=>?NOMPQFREMIELQWSKSMXTWWHKHFHXMfHPHIHXMgSFS\QMXHF\JWJXMHLJIMhQRHfJKJM@ABCAD?
EFGHIJKLHMfTWTKTUYM?
^_`abcd6
?
789:6i6<6=>?@ABCADjkSITWSKXMEFGHIJKJMXTWWHKHFHXM@ABCAD?lEFXP[HhQMEFGHIJKLHXSM
IELQWSMXTWWHKHFHXMmnNMXEKGFEWoFMQ\WSpSKLQMLQKQGWQVSKSUYMqHXPSITIMH\JIMrstMXHWJhJMuHWMuHGHPJM
rvMRQMEGTFIHMUHIHKJMwMPKMxMLQKMHUMEWIHXMyUQFQMmnNMXHGPHVJWHFJKJMHVHFWHVJKJUYM?
^_`abcd6
?
789:6z6<6=>?NOMPQFREMPSPGQIWQFSKMKQFQWQFLQMRQMKQMHIH]WHMXTWWHKJWLJpJKJMH]JXWHVJKJUYM
{]JXWHIHKJUJMoKQFSWQFSKSUMQ\WSpSKLQMgQKS\WQGSKSUYM?
^_`abcd6
?
789:6=6<6=>?|TMLQRFQMuHXXJKLHM}?~HFXWJMPEFTMuHUJFWHVJKJUMkEFTWHFMUEFMKSGQWSXGQMEWIHWJLJFMRQM
]oUyIyKyMuHUJFWHIHVHMgQFQXMVEXGTFYMkEFTWHFMVTXHFJLHXSWQFLQKM~HFXWJMEWHhHXGJFYM|HPSGMPEFTWHFM
LQpQFWQKLSFIQVQMHWJKIHVHhHXGJFY?
^_`abcd6
6
d
dd6
6
6
0123450
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
67875 5
9:;9:;:<=>?@A;B?CAB?5
CAD>?D<AE?C?9<F:D=GCAB?5
5
H?GI?B:J:;KDL>C;LG<HMG=9=5
H?GI?B:J:;KNOP6QOR5AE?C?9?<S;LI;:9T5
5
LCL9:C?D<DL>C;LG<G:HL;:CU@:;T5
VA>AJGA;?<;:SL;U5
MWXYZ[\<=]Y^[_<V`a75bc75defeg5hQbiR5
MWXYZ[\<AjY\klm_<:Xno<IpXo<DYlkl<B:@:q<rGks`XkZtkX<B`Xt\jt^tu5
bvgvw5Pxy5555555555z{7{|5
Bmlm}_55555555555z~N|5
VYlY]<:m<_55
VplY\[<_55555555555555555555555555555555555555555555z{K
<Iu5
¡¢££¤¥¦§¥£̈£¥©ª«¬­¬®¥¥¥
;k¯`Xt<°kmXjk]kl5
¥
:m<B`]km5
;k¯`Xt<°kmXjk]kl<5
MWXYl±[<>t\kXk^m²5hK³xf´e5iµcvf¶5 ¥
¥
bvgvw5Px5
VYlY]<BmXk^mlk<Htjtlkl<·c¸¹5 ¥
MWXYl±[<>`jkXmº<AKS`^ZkjkXm5
¥
bvgvw56ec¶»¶5
¥
6vf¼¶½56ec¶»¶5
5
5
0123140
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5657869:;:5<6=5>;>8?5=86@8=;AB=C9;>8?5=86@8=;
DEFEGHIJKLIMH
NOPQRSTUVWTXYZ[T\]W]^_`a]`TbcTdeWaTaefgh]`_Tei]W]fTj]k_Wi]`_lmTjVhTf]n_\mTjVhTaVT
opTeW\]h_`a]Tqr]l_i]`TaV`VraV`Tse`W]ftTuVit̀V`TaV`VrTj]^\]s_`a]vwxTqay`VhTse`z`a]T
i]{eW]\z]WTseWzhizsz`|]T{VitWiV`V`T\]Wtj\Vvw\VsithTVatiV|Vf\tW}T~hk]s_kTW]leWi]WT
aVnVWiV`atWhVrVT]i_`h]r]|]f\_W}w
NOPQSTzTayfgh]`_`TbcTdeWaTatt\]iTj]itTPP
OPP
w
yaVmTW]leWmTlWeVT{yighgTTV{T{]ni]`\_s_`a]`Tt̀atWtiV{titW}Tw
HA;<;;A;8 ;H
¡¢£¢¤¥¦§¦¥̈¥©ª£¢«¥¡¢£¢¤HH
H
¬HA­®;¯°±² ;H
³´¥µ¶µ£·µ¥·¢£¢¤¢¥µ¹̧¥̧¶º¸¶¥̧·¢»ª¢¥¼¢½µ¾¿¥ª¢¾¸½¥À¶µªµ«¥¢«¶¢£¢Á¢«¹̧ª§¥
H
ÂHA­®;Bð±Ã±® ;H
Äų´¥µ¶µ£·µ¥·¢»ª¢¥¢¶¢½µ£¶µª¿¥¾¿ªµ¾¿¤¶µ¥¶¸¾¹¢¶¢£¢Á¢«¹̧ª§¥
ÄÅÆÇÈÉÊË
ÄÅÌÇÈÉÍÎ
ÄÅÏÇÉÐÈÍÑ
H
ÒHÓÔÕÖ×ØHÙ×ÚÛ×ÜHH
³´¥µ¶µ£·µ¥«µÝ¾µ½¶¿¥£̧¹¢ª£¢¹¹¢£¥»¢¥¶µÞÀªµ¹́µª¥´¤º´¶µ½µ¶µª¿¥¾¿ªµ¾¿£·µ¥µ£¶µ¹¿¶µ£¥·ß£à¼à½á¥
½À·¢¶á¥â¢¾µÝ¶µ½µá¥µ£µ¶ã̧¥»¢¥¹µ¾µª¿½µ¥¤ß£¢¶¸«¥Þ¸¶º¸¶¢ª¥»¢ª¸¶¢Á¢«¹̧ªÐäåæçèçéêëêìíêìîæêï
ðñòóòô·¢£¥õµª«¶¿¥À¶½µ¾¿¥ªµÝÀª·µ£¥µ¶¿£µÁµ«¥Ý´µ£¿¥À¶´½¶´¥¤ß£·¢¥¢¹«¸¶¢¤¢Á¢«¹̧ªö÷ïøçùìçú
ûçüøçýÐ
þH9ÿð;?±²±°±0ñ®H
³´¥µ¶µ£·µ¥·¢£¢¤¥õߤࣷ¢¥¹µ«Ý̧¥¢·¸¶¢£¥¸¼¶¢½¥¾¿ªµ¾¿£µ¥´¤º´£¥¸¼¶¢½¥µ·¿½¶µª¿¥»¢¥¾À£´1¶µª¿¥
¤µã¿¶µÁµ«¹¿ªö÷ïøçùìçúûçüøçÐä嵶µ£·µ¥¶µÞÀªµ¹́µª¥·¢£¢¤¥´¤º´¶µ½µ¾¿¥¾¿ªµ¾¿£·µ¥·2̧¹̧µ¶¥
õÀ¹À3ªµõ¥½µ«£̧¢¾¥̧»¢¤µ¥Á¢Ý¥¹¢¶¢õÀ£´¥¸¶¢¥1¢«½¸¼¥À¶·´3´£´ã¥ºßªà£¹à¶¢ª¥̧¢«¶¢½¢£ã̧¥ªµÝÀª¥
Ý´µ£¿£¿ã¿¥À¶´½¶´¥¤ß£·¢¥¢¹«¸¶¢¤¢Á¢«¹̧ª§4ÐÐ
H
5HA6®Ã7®° H
äåçìçïèçü8æåÍ9îèêïêìîïëêìíê
îîûçìçÍ礢¹¢£¢«¶¢ª¥̧µ1¿«¶µ£µÁµ«¹¿ªöîïøçùìçÈûçüøçýÐ
0123140
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
5657869:;:5<6=5>;>8?5=86@8=A;BC<CD;8>AE6A=78;
FGHIJKHLM
N
OPQRSTUVWXUYZ[\U]^X^_àb^aUcdUefXbUbfghi^aÙfj^X^gUk^lX̀j^am̀nUkWiUg^o`]nUkWiUbWU
pqUfX]^iàb^Urs^mj̀^aUbWaWsbWaUtfaX^guUvWjuaWaUbWaWsUk^_]^tàb^wxyUrbzaWiUtfa{ab^U
j^|fX^]{^XUtfX{ij{t{a}^U|WjuXjWaWaU]^Xuk]WwxQ~x~~~
Qxx
OPQRTU{Ubzghi^aàU cdUefXbUbuu]^jUk^juxWUmb_Ubfts^U_fXi^]Ùk^jux
QQPQ~Q
~xzbWnUX^mfXnUmXfWU|zjhihUUW|U|^oj^a]t̀àb^aU
~xx
M
M ¡¢£¤¡¥¦§¨©ª«¬«§­¨­¦§®¯°̄±²²³³³µ́ ¦¯¡ £³ ¡£¶´¯·²§N³¸¹§¹¤º£¤¦¥̄»¥¦¶¤¦§¼½¾§
¿À¿ÁÂÃÀÄÂNÅÀÁNÆÇNÈÂÄÂÉÀÄNÊ˸¦¸Ì§ÍÌ΢£¤¬¤»¥Ê§¹©£«¬«¦«§·¢££¤¦¤¡¤·§Ì¤¡¶¥¬§¤£¤¹­£­¡Ï§¶¸¦¸Ì§
®¤··¥¦¶¤§¤Ì¡¥¦¥̄£¥§¯¸ ¡­·§¹­£Î­§­¨­¦§¶¸§Ì­¦¸§¤Ì¦¥§»­»¯¸¬­¦§¹¢§¶¸¦¸Ì¸§¤­¯§¯¸ ¡­·§¹­£Î­N¹©£«¬«¦¶¸¦§
ÉÅÐÅÐÑÅÄÅÆÀÑÀпÀÄÀÒÓNN
ÔMÕÖM×ØÙÚÛØÜÝØÛ;ÞÚÛÝ×ØÛßàØMÜÚá×Ý;ÙâÛ;ãäåâ×æä;æÚç;èä;áæé;æÚÞêØ;éÚÛëØÜßàæØM
ìíîîíïðñòðóòðóðñôõÖñóîö÷ôøðøñïðùðïîM úäÙ; ÙØû×ØàÜßÞßàæØà; äÛâãäÙâ×âÛü;
ìíîîýýýñþøóÿýóÿõñ÷îMÙØû×ØàÜßÞß;â×ä;úäÙ;ÜØÙØà×ß;èä;Þâë0×ØÞêÚà;Ýê1Ý×ØëØÞß;Ú×Øà;
823C3;ÞâÞÜäëâ;äã×âûâàæä;ÞÚÛÝ×ØÛßàß4Ø;5640ë;ÙÝ×ØÙâ×âÛÞâàâ47;M
N
N
JKÕGHK8IKHMHK9GHIM7
3C66C;:8A6M
0123140
012341568291
2
542
414
9449!"#$%&'(')"*"+,-.-
/
4
0123120