Prof. Dr. Özcan Kalenderli
7
SAYISAL YÖNTEMLER
SAYISAL İNTEGRASYON YÖNTEMLERİ
Sayısal integrasyon veya integral alma işlemi, analitik olarak bir integralin alınmasının çok zor
veya olanaksız olduğu durumlarda veya bir işlevin değerlerinin sadece belirli noktalarda
bilinmesi durumlarında önem kazanır. Ayrıca integrasyon işlemlerini içeren veya gerektiren
problemlerin bilgisayarla çözümünde kullanılan programlarda sayısal integrasyon yöntemlerinin
kullanılması kaçınılmazdır. Gerçekte analitik integral, sayısal integrale göre çözülebilme
kolaylığı ve sonucunun kesinliği ile üstünlük gösterir. Uzunluk, alan, hacim, enerji, ... gibi
pekçok büyüklüğün hesabında tek ve çok katlı integrasyondan yararlanılır. Bu bölümde bu gibi
amaçlar için kullanılabilecek tek ve çok katlı belirli integrallerin sayısal çözüm yöntemleri
açıklanmıştır.
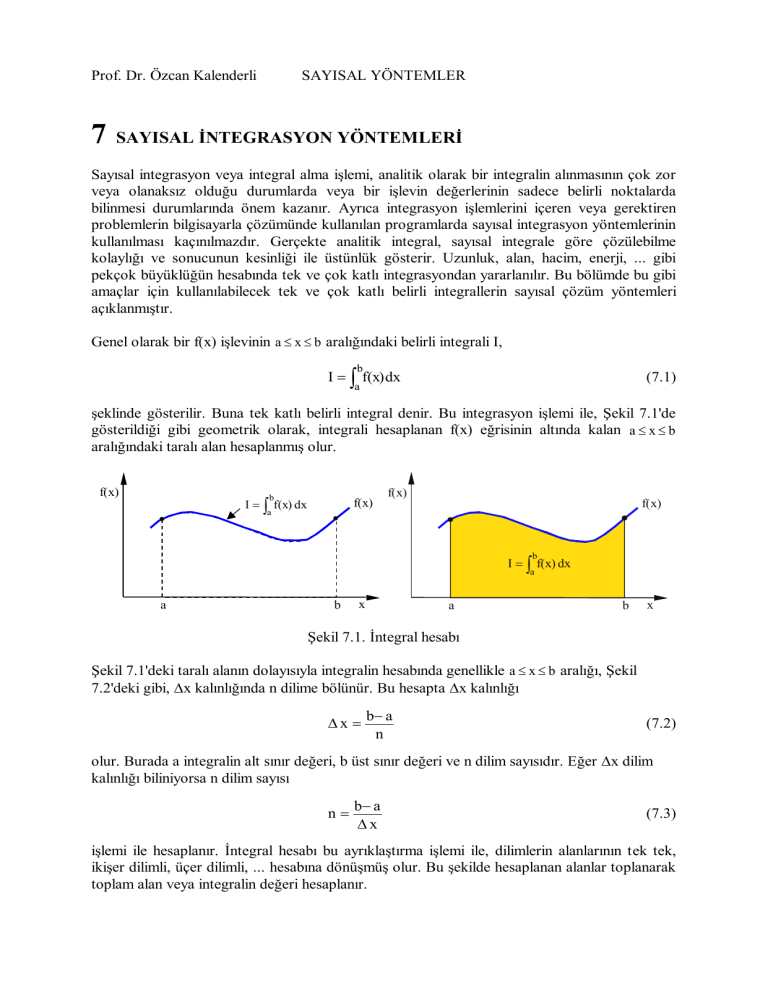
Genel olarak bir f(x) işlevinin a x b aralığındaki belirli integrali I,
b
I f(x) dx
(7.1)
a
şeklinde gösterilir. Buna tek katlı belirli integral denir. Bu integrasyon işlemi ile, Şekil 7.1'de
gösterildiği gibi geometrik olarak, integrali hesaplanan f(x) eğrisinin altında kalan a x b
aralığındaki taralı alan hesaplanmış olur.
f(x)
b
I f(x) dx
f(x)
a
f(x)
f(x)
b
I f(x) dx
a
a
b
x
a
b
x
Şekil 7.1. İntegral hesabı
Şekil 7.1'deki taralı alanın dolayısıyla integralin hesabında genellikle a x b aralığı, Şekil
7.2'deki gibi, x kalınlığında n dilime bölünür. Bu hesapta x kalınlığı
x
b a
n
(7.2)
olur. Burada a integralin alt sınır değeri, b üst sınır değeri ve n dilim sayısıdır. Eğer x dilim
kalınlığı biliniyorsa n dilim sayısı
n
b a
x
(7.3)
işlemi ile hesaplanır. İntegral hesabı bu ayrıklaştırma işlemi ile, dilimlerin alanlarının tek tek,
ikişer dilimli, üçer dilimli, ... hesabına dönüşmüş olur. Bu şekilde hesaplanan alanlar toplanarak
toplam alan veya integralin değeri hesaplanır.
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
2
f(x)
f(x)
x
a
b
x
Şekil 7.2. İntegral hesabında dilimleme (ayrıklaştırma)
Dilimlerin alanlarının veya integralin hesabında bir nokta, iki nokta, üç nokta ve dört nokta
yaklaşımları yaygın olarak kullanılan yaklaşımlardır.
7.1. Bir Nokta Yaklaşımı (Dikdörtgen Yöntemi)
Bir nokta yaklaşımında veya dikdörtgen yönteminde, Şekil 7.3'ten de görüleceği gibi, x = a için
f(a) noktasından x eksenine paralel doğru çizilerek birinci dikdörtgen dilim elde edilir. x = a +
x için f(a + x) noktasından da x eksenine paralel doğru çizilerek ikinci dikdörtgen dilim elde
edilir. Bu şekilde devam edilerek her noktadan x eksenine paralel doğrular çizilir ve dikdörtgen
dilimler elde edilir. İntegralin değeri, bu dikdörtgen dilimlerin alanlarının toplamına yaklaşık
eşittir.
f(x)
f(x)
f(xj)
x
a
b
x
Şekil 7.3. Bir nokta yaklaşımı (dikdörtgen yöntemi)
x
xj xj+1
Dikdörtgen
Sj = xj.f(xj)
Eğer dilimler farklı x kalınlıklarında ise integral
b
n
n
I f(x) dx x j f(x j) S j
a
j1
(7.4)
j1
olur. Genelde dilimler eşit x kalınlıklarında olur. Bu durumda integral
b
n
I f(x) dx x f(x j)
a
j1
olur. Bu denklemde n dilim sayısı, x = (b - a)/n dir.
(7.5)
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
3
7.2. İki Nokta Yaklaşımı (Yamuk (Trapez) Yöntemi)
Yamuk yöntemi olarak tanınan iki nokta yaklaşımında birbiri ardından gelen her iki nokta bir
doğru ile birleştirilerek Şekil 7.4'teki gibi yamuk şekilli dilimler elde edilir. Böylece integral,
yamukların alanlarının toplamına dönüştürülmüş olur.
f(xj+1)
f(x)
f(x)
x
a
b
f(xj)
x
xj xj+1
Yamuk
x
Sj = (x/2). [f(xj)+ f(xj+1)]
Şekil 7.4. İki nokta yaklaşımı (yamuk yöntemi)
Yamuğun alanı, paralel kenarlarının uzunluklarının toplamının bu iki kenar arasındaki uzaklığın
yarısı ile çarpımına eşittir. Şekil 7.5'te, yamuk yöntemi integrasyon bağıntısını elde etmek için
Şekil 7.4'ten iki dilim ayrı olarak büyütülerek yeniden çizilmiştir.
f(x)
fj-1
fj
x
xj-1
fj+1 f(x)
x
xj
x
xj+1
Şekil 7.5. İki yamuk dilimi
Şekil 7.5'ten herbir dilim için
xj
x j1 f(x) dx
x j1
x j
f(x) dx
x
(f f )
2 j1 j
x
(f f )
2 j j1
yazılır. İki dilim için
x j1
xj
x j1
x j1 f(x) dx x j1 f(x) dx x j
f(x) dx
x
x
(f j1 f j)
(f f )
2
2 j j1
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
4
x
(f 2f j f j1)
2 j1
bulunur. Bu eşitlik genelleştirilecek olursa, bir f(x) işlevinin yamuk yöntemine göre a x b
aralığındaki sayısal integrasyon eşitliği
b
I f(x) dx
a
x
f(a) 2f(a x) 2f(a 2 x) 2 f(a (n 1) x) f(b) (7.6)
2
veya
n 1
x
I f(x) dx
f(a) f(b) 2 f(a j x)
a
2
j1
b
(7.7)
elde edilir. Burada n dilim sayısıdır. Dilim kalınlığı ise
x
b a
n
olur. Genel olarak integral konusunu geometrik olarak anlamak kolay olmakla beraber,
yöntemin, sonucun doğruluğu ve bunun iyileştirilmesi için yapılması gerekenler hakkında bilgi
vermez. Ancak görüldüğü gibi, x dilim kalınlığı küçük veya n dilim sayısı büyük seçildikçe
integrasyon sonucunun doğruluğu artmaktadır.
Yamuk yönteminde yöntemin hatasını azaltmak veya doğruluğunu arttırmak için uç düzeltmesi
adı verilen işlem yapılır. Buna göre uç düzeltmeli yamuk yöntemi bağıntısı,
b
I f(x) dx
a
n 1
( x) 2
x
[f (b) f (a)]
f(a) f(b) 2 f(a j x)
2
12
j1
olur. Burada son terime uç düzeltmesi terimi denir.
Sayısal örnek 7.1:
b
I (3 x3 2 x 2 5) dx integralini x = 0,5 alarak
a
a) Yamuk ve
b) Uç düzeltmeli yamuk
yöntemleri ile hesaplayınız.
İntegrali analitik çözümü:
b
I (3 x3 2 x 2 5) dx
a
Yamuk yöntemi ile çözüm:
a = 0, b = 3, x = 0,5
3 4 2 3
x x 5x
4
3
3
0
93,75
(7.8)
Prof. Dr. Özcan Kalenderli
n
SAYISAL YÖNTEMLER
5
b a 3 0
6
x
0,5
I
615
0,5
f(0) f(3) 2 f(0 j 0,5)
2
j1
I 0,25f(0) f(3) 2[f(0,5) f(1) f(1,5) f(2) f(2,5)]
I 0,25 5 104 2[5,875 10 19,625 37 64,375] 95,6875
Hata = 95,6875 93,75 1,9375
Uç düzeltmeli yamuk yöntemi ile çözüm:
f(x) 3 x3 2 x 2 5
f' (x) 9 x 2 4 x
Iucd I
(0,5)2
3
(9 x 2 4 x 0 ) 93,75
12
Hata = 93,75 93,75 0
7.3. Üç ve Dört Nokta Yaklaşımları (Simpson Yöntemi)
7.3.1 Üç Nokta Yaklaşımı (1/3 Simpson Yöntemi)
Bu yöntemde çözüm aralığı çift sayıda n dilim sayısına bölündükten sonra herbir iki dilime
ilişkin üç noktadan geçen eğrinin altındaki alan yani integral hesaplanır. Buna göre 1/3 Simpson
kuralı veya iki dilim için Simpson kuralı
Ij
X j1
x j1
1
f(x) dx x (f j14 f j f j1)
3
(7.9)
yazılır. Genel olarak 1/3 Simpson integrasyon bağıntısı veya diğer bilinen adıyla ikişer dilimli
integrasyon bağıntısı
I
b
a
n 1
n 2
x
f(x) dx
f(a) f(b) 4 f(a j x) 2 f(a j x)
3
j1
j 2
j tek
j çift
(7.10)
olur. Burada da
x
b a
n
(7.11)
olup integral aralığı çift sayıda dilime bölünmüş olmalıdır, yani n dilim sayısı çift sayı olmalıdır.
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
6
Sayısal örnek 7.2:
I
/ 4
0
sin 2x
dx integralini 1/3 Simpson yöntemi ile n = 8 alarak hesaplayınız.
cos 2x
0
b a 4
a = 0, b = /4, x
n
8
32
81
8 2
/ 32
I
f(0) f( / 4) 4 f(0 j ) 2 f(0 j )
3
32
32
j1
j 2
j tek
j çift
I
sin 2 ( / 32) sin 2 (3 / 32) sin 2 (5 / 32) sin 2 (7 / 32)
f(0) f( / 4) 4
2
2
2
2
96
cos
(
/
32)
cos
(3
/
32)
cos
(5
/
32)
cos
(7
/
32)
sin 2 (2 / 32) sin 2 (4 / 32) sin 2 (6 / 32)
2
2
2
2
cos
(2
/
32)
cos
(4
/
32)
cos
(6
/
32)
0 1 4 (0,00970 0,09202 0,28570 0,67351) 2 (0,03956 0,17157 0,44646)
96
I
I 0,21464
İntegralin analitik değeri: I
/ 4
0
=
/ 4
/ 4
sin 2 x
dx tan 2 x dx (sec 2 1) dx
2
0
0
cos x
/ 4
0
sec 2 x dx
/ 4
0
/ 4
x dx tan x x 0
0,21460
Hata = 0,21460 0,21464 0,00004
Sayısal örnek 7.3:
3
I ex dx integralini 1/3 Simpson yöntemi ile x = 0,5 ve x = 0,25 alarak hesaplayınız.
0
a = 0, b = 3, x = 0,5 için
n
b a 3 0
6
x
0,5
I
0,5
f(0) f(3) 4[f(0,5) f(1,5) f(2,5)] 2[f(1,0) f(2,0)] 19,092
3
3
İntegralin analitik değeri, I = ex e3 1 19,08554
0
Hata = 19,092 19,08554 0,00646
a = 0, b = 3, x = 0,5 için
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
n
I
7
b a 3 0
12
x
0,25
0,5
f(0) f(3) 4[f(0,25) f(0,75) f(1,25) f(1,75) f(2,25) f(2,75)]
3
2[f(0,5) f(1,0) f(1,5) f(2,0) f(2,5)] 19,086
3
İntegralin analitik değeri, I = ex e3 1 19,08554
0
Hata = 19,086 19,08554 0,00046
7.3.2 Dört Nokta Yaklaşımı (3/8 Simpson Yöntemi)
Bu yöntemde çözüm aralığı üç ve üçün katı sayıda n dilim sayısına bölündükten sonra herbir üç
dilime ilişkin dört noktadan geçen eğrinin altındaki alan yani integral hesaplanır. Buna göre 3/8
Simpson kuralı veya üçer dilim için Simpson kuralı
Ij
X j 2
x j1
3
f(x) dx x (f j1 3 f j 3 f j1 f j2 )
8
(7.12)
yazılır. Genel olarak 3/8 Simpson integrasyon bağıntısı veya diğer bilinen adıyla üçer dilimli
integrasyon bağıntısı
I
b
a
n 1
n 3
3
f(x) dx x f(a) f(b) 3 f(a j x) 2 f(a j x)
8
j1
j3
j1,2,4,5,7,8,...
j3,6,9,...
(7.13)
olur.
f x p x ax 3 bx 2 cx d
3
2
3
3
3
3
x j1 x f j1 f x j1 p x j1 a x b x c x d
2
2
2
2
3
2
1
1
1
1
x j x f j f x j p x j a x b x c x d
2
2
2
2
3
2
1
1
1
1
x j1 x f j1 f x j1 p x j1 a x b x c x d
2
2
2
2
3
x j 2
2
3
3
3
3
x f j 2 f x j 2 p x j 2 a x b x c x d
2
2
2
2
Prof. Dr. Özcan Kalenderli
3
x j2 x
2
p x dx
3
x j1 x
2
SAYISAL YÖNTEMLER
3
x j2 x
2
ax
3
3
x j1 x
2
8
3
x j2 x
2
1
1
1
bx 2 cx d dx ax 4 bx 3 cx 2 dx
3
2
4
x j1 3 x
2
b
d
1
4 x
2
f
j1
9
b x 3 3d x
4
f j f j1 f j 2
1
f j1 9f j 9f j1 f j2
16
3
I j x f j1 3f j 3f j1 f j 2
8
n 1
n 3
3
I f x dx x f a f b 3 f a j x 2 f a j x
8
j1
j 3
a
1,2,4,5,
3,6,9,
b
Sayısal örnek 7.4:
I
3
1
x 2
dx integralini 3/8 Simpson yöntemi ile n = 9 alarak hesaplayınız.
2 x 3
a = -1, b = 3, x
b a 3 (1) 4
0,4444
n
9
9
91
93
3
I 0,4444f(1) f(3) 3 f(1 j 0,4444) 2 f(1 j 0,4444)
8
j1
j3
j1, 2, 4, 5, ...
j3, 6, ...
3
I 0,4444f(1) f(3) 3(f(0,5556) f(0,1112) f(0,7776) f(1,2222)
8
f(2,1108) f(2,5552)) 2(f(0,3332) f(1,6664))
I 5,334299
İntegralin analitik değeri = 5,333333
Hata = 5,333333 5,334299 0,000966
7.4. Çok Katlı İntegrasyon
Çok katlı integrasyonda her kat bilinen bir sayısal integrasyon yöntemi ile hesaplanarak tüm
integral hesaplanır. Örneğin iki katlı bir integral
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
I
9
d b
f(x, y) dx dy
(7.14)
c a
ise burada
b
g(y) f(x, y) dx
(7.15)
a
iç veya birinci kat integral olur. Dolayısıyla tüm integralin sonucu
d
I g(y) dy
(7.16)
c
integralinin hesabından bulunur. Örneğin böyle bir integralin çözümü dikdörtgen yöntemi ile
yapılacak olursa
d b
d
c a
c
I
n
d
m
f(x, y) dx dy ( f(xi , y) x) dy g(y) dy g(y j) y (7.17)
c
i 1
j1
işlemi yapılır.
Örnek 7.5:
Şekil 7.6 için I
d b
f(x, y) dx dy integralini yamuk yöntemi ile çözünüz.
c a
b
d
a
c
g(y) f(x, y) dx ve I g(y) dy işlemi yapılacaktır. Buna göre
g(y)
d
x
f(a, y) f(b, y) 2[f(a x, y) f(a 2 x, y)]
2
y x
f(a, c) f(b, c) 2[f(a x, c) f(a 2 x, c)]
2 2
f(a, d) f(b, d) 2[f(a x, d) f(a 2 x, d)]
2[f(a, c y) f(b, c y) f(a x, c y) f(a 2 x, c y)]
I g(y) dy
c
y
d
y
y
c
x
x
a
x
b
Şekil 7.6.
x
Prof. Dr. Özcan Kalenderli
SAYISAL YÖNTEMLER
10
Sayısal örnek 7.6:
I
3 2
1 1
x y (1 x) dx dy integralini yamuk yöntemi ile
x
b a 2 1 1
0,3
n
3
3
y
d c 3 1
1
m
2
alarak hesaplayınız.
Bir önceki örnekteki gibi çözümle
d
y x
f(a, c) f(b, c) 2[f(a x, c) f(a 2 x, c)]
2 2
f(a, d) f(b, d) 2[f(a x, d) f(a 2 x, d)]
2[f(a, c y) f(b, c y) f(a x, c y) f(a 2 x, c y)]
I g(y) dy
c
bağıntısı oluşturulursa
I
1 0, 3
f(1,1) f(2,1) 2[f(1 0, 3 ;1) f(1 2.0, 3 ;1)]
2 2
f(1, 3) f(2, 3) 2[f(1 0, 3 ; 3) f(1 2.0, 3 ; 3)]
2[f(1; 1 1) f(2; 1 1) f(1 0, 3 ; 1 1) f(1 2.0, 3 ; 1 1)]
I = 15,340
İntegralin analitik değeri = 15,333
Hata = 15,333 15,340 0,007