LYS LYS L M T

LYS
LİMİT
Matematik1
Matematik
SAĞDAN VE SOLDAN YAKLAŞMA
x
Yandaki tabloda bir x değişkeninin 4 sayısına sağdan ve soldan
4
Soldan yaklaflma
yaklaşımı ifade edilmiştir. Bu durumu genellemek gerekirse;
x değişkeni a reel sayısına, a dan küçük değerlerle yaklaşıyorsa,
bu tür yaklaşmaya soldan yaklaşma denir ve x → a– şeklinde
gösterilir.
x
Sa¤dan yaklaflma
x
x
3
5
3,5
4,5
3,9
4,1
x değişkeni a reel sayısına, a dan büyük değerlerle yaklaşıyorsa,
3,99
4,01
bu tür yaklaşmaya sağdan yaklaşma denir ve x → a+ şeklinde
3,999
4,001
gösterilir.
.......
.......
x → 4–
x → 4+
x in –2 ye soldan yaklaşması hangisi ile ifade
x in –2 ye sağdan yaklaşması hangisi ile ifade
edilir?
edilir?
SAĞDAN LİMİT VE SOLDAN LİMİT
x değişkeni a ya soldan yaklaştığında (x → a–) f(x) fonksiyonu da L1 reel sayısına yaklaşıyorsa
“f(x) in x = a daki soldan limiti L1 dir.” denir ve lim f(x) = L1 şeklinde gösterilir.
x " a–
+
x değişkeni a ya sağdan yaklaştığında (x → a ) f(x) fonksiyonu da L2 reel sayısına yaklaşıyorsa
“f(x) in x = a daki sağdan limiti L2 dir.” denir ve lim f(x) = L2 şeklinde gösterilir.
x " a+
Soldan limit, sağdan limite eşit ise fonksiyonun limiti vardır. Farklı ise fonksiyonun limiti yoktur.
lim f(x) = lim f(x) = L ise lim f(x) = L dir.
x " a–
x " a+
x"a
lim f(x) ≠ lim f(x) ise lim f(x) yoktur.
x " a–
x " a+
x"a
Aşağıda grafiği verilen fonksiyonların x=a noktasındaki limitlerini inceleyelim.
y
y
f(x)
L
0
L2
L2
L1
L
L1
x
a
y
f(x)
0
y
0
f(x)
L
f(x)
0
0
x
a
y
y
f(x)
x
a
f(x)
a
a
x
0
a
x
x
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
Aşağıda grafiği verilen fonksiyonların x=a noktasındaki limitlerini inceleyelim.
y
y
f(x)
0
x
a
0
a
x
f(x)
Aralığın uç noktalarındaki limit değerini bulmak
y
için sağdan veya soldan limite bakmak yeterlidir.
y
a
L1
0
L2
0
f(x)
3
2
a1
x
a2
x
c
b
–4
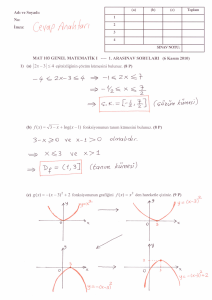
Yukar›da f(x) fonksiyonunun grafi¤i verilmifltir.
Buna göre,
y
y
4
3
3
1
–3
3/2
–1 O
–2
3
2
3
y=f(x)
x
–3 –1
y=g(x)
lim f(x) + lim f(x) + lim f(x)
x →a +
x →c +
toplam› kaçt›r?
2
1
O
x →b −
3
x
A) –2
B) –1
C) 0
D) 1
E) 3
2008 – ÖSS
–2
Grafiği verilen y = f(x) ve y = g(x) fonksiyonlarına
göre, aşağıdaki soruları cevaplayınız.
1.
lim f (x)
B
x"3
y
2.
3
lim f (x)
2
x "−3
3
3.
–3
lim (f (x) + g (x))
–1
x"3
y = f(x)
–3
4.
lim (f − g) (x)
y = f(x) in grafiği verilmiştir.
x "−3
lim
x " –1
5.
x
0
lim (fog) (x)
x " 0–
f 3 (x) + f (x + 1)
limitinin eşiti nedir?
(fof) (x)
A) –8
B) –9
C) –
28
3
D) –
29
3
E) –10
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
Aşağıda grafiği verilen fonksiyonların x= ∞ ve – ∞ noktasındaki limit değerlerini inceleyelim.
y
y
y
f(x)
b
f(x)
b
0
x
0
x
b
x
0
f(x)
y
2
2
–2
–1 0
4
5
x
6
Yukarıda grafiği verilen y=f(x) fonksiyonunun x in –4, –3,
–2, –1, 0, 1, 2 değerleri için limitlerini araştırınız.
–2
Yukarıda grafiği verilen y = f(x) fonk siyonunun
grafiğine göre, aşağıdakilerin değerlerini bulunuz.
lim f(x)
lim f(x)
x"0
x"5
lim f(x)
lim f(x)
x"2
x"6
y
y=f(x)
3
2
–5
1
–4
O
x
1
Grafiği verilen f(x) fonksiyonunun [–6, 3) aralığında apsisi tam sayı olan kaç noktada limiti vardır?
A)8
B)7
C)6
D)5
E)4
A
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
Polinom Fonksiyonların Limitleri
n
n–1
f(x)=anx +an–1x +...+aa şeklindeki fonksiyonlara polinom fonksiyon denir ve bütün reel sayılar için tanımlıdır. Yani, bu biçimdeki
fonksiyonları tanımsız yapan değerler yoktur ve grafikleri kesintisiz bir eğri şeklindedir.
Grafikleri kesintisiz olduğundan dolayı bu fonksiyonlarda herhangi bir noktada limit alınırken sağdan ve soldan limite bakmaya
gerek yoktur. Sadece fonksiyonun o noktadaki değerinin bulunması yeterlidir. lim f(x) = f(a) dır.
x →a
lim ( 2 x 2 − x + 1) limitinin değeri kaçtır?
lim ( − x 3 − x − 10 ) limitinin değeri kaçtır?
x →−1
A) 4
x →−2
B) 5
C) 6
D) 7
E) 8
A) –6
B) –4
C) –2
D) 0
E) 2
D
A
f(x)
,
g(x)
h(x) , logk(x) biçimindeki kesirli, köklü ve logaritmik fonksiyonların tanımlı olduğu yerler sırasıyla g(x)≠0, h(x)≥0 ve k(x)>0
f(x) f(a)
=
, lim h(x)
şartını sağlayan aralıklardır. Bu aralıklardaki a reel sayıları için=
limit lim
x→a g(x) g(a)
x→a
h(a)=
ve lim log k(x) log k(a)
x→a
biçiminde hesaplanır. Bu aralıklar dışında fonksiyonların tanımsız olduğu yerlerde ise sağdan ve soldan limit incelemesi yapılmalıdır. İlerleyen bölümlerde bu noktalardaki limitler ayrıca incelenecektir.
lim
x →1
A) 1
lim log3 ( 7 x + 2 ) limitinin değeri kaçtır?
x+3
limitinin değeri kaçtır?
2x − 1
B) 2
C) 3
x →1
D) 4
E) 5
A) 1
B) 2
C) 3
D) 4
E) 5
B
B
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
Parçalı Fonksiyonların Limitleri
f(x)=
g(x) ,
x<a
h(x) ,
x≥a
biçimindeki parçalı fonksiyonlarda fonksiyonun kritik noktası x=a dır. Parçalı fonksiyonların grafikleri incelendiğinde kritik noktalarında kesintiler (sıçramalar) olabildiği görülür. Bundan dolayı kritik noktalarda sağdan ve soldan limit incelemesi yapılması gerekir.
Kritik nokta dışındaki limit incelemelerinde ise uygun olan fonksiyon seçilerek (g(x) veya h(x)) limit alınmaya çalışılır.
Not: Parçalı fonksiyonlarda limit incelemesi yapmak için grafik çizilmesi şart değildir.
ax + b,
x≥3
⎪
f(x) = ⎨ 10,
1< x < 3
⎪2x + a – b, x ≤ 1
⎩
⎧5x – 2, x ≥ 2
f(x) = ⎨
⎩3x + 2, x < 2
olduðuna göre, lim f(x) deðeri kaçtýr?
x→2
A) 8
B) 5
C) 2
D) 0
Yukarýda verilen f(x) fonksiyonunun tüm reel sayýlar
için limiti olduðuna göre, b kaçtýr?
E) Yoktur
A) – 4
B) –
7
2
C) –
1
2
D) 4
E)
9
2
A
⎧ x2 – 1
, x >1
⎪
⎪⎪ x – 1
f(x) = ⎨ 3,
x =1
⎪ k,
x <1
⎪
⎪⎩
B
⎪⎧ x 2 – 2, x > n
f(x) = ⎨
⎪⎩ 3x + 2, x ≤ n
lim f(x) bir reel sayý olduðuna göre, k kaçtýr?
x →1
A) 6
B) 5
C) 4
D) 3
lim f(x) bir reel sayýya eþit ve lim f(x) = – 2 olduðuna
E) 2
x →n
x →0
göre, n kaçtýr?
A) – 2
B) – 1
C) 0
D) 2
E) 4
B
E
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
Mutlak Değerli Fonksiyonların Limitleri
Mutlak değerli fonksiyonların kritik noktası ifadeyi 0 yapan değerlerdir. Kritik noktalarda limit araştırılırken sağdan ve soldan limit
incelemesi yapılmalıdır. Kritik olmayan noktalarda ise limit değeri fonksiyonu o noktadaki değerdir. Yani lim f(x) = f(a) dir.
x →a
lim
x→2
x–1 + x+1
lim
x → 3–
deðeri kaçtýr?
de¤eri kaçt›r?
A) 1
B) 2
| x 3 – 27|
x 4 – 81
C) 3
D) 4
E) 5
A) – 3
B) – 1
C) –
1
4
D) 0
E) 3
D
x–2
x–2
lim
x→2
C
iflleminin sonucu kaçt›r?
A) –1
B) 0
C) 1
D) ∞
E) Limit yoktur.
lim
x → 2–
| x 2 – 5x + 6|
x–2
deðeri kaçtýr?
A) – 2
B) – 1
C) 0
D) 1
E) 2
B
E
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
Genişletilmiş Gerçek Sayılar Kümesinde Limit
Herhangi bir x değişkeni sürekli artan değerler alıyorsa x → ∞, x değişkeni sürekli azalan değerler alıyorsa x → – ∞ ile ifade edilir.
– ∞ ile + ∞ kavramlarının reel (gerçek) sayılar kümesine eklemesiyle oluşan R ∪ {– ∞, + ∞} kümesine genişletilmiş gerçek sayılar
kümesi denir.
g(a)=0 olmak üzere lim
x →a
ifadesinde soldan ve sağdan limit incelemesi yapılmalıdır.
g(x)
lim 1
x
lim x + 1
x
x→0+
lim x →3
x→0–
1
x – 3


lim  x + 2 
x – 2
x→2
lim
x®a
f(x)
ifasinde x=a değeri, g(x)=0 denkleminin çift katlı bir kökü ise aşağıda belirtilen durumlar geçerlidir.
g(x)
lim x + 32
(x – 1)
lim 32
x
x→0
x→1
Sonsuz kavramı ile ilgili bazı özellikler aşağıdadır.

c ∈ R olmak üzere, c+(+∞)=+∞
c+(–∞)=–∞

c > 0 olmak üzere
c.(+∞)=+∞
c.(–∞)=–∞
c < 0 olmak üzere
c.(+∞)=–∞
c.(–∞)=+∞

∞+∞=∞

–∞+(–∞)=–∞

∞.∞=∞
,
(–∞).(–∞)=∞
ve
(+∞).(–∞)=– ∞ dur.
lim
lim x 2 – 1
x → –∞
x→∞
n
n–1
f(x)=anx +an-1x
+.....+a1x+a0 biçimindeki polinom fonksiyonlar için
terimin limitini almak yeterlidir.
lim
x → –∞
x+1
x–1
3
lim f(x) limiti hesaplanırken sadece en büyük dereceli
x ®±¥
lim f(x) = lim an xn
x ®±¥
x2 – x + 1
x ®±¥
lim
x → –∞
4x2 + 1
LYS
Matematik
LYS
LİMİT
Matematik1
Matematik
lim a x biçimindeki limitleri hesaplamak için aşağıdaki örnekleri inceleyelim.
x ®±¥
lim a x = 0
a > 1 ise lim a x = ¥
a > 1 ise
0 < a < 1 ise lim a x = 0
0 < a < 1 ise
x ®¥
x ®¥
x ®-¥
lim a x = ¥
x ®-¥
5
lim  
x →∞  7 
lim 4 x
x →−∞
x
2
lim  
x →−∞  3 
x
x=logax biçimindeki limitleri hesaplamak için y=logax fonksiyonunun aşağıdaki grafiklerini dikkatle inceleyelim.
lim (log5 x )
x → 0+
lim (log x )
x →∞
1
 1  x −1
lim  
−  2 
x →1
lim
x→e
−
x
3ln x − 3
lim (log 1 x )
x → 0+
3
lim (log 1 x )
x →∞
7
1
lim 10 x − 2
x → 2+
lim
x→e
−
1
1 − ln x
LYS
Matematik