ÖZEL EGE LİSESİ OKULLAR ARASI 9.MATEMATİK YARIŞMASI 10

ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL SORULARI
− 4 − 9x2
< 0 eşitsizliğinin sağlanması için ; a nın bulunduğu
x 2 + 4ax − 4a + 2
en geniş reel sayı aralığını bulunuz.
1) ∀x ∈ R için,
2) Tepe noktası T(3,8) olan parabol ile y=x-1 doğrusunun teğet olabilmesi için, bu
parabol fonksiyonunun katsayılar toplamını bulunuz.
3.) x, y, z pozitif reel sayılardır.
1 3 4
+ + = 16 ise x.y 3 .z 4 çarpımının en küçük
x y z
değerini bulunuz.
4) ∀ n ∈ Z + için; 5 12n − 3 12n ifadesinin 28 ile bölünebileceğini gösteriniz.
4b2 + a2
= 0 ikinci derece denkleminin köklerinden biri -2 ise a.b
4
çarpımının değerini bulunuz.
5) x 2 + 2 ab .x +
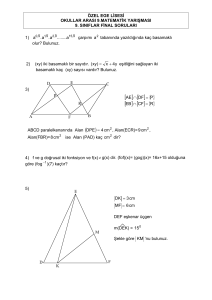
6)
E
A
B
F
.
D
Yukarıdaki verilere göre;
ABCD paralelkenar ,
[DE] ⊥ [FC],
DA = DF = FC
EA = EB veriliyor.
C
AB
DE
oranını ve DAE nın ölçüsünü bulunuz.
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL SORULARI
7) Hileli bir zarda herhangi bir sayının üst yüzde gelme olasılığı , bu sayının 3 katı ile
5
orantılıdır. Hileli bir parada yazı gelme olasılığı
dır. Bu para ve zar bir kez beraber
6
atıldığında zarın üst yüzünde tek sayı veya paranın tura gelme olasılığını bulunuz.
8) Bir ABC üçgeninin çevrel çemberini A, B, C açılarına ait iç açıortay doğruları
sırasıyla P, Q, R noktalarında kesiyor. [AP] ⊥ [RQ] olduğunu gösteriniz.
9)
y
B( 4,7)
A(1,5)
0
C( x,0)
x
ABC üçgeninin çevresi en küçük değer aldığında alanının kaç br 2 olduğunu bulunuz.
1 1 1
1
+ + =
x y z x+y+z
ispatlayınız.
10)
ise ve n tek sayı için;
1
1 1
1
+ n+ n= n
olduğunu
n
x
y
z
x + yn + zn
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL CEVAPLARI
− 4 − 9x2
< 0 eşitsizliğinin sağlanması için ; a nın bulunduğu
x 2 + 4ax − 4a + 2
en geniş reel sayı aralığını bulunuz.
ÇÖZÜM:
− 4 − 9x2
< 0 ise x 2 + 4ax − 4a + 2 >0 olmalıdır. Bunun için ∆ <0
2
x + 4ax − 4a + 2
olmalıdır..Öyleyse 16a2 − 4( −4a + 2) <0 ise 16a2 + 16a − 8 < 0 ise 2a2 + 2a − 1 < 0
olmalıdır. ∆=4-4.(-1).2=12 ve
− 2 − 2 3 − 1− 3
− 2 + 2 3 − 1+ 3
=
=
bulunur.
a1 =
, a2 =
4
2
4
2
1) ∀x ∈ R için,
− 1+ 3
2
− 1− 3
2
Öyleyse çözüm kümesi
2a + 2a − 1
2
+
−
+
(
− 1− 3 − 1+ 3
,
) dir.
2
2
2) Tepe noktası T(3,8) olan parabol ile y=x-1 doğrusunun teğet olabilmesi için, bu
parabol fonksiyonunun katsayılar toplamını bulunuz.
ÇÖZÜM:
−b
Parabolün denklemi ax 2 + bx + c = y olsun. T(r,k) için r=
=3 ise b=-6a olur.
2a
f(3)=8 ise 9a+3b+c=8 , 9a+-18a+c=8 ise c=8+9a dır.
O halde parabol y= ax 2 + ( −6a)x + 9a + 8 olur.
Teğet ise x-1= ax 2 + ( −6a)x + 9a + 8
0= ax 2 + ( −6a − 1)x + 9a + 9 ise ∆=0 olmalı .
( −6a − 1) 2 − 4a(9a + 9) = 0
1
6
49
9
a=
bulunur. Buna göre b=, c=
dır.
+ 8 dir. Öyleyse a+b+c=
24
24
6
24
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL CEVAPLARI
3) x, y, z pozitif reel sayılardır.
1 3 4
+ + = 16 ise x.y 3 .z 4 çarpımının en küçük
x y z
değerini bulunuz.
ÇÖZÜM:
Aritmetik ortalama geometrik ortalamadan büyük veya eşit ise
1 1 1 1 1 1 1 1
+ + + + + + +
1 1 1 1 1 1 1 1
x y y y z z z z
≥8 . . . . . . .
8
x y y y z z z z
16
1 1 1
≥8 . 3. 4
8
x y z
2≥8
1 1 1
. .
x y3 z4
1
1
dır.
≤ xy 3 z 4 bulunur. Öyleyse en küçük
256
256
4) ∀ n ∈ Z + için; 5 12n − 3 12n ifadesinin 28 ile bölünebileceğini gösteriniz.
ÇÖZÜM:
5 12n − 3 12n ifadesi 28 ile bölünebiliyorsa 4 ve 7 e de bölünür.
5 12n − 3 12n ≡ (1)12n − (− 1)
12n
( )
3 4n
( )
≡ 1 − 1 ≡ 0 (mod 4 ) doğrudur.
3 4n
512n − 312n ≡ 5
− 3
≡ 6 4n − 6 4n ≡ 0 (mod 7) doğrudur.
Öyleyse 5 12n − 3 12n ifadesi 28 ile bölünebilir.
4b2 + a2
= 0 ikinci derece denkleminin köklerinden biri -2 ise a.b
4
çarpımının değerini bulunuz.
5) x 2 + 2 ab .x +
ÇÖZÜM:
4b2 + a2
x + 2 ab .x +
= 0 ise ∆ ≥ 0 olmalıdır. Öyleyse
4
4b 2 + a 2
2
4ab-4(
) ≥ 0 ise − (2b - a ) ≥ 0 ise 2b-a=0 ise 2b=a dır.
4
x=-2 için 4 − 4 2 .b + 2b 2 = 0 olur
2
b2 − 2 2 b + 2 = 0
(
b>0 için b − 2
)
2
=0
b= 2
Öyleyse a.b= 4 olur.
b2 + 2 2 b + 2 = 0
(
b<0 için b + 2
)
2
b=− 2
=0
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL CEVAPLARI
6)
E
A
ABCD paralelkenar ,
[DE] ⊥ [FC],
DA = DF = FC
B
F
.
EA = EB veriliyor.
C
D
Yukarıdaki verilere göre;
AB
oranını ve DAE nın ölçüsünü bulunuz.
DE
ÇÖZÜM:
30o
2y
2y E
A
F
.
2y
2y
B
2y
2y
o
30
60o
45o
D
2y
45o
2 2y
C
K
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL CEVAPLARI
DF = FC = 2y , DC = 2y 2 , AE = EB = y 2
KEB~KDC ve
EB
DC
=
KB
KC
KFC dik üçgeninde FC =
2 2
3 +1
= 6− 2=
AB
=
1
2
KC
2
o halde K açısının ölçüsü 30 0 olur.
dir.
DE
7) Hileli bir zarda herhangi bir sayının üst yüzde gelme olasılığı , bu sayının 3 katı ile
5
orantılıdır. Hileli bir parada yazı gelme olasılığı
dır. Bu para ve zar bir kez beraber
6
atıldığında zarın üst yüzünde tek sayı veya paranın tura gelme olasılığını bulunuz.
ÇÖZÜM:
1
2
3
4
5
6
3k 6k
9k
12k 15k
18k
tek sayı olma durumu A
tura gelme olayı B
P( A ∪ B) = P( A ) + P(B) − P( A ∩ B) ise
27 1 27 1 11
. =
+ −
dir.
=
63 6 63 6 21
8) Bir ABC üçgeninin çevrel çemberini A, B, C açılarına ait iç açıortay doğruları
sırasıyla P, Q, R noktalarında kesiyor. [AP] ⊥ [RQ] olduğunu gösteriniz.
ÇÖZÜM:
A
K
R
Q
I
B
C
P
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL CEVAPLARI
m(KQI)= m(RQB)=m(RCB)=
m(Ĉ)
2
m(KIQ)=180 - m(KIB) = 180 –(180-
m( Â ) m(B̂)
)
−
2
2
m( Â ) m(B̂)
1
=
(180 – m( Ĉ ))
+
2
2
2
m(Ĉ)
= 90 2
m(IKQ)=180 – [m(KQI)+ m(KIQ)] =90 derece bulunur.
=
9)
y
B( 4,7)
A(1,5)
x
C( x,0)
0
ABC üçgeninin çevresi en küçük değer aldığında alanının kaç br 2 olduğunu bulunuz.
ÇÖZÜM:
y
y−7 x−4
9
=
ise y=0 için x=
5 + 7 4 −1
4
B( 4,7)
A(1,5)
0
1
Alan(ACB)=
P( 4,0 )
x
C( x,0)
(5 + 7).3 − ⎛ 5 .5. 1 + 7 .7. 1 ⎞ = 35 br 2
2
⎜
⎝4
2
4
⎟
2⎠
4
ÖZEL EGE LİSESİ
OKULLAR ARASI 9.MATEMATİK YARIŞMASI
10. SINIFLAR FİNAL CEVAPLARI
1 1 1
1
+ + =
x y z x+y+z
ispatlayınız.
ÇÖZÜM:
10)
ise ve n tek sayı için;
1
1 1
1
+ n+ n= n
olduğunu
n
x
y
z
x + yn + zn
x ≠ 0 , y ≠ 0 , z ≠ 0 ve x+y+z ≠ 0 olmak üzere
1 1 1
1
+ + =
x y z x+y+z
1 1
1
1
+ =
−
x y x+y+z z
x+y
− (x + y)
=
x.y
z.( x + y + z)
z.(x+y)(x+y+z) = -x.y.(x+y)
z.(x+y)(x+y+z) +x.y.(x+y) = 0
(x+y)[z.(x+y+z)+x.y]=0
(x+y).[x.z+y.z+z 2 +x.y]=0
(x+y)(x+z)(y+z)=0
x=-y veya y=-z veya x=-z
x=-y ise x+y+z =-y+y+z
x+y+z =z
1
1
x n = -y n (n tek ise) öyle ise n = − n
x
y
1
1 1
1
1
1
+ n+ n= n
eşitliğinde n = n kalır.. Diğer iki durum için de eşitliğin
n
n
n
x
y
z
x +y +z
z
z
sağlandığı görülür.