PowerPoint Sunusu - Kocaeli Üniversitesi

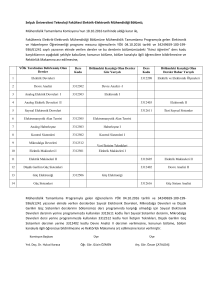
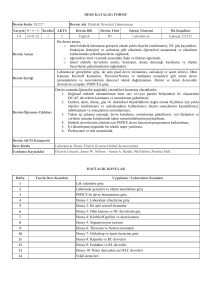
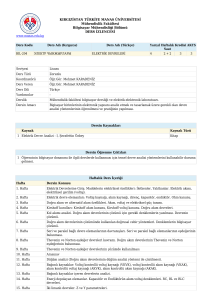
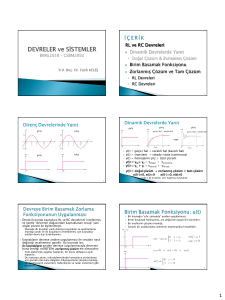
Elektrik Devre Temelleri
13
BİRİNCİ DERECEDEN DEVRELER
Doç. Dr. M. Kemal GÜLLÜ
Elektronik ve Haberleşme Mühendisliği
Kocaeli Üniversitesi
7.1. Giriş
• Bu bölümde:
– Direnç ve kapasitörden oluşan RC devreleri
– Direnç ve endüktörden oluşan RL devreleri
– Bu devrelere anahtar ile uygulanan kaynaklar incelenecektir
• Bu tip devrelere Kirchoff Kanunları uygulandığında
diferansiyel eşitlik takımları elde edilir
• Bu eşitlikleri çözmek doğrusal eşitliklere göre daha
zordur
• RL ve RC devrelerinde bulunan diferansiyel denklemler
1.dereceden olduğu için bu tip devrelere 1.Dereceden
Devreler denilir
7.1. Giriş
• RL ve RC devreleri iki ayrı durumda incelenir
– 1- Doğal Yanıt (Kaynaksız Devre)
– 2- Birim Basamak Yanıtı (Bağımsız Kaynaklı Devre)
• Kaynaklı devre analizi için 3 farklı kaynak
fonksiyonu tanımı kullanılacaktır.
a) Birim Basamak
b) Birim Darbe
c) Birim Rampa
7.2. Kaynaksız RC Devreleri
• Bir RC devresindeki DC kaynak aniden
çıkarıldığında Kaynaksız RC devresi
oluşur.
• Devredeki kapasitör, üzerinde depoladığı
enerjiyi dirence aktarmaya başlar.
• Kapasitör üzerindeki v(t) gerilimi:
– t=0 anında: v  0   V0
t>0 için A düğümüne KAK:
iC  iR  0
Birinci dereceden
dif. denklem
dv
v

0
dt RC
A
7.2. Kaynaksız RC Devreleri
dv
v

0
dt RC
Denklemde her iki tarafın integrali alındığında:
dv
1

dt
v
RC
t
ln v  
 ln A
RC
İntegral sabiti (ilk durum)
v  t   Aet / RC

Denkleme başlangıç değerleri ilave edilirse (v(0)=𝑉0 );
v  t   V0e t / RC
7.2. Kaynaksız RC Devreleri
• NOT: Bir devrenin doğal yanıtı; devrede kaynak
yokken yalnızca devre elemanlarının yanıtıdır.
Aslında devre başlangıçta depolanan kapasiteden
dolayı başlangıç değerine sahiptir.


t=τ anı gerilimin ilk değerinin
0.368 katına (1/e değerine
ulaştığı) düştüğü zamandır.
Zaman sabiti denir ve τ ile
gösterilir.
7.2. Kaynaksız RC Devreleri
• t=τ alınırsa;

Zaman sabitine göre denklemi tekrar yazarsak;
v  t   V0 e  t /


V(t) nin 𝑉0 ′nın %1’inden az
olduğu zaman 5τ’dur.
5τ zaman anı kapasitör için
kalıcı duruma geçtiği zaman
olarak kabul edilir.
7.2. Kaynaksız RC Devreleri
• Direnç üzerindeki akım:

direnç üzerindeki anlık güç:

direnç üzerindeki enerji:
7.2. Kaynaksız RC Devreleri
7.2. Kaynaksız RC Devreleri
Kaynaksız RC devrelerinde Bilinmesi Gerekenler
• 1- Kapasitör üzerindeki başlangıç gerilimi
v(0)=𝑉0
• 2- Zaman sabiti
NOT: Devrede tek bir kapasitör ve birden fazla
direnç, bağımlı kaynaklar varsa zaman sabitini
hesaplamak için gerekli 𝑅𝑒ş direnci, kapasitör
uçlarından devrenin Thevenin eşdeğeri elde
edilerek bulunur.
Örnek 7.1
• Devrede vc(0) = 15 V verilmektedir. t > 0 için vc,
vx, ix ?
Örnek 7.2
• Devredeki anahtar uzun süredir kapalı iken
t=0’da açılmaktadır. v(t) , w(0) ?
• Anahtar kapalı konumda kapasitör açık devre:
• Kapasitör üzerindeki gerilim aniden değişemeyeceğinden
Örnek 7.2
• t>0 için (anahtar açık):
7.3. Kaynaksız RL devresi
• Bu devrelerde ilgilenilen endüktör
üzerinden geçen akım ifadesidir.
• Öncelikle endüktör üzerinden başlangıçta
akan akım değeri hesaplanır.

Başlangıçta endüktörde depo edilen enerji:

t>0 için devrede KGK uygulandığında:
7.3. Kaynaksız RL devresi
i  t   I 0e  Rt / L
7.3. Kaynaksız RL devresi
• Direnç üzerindeki gerilim:

Direnç üzerindeki anlık güç:

Direnç üzerindeki harcanan enerji:

Dikkat edilirse; t → ∞ 𝑤𝑟 (∞)= 𝐿𝐼02 bu değerde 𝑤𝐿 (0) değeri ile
2
aynıdır. Endüktörün ilk anındaki enerji zamanla direnç üzerinde
harcanır.
1
7.3. Kaynaksız RL devresi
Kaynaksız RL devrelerinde Bilinmesi Gerekenler
• 1- Endüktörden geçen başlangıç akımı i(0)=𝐼0
• 2- Zaman sabiti
NOT: Daha önce de bahsedildiği gibi eğer
devrede tek bir endüktör ve birden fazla direnç,
bağımlı kaynaklar varsa zaman sabitini
hesaplamak için gerekli 𝑅𝑒ş direnci, endüktör
uçlarından devrenin Thevenin eşdeğeri elde
edilerek bulunur.
Örnek 7.3
• Devrede i(0)=10 A ise i(t) ve ix(t) ?
• 1. yol: Thevenin eşdeğeri
Örnek 7.3
• 2. yol: Doğrudan çözüm
Örnek 7.4
• Devredeki anahtar uzun süredir kapalı iken
t=0’da açılmaktadır. t>0 için i(t) ?
• Anahtar kapalı iken DC eşdeğer (t<0):
Örnek 7.4
• Anahtar açıldığında (t>0):
Örnek 7.5
• Devrede tüm zaman
aralığı için i0, v0, i ?
Örnek 7.5