emat çalışma soruları 1) ⃗ = 4. ̂ − 2. ̂

EMAT ÇALIŞMA SORULARI
�⃗ = 𝚤𝚤̂𝑥𝑥 + 4. 𝚤𝚤̂𝑦𝑦 − 4. 𝚤𝚤̂𝑧𝑧 vektörlerinin dik olduğunu gösteriniz.
1) 𝐴𝐴⃗ = 4. 𝚤𝚤̂𝑥𝑥 − 2. 𝚤𝚤̂𝑦𝑦 − 𝚤𝚤̂𝑧𝑧 ve 𝐵𝐵
ÇÖZÜM: İki vektörün skaler çarpımlarının sıfır olması gerekir.
�⃗ = 4.1 + (−2). 4 + (−1). (−4) = 0
𝐴𝐴⃗. 𝐵𝐵
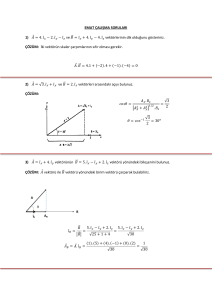
�⃗ = 2. 𝚤𝚤̂𝑥𝑥 vektörleri arasındaki açıyı bulunuz.
2) 𝐴𝐴⃗ = √3. 𝚤𝚤̂𝑥𝑥 + 𝚤𝚤̂𝑦𝑦 ve 𝐵𝐵
ÇÖZÜM:
𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 =
𝐴𝐴𝑥𝑥 . 𝐵𝐵𝑥𝑥
�𝐴𝐴𝑋𝑋2 +
1/2
𝐴𝐴2𝑦𝑦 � . 𝐵𝐵𝑥𝑥
𝜃𝜃 = 𝑐𝑐𝑐𝑐𝑐𝑐 −1
=
√3
= 30𝑜𝑜
2
√3
2
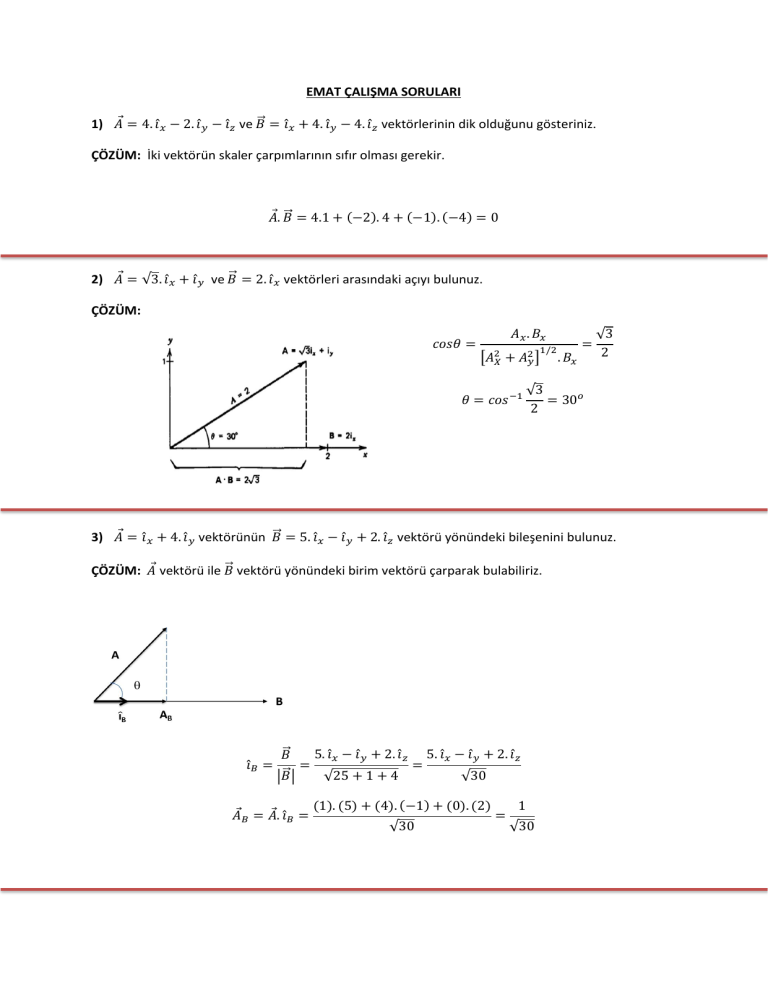
�⃗ = 5. 𝚤𝚤̂𝑥𝑥 − 𝚤𝚤̂𝑦𝑦 + 2. 𝚤𝚤̂𝑧𝑧 vektörü yönündeki bileşenini bulunuz.
3) 𝐴𝐴⃗ = 𝚤𝚤̂𝑥𝑥 + 4. 𝚤𝚤̂𝑦𝑦 vektörünün 𝐵𝐵
�⃗ vektörü yönündeki birim vektörü çarparak bulabiliriz.
ÇÖZÜM: 𝐴𝐴⃗ vektörü ile 𝐵𝐵
𝚤𝚤̂𝐵𝐵 =
�⃗
5. 𝚤𝚤̂𝑥𝑥 − 𝚤𝚤̂𝑦𝑦 + 2. 𝚤𝚤̂𝑧𝑧 5. 𝚤𝚤̂𝑥𝑥 − 𝚤𝚤̂𝑦𝑦 + 2. 𝚤𝚤̂𝑧𝑧
𝐵𝐵
=
=
�⃗�
�𝐵𝐵
√25 + 1 + 4
√30
𝐴𝐴⃗𝐵𝐵 = 𝐴𝐴⃗. 𝚤𝚤̂𝐵𝐵 =
(1). (5) + (4). (−1) + (0). (2)
√30
=
1
√30
�⃗ ve 𝐶𝐶⃗ vektörleri ile biçimlenmiş bir paralel prizmanın hacmini hesaplayınız.
4) 𝐴𝐴⃗, 𝐵𝐵
�⃗ = −𝚤𝚤̂𝑥𝑥 + 3. 𝚤𝚤̂𝑦𝑦 + 5. 𝚤𝚤̂𝑧𝑧 ve 𝐶𝐶⃗ = 5. 𝚤𝚤̂𝑥𝑥 − 2. 𝚤𝚤̂𝑦𝑦 − 2. 𝚤𝚤̂𝑧𝑧
𝐴𝐴⃗ = 2. 𝚤𝚤̂𝑥𝑥 + 𝚤𝚤̂𝑦𝑦 − 2. 𝚤𝚤̂𝑧𝑧 , 𝐵𝐵
ÇÖZÜM:
Paralel prizmanın hacminin hesaplanması için skaler üçlü çarpım kullanılır.
2
1 −2
�⃗ × 𝐶𝐶⃗� = �−1 3
Hacim= 𝐴𝐴⃗. �𝐵𝐵
5 � = 57
5 −2 −2
5) Orijinden G(2, -2 ,-1) noktasına doğru olan birim vektör ifadesini yazın.
ÇÖZÜM:
G vektörünün genliği;
𝐺𝐺⃗ = 2. 𝚤𝚤̂𝑥𝑥 − 2. 𝚤𝚤̂𝑦𝑦 − 𝚤𝚤̂𝑧𝑧
|𝐺𝐺| = �(2)2 + (−2)2 + (−1)2 = 3
𝚤𝚤̂𝑔𝑔 =
𝐺𝐺⃗
2
2
1
= 𝚤𝚤̂𝑥𝑥 − . 𝚤𝚤̂𝑦𝑦 − 𝚤𝚤̂𝑧𝑧
|𝐺𝐺| 3
3
3
6) Havadaki, sonsuz uzunluklu, düzgün, yük yoğunluğu 𝜌𝜌ℓ = 20 𝑛𝑛𝑛𝑛/𝑚𝑚 olan doğrusal çizgisel yük z
ekseni boyunca yer almaktadır. (6,8,3) noktasındaki Elektrik alan şiddeti ifadesini bulunuz.
ÇÖZÜM:
𝐸𝐸�⃗ =
𝑟𝑟 = �62 + 82 = 10 𝑚𝑚
𝜌𝜌ℓ
. 𝚤𝚤̂ =
2. 𝜋𝜋. 𝜀𝜀0 . 𝑟𝑟 𝑟𝑟
20 × 10−9
𝑉𝑉
. 𝚤𝚤̂𝑟𝑟 = 36. 𝚤𝚤̂𝑟𝑟 [ ]
−9
10
𝑚𝑚
2. 𝜋𝜋. �
� . 10
36𝜋𝜋
7) (0, 4m, 0) noktasında Q1=0.35 µC yükü, (3m, 0, 0) noktasında ise Q2=-0.55 µC yükü
bulunmaktadır. (0, 0, 5m) noktasındaki elektrik alan şiddetini bulunuz.
ÇÖZÜM:
Yükler ile elektrik alan hesabı yapılacak olan
nokta arasındaki uzaklık vektörleri:
𝑅𝑅�⃗1 = −4. 𝚤𝚤̂𝑦𝑦 + 5. 𝚤𝚤̂𝑧𝑧
𝑅𝑅�⃗2 = −3. 𝚤𝚤̂𝑥𝑥 + 5. 𝚤𝚤̂𝑧𝑧
Uzaklık vektörlerinin genlikleri ve aynı yöndeki
birim vektörler;
�𝑅𝑅�⃗1 � = √16 + 25 = √41
𝚤𝚤̂𝑅𝑅1 =
�𝑅𝑅�⃗2 � = √9 + 25 = √34
𝚤𝚤̂𝑅𝑅2 =
𝐸𝐸�⃗1 =
𝐸𝐸�⃗2 =
−3. 𝚤𝚤̂𝑥𝑥 + 5. 𝚤𝚤̂𝑧𝑧
−4. 𝚤𝚤̂𝑦𝑦 + 5. 𝚤𝚤̂𝑧𝑧
√41
√34
0.35×10−6
−4.𝚤𝚤̂𝑦𝑦 +5.𝚤𝚤̂𝑧𝑧
10−9
4𝜋𝜋(
)(41)
36𝜋𝜋
�
10−9
4𝜋𝜋(
)(34)
36𝜋𝜋
�
−0.55×10−6
√41
� = −48. 𝚤𝚤̂𝑦𝑦 + 60. 𝚤𝚤̂𝑧𝑧
−3.𝚤𝚤̂𝑥𝑥 +5.𝚤𝚤̂𝑧𝑧
�
√34
= 74.9. 𝚤𝚤̂𝑥𝑥 − 124.9. 𝚤𝚤̂𝑧𝑧
[V/m]
[V/m]
𝐸𝐸�⃗ = 𝐸𝐸�⃗1 + 𝐸𝐸�⃗2 = 74.9. 𝚤𝚤̂𝑥𝑥 − −48. 𝚤𝚤̂𝑦𝑦 − 64.9. 𝚤𝚤̂𝑧𝑧 [V/m]
8) Şekilde verilen, eşit fakat zıt yüklü aralarında d kadar mesafe olan iki plaka arasında, plakalardan
d/4 uzaklıkta bulunan A ve B noktalarında oluşacak elektrik alan şiddetleri arasındaki oranı
bulunuz.
ÇÖZÜM: Elektrik alan paralel plakalar arasında sabittir, iki noktadaki elektrik alan eşittir.
1
3𝜋𝜋
9) x=0m ‘de yüzeysel yük dağılımı 𝜌𝜌𝑠𝑠1 = � � 𝑛𝑛𝑛𝑛/𝑚𝑚2 olan sonsuz tabaka, x=4m’de yük dağılımı
−1
3𝜋𝜋
𝜌𝜌𝑠𝑠2 = � � 𝑛𝑛𝑛𝑛/𝑚𝑚2 olan sonsuz tabaka ve x=6m, y=0 koordinatlarında 𝜌𝜌𝑙𝑙 = −2𝑛𝑛𝐶𝐶/𝑚𝑚 olan sonsuz
uzun çizgisel yük dağılımı bulunmaktadır. (2m, 0, 2m) koordinatlarında elektrik alan şiddetini
hesaplayınız.
ÇÖZÜM: Üç yük dağılımı da z’e paraleldir. Dolayısıyla elektrik alan bileşeninin z bileşeni olmayacaktır.
Dolayısıyla (2, 0, 2) noktasındaki alan ile (2, 0, z) noktasındaki alan birbirine eşittir.
𝐸𝐸�⃗ =
𝜌𝜌𝑠𝑠1
𝜌𝜌𝑠𝑠2
𝜌𝜌𝑙𝑙
. 𝚤𝚤̂𝑛𝑛 +
. 𝚤𝚤̂𝑛𝑛 +
𝚤𝚤̂
2𝜀𝜀0
2𝜀𝜀0
2𝜋𝜋𝜋𝜋0 𝑟𝑟 𝑟𝑟
= 6. 𝚤𝚤̂𝑥𝑥 + 6. 𝚤𝚤̂𝑥𝑥 + 9. 𝚤𝚤̂𝑥𝑥
𝑉𝑉
= 21. 𝚤𝚤̂𝑥𝑥 [ ]
𝑚𝑚
10) Şekilde gösterildiği gibi, r ≤ a, z=0’da bulunan düzgün yüzeysel yük yoğunluğuna sahip diskin, (0,
∅, h) koordinatlarında oluşturacağı elektrik alan şiddeti ifadesini bulunuz.
ÇÖZÜM: r bileşenleri birbirini
götürecektir. Sadece z bileşeni kalacak.
𝐸𝐸�⃗ =
=
𝜌𝜌𝑠𝑠 . ℎ 2𝜋𝜋 𝑎𝑎 𝑟𝑟. 𝑑𝑑𝑑𝑑. 𝑑𝑑∅
� �
3 . 𝚤𝚤̂𝑧𝑧
4𝜋𝜋𝜀𝜀0 0 0
(𝑟𝑟 2 + ℎ2 )2
𝜌𝜌𝑠𝑠 . ℎ
−1
1
�
+ � . 𝚤𝚤̂𝑧𝑧
4𝜀𝜀0 √𝑎𝑎2 + ℎ2 ℎ
11) Paralel plakalı kondansatörün plakaları arasında hava varken kapasitansı 2 pF’dır. Plakaların
arasındaki mesafe iki katına çıkartılıp, arasına dielektrik malzeme konduğu zaman kapasitans
değeri 4 pF olmaktadır. Dielektrik malzemenin bağıl dielektrik katsayısını hesaplayınız.
ÇÖZÜM:
𝜀𝜀𝑟𝑟 .
𝜀𝜀0 . 𝑆𝑆
= 2 𝑝𝑝𝑝𝑝
𝑑𝑑
𝜀𝜀0 . 𝑆𝑆
= 4 𝑝𝑝𝑝𝑝
2𝑑𝑑
⇒ 𝜀𝜀𝑟𝑟 = 4
12) 4 yük, x ekseni boyunca aralarında d=3 cm mesafe olacak şekilde dizilmişlerdir. Yüklerin değerleri
q1=+2 µC, q2=-1 µC, q3=+1 µC ve q4=+3 µC olduğuna göre q1 üzerine uygulanan net elektrostatik
kuvvet nedir?
ÇÖZÜM:
13) Üç yük, kenarları d=1 cm olan eşkenar üçgenin köşelerine yerleştirilmiştir. q3=-4 µC, q1= q2=+1 µC,
olduğuna göre, q3 yüküne etkiyen net kuvveti bulunuz.
ÇÖZÜM:
14) Şekilde kesiti verilen içi boş iletken silindirin iç yarıçapı a, dış yarıçapı b’dir. Silindirde kağıdın
dışına doğru akım akmaktadır. Akım yoğunluğu 𝐽𝐽 = 𝑐𝑐. 𝑟𝑟 2 , (r: silindirin ekseninden olan uzaklık),
c=3x106 A/m4 a=1 cm, b=2 cm olduğuna göre toplam akımı bulunuz.
ÇÖZÜM:
15) Küresel koordinat sisteminin merkezinde Q yükü bulunmaktadır. Şekilde gösterildiği gibi 𝛼𝛼 ≤ 𝜃𝜃 ≤
𝛽𝛽 bölgesinden geçen toplam akıyı hesaplayınız. Eğer α=0 ve β=π/2 olsaydı sonuç ne olurdu?
ÇÖZÜM: Tam küre olsaydı, kürenin yüzeyinden geçecek toplam akı Gauss kanunundan;
�⃗ . ����⃗
𝜓𝜓 = ∫𝑠𝑠 𝐷𝐷
𝑑𝑑𝑑𝑑 = 𝑄𝑄 bulunur. Şekilde verilen bölgenin alanı;
2𝜋𝜋
𝛽𝛽
𝐴𝐴 = ∫0 ∫𝛼𝛼 𝑟𝑟 2 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠. 𝑑𝑑𝑑𝑑. 𝑑𝑑𝑑𝑑 = 2𝜋𝜋𝑟𝑟 2 (𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 − 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐) bulunur.
Tanımlı bölgeden geçen net akı;
𝜓𝜓𝑛𝑛𝑛𝑛𝑛𝑛 =
Eğer α=0 ve β=π/2 olsaydı (Yarım küre);
𝐴𝐴
𝑄𝑄
. 𝑄𝑄 = (𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 − 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐)
2
4𝜋𝜋𝑟𝑟
2
𝜓𝜓𝑛𝑛𝑛𝑛𝑛𝑛 =
𝑄𝑄
2
16) Toplam yükü 40/3 nC olan düzgün yüzeysel yük dağılımına sahip dairesel diskin yarıçapı 2m’dir.
Diskin ekseninden 2m ilerisindeki potansiyeli bulunuz.
ÇÖZÜM: Toplam yük verilmiş, öncelikle yüzeysel yük yoğunluğunu bulmamız gerekmektedir:
𝜌𝜌𝑠𝑠 =
𝑄𝑄
𝐴𝐴
=
10−8
3𝜋𝜋
C/m2
𝑅𝑅 = √4 + 𝑟𝑟 2 m
𝑉𝑉 =
30 2𝜋𝜋 2 𝑟𝑟. 𝑑𝑑𝑑𝑑. 𝑑𝑑𝑑𝑑
� �
= 49.7 𝑉𝑉
𝜋𝜋 0 0 √4 + 𝑟𝑟 2
17) Şekilde verilen kondansatörün palakaları arasında bağıl dilektrik katsayısı 𝜀𝜀𝑟𝑟 = 4.5 olan dielektrik
malzeme vardır. Kapasitansını hesaplayınız.
ÇÖZÜM:
Plakalar arasındaki potansiyel farkı bulalım:
𝛼𝛼
𝐷𝐷𝜙𝜙
𝐷𝐷𝜙𝜙 𝛼𝛼
𝐷𝐷𝜙𝜙 . 𝑟𝑟. 𝛼𝛼
𝑉𝑉0 = − � 𝐸𝐸�⃗ . ���⃗
𝑑𝑑𝑑𝑑 = − � �
. 𝚤𝚤̂𝜙𝜙 � . �𝑟𝑟. 𝑑𝑑𝑑𝑑. 𝚤𝚤̂𝜙𝜙 � = −
� 𝑑𝑑𝑑𝑑 = −
𝜀𝜀0 . 𝜀𝜀𝑟𝑟
𝜀𝜀0 . 𝜀𝜀𝑟𝑟
𝜀𝜀0 . 𝜀𝜀𝑟𝑟 0
0
Kapasitansı bulabilmek için plakaların üzerindeki toplam yükü bulmamız lazım. Akı yoğunluğu
vektörünü kullanarak hesaplayabiliriz.
𝐷𝐷𝜙𝜙 = −𝜀𝜀0 . 𝜀𝜀𝑟𝑟 . 𝑉𝑉0 /r.α ve 𝜙𝜙 = 𝛼𝛼’daki plakada yük yoğunluğu;
Plaka üzerindeki toplam yük;
𝜌𝜌𝑠𝑠 = 𝐸𝐸𝑛𝑛 . 𝜀𝜀 = 𝐷𝐷𝑛𝑛 = −𝐷𝐷𝜙𝜙 =
ℎ
𝑟𝑟2
𝑄𝑄 = � 𝜌𝜌𝑠𝑠 𝑑𝑑𝑑𝑑 = � �
0
Kapasitans;
=
𝐶𝐶 =
𝑟𝑟1
𝜀𝜀0 . 𝜀𝜀𝑟𝑟 . 𝑉𝑉0
r. α
𝜀𝜀0 . 𝜀𝜀𝑟𝑟 . 𝑉𝑉0
. 𝑑𝑑𝑑𝑑. 𝑑𝑑𝑑𝑑
r. α
ℎ. 𝜀𝜀0 . 𝜀𝜀𝑟𝑟 . 𝑉𝑉0 𝑟𝑟2
𝑙𝑙𝑙𝑙
α
𝑟𝑟1
𝑄𝑄 ℎ. 𝜀𝜀0 . 𝜀𝜀𝑟𝑟 𝑟𝑟2
=
𝑙𝑙𝑙𝑙
α
𝑟𝑟1
𝑉𝑉0
Sayısal değerler denklemde yerine yazılırsa C= 7.76 pF bulunur.