B Ý R E Y
D E R S H A N E L E R Ý
S I N I F
Ý Ç Ý
D E R S
A N L A T I M
F Ö Y Ü
D E R S H A N E L E R Ý
Konu
F O N K S Ý YO N L A R - I
Bölüm
DAF No.
MF-TM
53
MATEMATÝK - I
53
Bu yayýnýn her hakký saklýdýr. Tüm haklarý bry Birey Eðitim Yayýncýlýk Pazarlama Ltd. Þti.’e aittir. Kýsmen de olsa alýntý yapýlamaz. Metin ve sorular, bu yayýný
yayýmlayan þirketin önceden izni olmaksýzýn elektronik, mekanik, fotokopi ya da herhangi bir kayýt sistemiyle çoðaltýlamaz, yayýmlanamaz.
Örnek 1
FONKSÝYON
A ve B boþ olmayan iki küme olsun. A daki her bir elemaný, B de yalnýz bir elemanla eþleyen baðýntýya A dan B ye
bir fonksiyon denir. Fonksiyonlar genel olarak f, g, ... gibi
küçük harflerle gösterilir.
f
A
A={a, b, c, d}
B={c, d, e, f, g}
kümeleri veriliyor.
Buna göre, aþaðýda verilen A dan B ye tanýmlý baðýntýlardan hangisi fonksiyondur?
B
a
f(A)
1
b
2
A) E1={(a, c), (c, f), (b, e)}
c
3
B) E2={(a, d), (b, e), (c, f), (a, g)}
4
C) E3={(c, a), (d, b), (a, c)}
D) E4={(d, c), (b, f), (c, e), (a, d)}
f
A dan B ye f fonksiyonu f : Ao B veya A oB
E) E5={(a, e), (b, d), (c, b), (d, g)}
þeklinde gösterilir.
f : A o B fonksiyonunda A kümesine f nin taným
kümesi, B kümesine f nin deðer kümesi, A daki elemanlarýn B deki görüntülerinin oluþturduðu kümeye ise
görüntü kümesi denir ve f(A) ile gösterilir.
2
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
o
Örnek 2
1
A dan B ye tanımlanan bir bağıntının fonksiyon
olması için aşağıdaki iki şartın sağlanması
gerekir.
I . f : N o N , f(x)
II. f : Z o N , f(x) 2x 3
• A daki her bir elemanın görüntüsü olmalıdır. Yani,
A da açıkta eleman kalmamalıdır. (B de açıkta
eleman kalabilir.)
• A daki her elemanın yalnız bir tane görüntüsü
olmalıdır. Yani, A daki bir eleman B de birden
fazla elemanla eşleşemez. (Ancak, A daki birkaç
eleman B deki bir elemanla eşleşebilir.)
2
x 4
III. f : R o Z , f(x)
3x – 1
IV . f : R o R , f(x)
x2 – 1
x–3
Yukarýda verilen baðýntýlardan hangileri fonksiyondur?
A dan B ye tanımlanabilecek fonksiyonu sayısı
s(B)s(A) dır.
3
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 3
f : A={ – 3, – 1, 2} o B
f(x)=2x+4
olduðuna göre, f(A) görüntü kümesi aþaðýdakilerden hangisidir?
A) { – 2, 4, 6}
B) { – 8, 0, 2}
D) { – 2, 0, 2}
C) { – 2, 2, 8}
E) {2, 8, 10}
4
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 4
A={x | – 2<x d 4, x tam sayý}
B={y | |y|<3, y doðal sayý}
olduðuna göre, A dan B ye kaç farklý fonksiyon tanýmlanabilir?
5
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 5
f : R o R olmak üzere,
­ x 2 +1 , x t 4
°
f(x) = ®
°̄ x 2 – 1 , x < 4
olduðuna göre, f(5)+f(3) ifadesinin deðeri kaçtýr?
o
z
o
6
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
o
z
Örnek 6
o
f(x)=x2– 3x
a) f(x – 1)=..........................................
o
b) f(3x)=..........................................
7
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 7
Uyarı
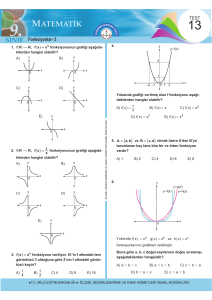
Taným ve deðer kümeleri grafikte verilen y=f(x) biçiminde
tanýmlý aþaðýdaki baðýntýlardan hangisi fonksiyon deðildir?
Grafiği verilen bir bağıntının fonksiyon olup olmadığını
anlamak için, tanım aralığından y eksenine paralel doğrular çizilir. Bu doğrular grafiği yalnız bir noktada kesiyor
ise bağıntı bir fonksiyondur, kesmiyor veya birden fazla
noktada kesiyor ise fonksiyon değildir.
A)
B)
y
y y=x² – 4
y=|– 2x|
O
–4
f:R oR
C)
x
x
O
f:R oR
D)
y y=x3
y
y2=x
O
x
O
x
f:R oR
f:R oR
E)
y
y=x2+3
O
x
f:R oR
8
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
FONKSÝYON TÜRLERÝ
1) ÝÇÝNE FONKSÝYON
f : A oB fonksiyonu için f(A) z B ise, yani B kümesinde en
az bir eleman açýkta kalýyor ise, f ye içine fonksiyon denir.
2) ÖRTEN FONKSÝYON
f : A oB fonksiyonu için f(A)=B ise, f fonksiyonuna örten
fonksiyon denir.
f : A o B fonksiyonunun örten fonksiyon olmasý için, B kümesinde (deðer kümesinde) açýkta eleman kalmamalýdýr.
3) BÝRE BÝR FONKSÝYON
f : A oB fonksiyonu için, A kümesindeki farklý elemanlarýn görüntüleri de farklý elemanlar ise bu fonksiyona
bire bir fonksiyon denir.
9
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
,
Örnek 8
Gerçel sayýlar kümesinde tanýmlý
I. f(x)=2x – 1
II. g(x)=x2+2
III. h(x)=x3
fonksiyonlarýndan hangileri bire birdir?
A) I ve II
B) Yalnýz I
D) I ve III
C) I, II ve III
E) Yalnýz II
(2011/YGS)
10
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
,
Örnek 9
A={1, 2, 3, 4, 5, 6} olmak üzere, f : A o A fonksiyonu bire birdir.
Buna göre,
f(1)+f(2)+f(3)+f(4)
,
toplamýnýn alabileceði en büyük deðer ile en küçük deðer
arasýndaki fark kaçtýr?
A) 6
B) 7
C) 8
D) 9
E) 10
(2013/YGS)
11
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 10
4) SABÝT FONKSÝYON
A kümesindeki tüm elemanlarý B kümesinde yalnýz bir
elemanla eþleyen fonksiyona sabit fonksiyon denir.
f : R oR olmak üzere,
f(x)=(8+4b)x2+(a – 3)x+2a – 5b
Her xA için f(x)=c ve cB ise f, A dan B ye tanýmlý sabit bir fonksiyondur.
fonksiyonu sabit fonksiyon olduðuna göre, f(4) kaçtýr?
R oR
12
R oR
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
R oR
Örnek 11
Uyarı
d
a, b, c ve d sıfırdan farklı gerçek sayılar ve x ≠ –
c
olmak üzere,
ax + b
f(x) =
cx + d
a b
ifadesinin sabit fonksiyon olması için
= olmalıdır.
c d
f : R – { – 4} o R olmak üzere,
f(x)
(a – 3)x 2 bx – 2
x4
sabit fonksiyon olduðuna göre, a+b toplamý kaçtýr?
13
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
5) BÝRÝM (ÖZDEÞ) FONKSÝYON
Örnek 12
f : A o A bir fonksiyon olsun.
f : R o R olmak üzere,
Her xA için f(x)=x ise f fonksiyonuna birim (özdeþ)
fonksiyon denir.
f(x)=(a+2)x2+bx+3x+a+b+c
birim fonksiyon olduðuna göre, a.b.c çarpýmý kaçtýr?
Birim fonksiyon ,(x) = x þeklinde yazýlýr.
Birim fonksiyon bire bir ve örtendir.
14
R oR
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
6) DOÐRUSAL FONKSÝYON
f : R o R ye tanýmlý f(x)=ax+b fonksiyonuna doðrusal
fonksiyon denir.
Örnek 13
f doðrusal fonksiyondur.
f(2)=7
f( – 1)= – 5
olduðuna göre, f(4) kaçtýr?
15
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 14
f doðrusal fonksiyondur.
f(x – 4)+f(2x+1)=6x
olduðuna göre, f(x) fonksiyonu aþaðýdakilerden hangisidir?
A) 2x – 3
B) 3x – 2
D) 2x – 1
C) 2x+3
E) 3x+2
16
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 15
f(x)=f(x+1)+2
f(3)=5
olduðuna göre, f(23) kaçtýr?
17
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 16
R gerçel sayýlar kümesi üzerinde tanýmlý bir f fonksiyonu
x Her x [ – 10, 10] için f(x)=|x|
x Her x R için f(x)=f(x+20)
özelliklerini saðladýðýna göre, f(117) deðeri kaçtýr?
A) 3
B) 4
C) 6
D) 7
E) 9
(2012/YGS)
18
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 17
Aþaðýda A={a1, a2, a3} ve B={b1, b2, b3, b4, b5} kümeleri
verilmiþtir.
f
A
b1
a1
B
b2
a2
b3
a3
b4
b5
A dan B ye f(a2)=b4 olacak biçimde kaç tane birebir f fonksiyonu tanýmlanabilir?
A) 24
B) 20
C) 16
19
D) 12
E) 10
(2008/ÖSS)
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
Örnek 18
I. f(x)=2x
II. f(x)=2 x
III. f(x)=x 2
fonksiyonlarýndan hangileri, her a ve b gerçel sayýsý için
f(a+b)=f(a) . f(b) eþitliðini saðlar?
A) Yalnýz I
B) Yalnýz II
D) I ve III
C) I ve II
E) II ve III
(2013/YGS)
20
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
1.
A={0, 1, 2, 3} kümesinden, B={a, b, c, d} kümesine
tanýmlanan aþaðýdaki baðýntýlardan hangisi bir fonksiyon deðildir?
A) {(0, a), (1, b), (2, c), (3, d)}
B) {(0, a), (1, a), (2, c), (3, c)}
C) {(0, a), (1, c), (2, b), (3, d)}
D) {(0, a), (1, a), (2, a), (3, a)}
E) {(0, a), (0, b), (1, c), (2, d), (3, c)}
21
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
2.
f : { – 2, – 1, 1, 2} o R olmak üzere,
f={( – 1, – 2), ( – 2, 3), (1, 4), (2, 5)}
olduðuna göre, f( – 2)+f(2)+f( – 1) toplamý kaçtýr?
A) 4
B) 5
C) 6
22
D) 7
E) 8
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
3.
f : {1, 2, 3, 4} o R olmak üzere,
x o f(x)=2x – 1
olduðuna göre, f(x) fonksiyonunun görüntü kümesindeki elemanlarýn toplamý kaçtýr?
A) 8
B) 9
C) 10
23
D) 12
E) 16
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
4.
A={a, b, c}
B={a, b, c, d, e}
olduðuna göre, B den A ya kaç farklý fonksiyon tanýmlanabilir?
A) 15
B) 81
C) 125
24
D) 243
E) 625
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
5.
Bir f fonksiyonu, “Her bir pozitif tam sayýyý kendisinin üç
katýnýn 5 fazlasýna götürüyor.” þeklinde tanýmlanmýþtýr.
Bu fonksiyon aþaðýdakilerden hangisi ile gösterilebilir?
A) f(x)=3x – 5
B) f(x)=x+5
D) f(x)=6x – 5
C) f(x)=3x+5
E) f(x)=3x – 10
25
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
6.
f(x)=|x – 2| – |x|
olduðuna göre, f( – 1)+f(0)+f(1) toplamý kaçtýr?
A) – 4
B) – 2
C) 0
D) 2
E) 4
(2003/ÖSS)
26
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
7.
f(x)
­ 3x – 2 ,
° 2
®x – 1 ,
°x 2 ,
¯
olduðuna göre,
A) 3
B) 1
x –3
–3dx3
xt3
f(– 4)+ f(0)
ifadesinin deðeri kaçtýr?
f(3)
C) 0
27
D) – 2
E) – 3
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
8.
f : R o R olmak üzere,
f(x – 3)=2x – 5
olduðuna göre, f( – 5) kaçtýr?
A) – 5
B) – 7
C) – 9
28
D) – 11
E) – 15
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
9.
Aþaðýda grafikleri çizilen E baðýntýlarýndan hangisi R o R
bir fonksiyondur?
y
A)
x
O
C)
y
B)
O
y
y
D)
O
x
O
x
x
y
E)
O
29
x
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
10.
A={a, b, c, d}
kümesi üzerinde tanýmlý aþaðýdaki fonksiyonlarýn hangisi bire birdir?
A) {(a, b), (b, c), (c, d), (d, b)}
B) {(a, c), (b, d), (c, d), (d, a)}
C) {(a, b), (b, c), (c, d), (d, a)}
D) {(a, d), (b, c), (c, a), (d, a)}
E) {(a, b), (b, c), (c, d), (d, d)}
30
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
11.
A={1, 2, 3, 4}
kümesi üzerinde tanýmlý aþaðýdaki fonksiyonlarýn hangisi bire bir ve örtendir?
A) {(1, 2), (2, 1), (3, 2), (4, 3)}
B) {(1, 1), (2, 2), (3, 4), (4, 4)}
C) {(1, 3), (2, 4), (3, 1), (4, 2)}
D) {(1, 2), (2, 3), (3, 4)}
E) {(1, 2), (2, 3), (3, 3), (4, 3)}
31
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
E
R oR
12.
f(x+2)=f(x)+6
f(1)=2
olduðuna göre, f(5) kaçtýr?
A) 7
B) 8
C) 10
32
D) 11
E) 14
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
13. f : R o R olmak üzere,
f(5)=10
f(x – 1)=f(x+3) – 12
olduðuna göre, f(13) kaçtýr?
A) 26
B) 28
C) 30
33
D) 32
E) 34
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
14. f : A oB olmak üzere,
f(x)
2x – 1
3
f(A) {1, 1, 3}
olduðuna göre, A kümesindeki elemanlarýn çarpýmý
kaçtýr?
A) – 10
B) – 5
C) – 2
34
D) 7
E) 10
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(x)=x2+x+1
15.
olduðuna göre, f(a+1) – f(a – 1) ifadesi aþaðýdakilerden hangisine eþittir?
A) 0
B) 2a+1
D) 4a
C) 2a+3
E) 4a+2
35
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(2n)=4 – f(2n – 1)
16.
f(1)=3
olduðuna göre, f(4) kaçtýr?
A) 1
B) 2
C) 3
36
D) 4
E) 5
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(x)=x.f(x – 1)
17.
f(1)=1
olduðuna göre, f(9) kaçtýr?
A) 5!
B) 6!
C) 7!
37
D) 8!
E) 9!
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(x)=2x – 1
18.
olduðuna göre, f(x+2) nin f(x) cinsinden eþiti aþaðýdakilerden hangisidir?
B) [f(x)]2
A) 2.f(x)
D) 4.f(x)
C) 8.f(x)
E)
38
4.[f(x)]2
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
19. f : Z+ o R olmak üzere,
f(x)=3x.(x – 1)!
olduðuna göre,
f(x +1)
ifadesinin eþiti aþaðýdakilerf(x – 1)
den hangisidir?
A) 9x.(x+1)
B) 9x.(x+2)
D) 9x.(x – 2)
C) 9x.(x+1).(x+2)
E) 9x.(x – 1)
39
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(x)=23x – 1
20.
olduðuna göre, f(2x) in f(x) cinsinden ifadesi aþaðýdakilerden hangisidir?
B) 3[f(x)]2
A) 3f(x)
D)
2[f(x)]2
C) 2f(x)
E)
2[f(x)]3
(1990/ÖYS)
40
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
21. f : R o R olmak üzere,
f(x)=2x+1
olduðuna göre, f(3a+b) ifadesi aþaðýdakilerden hangisine eþittir?
A) f(6a+2b) – 1
B) f(3a – b)+1
D) f(3a) – f(b) – 1
41
C) f(3a) – f(b) – 2
E) f(3a)+f(b) – 1
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(x) 22.
2f(x 2) 1
2
f(0) 3
olduðuna göre, f(20) kaçtýr?
A) – 5
B) – 2
C) 0
42
D) 3
E) 10
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
f(x)=2ax – 4x+2a – 1
23.
fonksiyonu sabit bir fonksiyon olduðuna göre, f(10)+f(44)
ifadesinin deðeri kaçtýr?
A) 1
B) 2
C) 3
43
D) 6
E) 9
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
24. f : R o R ve g : R o R
f(x)=x+a+3b
g(x)=(b+1)x+5
fonksiyonlarý veriliyor.
f fonksiyonu birim fonksiyon, g fonksiyonu sabit fonksiyon olduðuna göre, a+b toplamý kaçtýr?
A) 2
B) 3
C) 4
44
D) 6
E) 8
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
25. f : R o R olmak üzere,
f(x)=(a – 2 – x)a+(b+2+x)b
sabit fonksiyon olduðuna göre, f(x) aþaðýdakilerden
hangisine eþittir?
A) 0
B) a2
C) 2a2
45
D) a2– a
E) a2+a
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
26. f(x) birim fonksiyondur.
f(x)=(m – 3)x+2n+m+6
olduðuna göre, m+n toplamý kaçtýr?
A) 4
B) 2
C) 1
46
D) – 1
E) – 2
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
27. f(x) doðrusal fonksiyondur.
f(2)=10
f(5)=19
olduðuna göre, f(3) kaçtýr?
A) 12
B) 13
C) 14
47
D) 15
E) 17
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
28. f(x) doðrusal fonksiyondur.
f( – 2x)+f(x+3)=3x – 5
olduðuna göre, f(1) kaçtýr?
A) 5
B) 3
C) 1
48
D) – 1
E) – 3
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
29. Aþaðýda A={1, 2, 3, 4} ve B={a, b, c, d, e} kümeleri verilmiþtir.
A
a
1
B
b
2
c
3
d
4
e
A dan B ye f(1)=a ve f(2)=c olacak biçimde kaç tane
bire bir f fonksiyonu tanýmlanabilir?
A) 3
B) 4
C) 6
49
D) 8
E) 12
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53
30. Gerçek sayýlar kümesi üzerinde tanýmlý,
I. f(x)=3x+1
II. g(x)=x2+13
III. h(x)=2x3
fonksiyonlarýndan hangileri örtendir?
A) I ve II
B) Yalnýz I
D) I ve III
C) II ve III
E) I, II ve III
50
2013-2014 - DAF - MATEMATÝK - I (MF-TM) - 53