Prof. Dr. Halim Özdemir Yrd. Doç. dr. Nesrin güler

3.5 Varyans Bilinmediğinde Kitle Ortalamasının Aralık Tahmini
Önceki kısımda kitle varyansı,  2 ‘nin bilindiğini kabul ettik ve bu bize,  X   
N
‘nın bir

standart normal yoğunluğa sahip olduğunu söyleme fırsatı verdi. Genelde birçok problemde
 2 bilinmemektedir ve S X2 ile tahmin etmek gerekir. O halde  X   
SX
ortalamanın örneklem standart hatası denir.
, X N ‘ler bilinmeyen  ortalamalı ve  2 varyanslı normal dağılıma
X 
SX
N
al
im
t N 1 
in
Ö
sahip rasgele değişkenler ise,
es
r
Teorem 3.5.1: X1 , X 2 ,
S
X 
alınır. S X  X gösterimine
SX
N
N
r
istatistiği, yani t N 1 
istatistiği yerine
gü
le
N

ir
X  
zd
em
t N 1 adı verilen
N
rasgele değişkeni   N  1 serbestlik dereceli Student- t (ya da T ) dağılımına sahiptir.
N
H
İspat: Gösterilmesi gereken t N 1 rasgele değişkeninin, standart normal dağılıma sahip bir
r.
rasgele değişken ile bundan bağımsız olan ve serbestlik derecesine bölünmüş bir rasgele

2 
  ,
 olduğunu
N 

D
.d
r.
değişkeninin karekökünün bölümü olarak yazılabilmesidir: X
( Xi


X 


  
 N 
 N  1 S X 2
oç


X 


  
 N 

 N  1 S X 2
 2  N  1
X 

SX
N
.D
t N 1 
Yr
d
Pr
o
f.
biliyoruz;
   ,  2  olmak üzere
2
1
1


N  1 S X 2 
2 

 N  1
N
N
i 1
i 1
( X i  X )2  
2 

 2

( X i  X )2
2
değişkeni
 N2 1 ağılımına sahiptir). X ve S X 2 birbirinden bağımsız olduğundan tN 1 , N  1 serbestlik
dereceli Student- t dağılımına sahiptir.
r
gü
le
in
es
r
N
H
al
im
Ö
zd
em
ir
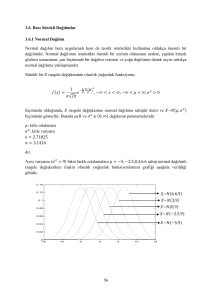
Aşağıdaki şekilde görüldüğü gibi Student- t dağılımının grafiği N  1 ‘in farklı değerleri için
değişir; ancak esas itibariyle biraz genişçe olması hariç, normal dağılım eğrisine benzer.
Sezgisel olarak, N artarken t dağılımı ve normal dağılım arasındaki farkın azalacağı
umulabilir. N  30 için hemen hemen ayırt edilemezler. Student- t dağılımının eğrisi
altındaki alan sayısal olarak hesaplanmıştır. (Normal yoğunluk için olduğu gibi). Bununla
birlikte, N  1 ‘in her değeri için ayrı bir tablo gerekecektir. Bu nedenle alanların tam tablosu
verilemez. Bu nedenle, daha önemli ve ortak olarak kullanılan alanların bazıları tablo şeklinde
verilir.
.d
r.
oç
.D
Yr
d
Pr
o
f.
D
düşer.
r.
Tanım: t , Student- t eğrisi üzerinde öyle bir noktadır ki t ‘nın soluna alanın  kadarı
Örnek: N  1  10 s.d. için t0.05  1.812 ve t0.95  1.812 ‘dir.
Normal dağılım eğrisindeki gibi, Student- t eğrisinin de simetrik oluşu t  t1 olmasını
gerektirir.  2 bilinmediğinde,  için bir güven aralığının oluşumu  tablolarının yerine t
tablolarının
kullanılmasıyla,  2 'nin bilinmesi
halindekine
N  10, N 1  9,   0.05 ise ve %95 ‘lik güven aralığı istiyorsak;
benzer.
Örneğin,




X 
  t0.025  t  t0.975   0.95 ya da   2.26 
 2.26   0.95
SX




N


dir. Yeniden düzenlenirse,

  0.95

ir
S
S

  X   2.26  X    X   2.26  X
N
N

in
al
im
aralığının  ‘yü kapsadığı söylenir.
Ö
SX
S 

, X   2.26  X 
 X   2.26 
N
N

r
0.95 güvenle
gü
le
zd
em
yazılır. O halde X ve S X hesaplanır. Olasılıktan bahsetmenin anlamı yoktur. Bunun yerine
es
r
, X N değişkenleri bilinmeyen  2 varyanslı ve bilinmeyen  ortalamalı bir
Tanım: X1 , X 2 ,
normal yoğunluktan alınan N rasgele değişkenin bir örneklemi ise
r.

  1 

N
H

S
S
 X t   X    X  t   X
1
1
N
N

2
2
.d
r.
Yr
d
.D
olarak tanımlanır.

SX
S 
, X t   X 
 X  t1 
1
N
N

2
2
oç
Pr
o
f.
D
ifadesine dayanarak,  için güven aralığını 1   düzeyinde,
Örnek: 10 hastaya A ve B olarak nitelendirilen iki çeşit uyutucu ilaç verilmiştir. Her bir
hasta için B ilacının etkisinin A ilacından çok olduğu saptanmıştır. Fazla uyku saatlerinin 
ortalaması için %95 ‘lik güven aralığını bulunuz.
Hasta
B ilacı ile
kazanılan
fazla
uyku
saatleri
1
2
3
4
5
6
7
8
9
10
1.2
2.4
1.3
1.3
0.0
1.0
1.8
0.8
4.6
1.6
Çözüm: X  1.58 saat olup
ir
1 10
 ( X i  X )2  1.513  S X  1.23,
9 i 1
zd
em
1
1

 t0.975  2.26 
2
(X t
1

2

 t0.975  t0.025  2.26 ve buradan
2
SX
S
1.23
1.23
, X  t   X )  (1.58  2.26 
,1.58  2.26 
)
1
N
N
10
10
2
Ö
t

r
N  10  N 1  9 s.d., 1    0.95    0.05  t
gü
le
SX 2 
 0.70, 2.46 
es
r
al
im
in
olur. Böylece %95 güvenle  ortalaması 0.70 saat ile 2.46 saat arasında kalacaktır.
N
.d
r.
D
r.
H

 S
NOT: Güven aralığının uzunluğu iki uç noktasının farkıdır, yani L  2  t   X dir.
 1 2  N
Aralığın merkezinin ve uzunluğunun örneklemden örnekleme değiştiğine dikkat edelim.
3.6 Kitle Standart Sapması ve Varyansı İçin Aralık Tahmini
oç
, X N değişkenlerinin  2 varyanslı normal dağılımlı rasgele değişkenler ve
Yr
d
Tanım: X1 ,
.D
Pr
o
f.
 2 ve  ‘yı tahmin etmek istiyorsak, çalışmamıza  2 ‘nin minimum varyanslı yansız tahmin
edici ile devam etmek uygun olur.
SX 2 
1 N
( X i  X )2

N  1 i 1
olmak üzere

2
N 1
N  1 S X 2


2
istatistiğine   N  1 serbestlik dereceli ki-kare istatistiği denir.
r
gü
le
in
es
r
al
im
Ö
zd
em
ir
2
NOT: t yoğunluğu gibi,  yoğunluğu da N  1'in farklı değerleri için (örneğin, şekideki
gibi) değişir.  2 negatif olmadığından yoğunluk, solda "0" ile sınırlı fakat sağda sınırsızdır.
N
H
 2 olasılık yoğunluk fonksiyonu eğrisi altındaki alanlar sayısal olarak hesaplanmıştır. Bunun
içinde çok kullanılan alanların listesi verilmektedir.
oç
.D
Yr
d
Pr
o
f.
D
kadarı düşer.
.d
r.
r.
Tanım:  2 noktası,  2 yoğunluğu üzerinde öyle bir noktadır ki onun soluna alanın 
Örnek: N  1  10 s.d. için  20.05  3.94 ve  20.95  18.31' dir. dir.
Açıkça görüldüğü gibi  2 eğrisi simetrik değildir ve  2   21 ' dır. %95 ‘lik bir güven
aralığı hesaplamak için,
   20.025   2 N 1   20.975   0.95
yazılır. Örneğin, N  10  N 1  9 ise
Ö
  N  1 S X 2
N  1 S X 2 

2

 
  0.95
2.70 
 19.00
r
dır. Buradan yapılacak düzenlemelerle,
gü
le
zd
em
ir

 N  1 S X 2  19.00  0.95
  2.70 

2


yazılır. Örneklemden S X 2 ‘nin değeri hesaplandıktan sonra  2 için %95 ‘lik bir güven
in
es
r
al
im
aralığından bahsedilebilir.
H
rasgele değişkenin bir grubu X1 ,
oç
.d
r.
f.
D
r.


2
N  1 S X 2 

  N  1 S X
2

 
  1
2 
 2


1
2
2
ifadesine dayanarak,
Pr
o
, X N ise,
N
Tanım: Bilinmeyen  2 varyanslı ve bilinmeyen  ortalamalı bir normal kitleden alınan N
.D


2
2
  N  1 S X  N  1 S X 
,
 2

 2



1

2
2

Yr
d
şeklinde tanımlanan aralığa  2 için 1   güven düzeyli güven aralığı denir.
NOT:  2
1

ve  2 2 teki gibi ya da aralarında 1   oranına sahip herhangi çifti
3
kullanabiliriz. 
3
2
1

2
ve  2  ‘nin kullanıldığı aralığa “Eşit Uzantılı” güven aralığı denir.
2
gü
le
r
ir
zd
em
Ö
Benzer şekilde, yukarıdaki ifadelerde her birinin karekökü alınarak,  için 1   güven
düzeyli güven aralığı,
 2
1
2
2



N
es
r

al
im
2
H
olarak bulunur.

 N  1 S X 2 ,  N  1 S X 2 
in





.d
r.
D
r.
Örnek: Aşağıdaki değerler bir firma tarafından piyasaya sürülen küçük reçel kutularının gram
olarak ağırlıklarıdır : 164, 161, 158, 170, 161, 159, 158, 169, 152, 160. Firma tarafından
28.6, N  1  9;  20.025   2   2.70 ve  20.975   2   19.00
2
2
.D
Pr
o
Çözüm: S X 2
oç
f.
dağıtılan bu tipteki kutuların varyansı için %95 ‘lik güven aralığını bulunuz.
Yr
d


2
2
  N  1 S X  N  1 S X   9   28.6  9   28.6  

,
2
   19 , 2.70   13.5,95.3
 2

  1 
 

2
2

olur.
UYARI: Varyans için bulunan güven aralıkları, orijinal yoğunluğun normallikten ayrılışına
oldukça duyarlıdırlar. Deneyi yapan, kitlenin normal dağılıma sahip olmadığına inanırsa,  2
için yukarıdaki gibi güven aralığı hesaplarken dikkatli olmalıdır.
3.7 İki Normal Ortalamanın Farkının Aralık Tahmini
Sırasıyla, bilinmeyen 1 ve  2 ortalamalı 1 ve 2 nolu iki normal kitleden N ve M
hacimlik örneklemler seçtiğimizi varsayalım. Sırasıyla, X 1 ve X 2 onların örneklem
ortalamalarıysa, 1  2 ‘nin nokta tahmin edicisinin X1  X 2 olduğu açıktır. Önce  12 ve  22
kitle varyanslarının bilindiği halini ele alacağız. Teo.3.2.5‘den, X1  X 2 'de normal dağılıma
 X 2    1  2 
 12
N
birim normal dağılıma sahiptir. Bu nedenle

 22
M
veya
es
r
al
im
in
Ö




X 1  X 2    1  2 


   
     1 
1 
 1 2
 12  22
2



N M


r
1
dir. Böylece,
M
ir
X

gü
le

N
 22
zd
em
sahip ve ortalaması 1  2 ve varyansı
 12
N
.d
r.
r.
H

 12  22
 12  22  
   X 1  X 2    

 1  2   X1  X 2    

  1  
1
1
N M
N M  

2
2

oç
f.
D
ifadesi, 1  2 için 1   güven düzeyli bir güven aralığı tanımlar.
1493
1519
Yr
d
A Bölgesi
.D
Pr
o
Örnek: Bir şirket tarafından kullanılan demir A ve B ile nitelendirilen iki bölgeden
çıkartılmaktadır. Demirin erime noktasını öğrenmek amacıyla bu bölgelerden alınan
örneklerin erime noktaları aşağıdaki gibi bulunmuştur.
B Bölgesi
1509
1494
1518
1512
1512
1514
1512
1483
1507
1491
1489
1508
1508
1494
A ve B bölgelerinde erime noktalarının farkı için her iki halde de  2 varyansını  2  100 
biliniyor kabul ederek %95 ‘lik ve %99 ‘lık güven aralıklarını bulunuz.
Çözüm: X A  1506.7, X B  1499.3  X A  X B  7.4;  A2   B2  100

 A2
10

 B2
 A2  B2
 1 1
 100     26.27 

6
10 6
 10 6 
5.16
olur. %95 lik güven aralığı için:
1


1
2
0.01
2
al
im
olur.
 0.995  2.58   5.91; 20.71
Ö

gü
le
%99 ‘lık güven aralığı için : benzer şekilde,
r
ir
2
in

es
r
1

 A2  B2
 A2  B2 
 0.975  1.96   X A  X B    

; X A  X B    

   2.71;17.51 ,
1
1
10
6
10
6

2
2

zd
em

 12 ve  22 bilinmiyor fakat eşit olarak kabul edilirse ve sırasıyla S12 ve S 22 tahmin
N
S p2 
( N  1) S12  ( M  1) S22
N M 2
oç
f.
D
Tanımdan, S p2 tahmin edicisi
.d
r.
r.
H
edicilerine sahipseler:
.D
Z
( X 1  X 2 )  ( 1   2 )

Yr
d
Pr
o
dir. Bu durumda , 12   22   olduğu dikkate alınırsa,
1 1

N M
olur. Şimdi  yerine S p koyarsak, Kısım 3.5 ‘den biliyoruz ki N  N  2 serbestlik dereceli
bir Student -t – istatistiği elde edilir. O halde ,
t
( X 1  X 2 )  ( 1  2 )
1 1
Sp

N M
ve


( X  X 2 )  ( 1  2 )
P  t   1
t 
1
1 1
 1 2
2
S

p

N M


  1


yada

1 1
1 1 
P  X1  X 2  t  S p

 1  2  X 1  X 2  t  S p
   1 
1
1
N M
N M
2
2



ir

zd
em

gü
le
r
bulunur. Bu da 1  2 için 1−α güven düzeyli bir güven aralığı tanımlar.
Ö
Örnek: Bir sınav döneminde istatistik dersinin sınavına giren öğrencilerin 12 ‘si kız , 10 ’u
erkek öğrencidir. Kız öğrencilerin not ortalaması
85, standart sapması
4 ve
erkek
in
al
im
öğrencilerin not ortalaması 81 , standart sapması 5 ’tir. 1 ve  2 sırasıyla bu sınava girmesi
X1  85, X 2  81, N  12, M  10,
( kitle varyansları eşit ve  2 kabul edildi.)
N
H
Çözüm:
es
r
gereken tüm kız ve erkek öğrencilerin not ortalamaları ise , 1  2 farkı için % 90 ‘lık güven
aralığını bulunuz.
r.
X1  X 2  85  4  4 ; 2 ‘nin birleşik tahmini S p2 ,
X
1

.d
r.
1
 t0,95  1, 7247 olduğundan,
2

 X2  t
1

Sp
2


1 1
1 1

 1  2  X 1  X 2  t  S p

1

N M
N M
2
.D
Pr
o
f.
olur.   0,10  t
( N  1) S12  ( M  1) S22 11.16  9.25

 20, 05  S P  4, 478
N M 2
12  10  2
oç
D
S p2 
Yr
d
ifadesinden, gerekli hesaplamalar yapılırsa, 0,69  1  2  7,31 bulunur.