Ödev 1

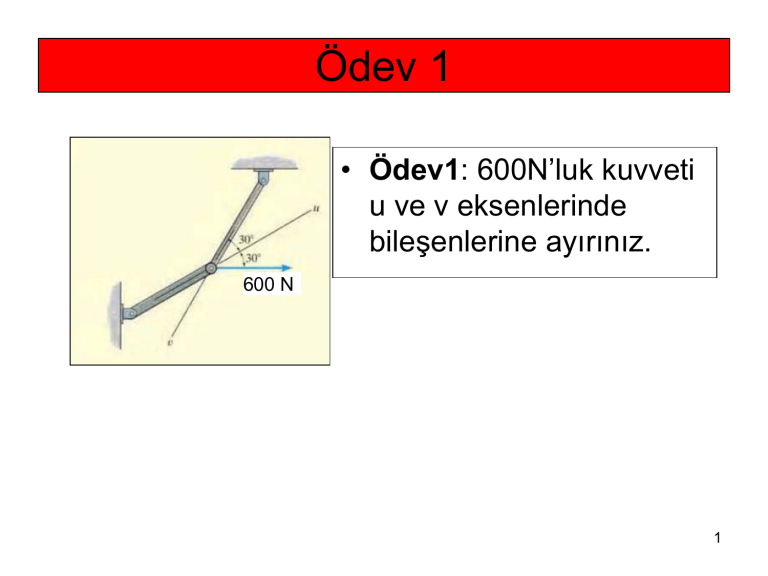
Ödev 1
• Ödev1: 600N’luk kuvveti
u ve v eksenlerinde
bileşenlerine ayırınız.
600 N
1
600 N
Fu
600 N
=
sin 120° sin 30°
Fv
600 N
=
sin 30° sin 30°
600 N
600 N
Fu = 1039 N
Fv = 600 N
2
Ödev 2
• Ödev2: F2 kuvvetinin
şiddetini, yönünü ve bileşke
kuvveti bulunuz. (bileşke
kuvvet x ekseni üzerinde, F2
kuvveti ise minimum şiddette
olsun)
3
• Ödev2: F2 kuvvetinin
şiddetini, yönünü ve bileşke
kuvveti bulunuz. (bileşke
kuvvet x ekseni üzerinde, F2
kuvveti ise minimum şiddette
olsun)
4
Ödev 3
• Ödev3: Etkiyen
kuvvetlerin
bileşkesinin y ekseni
boyunca olması ve
şiddetinin de 800 N
olması için F1
kuvvetinin şiddetini,
θ açısının ne olması
gerektiğini bulunuz
5

  
FR = F1 + F2 + F3
FRy = 800 N
FRx = 0
6
4
=
−
×
+ F1 × sin θ + 400 × cos 30 = 0
F
600
∑ Rx
5
− 480 + F1 × sin θ + 346.41 = 0
F1 × sin θ = 133.59 N
133.59
F1 =
sin θ
3
∑ FRy = 600 × 5 + F1 × cosθ + 400 × sin 30 = 800
240
F1 × cos θ = 240 N
F1 =
cos θ
133.59 240
=
sin θ
cos θ
133.59
= tan θ
240
θ = 29.1
133.59
F1 =
= 275 N
sin 29.1
7
Ödev 4
• ÖDEV4: Şekilde
gösterilen kuvvetlerin
bileşkesini birim
vektörleri kullanarak
bulunuz
8
• ÖDEV4: Şekilde
gösterilen kuvvetlerin
bileşkesini birim
vektörleri kullanarak
bulunuz
ÇÖZÜM 1:
9
10
ÇÖZÜM 2:
11
Ödev 5
• ÖDEV5: F kuvvetini kartezyen
vektör olarak ifade ediniz ve F
kuvvetinin yön kosinüslerini
bulunuz
  
F = F '+ Fz
  
F ' = Fx + Fy
12
13
Ödev 6
• ÖDEV 6: A noktasına etki
eden kuvveti kartezyen
vektör olarak ifade edin.
14
15
Ödev 7
W
• Şekilde gösterilen
kablolarda 0.5 kN’un
üzerinde çekme
kuvveti oluşmaması
için asılı olan kovanın
ağırlığını (W)
bulunuz.
16
E noktasının SCD’ı
3

→ ∑ Fx = 0 FED . cos 30 − FEB ( ) = 0
5
FED = 0.693FEB
+
4
↑ ∑ Fy = 0 FED . sin 30 + FEB ( ) − W = 0
5
0.8 FEB + 0.5(0.693FEB ) = W
FEB = 0.872W
1
17
B noktasının SCD’ı
3

→ ∑ Fx = 0 FBC . cos 30 + FBE ( ) − FBA = 0
5
4
↑ ∑ Fy = 0 FBC . sin 30 − FBE ( ) = 0
5
0.5 FBC = 0.8 FBE = 0.8 × 0.872W
+
2
FBC = 1.395W
1.395W (cos 30) + 0.6(0.872W ) = FBA
FBA = FAB = 1.731W
3
En riskli durum [3]
0.5 = 1.731W
W = 0.289kN
18
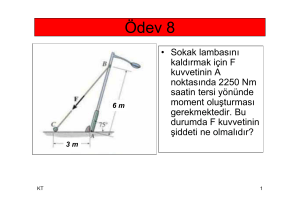
Ödev 8
6m
• Sokak lambasını
kaldırmak için F
kuvvetinin A
noktasında 2250 Nm
saatin tersi yönünde
moment oluşturması
gerekmektedir. Bu
durumda F kuvvetinin
şiddeti ne olmalıdır?
3m
19
20
21
Ödev 9
• F kuvvetinin OA borusunun
doğrultusundan geçen
eksene göre oluşan
momentin şiddetini bulunuz.
22
HATIRLATMA
Pozisyon (Konum) Vektörleri
• Pozisyon vektörü uzaydaki herhangi iki nokta arasında
yönelen bir kartezyen kuvvet vektörünü formüle etmek
açısından önemlidir.
• r pozisyon vektörü, bir noktanın uzaydaki konumunu
diğer bir noktaya göre belirleyen sabit bir vektördür.
23
• Daha genel bir halde, pozisyon vektörü uzaydaki
A noktasından B noktasına da yönelebilir.
Vektör toplamı
24
Bir doğru boyunca yönelen kuvvet vektörü
• Üç boyutlu statik
problemlerinde, bir
kuvvetin doğrultusu
genellikle etki
çizgisinin geçtiği iki
nokta ile belirlenir.
Şekildeki F kuvveti
buna bir örnektir.
Doğrultusu A’dan B’ye
olan F kuvveti
kartezyen vektör
şeklinde ifade
edilebilir.
25
  
M a = ua (r × F )
Bu çarpıma skaler üçlü çarpım denir.
Vektörler kartezyen formda ifade edilirse;
Skaler üçlü çarpım determinant formda da yazılabilir:
26
1. Satır
2. Satır
3. Satır
1.satır: a-a' ekseninin yönünü belirleyen birim vektörün kartezyen bileşenleri
2.satır: a-a ekseninin herhangi bir yerinden, F kuvvetinin etki çizgisinin
herhangi bir yerine olan pozisyon vektörünün kartezyen bileşenleri
3. satır: F kuvvetinin kartezyen bileşenleri
Ma belirlendiğinde Ma’yı kartezyen vektör şeklinde ifade edebiliriz :
Ma negatif çıkarsa


M a = M aua
 
M a u a ‘nın tersi yönündedir.
27
28
29
Ödev 10
Boruya etkiyen kuvvet çiftinin
momentini belirleyiniz.
30
HATIRLATMA
Kuvvet Çiftleri
• Kuvvet çifti, aralarındaki dik uzaklık d olan,
aynı büyüklükte ve zıt yöndeki paralel iki
kuvvet olarak tanımlanır.
• Bileşke kuvvet sıfır olduğundan, kuvvet
çiftinin tek etkisi dönme eğilimi yaratmaktır.
Kuvvet çifti ile üretilen moment, bir
O noktasında oluşan iki kuvvetin
momentleri toplamına eşittir.
   


 
M = rB × F + rA × (− F ) = (rB − rA ) × F
     
rB = rA + r r = rB − rA
  
M = r×F
Momentin, rA, rB konum vektörlerine
değil, sadece kuvvetler arasındaki
konum vektörüne bağlı olması
nedeniyle, kuvvet çiftinin momentinin
bir serbest vektör olduğu, herhangi 31
bir
noktada etki edebileceği söylenebilir.
Skaler Formülasyon
Kuvvet çiftinin momenti:
M = Fd
F= kuvvetlerden birinin büyüklüğü
d= kuvvetler arasındaki dik uzaklık (moment kolu)
Kuvvet çifti momentinin doğrultu ve yönü sağ el
kuralı ile belirlenir.
Vektörel Formülasyon
Kuvvet çiftinin momenti vektörel
(çapraz) çarpımla:
  
M = r ×F
32
• r konum vektörü, i, j, k bileşenleri, vektörün
başlangıcının koordinatları A (xA, yA, zA), ucuna
karşı gelen koordinatlardan B (xB, yB, zB)
çıkartılarak bulunabilir.
• Ayrıca, bu üç
bileşenin
uç
uca eklenmesi
r’yi verir. A’dan
başlıyarak B’ye
ulaşılıyor.
33
25 N
25 N
25 N
25 N
34
35
Ödev 11
Şekilde gösterilen döşeme
birbirine paralel dört kuvvetin
etkisi altındadır. Eşdeğer tekil
kuvvetin yönünü ve yerini
bulunuz.
36
37
38
Ödev 12
Mesnet tepkilerini ve C
noktasında oluşan kuvveti
bulunuz.
39
40
Ödev 13
Şekildeki köprü kafes
sisteminin CF
çubuğundaki kuvveti
belirleyiniz. Çekme veya
basınç kuvveti olduğunu
belirtiniz.
KT
41
ΣM A = 0
− 5kN × 8m − 3kN ×12m + E y ×16m = 0
16 E y = 76 ⇒ E y = 4.75kN
KT
42
6
4
=
4+ x 8+ x
x = 4m
+ ΣMo = 0
− FCF sin 45o (12m) + (3kN )(8m) − (4.75kN )(4m) = 0
FCF = 0.589kN
KT
( BASINÇ )
43
Ödev 14
EF, BC ve CF
elemanlarında oluşan
kuvvetleri ve türünü
bulunuz.
6m
6m
300 N
6m
300 N
9m × tan 30
tan φ =
= 1.732 ⇒ φ = 60o
3m
6m
KT
6m
300 N
6m
300 N
44
KT
45
6m
6m
300 N
KT
6m
300 N
46
Ödev 15
3m
2m
Şekildeki sistemin her
elemanında oluşan
kuvvetleri belirleyiniz.
Çekme veya basınç
kuvveti olduğunu
belirtiniz.
2m
300 N
KT
47
KT
48
Ödev 16
4m
4m
450 N
4m
KT
Şekildeki sistemin her
elemanında oluşan
kuvvetleri belirleyiniz.
Çekme veya basınç
kuvveti olduğunu
belirtiniz.
49
KT
50
KT
51