Elektrik Müh. Temelleri
ELK-184
4
@ysevim61
https://www.facebook.com/groups/KTUEMT/
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
1
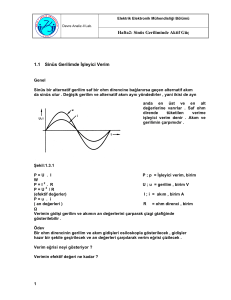
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri
Amacı :
• Devreyi basitleştirerek çözümü kolaylaştırmak.
• İlgilenilen eleman yerine farklı eleman takıldığı zaman bu elemandan geçen
akımı kolay bulmak.
R1
E
+
ıa
R5
R2
R
R3
I
R4
A
A
I
Rth
I
R
+
Vth -
B
Thevenin eşdeğeri
+
IN
Rth
R
-
Norton eşdeğeri
B
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
2
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri
Bu yöntemler birden çok elemana da uygulanabilir. Yöntemi uygularken eşdeğer
devrede ilgilenilen elemanları orijinal devredeki gibi bağlamak gerekiyor.
R1
E
+
ıa
R2
I
R5
R
R4
R3
A
A
I
I
Rth
+
+
Vth -
R5
R
IN
Rth
R
R5
B
Tevenin eşdeğeri
Norton eşdeğeri
B
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
3
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri
1- Rth eşdeğer direncini bulmak için devrede ne kadar kaynak varsa devre dışı
bırakılır.
Akım kaynaklarını devreden çıkarmanın yolu yerini açık devre yapmaktır.
Gerilim Kaynaklarını devreden çıkarmanın yolu yerini kısa devre yapmaktır.
Çıkarılan eleman veya elemanlar tarafından bakılınca görülen eşdeğer direnç
olan Tevenen ve Norton eşdeğer direnci Rth hesaplanır. Bu direnç değeri her
iki yöntemde de aynıdır.
A
R1
I
Rth
E
R
+
Vth -
+
ıa
R5
R2
R
R3
I
R4
A
B
Thevenin eşdeğeri
I
+
IN
Rth
R1
R
R5
R2
Rth
R3
R4
B
Norton eşdeğeri
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
4
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri
2- Thevenen yönteminde Thevenin açık devre gerilimini Vth bulmak için ilgilenilen eleman
devreden çıkarılır ve yeri boş bırakılarak Vth gerilim ataması yapılır. Bu gerilim devre
çözülerek bulunur ve Thevenin eşdeğer devresindeki gerilim kaynağının değeri bu açık
devre gerilimi olarak atanır.
A
I
Rth
R1
R
+
E
Vth -
+
ıa
R5
R2
+
Vth
R3
-
R4
B
Thevenin eşdeğeri
3- Norton yönteminde ilgilenilen eleman devreden çıkarılır ve yeri kısa devre yapılır. Bu
kısa devre yapılan koldan geçen IN akımı devre çözülerek bulunur ve Norton eşdeğer
devresindeki akım kaynağının değeri bulunan bu akım olarak atanır.
A
I
+
IN
Rth
R1
R
E
-
+
ıa
R5
R2
IN
R3
R4
B
Norton eşdeğeri
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
5
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri
4- Thevenen ve Norton yöntemi ile bulunan Eşdeğer dirençler Rth=RN birbirine eşittir. Bu
direnç değeri ve her iki yöntemde bulunan açık devre gerilimi Vth ve kısa devre akımı IN
kullanılarak Thevenen ve Norton eşdeğer devreleri aşağıdaki gibi oluşturularak eleman veya
elemanların istenen akım I ve gerilim değerleri basitleştirilmiş bu eşdeğer devreler üzerinden
hesaplanır.
A
A
I
Rth
I
R
+
Vth -
B
Thevenin eşdeğeri
+
IN
Rth
R
B
Norton eşdeğeri
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
6
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri
NOT: Bir devrede bağımlı akım veya gerilim kaynağı var ise devrenin eşdeğer
direnci Rth bu yöntem ile bulunamaz. Devrenin eşdeğer direnci Tevenen açık
devre gerilimi Vth ve Norton kısa devre akımı IN bulunarak elde edilir.
60Ω
50Ω
Ix
40Ω
E1=100V
200Ω
+
-
RL
+
Ix
50Ω
60.Ix
60Ω
40Ω
E1=100V
Vth
+
200Ω
+
-
+
-
Ix
50Ω
60.Ix
𝑹𝒕𝒉 =
60Ω
𝑽𝒕𝒉
𝑰𝑵
40Ω
E1=100V
+
-
200Ω
+
IN
60.Ix
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
7
Tevenin (Gerilim) ve Norton (Akım) Eşdeğeri
A
A
I
I
R
Devre
≡
Rth
R
+
Vth -
B
𝑰=
𝑽𝒕𝒉
𝑹 + 𝑹𝒕𝒉
B
Tevenin eşdeğeri
Vth, ilgili devrenin açık devre gerilimi.
Rth, ilgili devrenin eşdeğer direnci.
Açık devrede akım sıfırdır, kısa devrede gerilim sıfırdır.
Bütün bağımsız kaynaklar devre dışı bırakılacak.
Bağımsız gerilim kaynağı varsa kısa devre, bağımsız akım kaynağı varsa açık
devre olarak alınacaktır.
A
I
+
IN
Rth
R
-
IN, kısa devre akımı
𝑰𝑵 . 𝑹//𝑹𝒕𝒉
𝑰=
𝑹
Açık devre gerilimi
𝑽𝒕𝒉
=
𝑹𝒕𝒉 =
𝑰𝑵
Kısa devre akımı
B
Norton eşdeğeri
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
8
Thevenin (Gerilim) ve Norton (Akım) Eşdeğeri Farkları
R1
E
+
ıa
I
R5
R2
R
R3
R4
Thevenen veya Norton yöntemi arasındaki tek fark eşdeğeri bulunacak olan eleman
veya elemanlar devreden çıkarılırken Thevenin Yöntemi ise çıkarılan elemanın yeri
açık devre, Norton yöntemi ise kısa devre yapılır ve Thevenen yönteminde açık
devre gerilimi Norton yönteminde kısa devre akımı bulunur.
R1
E
+
ıa
R1
R5
R2
E
R3
R5
R2
R3
R4
Tevenen Yöntemi
Norton eşdeğeri
+
ıa
R4
Norton Yöntemi
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
9
Örnek
I1
R1=3kΩ
I
+
E=48V -
Örnek: R direncinden geçen akımı tevenin eşdeğerini
kullanarak bulunuz.
−𝑬 + 𝑹𝟏 . 𝑰𝟏 + 𝑹𝟐 . 𝑰𝟐 = 𝟎
R=1,25kΩ
R2=1kΩ
𝑹. 𝑰 − 𝑹𝟐 . 𝑰𝟐 = 𝟎
I2
I1
B
𝑰𝟏 = 𝑰𝟐 + 𝑰
I1, I2 ve I bu denklemleri kullanarak çözülür.
B
R1=3kΩ
A
𝑹𝒕𝒉 = 𝑹𝟐 / /𝑹𝟏 =
𝟑.𝟏
= 0,75kΩ
𝟑+𝟏
R2=1kΩ
I2
B
B
I1
R1=3kΩ
E=48V
+
-
A
R2=1kΩ
I2
Vth
B
Tevenin eşdeğeri
𝑽𝒕𝒉 =
𝑬
𝟒𝟖
. 𝑹𝟐 =
.1= 12V
𝑹𝟐 +𝑹𝟏
𝟑+𝟏
Açık devre gerilimi
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
10
Örnek
I1
R1=3kΩ
I
A
E=48V +
-
R=1,25kΩ
R2=1kΩ
I2
B
I1
Kısa devre akımı
R1=3kΩ
E=48V+
-
A
R2=1kΩ
I2
𝑰𝑵 =
𝑬
𝑹𝟏
=
𝟒𝟖
= 16mA
𝟑𝒌
IN
B
Tevenin eşdeğeri
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
11
Örnek
A I
Rth=750Ω
𝑰=
R=1,25kΩ
+
Vth=12V -
𝑽𝒕𝒉
𝟏𝟐
=
= 𝟔𝒎𝑨
𝑹𝒕𝒉 + 𝑹 𝟎, 𝟕𝟓 + 𝟏, 𝟐𝟓
B
Norton eşdeğeri
A
𝑰𝑵 . 𝑹//𝑹𝒕𝒉
𝑰=
𝑹
I
+
IN
Rth
R
-
𝟏𝟔𝒎.
𝑰=
𝟏, 𝟐𝟓 ∗ 𝟎, 𝟕𝟓
𝟏, 𝟐𝟓 + 𝟎, 𝟕𝟓
= 𝟔𝒎𝑨
𝟏, 𝟐𝟓
B
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
12
Örnek
E1=10V
+ R1=5Ω
R2=10Ω
+
E2=5V -
R3=20Ω
I=1A
Ry=6Ω
a) Ry direncine göre devrenin Tevenen eşdeğerini bulunuz ve Ry direncinde
harcanan gücü bulunuz.
b) Ry direncine göre devrenin Norton eşdeğerini bulunuz ve Ry direncinde
harcanan gücü bulunuz.
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
13
Çözüm
R1=5Ω
𝑹𝒕𝒉 = 𝑹𝟐 +
R3=20Ω
R2=10Ω
Rth
E1=10V R1=5Ω
+ -
𝑰𝟐 = 𝑰𝟏 − 𝟏
+
E2=5V -
𝟓. 𝑰𝟏 − 𝟏 − 𝟏𝟎 + 𝑰𝟏 . 𝟐𝟎 = 𝟎
R3=20Ω
1A
𝟓. 𝟐𝟎
= 𝟏𝟎 +
= 𝟏𝟒Ω
𝟓 + 𝟐𝟎
𝑹𝟏 . 𝑰𝟏 − 𝟏 − 𝟏𝟎 + 𝑰𝟏 . 𝑹𝟑 = 𝟎
𝑰𝟏
R2=10Ω
𝑹𝒕𝒉
𝑹𝟏 . 𝑹𝟑
𝑹𝟏 + 𝑹𝟑
I=1A
+
Vth
-
𝟐𝟓. 𝑰𝟏 − 𝟏𝟓 = 𝟎
𝑰𝟏 = 𝟎, 𝟔𝑨
−𝑹𝟑 . 𝑰𝟏 − 𝑹𝟐 . 𝟏 + 𝑬𝟐 − 𝑽𝒕𝒉 = 𝟎
𝑽𝒕𝒉 = −𝟐𝟎. 𝟎, 𝟔 − 𝟏𝟎. 𝟏 + 𝟓
𝑽𝒕𝒉 = −𝟏𝟕𝑽
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
14
Çözüm
A
−𝑹𝒚 . 𝑰𝒚 − 𝑹𝒕𝒉 . 𝑰𝒚 + 𝑽𝒕𝒉 = 𝟎
Iy
𝑹𝒕𝒉 = 𝟏𝟒𝛀
Ry=6Ω
+
𝑽𝒕𝒉 = −𝟏𝟕𝑽-
B
−𝟔. 𝑰𝒚 − 𝟏𝟒. 𝑰𝒚 − 𝟏𝟕 = 𝟎
𝑰𝒚 =
−𝟏𝟕
= −𝟎, 𝟖𝟓𝑨
𝟐𝟎
𝑷𝒚 = 𝑰𝒚 𝟐 . 𝑹𝒚 = 𝟎, 𝟖𝟓
𝟐. 𝟔
𝑷𝒚 = 𝟒, 𝟑𝟑𝟓𝒘
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
15
Çözüm
𝑹𝟏 . 𝑰𝟏 − 𝟏 − 𝑰𝑵 − 𝟏𝟎 + 𝑰𝟏 . 𝑹𝟑 = 𝟎
E1=10V R1=5Ω
𝑰𝟐 = 𝑰𝟏 − 𝟏 − 𝑰𝑵 + -
𝟓. 𝑰𝟏 − 𝟏 − 𝑰𝑵 − 𝟏𝟎 + 𝑰𝟏 . 𝟐𝟎 = 𝟎
𝑰𝟏
R2=10Ω
𝟏 + 𝑰𝑵
+
E2=5V -
𝟐𝟓. 𝑰𝟏 − 𝟓. 𝑰𝑵 = 𝟏𝟓
−𝑹𝟑 . 𝑰𝟏 − 𝑹𝟐 . 𝟏 + 𝑰𝑵 + 𝑬𝟐 = 𝟎
R3=20Ω
I=1A
IN
−𝟐𝟎. 𝑰𝟏 − 𝟏𝟎. 𝟏 + 𝑰𝑵 + 𝟓 = 𝟎
−𝟐𝟎. 𝑰𝟏 − 𝟏𝟎. 𝑰𝑵 = 𝟓
𝟓. 𝑰𝟏 − 𝑰𝑵 = 𝟑
−𝟐. 𝑰𝟏 − 𝑰𝑵 = 𝟎, 𝟓
𝑰𝟏 = 𝟎, 𝟑𝟓𝟕𝑨
𝑰𝑵 = −𝟏, 𝟐𝟏𝟒𝑨
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
16
Çözüm
Norton eşdeğeri
A
𝑰𝒚
𝑰𝑵 = 𝟏. 𝟐𝟏𝟒𝑨
𝑹𝒕𝒉 = 𝟏𝟒𝛀
B
Ry=6Ω
𝑰𝒚 =
𝑹𝒚 . 𝑹𝒕𝒉
𝑰𝑵 . 𝑹 + 𝑹
𝒚
𝒕𝒉
𝑹𝒚
𝟔. 𝟏𝟒
𝟏, 𝟐𝟏𝟒. 𝟔 + 𝟏𝟒
𝑰𝒚 =
𝟔
𝟏, 𝟐𝟏𝟒. 𝟒, 𝟐
𝑰𝒚 =
= 𝟎, 𝟖𝟒𝟗𝑨
𝟔
𝑷𝒚 = 𝑰𝒚 𝟐 . 𝑹𝒚 = 𝟎, 𝟖𝟓
𝟐. 𝟔
𝑷𝒚 = 𝟒, 𝟑𝟑𝟓𝒘
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
17
Thevenin-Norton Yöntemi Örnek
4Ω
5Ω
Örnek:
Yandaki şekillerdeki Vab gerilimi ile Iab akımlarını
bulunuz.
+
E1=25V-
5Ω
+
+
V1
Vab
-
-
3A
4Ω
5Ω
+
+
E1=25V-
5Ω
Iab
V2
3A
1.6Ω
Örnek:
a) Yandaki şekilde verilen devreye kaynak
dönüşümlerini uygulayarak V gerilimini bulunuz.
b) V gerilimi aşağıdaki tevenen açık devre gerilimi
ve norton kısa devre akımlarını bularak eşdeğer
devre üzerinden bulunuz.
c) 120V’luk kaynak devreye ne kadar güç aktarır?
20Ω
+
E1=120V
5Ω
+
E2=60V
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
+
6Ω
V
8Ω
36A
-
18
Örnek
Ix
30Ω
25Ω
Örnek: Yandaki devrede 30Ω’luk dirençten geçen akımı
Thevenin yöntemi ile bulunuz.
10Ω
E1=10V
+
-
10Ω
+
14kΩ
Örnek: Yandaki devrede 10kΩ’luk dirençten geçen akımı ve
harcadığı gücü
a) Thevenin yöntemi ile bulunuz.
b) Norton yöntemi ile bulunuz.
30 Ω
20.Ix
25kΩ
20kΩ
5kΩ
+
E1=10V-
12Ω I
x
14Ω
10A
Örnek: Yandaki devrede 20Ω’luk dirençten geçen akımı
Norton yöntemi ile bulunuz.
E1=80V +
40Ω
8Ω
Elektrik Mühendisliğinin Temelleri-Yrd. Doç. Dr. Yusuf SEVİM
10k Ω
12Ω
20 Ω
10.Ix +
6Ω