KONU TESTİ
ÖABT Lineer Cebir
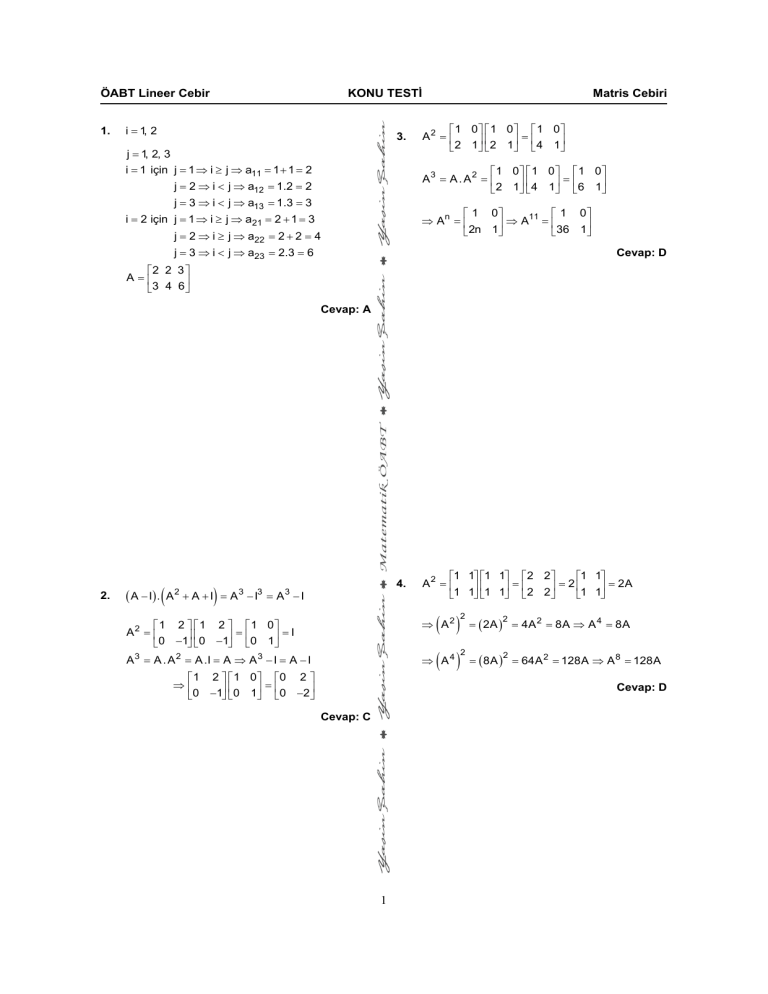
1.
Matris Cebiri
1 0 1 0 1 0
3. A 2 =
=
2 1 2 1 4 1
i = 1, 2
j = 1, 2, 3
i = 1 için j = 1 ⇒ i ≥ j ⇒ a11 = 1 + 1 = 2
1 0 1 0 1 0
=
A 3 A=
. A2
=
2 1 4 1 6 1
j = 2 ⇒ i < j ⇒ a12 = 1.2 = 2
j = 3 ⇒ i < j ⇒ a13 = 1.3 = 3
1 0
11 1 0
⇒=
An
⇒ A=
2n 1
36 1
i = 2 için j = 1 ⇒ i ≥ j ⇒ a21 = 2 + 1 = 3
j = 2 ⇒ i ≥ j ⇒ a22 = 2 + 2 = 4
j = 3 ⇒ i < j ⇒ a23 = 2.3 = 6
Cevap: D
2 2 3
A=
3 4 6
Cevap: A
2.
( A − I) . ( A
2
)
3
3
1 1 1 1 2 2
1 1
4.=
A2
=
=
2=
2A
1 1 1 1 2 2
1 1
3
+ A +I = A −I = A −I
( )
⇒ A2
1 2 1 2 1 0
A2
=
=
=
I
0 −1 0 −1 0 1
2
( )
A 3 = A . A 2 = A .I = A ⇒ A 3 − I = A − I
2
= ( 2A ) = 4A 2 = 8A ⇒ A 4 = 8A
⇒ A4 =
1 2 1 0 0 2
⇒
=
0 −1 0 1 0 −2
2
( 8A )2=
64A 2= 128A ⇒ A 8= 128A
Cevap: D
Cevap: C
1
KONU TESTİ
ÖABT Lineer Cebir
3 0 3 0
5. A 2 =
=
0 2 0 2
32
0
0
22
1 0 0 1 0 0
7. A 2 =
=
0 2 0 0 2 0
0 0 3 0 0 3
2
0 33
3 0 3
=
=
A 3 A=
. A2
0 2 0 22 0
3n
⇒=
An
0
0
A 20
⇒=
2n
320
0
Matris Cebiri
0
23
1 0 0
0 4 0
0 0 9
( )
⇒ iz = A 2 =1 + 4 + 9 =14
0
220
Cevap: B
Cevap: C
8.
A − B = AB ⇒ A = AB + B ⇒ A = ( A + Ι ) B
−1 1 1 0 0 1
=
A+Ι
+ =
1 0 0 1 1 1
6.
(A
−1
+A
)
2
A
=
= A −2 + A 2 + 2A −1. A
2
= A −2 + A 2 + 2 Ι ⇒ A −2 + A
=
(A
−1
+A
)
2
−1 1 0 1 a b
=
1 0 1 1 c d
(A + Ι)B ⇒
d
c
=
+
+
a
c
b
d
− 2Ι
2 4 2 4 2 0
⇒
=
A −2 + A 2
−
4 −2 4 −2 0 2
⇒ c =−1 a + c =
1 a =2
⇒
d=
1 b + d =0 b =−1
20 0 2 0 18 0
=
−
=
0 20 0 2 0 18
a b 2 −1
⇒
=
B =
c d −1 1
Cevap: D
Cevap: D
2
KONU TESTİ
ÖABT Lineer Cebir
9.
x1
x1x 2
x2
x 2 x3
x1x3
⇒
x1x 2 x3
x
x3 3
x1
x1x3
x 2
x1x 2
x1x 2 x3
11.
Matris Cebiri
1 3
x 0
= [a b ]
1
0 x
[ a b ] 3
⇒ [a + 3b 3a + b] =
[ax bx ]
x 2 x3
x1x 2 x3
⇒
+
a + 3b =
ax
3a + b =
bx
4 ( a + b ) = ( a + b ) x ⇒ x = 4 olmalıdır
c
x1x3 + x1x 2 + x 2 x3 = =
4
a
d
− =
x1x 2 x3 =
5
a
x1x3 + x1x 2 + x 2 x3 + 3x1x 2 x3 =
4 + 3.5 =
19
Cevap: E
Cevap: D
12. A A −1 = Ι olduğuna göre
1 −3 2 1 2 x 1 0 0
A A −1 = Ι ⇒ 1 1 −1 2 4 y = 0 1 0
−2 1 0 3 5 z 0 0 1
10.
1 0 x − 3y + 2z
1 0 0
⇒ 0 1 x + y − z =
⇒ 0 1 0
0 0 −2x + y
0 0 1
1 + 3 + 5 + ... + =
29 15.15
= 225
15 0
A =
1
+ 1 + ... + 1 =
15
0 225
15 tan e
⇒ 15 + 225 =
240
⇒ 2/
+
x − 3y + 2z =
0
x+y−z =
0
1
− 2x + y =
x = 1
y = 3 ⇒ ( x + y + z ) =1+ 3 + 4 = 8
z = 4
Cevap: E
Cevap: E
3
ÖABT Lineer Cebir
KONU TARAMA SINAVI - 1
1.
−2
3 0 0 3 0 0
4. A.A =
=
0 2 0 0 2 0
0 0 1 0 0 1
1 2] . A = [ 3 5 2]
[3
[2
2 1] . A = [0 2 1]
[ 3 1 2] . A = [ 3
+ [ −4 −4 −2] . A = [0
[3
[ −1 −3 0]. A =
5
Matris Cebiri
2]
−4 −2]
1 0]
3 0 0 9 0 0
A.A =
0 2 0 0 4 0
=
0 0 1 0 0 1
2
9 0 0
0 4 0
0 0 1
27 0 0
0 8 0
0 0 1
27 0 0 9 0 0
3 0 0 1 0 0
f ( A ) = 0 8 0 − 6 0 4 0 + 110 2 0 − 6 0 1 0
0 0 1 0 0 1
0 0 1 0 0 1
Cevap C
27 0 0 54 0 0 33 0 0 6 0 0
=0 8 0 − 0 24 0 + 0 22 0 − 0 6 0
0 0 1 0 0 6 0 0 11 0 0 6
2.
T
(B )=
(A + A )
T
T
0
0 0 0 0
−27
= 0 −16 0 =0 0 0
0
0 −5 0 0 0
(her iki tarafında transpozu
Cevap A
alınırsa)
T
B= A T + A elde edilir.
BT = B
1 2 1 2 1
Cevap B
5. A . A =
=
.
0 −1 0 −1 0
0
1
1 2 1 0 1 2
=
A . A 2 =
0 −1 0 1 0 −1
( )
A 2005 = A 2
1007
.A
1 0 1 2 1 2
= =
.
0 1 0 −1 0 −1
3.
2 −2
x
3 1 2 =
1
y
3
4 5 1
−4 3
z
Cevap E
2.3 + ( −2 ) .4
2.1 + ( −2 ) .5 2.2 + ( −2 ) .1 x
3.1 + 1.5
3.2 + 1.1 =
3.3 + 1.4
y
−4.3 + 3.4
z
− 4.1 + 3.5
−4.2 + 3.1
−2 −8 2 x
13 8 7 y
=
0
4 −5 z
6.
I, II, III
Cevap E
x=
8
z=
−2 y =
−5
x + y + z =−2 + 8 + ( −5 ) =1
Cevap D
4
ÖABT Lineer Cebir
7.
A 2 − 2A + I=
KONU TARAMA SINAVI - 1
( A − I) 2
1
=
3
8.
3 1
−
2 0
0
1
2
1
1
=
a11 =
1
1
0
=
a12 =
2
1
0
=
a13 =
3
2
2
=
a21 =
1
2
0 3
=
3 1
0 3 0
=
3 1 3
3
9
=
3
10
Matris Cebiri
3
1
2
1
=
a22 =
2
2
0
=
a23 =
3
Cevap C
3
3
=
a31 =
1
3
1
=
a32 =
2
3
1
=
a33 =
3
1 0 0
A = 2 1 0
3 1 1
1+ 0 + 0 + 2 + 1+ 0 + 3 + 1+ 1 =
9
Cevap C
5
KONU TESTİ
ÖABT Lineer Cebir
1.
4.
1 0
1 0
2 1
S2 → S2 + 2S1
S2 ↔ S1
0
1
2
1
1 0
Elementer İşlemler
a şıkkı haricindeki tüm şıklar bir elementer işlem
yapılarak birim matris elde edilebilir.
Fakat a şıkkında en az iki elementer işlem
yapmak gerekir. Bu nedenle a şıkkındaki matris
2 işlem yapılarak elde edilmiştir.
elementer matris değildir.
Cevap: B
Cevap: A
2.
1 0 0
0 0 1 matrisinde 3. Satırdaki 1 2. Satırda
0 1 2
ki 1 in solunda kaldığı için eşelon matris olamaz.
5.
I, II, III
Cevap: E
Cevap: E
3.
b şıkkındaki matris dışında hepsi eşelondur.
Bu eşelon matrisler içinden sadece c şıkkanda
6.
matriste her satırın ilk 1 elemanının bulunduğu
I, II, III
Cevap: E
sütundaki diğer elemanlar sıfırdır.
Cevap: C
7
ÖABT Lineer Cebir
1.
KONU TARAMA SINAVI - 2
1 0
0 1
9 1
1+ ∫ 2
0 1 ∫
∫ 1 + ∫ 2 + 9∫ 2
1 0 1 0
9 1
2 → ∫ 12
∫
3 0
4.
Elementer İşlemler
1 0 0
0 0 1 matrisinde tek satır işlemi olduğu
0 1 0
için elementer bir matristir. (2. satırla 3. satır yer
değiştirmiş)
Cevap C
Cevap A
2.
0 1 2
Eşolon olma şartını 0 0 1 matrisi sağla0 0 0
5.
II. öncülün doğrusu,
Bir kare matrisinin tersinin olması için gerek ve
yeter şart bu matrisin birim matrise satır denk
maktadır.
olmasıdır.
Cevap D
Cevap C
3.
1 0 0
0 1 0 matrisinde a32 elemanı sıfır olma
0 1 1
6.
I, II, III
Cevap E
lıydı.
Cevap D
8
KONU TESTİ
ÖABT Lineer Cebir
Determinantlar
cos2 15 sin2 15
3. =
det A
=
cos4 15 − sin4 15
sin2 15 cos2 15
1.
)
)(
(
=
cos2 15 − sin2 15 cos2 15 + sin2 15
1
= cos2 15 − sin2 15 = cos 30
=
a
b
c
= = = 2R
sin A sinB sin C
3
2
Cevap: C
A matrisinin 1. ve 2. satırı orantılı olduğu için
det A = 0 dır.
Cevap: A
2.
1
1
2013 2014 2015 S1 → S1 − S2 1
2012 2013 2014
A = 2012 2013 2014
2011 2012 2013
2011 2012 2013
4.
⇒ ( ln x ) − 6 + 7 − 2ln x =
0
2
S 2 → S 2 − S3 1
1
1
1
1
1 = AI
2011 2012 2013
⇒ ( ln x ) − 2ln x + 1 =
0
2
⇒ ( ln x − 1) = 0 ⇒ ln x − 1 = 0
2
⇒ ln x =
1
⇒x=
e
det A = det AI ve AI matrisinin 1. ve 2. satırları
eşit
olduğundan
det AI = 0
ln x 3 7 2
0
+
=
2 ln x ln x 1
dolayısıyla
Cevap: D
det A = 0 dır.
Cevap: C
9
KONU TESTİ
ÖABT Lineer Cebir
5.
A matrisinin determinantını 2. satıra göre he-
7.
saplarsak,
2 −1 3 4
2 −1 4
2+3
0 0 2 0 =
det A =
2 ( −1)
3 5 −2
3 5 1 −2
0 0 5
0 0 4 5
Determinantlar
−b
a b
−1 d
=
B
⇒ B = −
c d
c a
−2
1 2
−1 5
A=
⇒ A = −
3 5
3 1
5 −2
−1
−1
det A =
A −1 =
−3 1
11
3. satıra göre hesaplarsak,
2 −1
= 5 (10 + 3 )
3 5
= 65. ( −2 )
Cevap: A
( −2 ) .5 ( −1)3+3
2
−1 −5
= 130A
=
3 − 1
Cevap: A
6.
x1 x 2 x3
1 2 3 = 0
3 2 1
8.
A matrisinin tersi olmadığına göre det A = 0
olmalıdır. A matrisinin 3. sütuna göre determi-
⇒ x1 ( 2 − 6 ) − x 2 (1 − 9 ) + x3 ( 2 − 6 ) =
0
nantını hesaplarsak,
⇒ −4x1 + 8x 2 − 4x3 =0
2 −1 0
8 2 x =
0
− x4 + 1( 4 + 8 ) =
4 0 1
⇒ 12 − 4x =0 ⇒ 12 =4x
⇒x=
3 olmalıdır.
⇒ −4 ( x1 + x 2 + x3 ) = −12x 2
⇒ x1 + x 2 + x3 =
3x 2
b 3
= =
3
a 1
⇒ 3= 3x 2 ⇒ x 2= 1
⇒ x1 + x 2 + x3 =
−
⇒ 1 3 − 3.1 2+ m.1 − 3 =
0
⇒m=
5
Cevap: E
Cevap: E
10
KONU TESTİ
ÖABT Lineer Cebir
9.
Bir matrisin tersinin olmaması için gerek ve
Determinantlar
1
11. A −=
yeter şart determinantının sıfır olmasıdır.
3 4 2
A şıkkındaki 0 5 0 matrisinin determinantı
6 1 4
1
1
ek ( A ) ⇒ A A −=
ek ( A )
A
⇒ A A . A −1 =
A .ek ( A )
⇒ A Ι =A .ek ( A )
det =
A
3 4 2
2+ 2
5 ( −1)
( 3.4 − 2.6 ) =0
0 5 0 =
6 1 4
2 0 −1
A
= 3 2 1
4 1 −3
1. satıra göre
hesaplanırsa
2. sütuna göre
hesaplanırsa
=2 ( −6 − 1) − 1( 3 − 8 ) =−14 + 5 =−9
olduğundan bu matrisin tersi yoktur.
⇒ A.ek ( A ) = A . Ι = −9 Ι
Cevap: A
Cevap: E
a b
d −b
10. A =
⇒ ek ( A ) = −c a
c d
d −b a b
ek ( A ) =
A⇒
=
−c a c d
a=d
⇒
−b = b ve − c = c ⇒ b = c = 0
a 0
Buna göre 2 x 2 tipindeki bir matris
0 a
12. A 2 + A − Ι = 0 ⇒ A 2 + A = Ι
formunda olursa ek ( A ) = A olur.
⇒ A (A + Ι) = Ι
2 0
Bu forma uyan şıklardaki tek matris
0 2
⇒ det A ( A + Ι =
) det Ι
⇒ det A .det ( A + =
Ι ) det Ι
⇒ 2.det ( A + Ι ) =1
matrisidir.
⇒ det ( A + Ι ) =
Cevap: A
1
2
Cevap: B
11
KONU TESTİ
ÖABT Lineer Cebir
13. Bu soruda determinantın açılımından gelecek
Determinantlar
15. A 2 + A − Ι = 0 ⇒ A 2 + A = Ι
ifadelere ters dönüşüm formüllerini uygulamak
⇒ A (A + Ι) = Ι
yerine değer vererek yapmak daha pratik bir
⇒ det A .det ( A + =
Ι ) det Ι
yoldur.
⇒ det A .det ( A + Ι ) =1
=
x 0,=
y 0,=
z 270o alınırsa
≠0
sin x = 0, sin y = 0, sin z = −1 olur.
sin x sin y
1
=
sin
x
1
sin
z
sin y sin z
1
≠0
det A ≠ 0 olduğundan rank A = n
1 0 0
1
0
0 1 −=
0 −1 1
A2 + A − Ι = 0 ⇒ A ( A + Ι ) = Ι
⇒
Ι ) A −1 Ι
A −1A ( A +=
Ι
⇒ A + Ι = A −1
2. ve 3. satır
orantılı olduğundan
det er min antın
değeri sıfırdır.
A2 + A − Ι = 0 ⇒ A2 = Ι − A
⇒ A . A 2= A ( Ι − A )
⇒ A 3 =A − A 2
Cevap: C
⇒ A 3= A − ( Ι − A )
3
⇒ A=
2A − Ι
Cevap: E
−1 −a −b
14. det A= a −1 −c
b
c −1
(
)
=−1 1 + c 2 + a ( −a + bc ) − b ( ac + b )
1 1 1 1
1 1 1
1 1 1
x a 0 0
=
16.
− x 0 b 0 + a x b 0
x 0 b 0
0 0 c
x 0 c
x 0 0 c
3. satıra
3. satıra
=−1 − c 2 − a2 + abc − abc − b2
(
)
=−1 − a2 + b2 + c 2 ≠ 0
2. satıra göre
açılırsa
≥0
⇒ det A ≠ 0 olduğundan rank A = 3 ve düzgün
göre
göre
=
− x b c + a ( − xb + c ( b − x ) ) =
0
matristir.
⇒ − xbc − xab + abc − xac =0
Düzgün matris → Tersi olan matris
1 1 1
⇒=
1 x + +
a b c
1 1 1 1
⇒ = + +
x a b c
Bir matrisin ters simetrik olması için esas köşegen elemanlarının sıfır olması gerekir. Yani bu
matris ters simetrik değildir.
Cevap: A
Cevap: D
12
KONU TESTİ
ÖABT Lineer Cebir
17. A =A −1 ⇒ det A =det A −1
⇒ det A =
( det A )
Determinantlar
18. A −1 =
−1
1
ek A ⇒ det A . A −1 = ek A
det A
⇒ det A . A . A −1 =
A .ek A
⇒ ( det A ) =
±1
1 ⇒ det A =
2
A −1 =
Ι
⇒ det A . Ι =A .ek A
1
ek A
A
⇒ AA
−1
=
ek A ⇒ A A
⇒ A
n
−1
A −1=
=ek A
1
n 1
ek A ⇒ ek A = A A −1 ⇒ ek A = A
A
A
n −1
A
⇒ ek A =
1
=
ek A
A
−1
n −1
⇒ A
=
ek A
( ek A )−1 =
≠0
olduğundan rank ( ek A ) = n
)
−1
1
= A... ( * )
A
1
ek ( ek A )
1
ek ( ek A ) ... ( * * )
ek A
( * ) ve ( * * ) dan
A ve B ortagonal ise
1
A
=
A
A T = A −1
T
BT . A T
⇒ ( AB ) =
BT = B−1
1
1
ek ( ek A=
)⇒ A
ek A
A
⇒ A
= B−1. A −1
= ( AB )
(
ek A =A A −1 ⇒ ( ek A ) = A A −1
−1
n−2
A
n −1
A=
ek ( ek A )
n = 2 için II. Öncül doğru olur. Daima doğru
olmaz.
Olduğundan AB matrisi de ortagonaldir.
k ∈ , det ( k.A ) =
k n det A →
teorem
gereği
doğrudur.
Cevap: D
Cevap: C
13
ÖABT Lineer Cebir
1.
KONU TARAMA SINAVI - 3
II. yol
1 2 3
A= 4 5 6
7 8 9
1
4
2
5
1
.Ek A
A
A −1 =
3
6
A.A −1 =
(1.5.9 + 4.8.3 + 7.2.6 ) − ( 3.5.7 + 6.8.1 + 9.2.4 )
= ( 45 + 96 + 94 ) − (105 + 48 + 72 )
= ( 225 ) − ( 225 ) = 0
=
1
.A.E.kA
A
A .I = A.EkA
A .I = A.EkA
n
A . I = A . EkA
Cevap A
A
2.
Determinantlar
1
n −1
= EkA
3 2 0
−1 1 −2
A=
1 0 3
3 2 0
det A =−1 1 −2 =11
1 0 3
1 −2
a11 =
=
3
( −1)1+1
0 3
−1 −2
a12 =
1
=
( −1)1+ 2
1 3
−1 1
a13 =
=
−1
( −1)1+3
1 0
3 −1
det (EkA ) = ( det A )
= 112
2 0
a21 =
=
−6
( −1)
0 3
2 +1
= 121
Cevap E
3 0
a22 =
9
=
( −1)2+ 2
1 3
3 2
a23 =
=
2
( −1)2+3
1 0
2 0
a31 =
=
−4
( −1)3+1
1 −2
3 0
a32 =
=
6
( −1)3+ 2
−1 −2
3 2
a33 =
5
=
( −1)3+3
−1 1
3.
rank ( A ) < 3 için A =
0 olmalı
T
3 1 −1
3 −6 −4
6 9 2
1 9 6 Ek A
−
=
( )
=
−4 6 5
−1 2 5
3 −6 −4
det (Ek ( A ) ) = 1
−1
3
1
9
2
6
5
−6
9
−4
6
=
A
5
2
x
3
4
−1
( 5.3 ( −2) + 2.1.4 + ( −1) .x. ( −1) )
− ( 4.3 ( −1) + ( −1) .1.5 + ( −2 ) .x.2 ) =0
=
= ( −30 + 8 + x ) − ( −12 − 5 − 4x ) = 0
( 3.9.5 + 1.2. ( −4 ) + ( −1) . ( −6 ) . ( 6 ) ) −
( −4.9. ( −1) + 6.2.3 + 5. ( −6 ) .1)
=−
( 24 + x ) − (17 + 4x ) =0
=
=−24 + x + 17 + 4x =0
5x = 5
x =1
( 235 − 8 + 36 ) − ( 36 + 36 − 30 )
=
5 x 4
2 3 −1
−1 1 −2
= 163 − 42 = 121
Cevap D
14
ÖABT Lineer Cebir
4.
A −1 =
KONU TARAMA SINAVI - 3
1 d −b
ad − bc −c a
7.
Determinantlar
Ters simetrik ise A T = − A olmalı I. öncül doğrudur.
5 −2 −5 2
A −1 =
−1
=
−3 1 3 −1
II) A T = − A
AT =
Cevap A
( −1)n
A
III) n tek ise
AT = A
AT =
−A
( −1) A ⇒ A T =
n
2 A =0
A =0
Cevap E
5.
rankA = 3 olduğundan det A ≠ 0 dır.
A 2 = 2A
A
2
2
8.
= 2A
3
(
n
A
2=
. A k.A k . A
=
A −1 + B.Ek.A =
0
B.Ek ( A ) = − A −1
)
B.Ek ( A ) .A = − A −1.A
2
A −8 A =
0
B.A = −Ι
A ( A − 8 ) =0 ⇒ A =8
B = −3 Ι
B =
( −3 ) . Ι
2
Cevap D
B = 9.1
B =9
Cevap E
6.
( )
I) det A −1 = ( det A )
−1
olmalıydı dolayısıyla I.
öncül yanlıştır.
II) Determinantta böyle bir özellik yok
BAB−1 = B . A . B−1
III)
= B.A.
1
B
= A olur.
Cevap B
15
ÖABT Lineer Cebir
1.
KONU TESTİ
2. ve 3. denklemler taraf tarafa toplanırsa
3.
Lineer Denklem Sistemleri
A matrisi üst üçgensel bir matristir. Üçgen matrislerin determinantı esas köşegen üzerindeki
5a + c =
10
elemanların çarpımına eşittir.
2. denklemin iki katı ile 1. denklem toplanırsa
=
=
det A 1.2.3.
4.5 5! ( b şıkkı doğru )
7a + 5c =
14
det A ≠ 0 olduğundan
−5 / 5a + c =
10 −25a − 5c =
− 50
−36
− 18a =
7a + 5c =
14 7a + 5c =
14
rank A = 5 ( c şıkkı doğru )
A −1 =
=
a 2,=
c 0
1
.ek ( A )
A
A −1 ⇔ A ≠ 0 olsun ( a şıkkı doğru )
İse a.b.c
= 2.b.0
= 0
iz ( A ) → esas köşegendeki elemanların topla-
Cevap: C
mıdır.
iz ( A ) = 1 + 2 + 3 + 4 + 5 = 15 ( e şıkkı doğru )
Ax = 0 denklem sisteminde A ≠ 0 ise
rank = 5 olur ve dolayısıyla sistemin tek çözümü aşikar çözümdür.
Cevap: D
2.
4.
rank A = 3
n bilinmeyen sayısı olmak üzere,
=
rank A rank
=
[ A : B] r
olursa denklem sisteminin tek çözümü aşıkar
çözümdür.
n = r ise tek çözüm vardır.
rank A= r < 3 ise
r < n ise ( n − r ) parametreye bağlı sonsuz çö-
Denklem sisteminin 3-r parametreye bağlı son-
züm vardır.
suz çözümü olur.
rank A ≠ rank [ A : B]
Bu soruda aşıkar olmayan çözümlerden bahset-
İse sistemin çözümü yoktur.
tiğine göre rank A ≠ 3 olmalı yani A = 0 olma-
1 −1 1 : 1
=
[ A : B] 1 0 a : −2
1 a 1 : 3
lıdır.
1
−1 −1
A =1
2
3 =−3 + 3a =0 → a =1 olmalı
3
0
a
1
0
0
−1
1
: 1
a − 1 : −3
a + 1 0 : 2
1
0 olmalı
rank A ≠ rank [ A : B] olması için a + 1 =
yani a = −1
Cevap: A
Cevap: B
16
KONU TESTİ
ÖABT Lineer Cebir
6.
5.
1 2 −1 : −1
[ A : B] =
2 −1 3 : 2
3 1 2 : 1
Lineer Denklem Sistemleri
A matrisi düzgün (tersi olan) matris olduğuna
göre det A ≠ 0 olmalıdır.
1 2 −1 : −1
0 −5 5 : 4
0 −5 5 : 4
1 2 −1 : −1
0 −5 5 : 4
0 0 0 : 0
det A = a.d − b.c ≠ 0
( a şıkkı doğru )
Teorem: Bir kare matrisin tersinir olması için
gerek ve yeter şart bu matrisin birimin matrise
satır denk olmasıdır.
A tersinir bir matris olduğundan I2 birim matrisi-
⇒ rank [ A : B] =
rank A =
2
ne satır denktir.
(b şıkkı doğru)
Bilinmeyen sayısı 3 olduğundan
Teorem: Tersinir her matris elementer matrisle-
3−2 =
1 parametreye bağlı sonsuz çözüm var-
rin çarpımı şeklinde yazılabilir. (c şıkkı doğru)
dır.
det A ≠ 0 olduğundan rank A =
2 dir.
Cevap: D
(e şıkkı doğru)
Ax = 0 homojen lineer denklem sisteminde,
rank A= 2= bilinmeyen sayısı
olduğundan
sistemin sadece aşikar çözümü vardır.
(d şıkkı yanlış)
Cevap: D
17
ÖABT Lineer Cebir
1.
KONU TARAMA SINAVI - 4
2 denklemi ( - ) ile çarpıp 3 denklem taraf tarafa
3.
toplanırsa
n = r ise tek çözüm vardır.
− 2x + y − 3z =−4
r < n ise ( n − r ) parametreye bağlı sonsuz çö-
x + 2y − z =
1
3
ax + 3z =
9 ⇒z=
züm vardır.
1: a 1 2
1: a
1 2 1: a 1 2
1
1
0
:
b
0
−
1
−
1:
b
−
a
0
−
1
−
1:
b
−
a
3 1 −2 : c 0 −5 −5 : c − 3a 0 0 0 : c − 5b + 2a
1. ve 2. denklemin taraf tarafa toplanırsa
+
n bilinmeyen sayısı olmak üzere,
=
rankA rank
=
[ A : B] r
x−y+z =
4
+
Lineer Denklem Sistemleri
x−y+z =
4
2x + y − 3z =−4
3x − 2z =
0
c − 5b + 2a =
0
=
3x 2z
=
3x 6
x=2
=
x 2,=
y 1,=
z 3
c + 2a =
5b
x+y+z =
6
Cevap B
Cevap E
2.
rank A = 3
olursa denklem sisteminin tek çözümü aşikar
çözümdür.
rank A = r < 3 ise
denklem sisteminin 3 – r parametreye bağlı
sonsuz çözümü olur.
Bu soruda aşikar olmayan çözümlerden bahsettiğine göre rankA ≠ 3 olmalı yani
4.
* A matrisi alt üçgensel bir matristir. Üçgen
matrislerin determinantı esas köşegen üzerin-
A = 0 olmalıdır.
deki elemanların çarpımına eşittir. (I. öncül doğ−1
ru)
1 = 0 ⇒ 1. ( −m ) − 1. ( −1) + ( −1) . ( 2m − 1) = 0
* A ≠ 0 olduğu için tersinir bir matristir. (II. ön1 m 0
1
A = 2
1
1
−m + 1 − 2m + 1 =0
−3m =
−2
m=
cül doğru)
* A ≠ 0 olduğu için rank A = 3 tür. (III. öncül
2
3
doğru)
Cevap D
Cevap E
18
ÖABT Lineer Cebir
5.
KONU TARAMA SINAVI - 4
A matrisi düzgün bir matris ise A ≠ 0 dır.
6.
Lineer Denklem Sistemleri
I, II, III öncülleri elemanter işlem özelliğini sağlar.
Teorem: Tersinir her matris elemanter matrisleCevap C
rin çarpımı şeklinde yazılabilir. (I. öncül doğru)
Teorem: Bir kare matrisin tersinir olması için gerek ve yeter şart bu matrisin birim matrise satır
denk olmasıdır.
A tersinir bir matris olduğundan Ι3 birim matrisine satır denktir. (II. Öncül doğru)
Ax = B lineer denklem sisteminde,
= 3 ise,
rank [ =
A : B] rankA
n = r ise lineer denklem sisteminin tek çözümü
vardır. (III. Öncül yanlış)
Cevap D
19
KONU TESTİ
ÖABT Lineer Cebir
1.
∅ ≠U⊂ V
4.
i) Ov ∈ U
ii) ∀u1, u2 ∈ U için u1 + u2 ∈ U
Vektör Uzayları
1 2 1 2
A=
3 6 0 0
rankA = 1 olduğundan
çözüm uzayının boyutu 1 dir.
iii) ∀a ∈ F ve ∀u ∈ U, a.u ∈ U
Cevap: B
şıkları incelediğimizde,
A) U/W, V nin bir alt uzayı değildir. Fark işlemi
sonucu 0 kalmaz dolayısıyla i) sağlamaz.
5.
C ve E şıklarında sıfır elemanı çıkartıldığı için i)
maddeyi sağlamaz.
boy
=1
2
boy
= 2 boyFn = n dir.
boy
=1
boy
=2
Soruda daima doğru olanı sorduğu için D şıkkı
sağlamayabilir.
Cevap: B
( a,b )
= a (1,0 ) + b ( 0,1) doğrudur.
= {(1,0 ) , ( 0,1)}
=
+:b
boy
2 için a=
2.
A ve B şıkları 0 vektörünü barındırdığı için lineer
bağımlıdır. C şıkkında ise birbirinin skalar katı
olan vektörler lineer bağımlıdır. D şıkkında hem
0 var hem de birbirinin katı olan ifadeler yer almakta olduğu için lineer bağımlıdır.
Cevap E
Cevap: E
6.
B ve E şıkkındaki vektörler birbirinin skalar katı
olduğu için lineer bağımlıdır.
C ve D şıkları ise (0, 0) vektörlerini bulundurdu
ğu için lineer bağımlıdır.
3.
2 nin boyutu iki lineer bağımsız eleman sayısı
da iki olduğu için
i) Ov ∈ U
ii) ∀u1, u2 ∈ U için u1 + u2 ∈ U
{( 0,2) , (1,1)} → 2
iii) ∀a ∈ F, ∀u ∈ U, a.u ∈ U
yi geçer.
Cevap A
I) (0, 0) şartını sağlamadığından dolayı alt vektör uzayı değildir.
II) i) (0, 0) sağlar fakat ( 2,0 ) + ( 0,3 ) =
( 2,3 ) olur.
ii) şart sağlanmaz.
III) i) (0, 0) sağar. ii) ( −2,3 ) + ( −5, 4 ) = ( −7,7 )
sağlar
iii) −4 ( −3,1)=
(12, −4 )
7.
olur sağlanmaz. Çünkü
w, (0, 2) tarafından gerilmez, w iki boyutlu vektör uzayıdır.
(0, 2) bir boyutlu olduğu için w uzayını germez.
x ≤ 0 değil.
Alt vektör uzayı değildir.
IV) i) (0, 0) sağlar. ii) ( 0,0 ) + ( 0,0 ) =
( 0,0 )
Cevap A
iii) 4 ( 0,0 ) = ( 0,0 )
Her üç şartta sağlandığından alt vektör uzayıdır.
Cevap: B
8.
I, II, III
Cevap E
20
KONU TESTİ
ÖABT Lineer Cebir
9.
I. öncül doğrudur.
Vektör Uzayları
11. I) u + v ≤ u + v
II. öncül tanımla çalışır.
(üçgen eşitsizliği) olmalıydı
(I. öncül yanlış)
III. boyw = 0 da bilir. Örneğin sıfır vektörünün
sıfırdır.
II) u + v
Verilen yargılardan yalnız I daima doğrudur.
2
2
(
+ u − w= 2 u
2
+ v
2
)
(II. Öncül
doğru)
Cevap A
III) u,u ≤ u . v olmalıydı. (III. öncül yanlış)
Cevap B
10. I) {u, 3u} 2 nin bazıdır.
II)
{( 0,0 ) , w} ( 0,0 )
12. I)
vektörünü bulundurduğun-
=
=
0,1) , z (1,2 )
(1,0
) , v ( 2,1
) , w (=
ün bir bazıdır.
Standart bazı
II) Her vektörün
ortogonaldir.
dan lineer bağımlıdır. Dolayısıyla 2 nin bazı
değildir.
III) u
=
{(1,0,0 )( 0,1,0 )( 0,0,1)} + 3
normu
1
olduğu
için
III) boyw = 0 da olabilir. Örneğin sıfır vektörünün sıfırdır.
şek-
linde seçersek;
Verilen yargılardan yalnız I daima doğrudur.
vektörler birbirinin skalar
u + w= (1,0 ) + ( 0,1=) (1,1)
2
katı olduğu için yi
v +=
z ( 2,1) + (1,2=) ( 3,3 )
germez.
Cevap A
III. öncül daima doğru değildir.
Cevap A
21
ÖABT Lineer Cebir
1.
Vektör Uzayları
KONU TARAMA SINAVI - 5
I ve III öncül daima doğrudur. II öncül daima
3.
doğru değildir.
A şıkkı (0, 0, 0) dan dolayı lineer bağımlıdır.
B şıkkındaki vektörler birbirinin sklar katıdır.
Dolayısıyla lineer bağımlıdır.
Cevap D
C şıkkındaki vektörler lineer bağımsız fakat
boyut iki olduğu için 3 uzayını germez.
D şıkkında verilen vektörler lineer bağımsız
olduğu için 3 uzayını geçer.
E şkkı lineer kombinasyon olarak yazılabilir
lineer bağımlıdır.
Cevap D
2.
A) y = x + z → ( 0,0 ) sağlamaz alt uzayı değildir.
B) x + y = z → ( 0,0 ) sağlamaz alt uzayı değildir.
D) y= 2 → ( 0,0 ) sağlamaz alt uzayı değildir.
E) x =−1 → ( 0,0 ) sağlamaz alt uzayı değildir.
C) x =
0 → ( a, y ) → i) ( 0,0 ) sağlar
ii) ( 0,3 )
+
( 0,2 )
( 0,5 )
4.
sağlandı.
v1 = {( a,a,0 )}
{( 0,b,c )}
{( a,a + b,c )}
{a (1,0,0 ) + ( a + b )( 0,1,0 ) + c ( 0,0,1)}
v 2=
iii) 2 ( 0,3 ) = ( 0,0 ) sağladı.
v1 + v 2=
lineer bağımsız üç vektör olduğundan
Dolayısıyla x = 0 2 nin alt uzayıdır.
boy ( v1 + v 2 ) =
3 tür.
Cevap C
Cevap D
22
KONU TESTİ
ÖABT Lineer Cebir
Lineer Dönüşümler
5.
1 0
1
1. T 0 1 −1
=
1 −1 1
+
Cevap: B
+
−
T ( −1,2 ) =
( 5,2)
2
T ( 0,1) = ( 3,0 )
T (1, −2 ) = ( −5, −2 )
T ( 0,2 ) = ( 6,0 )
T (1,0=
)
(1, −2)
(1, −2 )
T (1,0=
)
T ( 0,1) = ( 3,0 )
1 3
−
2 0
5 0 5
2. =
T 2 −1 2
5 3 −5
Cevap: A
det T = 0 olduğundan rank T < 3 tür.
5 0
2 −1 ≠ 0 olduğundan rank T = 2
Cevap: C
6.
( A,B ) ∈ M2 ( )
i) T ( A + B ) = ( A + B ) − ( A + B )
T
3.
= A T − A + BT − B
x+z =
0
T ( A ) + T (B )
x − 2y =
0
ÇekT =
=
ii) k ∈
{( 2t, t, −2t ) t ∈ }
{t ( 2,1, −2) t ∈ }
{( 2,1, −2)}
T=
(k.A )
(k.A )T − k.A
(
= k AT − A
)
boyÇekT =
1
T lineer dönüşümdür.
3
boy
=
boyÇekT + BoyΙmT
0 0
II) T ( A ) =
3= 1 + 2
0 0
Cevap: B
a b
A=
c d
AT = A
4.
Verilen şıkları T ( x, y=
)
( x, y, − x + y )
a c a b a x
=
=
b d c d x d
b= c= x bilinmeyen sayısı 3 olduğu için
çekirdek uzayın boyutu 3 tür.
lineer dö-
III) BoyM2=
( ) boyÇekT + boyΙmT
nüşümün de yerine yazarsak,
( 3,1, −2=) ( x, y, − x + y )
i)
için sağlar.
x=3
y =1
22
3 +
=
boyΙmT =
1
?
Cevap: E
Cevap: D
23
ÖABT Lineer Cebir
1.
( 0, −1)
T (1,0=
)
T ( 0,1) = (1,0 )
Lineer Dönüşümler
KONU TARAMA SINAVI - 6
0 1
−
1 0
4.
T ( e1 + e2 )= T ( e1 ) + T ( e2 )
2
− =
1
0
Cevap A
3
+
1 T ( e2 )
1
−1
T ( e2 ) = −2
−1
T ( e1 − e2 − e3=
) T ( e1) + T ( e2 ) − T ( e3 )
0
=
1
1
2.
4
T ( e3 ) = 2
1
3 −1 4
=
T 1 −2 2
1 −1 1
T ( x, y ) = ( 2x + 3y, − x )
T ( 2, −1=
)
=
( 2.2 + 3. ( −1) , − 2)
(1, −2 )
Cevap E
Cevap C
3.
3 −1
− − −
1 2 T ( e3 )
1 −1
Bu soruda şıklardaki ifadeleri
T ( x, y, z ) =x + 3y + 2z lineer dönüşümünde ya-
zıldığında
x + 3y + 2z =
0
sağlamalı
A şıkkı yazıldığında
T (1,1,1) = 1 + 3 + 2 ≠ 0 olduğundan çek(T) nin
elemanı değildir. Diğer bütün şıklar sağlar.
Cevap A
24
ÖABT Lineer Cebir
1.
det ( A − ∂I) =
KONU TESTİ
Özdeğerler-Özvektörler ve Köşegenleştirme
−1 − ∂
3
= ∂2 − ∂ − 5
1
2−∂
6.
Cevap D
det
=
( A − ∂ I)
2−∂
1
= 0
2
3−∂
⇒ ∂ 2 − 5∂ + 4 = 0
∂=
∂=
4
1 1
2
∂1 =1 için
2.
( 2 − ∂ ) x1 + x2 = 0 x1 + x2 =
0
x1 = x 2
2x1 + ( 3 − ∂ ) x 2 = 0
izA = 1 + 2 + 3 = 6
1
x1 =
−1
∂2 =
4 için
Cevap D
1
−2x1 + x 2 =0 ⇒ x 2 =
2
3.
Cevap B
3 − 1 −12
4
−2
det (=
A − ∂I)
a
0 − 1=
0
a
5
a −1
7.
2 ( −a + 1 + 10 ) + 12 ( a ( a − 1) + 2a ) + 4 ( 5a + a ) =0
6a2 + 17a + 11 =0 ⇒ a =−1∈ , a =−
1 1
A=
6 2
1− ∂
2
= 0 ⇒ (1 − ∂ ) . ( 2 − ∂ ) − 6= 0
6 2−∂
11
6
∂ 2 − 3∂ − 4= 0 ⇒ ( ∂ − 4 ) . ( ∂ + 1)= 0
=
∂1 1 ve =
∂2 4
Cevap B
(1 − ∂ ) x1 + x2 = 0
1
P1 =
−2
1
P2 =
3
4.
4 2 4 2 18 18
2 2
1 1
1 3 −1
=
=
=
A 2 A.A
=
9 =
P =
P−1
1
5
1
5
9
27
,
1 3
2
3
−
5 2 1
1 3 −1 1 1 1 1 −1 0
−1
2−∂
2
D P=
.A.P
=
.
.=
=
det ( A − ∂I) 9= 0
5 2 1 6 2 −2 3 0 4
1
3−∂
yada
9 6 − 2∂ − 3∂ + ∂ 2 − 2 =0
4 0
0 1
0
9 ∂ 2 − 5∂ + 4=
∂=
9,
∂
=
36
1
2
−
Cevap B
Cevap C
8.
I – II – III
Cevap E
5.
3 −1
T=
−1 2
9.
I – II – III
det T = 5
10. I – II – III
Cevap E
Cevap E
Cevap E
25
KONU TARAMA SINAVI - 7 Özdeğerler-Özvektörler ve Köşegenleştirme
ÖABT Lineer Cebir
1.
=
det
( A − λT )
1− λ
2
= 0
4
3−λ
(1 − λ )( 3 − λ ) − 8=
4.
Verilen öncüllerin her biri bir teoremdir.
Cevap E
0 ⇒ 3 − λ − 3λ + λ 2 − 8= 0
λ 2 − 4λ − 5 = 0
λ
+1
λ
−5
λ = −1, λ = 5 özdeğerleri
Cevap E
2.
5.
1− λ
0
2
− λT )
−3
det ( A=
0
2−λ =
0
3
1
4−λ
A 2 = 0 ise nilpotent matris
I. ve II. öncüller doğrudur.
(1 − λ ) ( ( 2 − λ )( 4 − λ ) + 3 ) − 6 ( 2 − λ ) = 0
(1 − λ ) ( 8 − 2λ − 4λ + λ
2
A 2 = A idempotent matris
Cevap C
)
+ 3 − 12 + 6λ = 0
(1 − λ ) ( λ2 − 6λ + 11) − 12 + 6λ =0
−λ3 − 11λ + 7λ 2 − 1 =0
Cevap A
2 0 2 0 4 0
3. A.A =
=
3 1 3 1 9 1
2 0 4 0 8 0
=
A.A 2 =
3 1 9 1 21 1
8−λ
0
det
=
( A − λT ) = 0
21 1 − λ
( 8 − λ )(1 − λ ) = 0
=
λ 1, =
λ 8
Cevap E
26
ÖABT Lineer Cebir
GENEL TARAMA SINAVI
1 0 1 0 1 0
1. A.A =
=
3 −1 3 −1 0 1
(A )
2
1007
6.
A
A
1 0
=
0 1
2
= 32. A
2
=9 A
2
A −9 A =
0
A ( A − 9) =
0
Cevap A
A ≠0
A =
9
Cevap E
2 0 2 0 4 0
2. A.A =
=
0 3 0 3 0 9
2 0 4 0 8 0
=
A.A 2 =
0 3 0 9 0 27
16 0
A4 =
0 81
7.
1 x x2
1
x
x2
=
A 1 y y 2 0 y − x y 2 − x 2 ( y − x )( z − x )
1 z z2
0 z − x z2 − x 2
1 x x2
1 x
x2
0 1 y + x ( y − x).(z − x) 0 1
y+x
0 1 z+x
0 0 z+x−y−x
16 + 0 + 0 + 81 =
97
1 x x2
A
( y − x )( z − x ) 0 1 y + x ( y − x )( z − x )( z − y ) =
0 0 z−y
Cevap D
yada A =
( x − y )( x − z )( z − y )
Cevap D
3.
I ve II öncül doğrudur.
III. öncüldeki gibi bir özellik yoktur.
8.
Cevap C
A = −1
=
A −1
5 7
1 −5 −7
⇒ A −1
=
−1 2 3
−2 −3
Cevap A
4.
9.
=
A 0 ise rankA < 3 tür.
I, II, III öncüller doğrudur.
Cevap D
=
A
2 a −1
4=
0 2 0
1 1 0
⇒ A = 2. ( −2 ) − a ( −2 ) + ( −1)( 4 ) = 0
⇒ A =−4 + 2a − 4 =0
5.
Yalnız III
2a = 8
a=4
Cevap C
Cevap E
27
ÖABT Lineer Cebir
GENEL TARAMA SINAVI
10. B.Ek ( A ) = A −1
13.
2. denkle min 2 katını
a + 3b + 2c =
1
3. denkle min 5 katını alıp
2 2a + b − c =−3
3 denklemi de taraf tarafa
3a − b =
9
5
toplarsak;
B Ek ( A ) .A = A −1.A
B A = Ι
B =
1
1
1
⇒ B = 2 ⇒ B =
A
4
2
a + 3b + 2c =
1
4a + 2b − 2c =
−6
15a
5b
45
−
=
+
20a = 40 ⇒ a = 2
3.2 − b =
9
b = −3
2.2 − 3 − c =−3
4 − 3 − c =−3
1 − c =−3
c=4
Cevap E
a.b.c =
2. ( −3 ) .4 =
−24
2
11. A − A =
Ι
Cevap A
A (A − Ι) = Ι
A . A −Ι =
Ι
3 A − Ι =1
A −Ι =
1
3
14. I, II, III
Cevap B
Cevap E
15.
A ≠ 0 ve regüler (tersi var)
I, II
12.
A = 0 olmalı ki aşikar olmayan çözümleri
Cevap C
olsun,
1 1 1
=
A 2=
1 3 0
1 0 a
A = (1.1.a + 2.0.1+ 1.1.3 ) − (1.1.1+ 3.0.1+ a.1.2 ) = 0
A =
( a + 0 + 3 ) − (1 + 0 + 2a ) =
0
16.
A = a + 3 − 1 − 2a = 0
( , +, )
cisim değildir.
Dolayısıyla
2=a
( , +, ) , ( , +, )
üzerinde vektör
uzayı değildir.
Cevap E
Cevap E
28
ÖABT Lineer Cebir
GENEL TARAMA SINAVI
17. I, II, III öncül alt vektör uzay şartlarıdır.
21. B seçeneğindeki vektörler birbirinin skaar katı
olduğu için lineer bağımlıdır. Taban (baz) teşkil
Cevap E
etmez.
C seçeneğindeki vektörlerde birbirinin skalar
katı olduğu lineer bağımlıdır. Taban (baz) teşkil
18. Verilen öncüllerin hepsi lineer bağımlılık için
etmez.
doğrudur.
E seçeneğinde ise (0, 0) bulunduğu için lineer
Cevap E
bağımlıdır.
D seçeneği ise,
(1,2=)
a ( 0,1) + b ( −1,0 )
Şeklinde lineer kombinasyonu olarak yazılabil-
19. I) V yi geren her küme en az n tane vektörü
diği için lineer bağımlıdır.
kapsar.
A seçeneği lineer bağımsız vektörlerden oluştu-
II) V deki lineer bağımsız küme en fazla n tane
ğu için 2 uzayı için bir baz (taban) teşkil eder.
vektörü kapsar.
I ve II öncüllerin doğruları yukarıdaki ifadeler
Cevap A
olmalıydı.
Sadece III öncül doğrudur.
Cevap C
22. Ter simetrik matris A T = − A dır.
20. i) 04 ∈ U
AT =
A olduğundan A =
( −1)3
A
ii) u1 + u2 ∈ U
A =
− A ⇒2A =
0
iii) a.u ∈ U
A = 0 tekil matristir.
rankA < 3 tür.
I) ( 2,0,0 ) , ( 0,3,0 ) , ( 0,0, 4 ) için
Cevap E
i) sağlanır
ii) ( 2,3,4 ) gelir bu şart sağlanmaz.
{( x, y,z ) x.y.z = 0} 3 ün alt vektör uzayı değildir.
II) i) (0, 0, 0) sağlanır.
ii) (2, 0, 0), (0, 3, 0), (0, 0, 4)
(2, 3, 4) sağlanır.
1 0
0 1
5 1
5 2
23.
1 → r2
1 ↔ r1 + 5r2
2 → 3r2
r
r
r
0
1
1
0
1
0
3 0
iii) -4(2, 3, 4) sağlamaz x ≥ 0 değil
{( x, y, z ) x ≥ 0} 3
ün alt vektör uzayıdır.
Cevap C
Cevap B
29
ÖABT Lineer Cebir
GENEL TARAMA SINAVI
24. A seçeneğinde 3 satırda 2 satırdaki 1. Den
29. II, III
önce gelmiş satır (eşelon) değildir.
Cevap D
C seçeneğinde sıfır satırlar en altta yer almalıydı satır (eşelon) değildir.
D ve E seçeneğinde 1 in bulunduğu diğer sütunlar sıfır olmalıydı satır eşelon değildir.
30. I, II, III
Cevap B
Cevap E
31. x + 2y =
0
x=
−2y
2x − z = 0 ⇒
y = k olsun
x = −2k
z = −4k
25. T : u → V
lineer dönüşüm olması için,
I ve III öncüllerin sağlanması gerekir.
2x = z
k [1 −2 −4]
Cevap C
Cevap B
32. A
=
26. I. ve II. öncül doğrudur.
3 − λ −1
= 0
−3 5 − λ
( 3 − λ )( 5 − λ ) − 3 = 0
Cevap D
15 − 3λ − 5λ + λ 2 − 3 = 0
λ 2 − 8λ + 12 = 0
λ
−6
λ
−2
2
λ=
λ=
1 6
2
( A − λΙ ) x = 0
1) x 2 0
( 3 − λ ) x1 + ( −=
−3x1 + ( 5
=
− λ ) x2 0
27. I, II, III
Cevap E
=
λ1 6 için
( −3=
) x1 − x2
0
0
−3x1 − x 2 =
3x1 = − x 2
x1 = t olsun
1 1
28. T =
0 −1
T
−1
T
−1
1
x2 =
−3t ⇒ t
−3
2 için
λ2 =
−1 −1
= −1
0 1
x1 − x 2 0
=
1 1
=
0 −1
x1 x 2
=
−3x1 + 3x 2= 0
1
k
1
Cevap A
30
x1= k, x 2= k
ÖABT Lineer Cebir
GENEL TARAMA SINAVI
2−λ
1
1
=
P1 =
ve P2 vektörleri lineer bağım −3
1
35. A
=
3
5
sız ve 2 tane olduğundan A köşegenleştirilebilir.
0
1
3−λ
( 2 − λ )( 2 − λ )( 3 − λ ) − 2 = 0
( 4 − 2λ − 2λ + λ2 ) (3 − λ ) − 2 =0
1 1
3 1
−
1
1
−
1
P−1 =
4 3 1
1 1 −1 3 −1 1 1
P−1 A .P =
4 3 1 −3 5 −3 1
1 6 −6 1 1
=
4 6 2 −3 1
P
=
0
2 − λ=
2
0
[P=
1 P2 ]
( 4 − 4λ + λ ) ( 3 − λ ) − 2 = 0
2
12 − 4λ − 12λ + 4λ 2 + 3λ 2 − λ3 − 2 =0
−λ3 + 7λ 2 − 16λ + 10 =0
( λ − 1) ( λ2 + 6λ − 10 ) =0
=
λ 1, λ 2 + λ=
6
3
1 24 0
=
4 0 8
6 0
=
0 2
λ1 + λ 2 + λ3 = 7
Cevap C
Cevap C
33. I, II, III
Cevap E
36.
A =0
2 −1
=
A
−3
1
−1 − 1 =
4
0
−2 3 − 1
1 1 −3
A =
a −2 4 =
0
1 −2 2
4 −3 5 0 −5 −1 0 0 9
34. T = 0 1 2 0 1 2 0 1 2
2 1 3 2 1 3 2 1 3
0 0
0 1
2 1
rankT
a
1
A = 1( −4 + 8 ) − 1( 2a − 4 ) − 3 ( −2a + 2 ) = 0
A = 4 − 1( 2a − 4 ) − 3 ( −2a + 2 ) = 0
A = 4 − 2a + 4 + 6a − 6 = 0
1 0 0 1 0 0 1
2 0 1 0 0 1 0
3 2 1 0 2 0 0
=3
4a = −2
1
a= −
2
Cevap A
Cevap D
31
ÖABT Lineer Cebir
37.
GENEL TARAMA SINAVI
( A − λΙ ) x = 0
A
=
A=
A=
41. I ve II öncül daima alt vektör uzay olur.
III öncül için kesinlik yoktur.
2−λ
4
= 0
1
−1 − λ
( 2 − λ )( −1 − λ ) − 4=
Cevap C
0
( −2 − 2λ + λ + λ ) − 4 =
2
A = λ2 − λ − 6 = 0
λ
−3
λ
0
λ1 =3, λ 2 =−2
42. Verilen seçeneklerde D seçeneğinde 2 satır
+2
x1 + 4x 2
( 2 − λ )=
x1 + ( −1 − λ ) x 2 =
0
işlemi olduğundan elementer matris değildir.
=
λ1 3 için
Cevap D
0 −1x1 + 4x 2 = 0
x1 − 4x 2 =
0
λ 2 =−2 için
x1 =4x 2
4x1 + 4x 2 = 0
x2 = t
x1 + x 2 =
0
4
t
1
x1 = − x 2
x1 = 4t
1
−1
k yada k
−
1
1
Cevap A
38. I, II, III
Cevap E
39. Verilen öncüller teoremdir.
Cevap E
40. Verilen öncüllerin her biri doğrudur.
Cevap E
32