LYS1 / 6.DENEME
MATEMATİK TESTİ ÇÖZÜMLERİ
1.
5.
27
6
1
+
= 3, 18
9
30
50
Cevap: C
2. ve 3. denklem taraf tarafa toplanırsa
z=4
x + y – 8 = 12
x + y = 20
–x + 3y – 24 = 4
–x + 3y = 28
y = 12
2.
2
x −8 = 1
2
x − 8 =− 1
2
x −m = 0
x =9
x =! 3
2
x =7
x =! 7
2
x =m
Cevap: B
2
(–9) . (–7) . (–m) = (–189)
m=3
Cevap: E
HARF EĞİTİM YAYINCILIĞI
4 ` x2 - 9 j + 16 ` x2 - 9 j = 42
3.
6.
a < 0 ve b > 0
−a + a + b − b
−a + a + b − b = 0
Cevap: C
6 x2 - 9 = 42
x2 - 9 = 7
x2 - 9 = 49
x2 = 58 $ x = ! 58
çarpımı -58
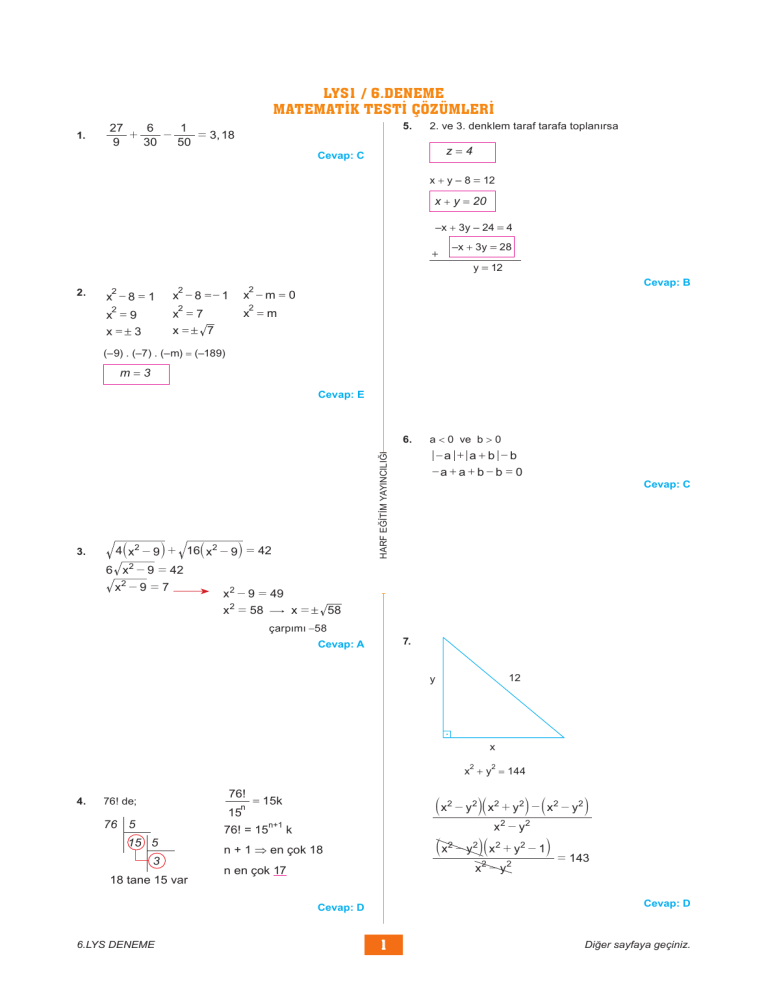
7.
Cevap: A
12
y
x
x2 + y2 = 144
4.
76! de; 76 5
15 5
3
18 tane 15 var
6.LYS DENEME
76!
n
15
a x2 - y2 ka x2 + y2 k - a x2 - y2 k
= 15k
76! = 15n+1 k
x2 - y2
n + 1 ⇒ en çok 18
a x2 - y2 ka x2 + y2 - 1 k
n en çok 17
x2 - y2
Cevap: D
1
= 143
Cevap: D
Diğer sayfaya geçiniz.
8.
112 + 52 . 112 = 112 . (1 + 52) = 112 . 26
12. 11x + 7 = 3(3x + 5) + (2x – 8)
2
3x + 5 = 1(2x – 8) + (x + 13)
13
2x – 8 = 2(x + 13) – 34
EBOB 34’ün 1’den farklı böleni olmalıdır.
EBOB (11x + 7, 3x + 5) = EBOB(x + 13, 34) ∈ {2, 17, 34}
x + 13 = 2k
x + 13 = 17m
x + 13 = 34n
x = 2k – 13
x = 17m – 13
x = 34n – 13
{Tüm tek sayılar}
{xmax = 72}
= 11 . 2 . 13
en büyük asal çarpan
Cevap: D
9.
Para = 6x + 4 = 8y + 2
Para + 14 = 6x + 18 = 8y + 16
Para + 14 = 6(x + 3) = 8(y + 2)
Para + 14 = okek (6, 8)
Para + 14 = 24k (k = 20)
Para = 466
13. (mod 17)x ≡ 15+25+35+45+ … +85+95+…+145+155+165
Cevap: B
10. 36 ile tam bölündüğüne göre 4 ve 9 ile tam bölünebilmektedir.
AA2500
AA2544
AA2588
11
66
22
bb
^6, 4h `b
b 3 farklı sayı yazılır.
^2, 8h bb
a
(mod 17)x ≡ 15+25+35+ … +(–3)5+(–2)5+(–1)5
(mod 17)x ≡ 0
HARF EĞİTİM YAYINCILIĞI
^1, 0h _bb
Cevap: D
14.
Cevap: A
7a / b `mod 10 j
7 / 7 `mod 10 j
7 2 / 9 `mod 10 j
3
7 / 3 `mod 10 j
4
7 / 1 `mod 10 j
7
Cevap: ÜÇ
7
7
7i
/ a `mod 4 j
7 / 3 `mod 4 j
1
2
7 / 1 `mod 4 j
3
7 / 3 `mod 4 j
11.
4
7 / 1 `mod 4 j
a = 3 ( 7 / 3 `mod 10 j
3
–63 5
–65 –13
2
Cevap: B
x = − 13
4 x + y = –11
y=2
Cevap: D
15. Devre incelendiğinde akıma geçen yer, sadece r ve r'
nün olduğu yerdir. Dolayısıyla Z ve T
6.LYS DENEME
2
Cevap: E
Diğer sayfaya geçiniz.
16. 2. adımda ve 3. adımda hata yapılmıştır.
7 6 5
I. f p $ f p $ f p = 210 tane
1 1 1
21.
Cevap: B
II. 5 " 5
6"6
7 " 7, 8, 9, 10, 11
14444444244444443
5
6"9
7 " 10, 11
\
Lise
Lisans
Tecrübeli
y erkek
x kadın
x erkek
y kadın
z
z + 36
Tecrübesiz
2z + 36 = 2(x + y) ⇒ x + y = z + 18
3
1
5"6
6"7
7 " 8, 9, 10, 11
1444442444443
4
6"8
7"
14444244443
3
6"9
7"
144424443
1
h
Cevap: C
5.6 4.5 3.4 2.3 1.2
+
+
+
+
= 35 tane artan fonksiyon
2
2
2
2
2
III.Aynı mantıkla 35 tane de azalan fonksiyon vardır.
4
2
1
1
2
2
İkinci sıra seçiminde ise, e o $ e o $ 3! şeklinde işlem
yapılır. Bu durumlar bağlantılı olduğu için de bulunan
sonuçlar çarpılıp cevap bulunur.
Cevap: B
23. (+) toplama işaretini ayraç olarak alırsak,
I, II, III kesinlikle çift fonksiyondur.
2
1
göre ilk sıranın seçimi; e o $ e o $ 3! şeklinde bulunur.
HARF EĞİTİM YAYINCILIĞI
Cevap: C
19. f(x) = f(-x) olursa çift fonksiyondur.
Cevap: E
22. Her satıra bir tek sayı gelmek zorunda bu dağılıma
]Z] x - 2
]]
, x15
-1
18. f _ x i = [] 3
olur.
]]
] x - 4, x $ 5
\
2
6 " 10
7 " 11
T
x + y – z = 18
4
6"8
7 " 9, 10, 11
14444244443
6 " 10
7 " 11
T
2
17.
6"7
7 " 8, 9, 10, 11
1444442444443
Cevap: C
+ rakam
f
11
11.10.9
p=
= 165
3
3.2
Cevap: D
20. (f–1og)(0) = 5
(f–1og)(2) = 4
→
–1
(f og)(7) = 0 (fof–1og)(7) = f(0)
g(2) = f(4)
g(7) = f(0)
–1
–1
–1
6.LYS DENEME
Tura
Yazı
Yazı
Tura
Tura
Gelen yüz tura olduğuna göre yazı - yazı olan para
seçersek geriye 3 tane yüz kalır. 2’si Tura olduğuna
7 = g (f(0))
7 + g(2) – f(4) =
Yazı
gelemez. Geriye kalan paralardan Tura olan bir yüzü
(g og)(7) = g (f(0))
24.
(fof–1og)(2) = f(4)
göre cevap
7
Cevap: A
3
2
’tür.
3
Cevap: B
Diğer sayfaya geçiniz.
4x 2 - 36xy - 9y 2
0
= 2
y2
y
25.
28. a = –1 için
2
x
x
4. f p - 36. f p - 9 = 0
y
y
f p nin alabileceği değerler toplamı $
x
y
- b 36
=
=9
a
4
b=2
1
için a + 1 + b – 2 = 0
a=
2
b değerleri toplamı 2 +
a+b=1
b=
Cevap: B
1
2
1
5
=
2
2
y
26.
29. P(x) = a(x + 1)(x – 2)(x – 3)(x – 4) + 17
f(x) = ax2 + b
x = 0 ⇒ y = –10 b = –10
x
f(x) = ax2 – 10
y = –6
4 br
2
f(x) = –4x – 10
27.
a=3
P(x) = 3(x + 1)(x – 2)(x – 3)(x – 4) + 17
P(0) = 3 . 1 . (–2) . (–3) . (–4) + 17 = –31
f(–5) = –10
Cevap: D
HARF EĞİTİM YAYINCILIĞI
89 = a . 4 . 3 . 2 . 1 + 17
4a – 10 = –2b
a = –4
T.N (0,–10)
Cevap: A
30. P(–1) = 4
P(2) = 7
P(x) = (x – 2) (x + 1) Q(x) + (ax + b)
− 1 # x # 0 ( g ]x g $ f ]x g $ 0
x#0
x . f ]x g # 0
g ]x g $ x . f ]x g
"− 1, 0 ,
−a + b = 4 a = 1
3
2a + b = 7 b = 5
0 < x < 5 ( 0 < g ]x g < f ]x g
f ]x g . x > g ]x g
Q
x $ 5 & g ]x g # 0 < f ]x g
f ]x g . x > g ]x g
Cevap: C
31.
D
C
E
180 – 2α
α
A
Q
Cevap: E
Cevap: B
tan α =
α
B
5
12
12
13
5
sin ]180 - 2ag = sin 2a = 2 sin a cos a
5 12
120
=2$
=
$
13 13
169
6.LYS DENEME
4
Cevap: E
Diğer sayfaya geçiniz.
32. 4tanx = 1 – tan2x
35. 2a = 15
tan2x + 4tan x –1 = 0
(tanx + 2)2 – 5 = 0
(tan x + 2)2 = 5
tan x = 5 - 2
a = 1 + ^ 5 - 2h
2
x
a
1
5 -2
3<a<4
b
0 < b < 1
3 =7
1<c<2
10 = 5
c
a>c>b
Cevap: C
2
2
a = 1+ 9 - 4 5
a = 10 - 4 5
sin 2x = 2 sin x + cos x
5-2
1
= 2.
$
10 - 4 5
10 - 4 5
2. 5 - 2
1
=
=
10 - 4 5
5
10 a + a + 9r
5
a 1
k = aa1 + a1 + 4r k + 120
1
2
2
10a1 + 45r = 5a1 + 10r + 120
5a1 + 35r = 120
36.
a1 + 7r = 24 → a1 + 7r = a8 olduğundan cevap 24
Cevap: B
Cevap: B
2
HARF EĞİTİM YAYINCILIĞI
33. cos2x + sin2x = 1
cos 4x + sin4x + 2sin2x . cos2x = 1
2
5
+ 2 $ _sin x. cos x i = 1
8
2
sin 2x
3
=
4
8
3
2
sin 2x =
4
3
sin 2x =
2
2$
30, 75, 210, 255
sin 2x = -
105, 295, 150, 330
3
2
3
4
4
2
4
+
+f p +f p + g
9
9
3
9
37.
4
9
n
3
4
2
2
f p =
+
+
3 n=1 9
3
/
4
19
=
38.
Cevap: A
2
4
22
+
=
3
5
15
Cevap: A
7
7 - 3 - 5- 3 + 3
0
3
7 - 5- + 3
1
1- 3 +3 = 4
5
Cevap: E
34. a. log3 x = 2b log 2 x
log2 x
a
=
2b
log3 x
39.
a
= log2 x . log x 3
2b
a
a
= log2 3 $
= 2 log2 3
b
2b
= log2 9
6.LYS DENEME
3
lim
x"3
x+1
1 + 2x
2
2x
- 2 .2
2x
5
2x + 3
+3
+5
-3 + x
4-x
1-x
-5
=
3
3
belirsizliğinde en yüksek dereceli terimlerin katsayıları
oranı limiti verir.
Cevap: B
-2
2 .2
3
= -4
Cevap: B
Diğer sayfaya geçiniz.
40.
Y0
x2 + ax + 1 =
D10
a2 - 4 1 0
44.
1
2
–2
-
+
(–2, 2)
+
x
Cevap: C
O
A = 2x . y = ?
2
2
x +y =1
y = 1-x
2
y
x
A = 2x. 1 - x2
A' = 2. 1 - x2 + 2x.
4 - 4x 2 - 4 x 2 = 0
8x 2 = 4
1
2
1
$
x2 =
1
2
y=
2
x=
41. Önce limitine ve sürekliliğine bakalım.
lim f _ x i = lim f _ x i = f _- 1 i
x "- 1
x "- 1
2 1 - x2
=0
b_b
bb
bb
b`b A = 1
bb
bb
a
+
–1 = b + a = –d
Cevap: C
`- 1+ j = `- 1- j olmalı.
'
'
–a = 3
a =- 3
-
b=2
d = 1 olduğuna göre,
b + d = a işleminin sonucu 6 dır.
Cevap: D
HARF EĞİTİM YAYINCILIĞI
_- 2x i
45. x > 0
g(x) > 0
f(x) > 0
g'(x) < 0
f'(x) > 0
Şıkların tek tek türevleri alındığında doğru cevabın A
şıkkı olduğu görülür.
2 sin x cos x
x cos x
dx = #
dx
# 1 2+sin
2 cos x - 1
1 + 2 cos x - 1
46.
2
42. (fof)(0) = sayı olduğundan sayının türevi 0 dır.
Cevap: A
2
#
= #
=
Cevap: D
cos x = u
- sin x.dx = du
sin x
dx
cos x
- du
= - ln u + c
u
= - ln cos x + c
1
= ln
+c
cos x
= ln sec x + c
43.
f_x i =
Cevap: C
sin 2x
2
1. türev = cos2x
2. türev = –sin2x
Her 4 sayıda aynı ifade
geleceğinden
47. x 2f(x) = 5x4 + 8x3 + 9x 2
2
3. türev = –2 cos2x
Cevap: - 234 cos 2x
f(x) = 5x 2 + 8x + 9
mT = f'(x) = 10x + 8
3
4. türev = 2 cos2x
4
5. türev = 2 cos2x
f'(-2) = –20 + 8 = –12
6.LYS DENEME
Cevap: A
Cevap: D
6
Diğer sayfaya geçiniz.
48.
_b
bb
t = arc sin x
bb
bb
x = sin t
bb
bb
dx = cos t dt
b
-1
r `bb
x=
için t =
b
4 bb
2
bb
bb
r
bb
x = 1 için t =
2
b
a
52. E noktası BGC nin ağırlık merkezidir.
r
2
sin t . cos t . dt
#
1 - sin 2 t
r
4
r
2
=
# sin t . dt
|AD| = 72 = 9m ⇒ m = 8
|DE| = 8
r
4
Cevap: D
Cevap: C
53.
#
1
f
'
f '_ x i f _ x i
f_x i
p $ dx
- 2 p $ dx = f
x
x
x
1
4
f_x i
=
x
50.
#
4
1
2m
f _ 4 i f _1 i 12 2
=
=
- = 1
4
1
4 1
Cevap: B
E
m
60°
60°
a
b_b
b
f _ x i dx = S1 - S2 bbb
bb S + S - S - S = 34 - 16
-8
b 1
3
2
4
`b
4
bb
= 18
g ` y j dy = S3 - S 4 bbb
bb
b
-4
a
AD
=2
DC
D
4a
60°
HARF EĞİTİM YAYINCILIĞI
4
49.
A
2a
30°
B
C
Cevap: E
8
#
54.
#
2α
α
Cevap: ONSEKİZ
olduğundan
A
E
70°
70°
51. ABC ikizkenar üçgen olduğundan γ > β = θ > α
B
40°
D
C
Cevap: B
6.LYS DENEME
20°
7
Cevap: A
Diğer sayfaya geçiniz.
55.
I.
57.
A
D
C
A
A
G noktası ağırlık merkezi olduğundan;
G
K
F
A
8
C
B
A
II.
A
Alan (ABC) = 3A
A
B
k
D
E
B
Taralı dörtgen paralelkenardır.
T.A. = 6.8. sin 150 = 24
A(ABCD) = 48 br 2
C
E
6
150°
Cevap: E
3k
A
O halde;
D S
58.
A = 28 + K
A = S + K + 16
S = 12 br2
K
A
x
E
K
E
G
16
K
C
y
Cevap: D
P
y
L
Ç(ABCD) = 2x + 2y + 2a + 2b = 34 br
Cevap: A
A
24 E
α
α
B
3x
4
m
α+β
a
3 y
m
12
2p
2b
C
12
p
2m
3m
C
K noktası ABD üçgeninin,
L noktası BDK üçgeninin, ağırlık merkezidir.
A _EKLFD i = 18 br2
Cevap: D
6.LYS DENEME
F
b
&
&
ABF ile CBD benzerdir.
3m y
=
4m x
3x
y=
4
3x
e 32 gelirse, 3x'e 128 gelir.
4
b
6
B
a
D
L
x
β
E
x
6
6
D
8
2y 3
6
2x
y
C
a+b=8
2x
β
a
2a
y
b
x+y=9
F
A
x
F
59.
56.
D
a
b
B
HARF EĞİTİM YAYINCILIĞI
B
a
x
b
28
F
y
8
Cevap: A
Diğer sayfaya geçiniz.
60.
63.
D
D
x
β
b
E
A
β
72°
F
α
36°
C
72° 72°
x
β
B
36°
x
α
A
C
E
&
a
8
_ ADE i de ÖKLİD uyglarsak;
=
27 b
a2 = 8 . b
a . b = 27 . 8
2
a
a3 = 27.2b
b=
8
a = 12
x=3
Ç(ABFE) = 12
Cevap: D
B
2
y + x. y = 9
&
&
EDC ile CFD benzerdir.
x+y x
=
x
y
2
x = xy + y2
b = 18
AD = 6 5
x
8
8
36°
27
x
72° 36°
61.
D
C
HARF EĞİTİM YAYINCILIĞI
x
68
E
8
α
A
2
α
β
B
68
Taralı üçgende kosinüs teoreminden;
Cevap: B
x2 = 68 + 64 $ 2 $ 8 $ 68 $
2
68
x = 10
Cevap: E
62.
E
2
2
1
F
D
C
64.
2
2
K
45° 45° 1
45° 45°
45°
45°
1
A
B
G
J
6.LYS DENEME
13
A
H
B
2
2
EK =
+
+1 = 2+1
2
2
y
Cevap: A
9
1 C
12
O
12
D
x
Cevap: A
Diğer sayfaya geçiniz.
65.
B
67.
30
D
E
8
K
8
C
30
8
8
30°
O
8
8
30°
8
D
4 3
F
120°
4
L
30
4
30°
30°
4
F
8
A
4 3 − 4
A
2
4 f r.8 .
4 3
4 3 − 4
B
120
256r
- 16 3 p =
- 64 3
360
3
4
4
E
Cevap: A
4
4 3 − 4
68. y = 0 için x = –4
Pisagordan;
2
2
a 4 3 + 4 k + a 4 3 - 4 k = 48 + 16 + 32 3 + 48 + 16 - 32 3
= 128
` EF + FD j = 128
2
=8 2
Cevap: B
HARF EĞİTİM YAYINCILIĞI
(–4, 0)
2x – y + 8 = 0
m=2
Bu doğru ile dik kesişen doğrunun eğimi -
O halde denklem,
1
y - 0 = - `x + 4j
2
2y = - x - 4
2y + x + 4 = 0
Cevap: B
69.
d2
y
d1
66.
D
C
45°
5
y
A
3
4 2
B
8
45°
A
O 4
E
A
1
2
8
A
A
B
45°
45°
8
B
6.LYS DENEME
x
8
d1 ve d2 doğruları ortak çözülürse;
3/ 5x + 8y = 40
- 5/ 3x + 4y = 12
4y = 60
Taralı Alan =
4.15
= 30
2
y = 15
4 2+4 2
= 16
A+B =
2
4
Cevap: B
10
Cevap: C
Diğer sayfaya geçiniz.
70. 2x – 3y + 4 = 0
74.
(x, y) sağlasın.
(x, y)
2x – 3(4 – y) + 4 = 0
2x – 12 + 3y + 4 = 0
D
(x, 4 – y)
2x - 3y - 8 = 0
`a + 1 j x - 3y + c = 0
C
14
25
T
25
14
A
T'
B
2si de aynı doğru olduğundan
c=8
a =- 3
h = 24 olur.
2
V = 14 . 24 = 1568
3
25
Cevap: C
7
7
7
Cevap: B
71. y = x doğrusu üzerinde keyfi bir nokta seçelim.
(1, 1) olsun.
x =
`3, 5 j`1, 1 j
2
8
=
=4 2
2
Cevap: E
HARF EĞİTİM YAYINCILIĞI
75. Vsilindir = πr 2h
Alan = 2πr 2 + 2πrh
πr 2h = 2πr 2+ 2πrh
rh = 2r + 2h
rh – 2h = 2r
h(r – 2) = 2r
2r
h=
r-2
AD = 2 5 Taralı üçgende kosinüs teoreminden;
AD = 4 5 D'C = 68
68 = 80 + 20 - 2. 2 2 .4 5 = cos Q
68 = 100 - 80. cos Q
32 2
=
cos Q =
80 5
AC . AD' = AC . AD' . cos Q
2
= 4 5 $ 2 5 $ = 16
5
72.
Cevap: E
76.
A'
E
Cevap: D
4
6
6
B'
2
D
B
x = 216
73. Şıklardan doğru cevabın D olduğu görülür.
6.LYS DENEME
2
11
C
Taralı bölgenin hacmi =
2.6
$ 6 = 36
2
x=6
Cevap: D
C'
6
F
A
D'
6
2
Cevap: E
Diğer sayfaya geçiniz.
77. Üç dikme teoreminden
79.
[BD] ⊥ [DC]
A
M1
45°
B
4
2 2
D
45°
4 45° 2 2
E
C
M2
M1(a, –2)
M2(–4, 3)
r1 = 34 r2 = 27
M1 M2 = 61
`a + 4 j + `- 2 - 3 j = 61
2
Cevap: A
2
2
a + 8a + 16 + 25 = 61
2
a + 8a - 20 = 0
a nın alabileceği değerler toplamı - 8
HARF EĞİTİM YAYINCILIĞI
78. (x – 1)2 + (y + 1)2 = 4
80. a2 = 25
a = 5
b2 = 21
m(1, –1)
(1, –1) noktasının 3x – 4y + 13 = 0 doğrusuna
3 + 4 + 13
olan uzaklığı
=4
5
Cevap: A
r=2
a2 = b2 + c2
2
25 = 21 + c c = 2
|FF'| = 4
|PF| + |PF'| = 2a
yani 10
Çevresi = 14
Cevap: ONDÖRT
2
2
6.LYS DENEME
Cevap: A
12
Diğer sayfaya geçiniz.










