2. - Google Groups

ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
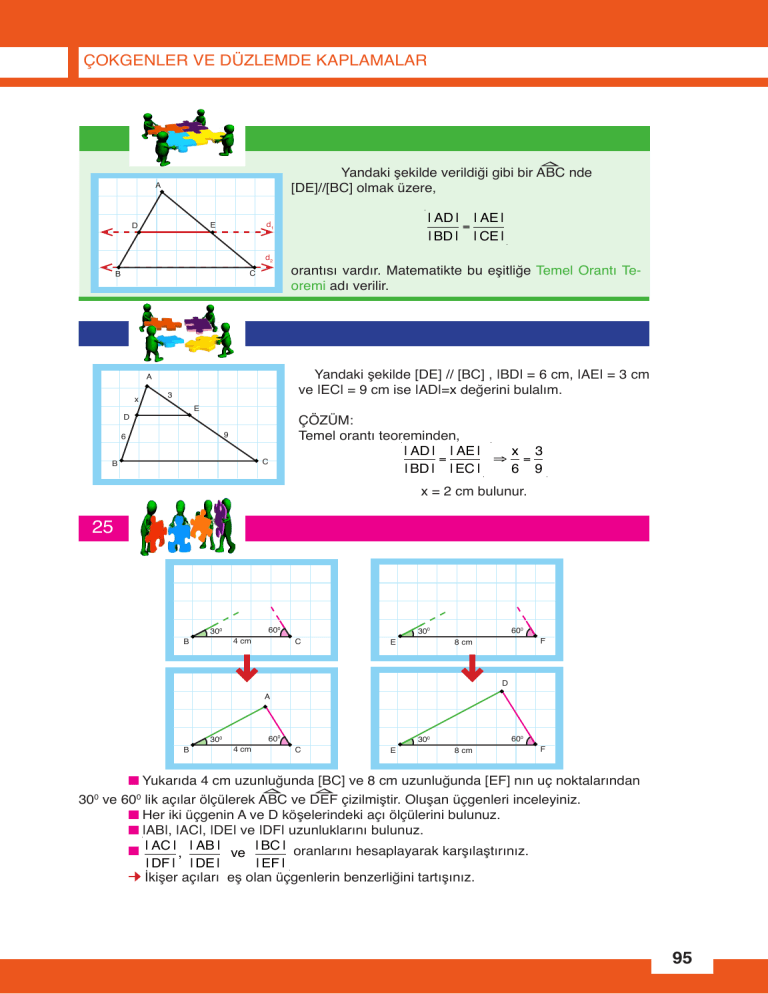
Yandaki şekilde verildiği gibi bir ABC nde
[DE]//[BC] olmak üzere,
A
d2
C
B
orantısı vardır. Matematikte bu eşitliğe Temel Orantı Teoremi adı verilir.
Yandaki şekilde [DE] // [BC] , |BD| = 6 cm, |AE| = 3 cm
ve |EC| = 9 cm ise |AD|=x değerini bulalım.
A
x
| AD | | AE |
=
| BD | | CE |
d1
E
D
3
E
D
9
6
C
B
ÇÖZÜM:
Temel orantı teoreminden,
| AD | | AE |
x 3
=
⇒ =
| BD | | EC |
6 9
x = 2 cm bulunur.
25
B
300
4 cm
600
C
E
300
600
8 cm
F
D
A
B
300
4 cm
600
C
E
300
8 cm
600
F
Yukarıda 4 cm uzunluğunda [BC] ve 8 cm uzunluğunda [EF] nın uç noktalarından
300 ve 600 lik açılar ölçülerek ABC ve DEF çizilmiştir. Oluşan üçgenleri inceleyiniz.
Her iki üçgenin A ve D köşelerindeki açı ölçülerini bulunuz.
|AB|, |AC|, |DE| ve |DF| uzunluklarını bulunuz.
| AC | | AB |
| BC | oranlarını hesaplayarak karşılaştırınız.
,
ve
| DF | | DE |
| EF |
İkişer açıları eş olan üçgenlerin benzerliğini tartışınız.
95
2. ÜNİTE
D
α
A
α
β
β
E
C
B
F
Yukarıdaki ABC ve DEF
lerinde olduğu gibi karşılıklı iki
açısı birbirine eşit olan üçgenler benzerdir. Bu benzerliğe Açı
Açı (A.A.) benzerlik aksiyomu
denir.
.
A
B
C
E
ÇÖZÜM:
[AB]//[DC] ⇒ m(ABC) = m(DCE)
[AC]//[DE] ⇒ m(ACB) = m(DEC)
(Yöndeş açılar)
(Yöndeş açılar)
Dolayısıyla A(ABC) A(DEC)
(Açı açı benzerliği)
O hâlde,
| AB | | AC |
x
2
=
⇒
=
⇒ x = 2,4m bulunur.
| DC | | DE |
1,8 1,5
E
A
12
B
96
Yandaki resimde görülen çatı iskeletinde
[AB]//[DC],
[AC]//[DE],
|DE|=1,5m,
|AC|=2m ve |DC|=1,8m ise |AB| nun kaç
metre olduğunu bulalım.
D
x
13
C
24
D
Yandaki şekilde [AB] ⊥ [BC], [AC] ⊥ [CE] ve
[CD] ⊥ [DE] dir. B, C ve D doğrusal noktalar,
|AB|=12cm, |AC|=13 cm ve |CD|=24cm olduğuna
göre |CE|=x değerini bulalım.
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
E
A
α
m(ACB)= α ve m(ECD)= β olsun. C köşesinde
oluşan açıların ölçüleri toplamı ile üçgende iç açıların
ölçüleri toplamının eşitliğinden,
β
12
B
x
13
α
C
β
D
24
ÇÖZÜM :
m(BAC)= β ve m(CED)= α olur. Dolayısıyla,
ABC CDE (Açı Açı benzerlik teoremi) O hâlde,
| AB |
| CD |
=
| AC |
| CE |
⇒
12 13
=
⇒ x = 26 olur.
24 x
26
D
4 cm
A
6 cm
8 cm
3 cm
B
C
F
E
Çizilen ABC ve DEF dik üçgenlerini inceleyiniz.
Pisagor bağıntısı kullanarak bilinmeyen kenarları bulunuz. Bu üçgenleri aşağıdaki şekilde gösterildiği gibi A, D ile çakışacak biçimde dik açıları çakıştırarak üst üste
yerleştirelim.
A D
4 cm
A
4 cm
B
olur.
4 cm
3 cm
C
E
B
5 cm
10 cm
3 cm
C
3 cm
F
B ve C noktaları bulundukları kenarların orta noktaları olduğu için [BC], [EF] na paralel
m(B) ile m(E), m(C) ile m(F) ölçüsünü karşılaştırınız.
| AB | | AC |
| BC | oranlarını inceleyiniz ve orantı sabitini bulunuz.
,
ve
| DE | | DF |
| EF |
Karşılıklı ikişer kenar uzunluğu orantılı ve bu orantılı kenarların oluşturduğu açılarının
ölçüleri eşit olan üçgenlerin benzer olup olmadıklarını tartışınız.
97
2. ÜNİTE
D
A
k.c
c
α
E
C
a
B
α
k.a
F
Daha genel olarak
aşağıda gösterildiği gibi
karşılıklı iki kenar uzunluğu orantılı, bu kenarların
belirttiği açıları eş olan
üçgenler benzerdir. Bu
benzerliğe Kenar Açı Kenar (K. A.K.) benzerlik teoremi denir.
Yandaki resimde görülen elektirik direğinde m(ABC)=m(DEF) dir.
|AB|=2,4m, |BC|=3,2m, |AC|=5,2m, |DE|=3,6m ve |EF|=4,8m ise
[DF] bağlantı demirinin kaç metre olduğunu bulalım.
A
ÇÖZÜM:
| AB | | BC |
2,4 3,2 2
=
⇒
=
= ve m(ABC)=m(DEF) olduğundan
| DE | | EF |
3,6 4,8 3
B
ABC  DEF dir. (K. A. K. benzerliği).
O hâlde,
| AB | | BC | | AC |
2,4 3,2 5,2
=
=
⇒
=
=
⇒ x = 7,8m olur.
| DE | | EF | | DF |
3,6 4,8
x
C
D
E
F
27
A
B
H
D
C
E
K
98
F
Yandaki şekilde birim karelerden
oluşan zemin üzerine çizilmiş ABC ile
DEF ni inceleyiniz.
Pisagor bağıntısını kullanarak |AB|,
|AC|, |DE| ve |DF| nu, birim kareleri
sayarak |BC| ve |EF| nu bulunuz.
Karşılıklı eş açıları bulunuz.
| AB | | AC |
| BC | oranlarını
,
ve
| DE | | DF |
| EF |
karşılaştırınız.
Karşılıklı üçer kenar uzunluğu orantılı
olan üçgenlerin benzer olup olmadıklarını tartışınız.
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
D
A
c
B
M
F
CE
F
k.a
Yandaki resimde görülen teknenin S ve M yelkenlerinin
kenar uzunlukları |AB|=15m, |BC|=8m, |DE|=18m ve
|EF|=9,6m dir. m(ABC)= m(DEF)=900 olduğuna göre
yelkenlerin belirttiği ABC ile DEF nin benzerliğini
sorgulayalım.
D
S
B
E
C
a
A
k.b
k.c
b
Aşağıdaki şekilde de
görüldüğü gibi karşılıklı
üç kenar uzunluğu orantılı
olan üçgenler benzerdir.
Bu benzerliğe Kenar Kenar
Kenar (K. K. K) benzerlik
teoremi denir.
ÇÖZÜM:
Her iki üçgende Pisagor bağıntısından |AC|=17m ve
|DF|=20,4m bulunur.
15
8
17
5
=
=
= olduğundan K.K.K. benzerlik teoremine göre ABC  DEF dir.
18 9,6 20,4 6
28
D
A
B
C
H
E
K
F
Yanda birbirine benzer olan
ABC ile DEF nde kenar uzunluklarını bulunuz.
ABC ile DEF nin benzerlik oranını
yazınız.
ABC nin ve DEF nin alanlarını
hesaplayınız.
Hesapladığınız alanların oranı ile
benzerlik oranını karşılaştırınız.
Bu kez farklı oranlarda birbirine
benzeyen üçgenler alarak benzer
işlemleri yaparak benzerlik oranı ile
alanlar oranını karşılaştırınız.
Yaptığınız çalışmaları gözden geçirerek benzer üçgenlerde benzerlik oranı ile alanlar
oranı arasında bir genelleme yapmaya çalışınız.
99
2. ÜNİTE
k ∈ R olmak üzere, ABC  DEF
için,
| AB | | AC | | BC |
=
=
= k ise
| DE | | DF | | EF |
D
A
A(ABC)
C
B
E
A(DEF)
F
Yanda verilen A(ABC) nde
A(ABC)=8cm2 dir. Verilen açı ve
uzunluk ölçülerine göre A(DEF)
kaç cm2 olduğunu bulalım.
D
A
5 cm
2 cm
C
B
E
F
ÇÖZÜM:
ABC  DEF (A. A.) ⇒
A(ABC)
= k2 = ( 2 )2
5
A(DEF)
= k2 olur.
⇒
| AC | 2
= = k (Benzerlik Oranı)
| DF | 5
8
A(DEF)
=
4
⇒ A(DEF) = 50 cm2 bulunur.
25
29
B
C
100
d1
d2
A
D
Yandaki şekilde görüldüğü gibi birbirine paralel k1, k2 ve
k3 doğruları ile bu doğruları sırasıyla A, B, C ve D, E, F
noktalarında kesen d1 ve d2 doğrularını inceleyiniz.
k1
A ile F noktalarını birleştiren [AF] nı çizelim.
k2
E
F
k3
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
d1
d2
A
D
G
B
Çizdiğimiz [AF] ile k2 doğrusunun kesim noktasına G
diyelim.
k1
k3
F
C
d1
d2
A
D
B
A
B
C
d1
D
E
d2
d3
F
Birbirine paralel en az üç doğru, verilen iki doğruyu
kestiğinde bu iki doğru üzerinde orantılı doğru parçaları
ayırır. Bu durum,
k1 // k2 // k3 ise | AB | = | DE |
| BC | | EF |
k2
F
Bu kez FEG ve FDA nde temel orantı teoremini
yazınız.
Bu iki orantıdan çıkarılabilecek sonucu tartışınız.
k1
E
C
Oluşan ABG ve ACF nde temel orantı teoremini yazınız.
k2
E
k3
biçiminde ifade edilir. Bu teoremi bulan kişi Thales (Tales)
olduğu için verilen kural 1. Tales Teoremi olarak isimlendirilmektedir.
Yandaki resim şövalesi üzerinde B ve C noktaları arasındaki çıta
kırılmıştır. Kırık çıta sağlam çıta ile değiştirilecektir. d1//d2//d3, |DE|=60cm,
|EF|=40cm ve |AB|=45cm olduğuna göre |BC| nun kaç cm olduğunu
bulalım.
ÇÖZÜM:
1. Tales teoreminden,
| AB | | DE |
45 60
=
⇒
=
⇒ x = 30cm olur.
| BC | | EF |
x 40
101
2. ÜNİTE
30
d2
d1
B
E
d2
d1
A
k1
E
B
A
F
C
k2
k1
C
F
1. Şekil
k2
2. Şekil
Yukarıdaki şekillerde A noktasında kesişen d1 ve d2 doğrularını kesen birbirine paralel
k1 ve k2 doğruları çizilmiştir. Oluşan şekilleri inceleyiniz.
Şekillerdeki eş açıları belirleyiniz.
Eş açılardan faydalanarak benzer üçgenleri yazınız.
Benzer üçgenler arasında benzerlik oranını yazınız.
Buradan kenar uzunlukları arasında bir orantı yazmaya çalışınız.
Kesişen iki doğruyu, paralel iki doğru kestiğinde oluşan üçgenlerin karşılıklı kenarları
orantılıdır. Bu durum,
d2
d1
B
E
A
k1
B
A
C
d2
d1
F
k2
E
C
k1
F
1. Şekil
2. Şekil
| AB | | AE | | BE |
=
=
| AC | | AF | | CF |
| AB | | AE | | BE |
=
=
| AC | | AF | | CF |
k2
biçiminde ifade edilir. Bu teoremi bulan kişi Thales (Tales) olduğu için 2. Tales Teoremi
olarak isimlendirilir.
102
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
Yandaki resimde 1,6m boyundaki Ömer’in gölgesi zemin
üzerinde 2m ölçülmektedir.
Aynı anda gölgesi 50m olan
Dikilitaş’ın boyunun kaç m
olduğunu bulalım.
ÇÖZÜM:
2. Tales teoreminden,
E
B
1,6 m
A
2m
D
48 m
C
C
F
A
E
G
L
K
k
F
ABC de 2. Tales teoreminden
K
2k
x
E
14
6
| CG |
| CD |
=
| CF |
| CB |
=
1
olur.
3
Dolayısıyla, |CG|=m için |GD|=2m dir. (m ∈ R)
y
G
Yandaki şekilde [AC]//[KF], [FG]//[BD] ve
[GL]//[CE] dır. 2|CF|=|FB|, |AK|=6cm, |GL|=14cm,
|KB|=x cm ve |CE|=y cm olduğuna göre
x+y toplamının kaç cm olduğunu bulalım.
2|CF|=|FB| ⇒ |CF|=k için |FB|=2k dır. (k ∈ R)
C
m
x = 40 m bulunur.
F
ÇÖZÜM:
D
B
A
2 1,6
| DC | | BC |
=
=
⇒
50 x
| DF | | EF |
x
L
2m
ABC de 2. Tales teoreminden,
| BK |
| BA |
=
| BF |
| BC |
⇒
x
2k
=
⇒ x = 12 cm olur.
x + 6 3k
CDE de 2. Tales teoreminden,
B
D
| DG |
| DC |
=
| GL |
| CE |
⇒
2m 14
=
⇒ y = 21cm dir.
3m y
Buradan x+y = 12+21 = 33 cm bulunur.
103
2. ÜNİTE
31
Yanda A dik olan ABC dik üçgeninde hipotenüse ait
[AH] yüksekliği verilmektedir.
A
c
B
α
b
h
p
k
H
β
a
C
A
B
α
α
β
c
b
h
p
k
H
a
β
C
a, b, c, h, p ve k gerçek sayılar olmak üzere oluşan
üçgenlerin kenar uzunlukları a, b, c, h, p ve k olarak verilsin.
m(ABH) = α ve m(ACH) = β olarak alalım.
α + β = 900 , m(BAH)= β ve m(CAH)= α olur.
Benzer üçgenleri bulunuz.
Benzerlik oranından;
c nin p ve a cinsinden,
b nin k ve a cinsinden,
h nin p ve k cinsinden değerlerini bulunuz.
ABC üçgensel bölgesinin alan bağıntılarını kullanarak a, b, c ve h arasında bir ilişki
kurunuz.
Genel olarak a, b, c, h, p ve k gerçek sayılar,
m(A) = 900 olmak üzere kenar uzunlukları yandaki şekilde
verilen dik üçgende,
b
c
h
c2 = p.a (Dik kenar bağıntısı)
b2 = k.a (Dik kenar bağıntısı)
B
p
k
h2 = p.k (Yükseklik bağıntısı)
H
C
a
b.c = a.h (Alan bağıntısı) dir.
Bu bağıntıları bulan kişi Euclide (Öklid) olduğu için Öklid Bağıntıları olarak isimlendirilir.
A
Yandaki ABC dik üçgeninde [BA] ⊥ [AC], [AH] ⊥ [BC],
|BH|=9cm ve |HC|=16cm ise |AH|=x, |AB|=y ve |AC|=z
uzunluklarını bulalım.
A
y
B
9 cm
x
H
z
16 cm
C
104
ÇÖZÜM:
Öklid yükseklik bağıntısından,
x2 = 9. 16 ise x = 12 cm
Öklid dik kenar bağıntılarından,
y2 = 9. (9 + 16)
ve z2 = 16. (16 + 9)
y = 15 cm
z = 20 cm
bulunur.
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
Yandaki şekilde [BA] ⊥ [AD], |AB|=|AC|=10cm ve
|BC|=16cm ise |DC|=x değerini bulalım.
A
10
10
B
D
ÇÖZÜM:
x
C
x
C
[AH] ⊥ [BC] çizelim.
|BH|=|HC|=8cm
(ABC ikizkenar üçgen)
|HD|=8-x
|AH|= 6cm
(Pisagor bağıntısı)
ABD üçgeninden
|AH|2=|BH|.|HD| ⇒ 62=8.(8-x) (Öklid bağıntısı)
7
⇒ x = cm bulunur.
2
A
10
10
B
H
D
3.
1.
x
D
C
6 cm
E
F
6m
4m
4m, x m ve 6m uzunluğundaki üç
ağaç yukarıdaki şekildeki gibi iplerle
bağlanabiliyorsa ortadaki ağacın boyu kaç m
olabilir?
2.
A
x
D
3 cm
10 cm
A
xm
[DC] // [EF] // [AB], | DE | = 1 , |EF|=6cm,
| DA | 3
|AB|=10cm olduğuna göre |DC| = x kaç cm
dir?
4.
A
E
4 cm
B
6 cm
12 cm
y
B
12 cm
F
C
D
ABC ve ADE nde m(ADE) =m(ACB),
|AD|=x cm, |DB|=y cm, |BC|=12 cm,
|EC|=15cm, |AE|=3cm, |DE|=4cm olduğuna
göre x-y farkı kaç cm dir?
B
3 cm
E
x
C
ABC nde [DF] // [BE] ve [DE] // [BC], |AF|=6cm,
|FE|=3cm olduğuna göre |EC|=x kaç cm dir?
105
2. ÜNİTE
5.
4 cm
10.
A
A
D
6 cm
8 cm
B
B
E
2 cm
C
x
ABC nde |AD|=4cm, |DE|=5cm, |EA|=6cm,
|DB|=14cm, |EC|=4cm olduğuna göre
|BC|=x cm dir?
6.
A
4 cm
| AD | 4
= ,
| DB | 5
A(ADE)=16cm2 olduğuna göre BCED dörtgeninin alanı kaç cm2 dir?
11.
ABC nde [DE] // [BC],
A
ABC nde [DE] ⊥ [AC], [BC] ⊥ [AC], |AD|=6cm,
10
|DB|=4cm ve |BC|, |DE| ndan
cm fazla
olduğuna göre |DE| kaç cm dir? 3
7.
A
x
D
4 cm
E
4 cm
8 cm
H
C
B
ABC nde [AB] ⊥ [AC] ve [AH] ⊥ [BC] dır.
|AH|=4cm, |HC|=8cm olduğuna göre
|AB|=x kaç cm dir?
8.
A
3 cm
ABC nde [DE] // [BC], m(DBE)=m(EBC),
|BD|=4cm, |BC|=12cm olduğuna göre
|AD|=x kaç cm dir?
13.
A
D
F
10 cm
B
C
ABC nde |AD|=5cm, |DB|=3cm, |BE|=2cm,
|EC|=10cm, |AE|=8cm olduğuna göre
|DC|=x kaç cm dir?
9.
X
20
P
3
C
ABC nde [AB] ⊥ [AC] , DEFG kare, |AG|=7cm,
|BD|=9cm olduğuna göre A(DEFG) kaç cm2
dir?
14.
A
8
E
B
9
R
F
E
A
B
7 cm
G
9 cm
B 2 cm E
D
C
12 cm
5 cm
D
B
a
ABCD dik yamuğunda köşegenler dik
kesişiyorsa h uzunluğunu, a ve c cinsinden
bulunuz.
12.
A
B
C
h
C
x
c
H
E
B
C
D
6 cm
D
E
D
5 cm
C
2 K
6
N
D
C
ABC nde [DE] // [BC], A(APE)=3cm ,
A(DBRP)=20 cm2, A(PRCE) = 9cm2 olduğuna
göre A(ADP)=x kaç cm2 dir?
2
106
ABD ve BDC nde [AB] ⊥ [AD], [BC] ⊥ [CD],
[AN] ⊥ [BD], [KC] ⊥ [BD], |AN|=8cm,|BK|=2cm,
|KC|=6cm olduğuna göre |KN| kaç cm dir?
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
PROJE
Bir eşkenar üçgen üzerinde aşağıdaki işlemleri yapınız.
1. İşlem
2. İşlem
3. İşlem
4. İşlem
Birinci işlem: Bir kenarı üç eşit parçaya ayırınız.
İkinci işlem : Ortadaki parça taban olacak şekilde ilk üçgenin dışında bir eşkenar üçgen çiziniz.
Üçüncü işlem: Bir önceki işlemdeki eşkenar üçgenin tabanı olan ortadaki parçayı siliniz.
Dördüncü işlem: Önceki işlemleri diğer kenarlar üzerinde de yapınız.
Bu şekilde elde edilen kenarlar üzerinde aynı işlemler yapıldığında;
+ =
+ =
1. Kar Tanesi
2. Kar Tanesi
oluşur. Bu biçimde oluşturulan şekle Koch (Koh) Kar Tanesi adı verilir. İşlem sayılarını artırarak
değişik boyutlarda Koh kar taneleri oluşturabilirsiniz.
Dördüncü işlemde oluşan kar tanesini birinci kar tanesi diye isimlendirirsek n inci
kar tanesinin kenar sayısını, çevre uzunluğunu ve alanını veren bir genellemeye ulaşmaya
çalışınız.
ÜNİTE SONU ÖLÇME SORULARI
1. Eşkenar dörtgen ile kare arasındaki fark nedir?
2. Hangi dörtgenlerde köşegen uzunlukları birbirine eşittir?
3. Hangi dörtgenlerde köşegenler her zaman birbirine diktir?
4. Herhangi bir dörtgenin kenarlarının orta noktaları birleştirilerek hangi dörtgen elde edilir?
5. ABCD paralelkenarında AC köşegenini çiziniz. B ve D noktalarından AC köşegenine
indireceğiniz dikme uzunlukları için ne söyleyebilirsiniz?
6. Her bir iç açısının ölçüsü 1800 den küçük olan çokgen ....... bükey çokgendir.
7. En az bir iç açısının ölçüsü 1800 den büyük olan çokgen ........bükey çokgendir.
8. Bir düzgün çokgenin iç açısının ölçüsü en az kaç derece olabilir?
107
2. ÜNİTE
13.
9.
d2
d1
d3
C
D
1500
6 cm
A
1200
d4
x
400
Yukarıdaki şekilde d1, d2, d3 ve d4 doğrularının
oluşturduğu bazı açı ölçüleri verilmiştir. x kaç
derecedir?
A) 45
B) 50 C) 60 D) 75
E) 90
2 cm
ABCD dörtgeninde [DE]//[BC] ve
[DA] ⊥ [AB] dir. |DA|=6cm, |AE|=2cm ve
|EB|=4cm ise A(AECD) kaç cm2 dir?
A) 18 B) 16
C) 14
D) 12
E) 10
14.
D
10.
C
F
K
D
E
x
A
C
300
F
A
B
ABCD paralelkenar, A, F ve E doğrusaldır.
|EF|=|EC| , m(DAE)=m(EAB) ve m(FCB)=300
ise m(ADE)=x kaç derecedir?
A) 120 B) 130 C) 140 D) 150 E) 160
B
4 cm
E
B
E
ABCD karesinin bir kenar uzunluğu 8 cm dir.
E ve F bulundukları kenarların orta noktaları
olduğuna göre A(ADK) kaç cm2 dir?
B) 8
C) 16 D) 32
E) 64
A) 4
5
5
5
5
5
15.
D P R S
T U C
11.
D
C
A K
L
M
N
B
ABCD paralelkenarında
|DP|=|PR|=|RS|=|ST|=|TU|=|UC| ve
A
B
ABCD ikizkenar yamuğunda [AB] // [DC] dir.
m(DCB)=2.m(DAB) ise m(ADC) kaç derecedir?
A) 110 B) 120 C) 130 D) 140 E) 150
12.
D
E
A
C
F
16.
A
D
2x+3
E
B
Yukarıdaki ABCD paralelkenarında
[EC] ⊥ [BF] dir. |EC|=16cm, |BF|=2x+3 cm dir.
A(ABCD)=176cm2 ise x kaç cm dir?
A) 1
B) 2
C) 3
D) 4
E) 5
108
A(KNSR)
|AK|=|KL|=|LM|=|MN|=|NB| ise
A(ABCD)
oranı kaçtır?
23
19
17
23
19
A)
B)
C)
D)
E)
60
60
30
30
30
B
F
C
Şekilde ABD ≅ BCE ≅ CAF olduğuna göre
DEF nın ölçüsü kaç derecedir?
A) 30 B) 45
C) 60
D) 75
E) 90
ÇOKGENLER VE DÜZLEMDE KAPLAMALAR
17.
21.
6 3
D
B
A
C
C
300
A
D
B
18 3
Yukarıdaki ABCD ikizkenar yamuğunda
|AD|=|BC|, m(DAB)=300, |DC|= 6 3 cm ve
|AB|=18 3 cm ise A(ABCD) kaç cm2 dir?
A) 36 3 B) 48 3 C) 56 3
D) 60 3 E) 72 3
18.
4
F
D
300
E
AB // DE, A, C, E ve B, C, D doğrusaldır.
| AC | 4
= , |BD|=27cm olduğuna göre |BC|=x
| CE | 5
kaç cm dir?
A) 3
B) 6
22.
C) 9
D
E
D) 12
E) 15
C
1100
1200
C
E
x
A
B
8 3
Yukarıdaki şekilde ABCD dikdörtgen, A, F ve E
noktaları doğrusaldır. m(EFC)=300, |EF|=4cm
ve |AB|= 8 3 cm ise A(ABCD) kaç cm2 dir?
B) 36 3
C) 48 3
A) 32 3
D) 60 3
E) 72 3
19.
A
4
2
D
3
6
C
D
1300
E
x
C
Yukarıdaki ABC nde m(ADE)=m(ACB),
|AD|=4cm, |AE|=3cm, |DB|=2cm, |DE|=6cm,
|EC|=x cm ve |BC|=y cm ise x+y kaç cm
olur?
A) 17 B) 16 C) 15 D) 14
E) 13
20.
A
ABCD dörtgeninde m(ADC) = 1200
m(DCB)=1100 dir. [BE] ve [AE] açıortay ise
m(AEB) = x kaç derecedir?
A) 100 B)110 C) 115 D) 120 E) 125
23.
E
y
E
B
x
B
D
A
6
10
16
C
A
300
F
B
ABCD dörtgeninde m(DAB) = 300,
m(DCB) = 1300, m(ADE) = m(CDE) ,
m(ABE) = m(CBE) ise m(FEB) = x kaç derecedir?
A) 50
B) 60 C) 70 D) 80 E) 90
24. Escher (Eşer) ‘in aşağıdaki eserinde hangi
dönüşümler vardır?
F
B
Yukarıdaki ABCD dörtgeninde
[AB]//[CD]//[EF] dir. |DC|=6cm, |EF|=10cm ve
| CF |
|AB|=16cm ise
oranı kaçtır?
3 | BF | 4
5
6
2
A)
B)
C)
D)
E)
4
5
6
7
3
109
3. ÜNİTE
DİK PRİZMALAR
VE PİRAMİTLER
+
+
+
+
İzometrik ve Ortografik Çizimler ve Hacimleri
Dik Prizma ve Piramit Kavramları
Dik Prizma ve Düzgün Piramit Yüzey Alanları Bağıntıları
Dik Prizma ve Düzgün Piramit Hacim Bağıntıları
Muhteşem yapıları çizerken kullanılan
basit geometrik şekilleri inceleyiniz.