7 – Transformatörler
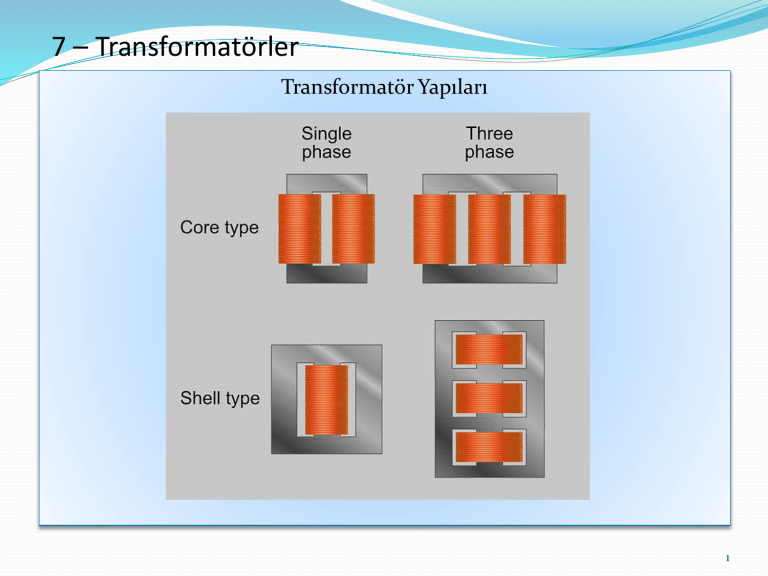
Transformatör Yapıları
1
7 – Transformatörler
Transformatör Yapıları
2
7 – Transformatörler
Transformatör Yapıları
3
7 – Transformatörler
Transformatör Yapıları
4
7 – Transformatörler
Transformatör Yapıları
1. Shell Transformatör
Shell tür transformatörde, düşük gerilimli sargı içe yüksek gerilimli sargı ise dışa sarılır.
Bunun amacı;
1. Yüksek gerilimli sargıyı nüveden uzak tutarak yalıtım problemlerine mahal vermemek.
2. Hava aralığı yolunu artırarak kaçak akıyı azaltmak.
*Bu yüzden yüksek gerilimler için shell tür transformatörler daha uygundur.
*Doğal soğutma performansı düşüktür.
2.Çekirdek Transformatörler
*Düşük gerilimlerde kullanılır, yüksek gerilimler için uygun değildir.
*Doğal soğutma performansı yüksektir çünkü sargılar iki farklı bacağa sarılır.
5
7 – Transformatörler
Transformatör Çeşitleri
Primer ve Sekonder Gerilimlerinin Durumuna Göre;
1. Yükselten Transformatör
2. Düşüren Transformatör
Nüve Şekline Göre;
1. Çekirdek Transformatör
2. Shell Transformatör
Faz Sayısına Göre
1. Tek Fazlı Transformatör
2. Çok Fazlı Transformatör
Çalışma Bölgesine Göre
1. Güç Transformatörleri
2. Enstrüman Transformatörleri
a.) Akım transformatörleri
b.) Gerilim transformatörleri
3. Pals Transformatörleri (Sayısal ve Telekominikasyon devrelerinde)
4. Radyo-Frekans (RF) Transformatörleri
5. Ses Transformatörleri (Yükselteç devrelerinde)
6. Ev Kullanımı için Düşüren Tip Klasik Transformatör
6
7 – Transformatörler
Enerji İletimi
7
7 – Transformatörler
Enerji İletimi
8
7 – Transformatörler
İdeal Transformatör
1. Primer ve Sekonder sargılarının elektriksel direnci sıfır kabul edilir. Bu yüzden sargı bakır kayıpları sıfır çıkar. Ayrıca dirençlerdeki
gerilim düşümü de ihmal edilmiş olmaktadır. Böylece primer sargısına uygulanan gerilim, primer sargısında indüklenen gerilime
eşit olur.
2. Primer ve Sekonder sargılarındaki kaçak akının sıfır olduğu kabul edilir. Böylece, primer sargısının ürettiği bütün akı değeri
nüvede mıknatıslama akısı olarak dolaşır.
3. Nüvede manyetik doyma, histeresis ve eddy etkilerinin olmadığı kabul edilir. Bu durum demir kayıplarının sıfır olduğunu
göstermektedir. (ic=0)
4. Nüvenin permabilitesinin sonsuz olduğu (𝜇 = ∞) kabul edilir. Bu durum nüve relüktansının sıfır endüktansların sonsuz olmasına
yol açar. Böylece mıknatıslama akımı da sıfır olmuş olur. (im=0)
5. Boşta çalışma akımı sıfır olmuş olur. (i0=im+ic=0)
6. Demir ve bakır kayıpları sıfır olduğu için verim %100’dür.
P (L P ) S (L S ) m (L m )
Fnet m m 0 0
P (L P )
S (L S )
+
iP
VP Vm sin( t)
-
LP
NP
m (L m )
+
-
eP
eS
-
+
iS
LS
NS
RL
VS
+
0
9
7 – Transformatörler
İdeal Transformatör – Giriş ve Çıkış Güçleri
P (L P ) S (L S ) m (L m )
Fnet m m 0 0
P (L P )
S (L S )
+
iP
VP Vm sin( t)
LP
NP
-
m (L m )
+
-
eP
eS
-
+
a
iS
LS
NS
RL
+
0
iP
LP
LS
NP
NS
VS
Np
Ns
V p (t)
Vs (t)
is (t )
eP (t) N p
a
eS (t) N s
N p i p (t ) N s is (t )
i p (t )
iS
Ns 1
Np a
Pin V p I p cos( p )
Pout Vs I s cos( s )
VP
VS
RL
p s
10
7 – Transformatörler
İdeal Transformatör – Güç Eşitliği
P (L P ) S (L S ) m (L m )
Fnet m m 0 0
P (L P )
S (L S )
+
iP
VP Vm sin( t)
-
LP
NP
Pin V p I p cos( p )
Pout Vs I s cos( s )
m (L m )
+
-
eP
eS
-
+
LS
NS
0
p s
iS
RL
VS
+
V
Pout P aI p cos( ) Pin
a
V
Qout P aI p sin( ) Qin
a
V
Sout P aI p Sin
a
11
7 – Transformatörler (S.Chapman)
İdeal Transformatör – Empedans Dönüşümü
ZL
VL
IL
ZL
Vs
V
Z L' P
Is
IP
V p aVs
Ip
Z L'
Is
a
Vp
Ip
aVs
a2ZL
Is
a
12
7 – Transformatörler
İdeal Transformatör – Empedans Dönüşümü
Yandaki devrede trafonun empedans dönüşümü
özelliği kullanılarak, yükseltecin çıkış direnci ve
hoparlörün giriş direnci birbirine eşitlenmektedir.
Böylece maksimum güç aktarımı sağlanabilmekte
dir. Yüksek güçlü amplifikatörlerin büyük ve ağır
olmalarının ana sebebi de budur.
13
7 – Transformatörler
İdeal Transformatör – Empedans Dönüşümü
.
14
7 – Transformatörler (S.Chapman)
İdeal Transformatör – Empedans Dönüşümü
15
7 – Transformatörler
İdeal Transformatör – Empedans Dönüşümü
a.) I line I G I load
V
4800
90.8 37.8
Z line Z load 4.18 j 3.24
Vload I line Z load 90.8 37.8 536.9 454 0.9
Ploss I line Rline 90.8 0.18 1484W
2
2
'
b.) Z load
a 2 Z load 400 j 300
Z eq 400.18 j 300.24
Z 'eq a 2 Z eq 0.01 400.18 j 300.24 5.00336.88
4800
95.94 36.88
5.00336.88
N P1 I G N S 1 I line I line 9.594 36.88
IG
N P 2 I line N S 1 I load I load 95.94 36.88
Vload I load Z load 479.7 0.01
Ploss I line Rline 9.594 0.18 16.7W
2
2
16
7 – Transformatörler (S.Chapman)
İdeal Transformatör – Empedans Dönüşümü
17
7 – Transformatörler
Gerçek Transformatör
Çalışılan konular:
*Trafo parametrelerinin bulunması
*Trafo kayıplarının bulunması
*Trafo veriminin bulunması
*Trafonun maksimum verimde çalışma koşullarının sağlanması
*Trafo regülasyonunun bulunması
PS (L PS ) SP (L SP ) m (L m )
*Üç fazlı trafolarda bağlantı şekilleri
Fnet m
PS (L PS )
SP (L SP )
+
iP
RP
+
VP Vm sin( t)
-
m (L m )
LP (L LP )
ePS
LP
NP
RS
-
eSP
+
-
l
A
iS
RL
LS
NS
-
VS
+
LS ( LLS )
18
7 – Transformatörler
Gerçek Transformatör
1. Kaçak akılar var. (Sargı akımları ile orantılıdır)
2. Sargıların elektriksel direnci var.
3. Histeresis ve eddy etkisi ile manyetik doyum var.
4. Nüvenin relüktansı var.
5. Sıfırdan büyük bir boşta çalışma akımı var.
6. Verim %100’ün altında.
PS (L PS ) SP (L SP ) m (L m )
Fnet m
PS (L PS )
SP (L SP )
+
iP
RP
+
VP Vm sin( t)
-
m (L m )
LP (L LP )
ePS
LP
NP
RS
-
eSP
+
-
l
A
iS
RL
LS
NS
-
VS
+
LS ( LLS )
19
7 – Transformatörler
Gerçek Transformatör
1. Kaçak akılar var. (Sargı akımları ile orantılıdır)
2. Sargıların elektriksel direnci var.
3. Histeresis ve eddy etkisi ile manyetik doyum var.
4. Nüvenin relüktansı var.
5. Sıfırdan büyük bir boşta çalışma akımı var.
6. Verim %100’ün altında.
20
7 – Transformatörler
Gerçek Transformatör – Manyetik Bağlantı
LLP
LPS
LSP
LLS
LLP
LLS
im
Lm
Lm
Mantetik bağlantı devresi
LP LPS LLP
LS LSP LLS
Lm LPS LSP
Lm k LP LS
21
7 – Transformatörler
Gerçek Transformatör – Mıknatıslama Endüktansı
iP
RP
LLP
LPS
LSP
RS
LLS
iS aiP
im
ePS
VP
eSP
Lm
1
eSP
a
VS
RL
Mantetik bağlantı devresi
VP
iP
RP
*
X LS
a 2 X LS
X LP
RS* a 2 RS iS* iS / a
im
ePS
Lm
*
eSP
aeSP
LP LPS LLP
RL* a 2 RL
VS* aVS
LS LSP LLS
Lm LPS LSP
Lm k LP LS
22
7 – Transformatörler
Gerçek Transformatör – Vektörel Diyagramlara Hazırlık
P PS LP
dP
S SP LS
d S
PS SP m
dm
1.Kaçak akilar çok küçük ise;
PS LP & SP LS
dt
d
d
VS (t ) N S SP N S LS
dt
dt
VS (t ) eSP (t ) eLS (t )
dt eP (t )
d
N S m eS (t )
dt
ePS (t ) N P
a
eSP (t ) N S
LP LS 0
P PS
S SP
VP (t ) N P
VS (t ) N S
di
VP (t ) LP P
dt
d
d
VP (t ) N P PS N P LP
dt
dt
di
di
VP (t ) LPS P LLP P
dt
dt
VP (t ) ePS (t ) eLP (t )
di
VS (t ) LS S
dt
d
d
VS (t ) N S SP N S LS
dt
dt
di
di
VS (t ) LSP S LLS S
dt
dt
VS (t ) eSP (t ) eLS (t )
LP LPS LLP
LS LSP LLS
dt
d
d
VP (t ) N P PS N P LP
dt
dt
VP (t ) ePS (t ) eLP (t )
NP
2.Nüvenin relüktansi çok küçük ise;
0
Fnet N PiP N S iS m 0
P S m 0;
FP FS
Bu trafo ideale çok yakindir;
VP (t ) eP (t ) N P
a
VS (t ) eS (t ) N S
Sadece renkli formüller önemli.
23
7 – Transformatörler (S.Chapman)
Gerçek Transformatör – Mıknatıslama akımı
24
7 – Transformatörler (S.Chapman)
Gerçek Transformatör – Mıknatıslama akımı
25
7 – Transformatörler (S.Chapman)
Gerçek Transformatörler – Eddy akımları ve Histeresis Etkisi
26
7 – Transformatörler
Gerçek Transformatör – Boşta Çalışma Akımı
27
7 – Transformatörler
Gerçek Transformatörler – Boşta Çalışma Akımı
28
7 – Transformatörler
Gerçek Transformatörler – Boşta Çalışma Akımı
http://en.wikipedia.org/wiki/Transformer
29
7 – Transformatörler
Gerçek Transformatörler – Nüve Kayıpları (M. Rashid)
30
7 – Transformatörler
Gerçek Transformatörler – Boşta Çalışma Akımı
*Sinüsoidal olmayan bir boşta çalışma akımı mevcuttur. Bu akımda 3. harmonik baskındır.
*Eğer doğrusal bir yük besleniyorsa sekonderden çekilen akım sinüsoidal olur. Dolayısıyla,
primerden çekilen yük akımı bileşeni (sekonder akımı bileşeni) de sinüsoidal olur. Yük akımı
bileşeni boşta çalışma akımından çok daha büyük olduğu için, boşta çalışma akımının sinüsoidal
olmayan durumunun toplam primer akımına bağıl etkisi çok düşük çıkar. Bu yüzden doğrusal yük
altında çalışan trafolarda primer akımı hemen hemen tam sinüsoidaldir.
*Üç fazlı trafolarda 3. harmonik fazlar arasında yok olmaktadır. Bu yüzden 3 fazlı trafolarda boşta
çalışma akımları hemen hemen sinüsoidal kabul edilir.
Soru: Eşdeğer kullanılmış iki trafo bulunsun. Hangisinin daha yaşlı olduğunu en kolay nasıl anlarız.
Cevap: Boşta çalışma akımının genliği ve dalga şeklinden…
31
7 – Transformatörler
Gerçek Transformatör – Tam Model
VP
iP
RP
X LP
X LS
iS* iS / a
RS
iS
i0
ic
im
Rc
X m ePS
eSP
VS
RL
NP : NS
ideal trafo
32
7 – Transformatörler
Gerçek Transformatör – Primere ve Sekondere İndirgenmiş Tam Modeller
RP
iP
*
X LS
a 2 X LS
X LP
RS* a 2 RS iS* iS / a
i0
ic
ePS
VP
im
*
X m eSP
aeSP
Rc
iP* aiP
R RP / a
*
P
VP* VP / a
RL* a 2 RL
VS* aVS
*
X LP
X LP / a 2
X LS
iS
i0
2
*
ePS
ePS / a
RS
ic
im
Rc
X m eSP
RL
VS
33
7 – Transformatörler
Gerçek Transformatör – Primere ve Sekondere İndirgenmiş Yaklaşık Modeller
RP
iP
*
X LS
a 2 X LS RS* a 2 RS iS* iS / a
X LP
i0
VP
ic
im
Rc
Xm
*
ePS eSP
aeSP
1
VP
a
RL* a 2 RL
VS* aVS
*
RP* RP / a 2 X LP
X LP / a 2
iP* aiP
X LS
RS
iS
i0
ic
im
Rc
Xm
*
ePS
ePS / a eSP
VS
RL
34
7 – Transformatörler
Gerçek Transformatör – Polarite Deneyi
35
7 – Transformatörler
Gerçek Transformatör – Boşta Çalışma
VP
iS* 0
iP i0
ic
0
i0
m
im
iP
RP
*
X LS
a 2 X LS
X LP
RS* a 2 RS iS* iS / a
i0
eS
ic
eP
VP
ePS
Rc
im
*
X m eSP
aeSP
RL* a 2 RL
VS* aVS
36
7 – Transformatörler
Gerçek Transformatör – Boşta Çalışma Deneyi
VP
iS* 0
iP i0
ic
0
Pc P0 iP2 RP
i0
im
P0
pf
V0i0
0 cos 1
m
e0 V0 i0 RP
Pc P0 iP2 RP
eS
eP
P0
pf
V
i
00
0 cos 1
Ye
i0
0
V0
1
Rc
Ye cos( 0 )
Xm
1
Ye sin( 0 )
e02
RC
Pc
ic
Pc
e0
im i02 ic2
e
Xm 0
im
a
e0
VS
Xm
2 f
LPS aLm
Lm
LSP
1
Lm
a
37
7 – Transformatörler
Gerçek Transformatör
– Yüklü Çalışma
VP
jX LP iP
iP
RP
RP iP
VP
P
iP
*
S
i
X
i S* i S / a
LP
LS
RS
iS
i0
Z P iP
ePS
X
ic
im
Rc
X
m
e SP
ePS
VS
RL
N
P
:N
S
id e a l tra fo
i0
m
VP eP iP RP jiP X LP
VS eS i2 RS jiS X LS
S
iS
VS
iS RS
iS Z S
jX LS iS
eSP
38
7 – Transformatörler
Gerçek Transformatör – Yüklü Çalışma
VP
VP eP iP RP jiP X LP
Z P iP
ePS e
*
SP
S
P
i0
V
m
RP
*
X LS
a 2 X LS
X LP
RS* a 2 RS iS* iS / a
i0
ic
VP
* *
jX LS
iS
iS* RS*
iP
iP
*
VS eS* iS* RS* jiS* X LS
RP iP
iS* Z S*
*
S
iS*
jX LP iP
ePS
Rc
im
*
X m eSP
aeSP
RL* a 2 RL
VS* aVS
39
7 – Transformatörler
Gerçek Transformatör – Kısa Devre Deneyi
Z eq
X eq
iSC
X LP
*
X LS
a 2 X LS
Req
RP
RS* a 2 RS
P
pf cos 1 SC
VSC iSC
V
Z eq SC
iSC
R e q Z eq cos( )
VSC
X eq Z eq sin( )
*
X LP X LS
LLP X LP / 2 f
X LS X L*S / a 2
LLS X LS / 2 f
40
7 – Transformatörler
Gerçek Transformatör – Gerilim Regülasyonu
Req
iP* aiP
X eq
iS
i0
1
VP
a
ic
im
Rc
Xm
VS
VP / a
iS Z eq
iS X eq
VS
S
%VR
iS Req
iS
%VR
VSnl VSfl
VSfl
100
VP / a VSfl
VSfl
100
41
7 – Transformatörler
Gerçek Transformatör – Gerilim Regülasyonu ve Verim
*Boşta çalışma deneyinden demir kayıplarını ve ilgili parametreleri bul.
*Kısa devre deneyinden eşdeğer empedans ve bileşenlerini bul.
*Isanma=S/Vs’den sekonder akımının tam yükteki değerini bul.
*Belirli bir sekonder (yük) güç katsayısı (cos(θS)) için VP/a değerini hesapla.
*Veya belirli bir güç katsayısı (cos(θS)) için VS değerini hesapla.
*%VR’yi hesapla.
*Po=VSiScos(θS) çıkış gücünü hesapla.
*Pcu=IsanmaReq bakır kayıplarını hesapla.
*Pin=Po+Pv+Pc giriş gücünü hesapla.
*Verimi hesapla.
Req
X eq
iP* aiP
i0
1
VP
a
ic
im
Rc
Xm
iS
VS
42
7 – Transformatörler
Gerçek Transformatör - Kayıplar
Po VS I S cos(S )
Pin VP I P cos( P )
PPcu PScu
Pfe
Pc Pfe
Pv PPcu PScu
Po
Po
Pin Po Pc Pv
43
7 – Transformatörler
Gerçek Transformatör – Kısa Devre Deneyi
Örnek 2.2
S 20kVA
8000 / 240V
50 Hz
(Sekonderden uygulaniyor)
V0 240V
240
1.3732rad
489 2.5
cos 1
Z eq
VSC
195.61.3732
iSC
a 8000 / 240 33.33
R e q Z eq cos( ) 195.6cos(1.3732) 38.3988
X eq Z eq sin( ) 195.6sin(1.3732) 191.7939
i0 7.133 A
*
X LP X LS
191.7939 / 2 95.8969
P0 400W
LLP 95.8969 / (2 50) 0.305H
LLS 95.8969 / (a 2 2 50) 0.0002746 H
(Primerden uygulaniyor)
VSC 489V
iSC 2.5 A
R p Rs* R e q / 2 38.4 / 2 19.2
Rs 19.2 / a 2 19.2 / 33.332 0.01728
PSC 240W
44
7 – Transformatörler
Gerçek Transformatör – Boşta Çalışma Deneyi
Örnek 2.2
S 20kVA
8000 / 240V
50 Hz
(Sekonderden uygulaniyor)
V0 240V
i0 7.133 A
P0 400W
Pc Po 400W
400
0 cos
1.33rad
240 7.133
e0 V0 240V
1
e02 2402
Rc
144
Pc 400
ic
Pc 400
1.666A
e0 240
(Primerden uygulaniyor)
VSC 489V
im i02 ic2 6.937A
Xm
e0
34.597
im
X m 34.597
2 f
2 50
Lm 0.110H
Lm
LPS aLm 3.67H
LSP
1
Lm 0.00329H
a
iSC 2.5 A
PSC 240W
a.) Geri kalan tüm parameterlerin değerlerini hesaplayınız.
b.) Primere indirgenmiş tam modeli çıkartınız.
NOT: Diğer modeller de (örneğin tam model) sorulabilirdi.
45
7 – Transformatörler
Gerçek Transformatör – Endüktans ve Direnç Hesapları
Örnek 2.2
S 20kVA
8000 / 240V
50 Hz
(Sekonderden uygulaniyor)
V0 240V
i0 7.133 A
P0 400W
LP LPS LLP
LP 3.67 0.305 3.975H
LS LSP LLS
LPS aLm 3.67H
LSP
1
Lm 0.00329H
a
LS 0.00329 0.0002746
LS 0.0036H
k
Lm
0.11
0.9255
LP LS 0.1175
(Primerden uygulaniyor)
VSC 489V
iSC 2.5 A
PSC 240W
46
7 – Transformatörler
Gerçek Transformatör – Primere İndirgenmiş Tam Model
iP
19.2
j 95.8969
j 95.8969
iS*
i0
ic
144
19.2
im
j 34.5973
VS* aVS
47
7 – Transformatörler
Gerçek Transformatör – Gerilim Regülasyonu ve Verim Hesabı
Tam yük altında, 0.8 sekonder geri güç faktörü için %VR ve Ƞ değerini hesaplayınız.
Req
iP* aiP
X eq
iS
VP / a 251.118V
i0
1
VP
a
ic
im
Rc
Xm
iS Z eq
0.0389rad
VS
VS 240V
iS X eq
iS Req
0.644rad
iS 83.33 A
20000
83.33-0.644A
240
Rs RP / a 2 0.01728 19.2/33.332
isanma
Req
VP / a 250.928 j9.769
VP / a 251.1180.0389
R e q 0.0345
X eq =191.7939/33.332 0.1725
VP / a 240 0.0345 83.33-0.644+j0.1725 83.33-0.644
VP / a 240 2.8748-0.644+14.37440.9268
VP / a 240 2.298 j1.726 8.63 j11.495
%VR=
251.118 240
100 %4.63
240
48
7 – Transformatörler
Gerçek Transformatör – Gerilim Regülasyonu ve Verim Hesabı
Tam yük altında, 0.8 sekonder geri güç faktörü için %VR ve Ƞ değerini hesaplayınız.
1
VP
a
Req
iP* aiP
X eq
iS
VP / a 251.118V
i0
ic
im
Rc
Xm
iS Z eq
0.0389rad
VS
VS 240V
0.644rad
iS X eq
iS Req
iS 83.33 A
Po 240 83.33 cos(0.644) 16000 W
Pv 83.332 0.0345 239.56W
Pc 400W
Pin Po Pv Pc 16000 400 239.56
Pin 16639.56W
16000 16639.56 100 %96.15
49
7 – Transformatörler
Gerçek Transformatör – Maksimum Verim noktası
0.8 geri güç faktörü için, verimin maksimum olduğu kVA yüklenme değerini ve bu yükteki sekonder akımını hesaplayaınız.
1
VP
a
Req
iP* aiP
X eq
iS
Pv iS2 0.0345
i0
ic
im
Rc
Xm
Pc 400W
Pv Pc
VS
400
107.6A
0.0345
S 240 107.6 25825VA
iS
Po 240 107.6 cos(0.644) 20651W
Pin Po Pv Pc
Pin 20651 2 400 21451W
max 20651 21451 100 %96.27
50
7 – Transformatörler
Gerçek Transformatör – Maksimum Verim noktası
Soru: Bu trafo maksimum verimde çalışabilir mi?
1
VP
a
Req
iP* aiP
X eq
iS
Pv iS2 0.0345
i0
ic
im
Rc
Xm
Pc 400W
Pv Pc
VS
400
107.6A
0.0345
S 240 107.6 25825VA
iS
Po 240 107.6 cos(0.644) 20651W
Pin Po Pv Pc
Pin 20651 2 400 21451W
max 20651 21451 100 %96.27
Cevap: Bir trafonun maksimum verimde çalışabilmesi için maksimum verim noktasının trafounun VA cinsinden güç
değerinin altında bulunması gerekir. Dolayısıyla buradaki trafo maksimum verimde çalışamaz.
51
7 – Transformatörler
Gerçek Transformatör – Örnek
4kVA 200/400V bir trafonun;
primere indirgenmis esdeger direnci 0.15' dur.
Pfe =60W olduguna göre:
a.)0.9 geri güç faktöründe tam yükte nedir?
b.)0.8 ileri güç faktörleründe yari yükte nedir?
200
0.5
400
0.15
Req
0.6
0.52
4000
isanma
10 A
400
4000 0.9
100
4000 0.9 102 0.6 60
%96.77
0.5 4000 0.8
b.)
100
0.5 4000 0.8 52 0.6 60
%95.52
a.)a
Kitaptan çalışma ödevi: Örnek 2.5
52
7 – Transformatörler
Gerçek Transformatör – Maksimum Verim Koşulları
iS2 R e q Pc
d
0
d (IS )
max
iSanma
iS m
Pv Pc
VS iS cos(S )
VS iS cos(S ) iS2 R e q Pc
Pc
Req
iS m
iS m
I S ( A)
iSanma
VS iS m VS iSanma
1
Pc
Req
iSanma
kVA n kVA
Pc
Pvanma
Pc
Pvanma
P
i
c
2
Sanma
iS m iSanma
Req
Pc
Pvanma
VS iS cos(S )
0
2
V
i
cos(
)
i
R
P
S
S
eq
c
SS
VS iS cos(S ) iS2 R e q Pc did VS iS cos(S ) VS iS cos(S ) did VS iS cos(S ) iS2 R e q Pc 0
S
S
d
diS
V i
S S
cos(S ) iS2 R e q Pc VS cos(S ) VS iS cos(S ) VS cos(S ) 2iS R e q 0
iS2 R e q Pc
Pv Pc
53
7 – Transformatörler
Gerçek Transformatör - Örnek
100kVA’lık bir trafonun anma yükünde demir kayıpları 1.2kW, bakır kayıpları ise 1.5kW’tır.
a.)Maksimum verim için trafo kaç kVA’da çalışmalıdır.
b.)Birim güç faktöründe tam yükte trafonun maksimum verimi nedir?
a.)kVA n kVA
kVA n 100
Pc
Pvanma
1.2
89.4427 kVA
1.5
b.) Pc Pv 1.2kW
VS iS 1
100
VS iS 1 Pv Pc
100
100 %97.66
100 2.4
54
7 – Transformatörler
Ayarlı Transformatör (Ototrafosu)
55
7 – Transformatörler
Ayarlı Transformatör (Ototrafosu)
Klasik Trafolara (Nüveli) Göre Üstünlükleri:
*Daha az iletken gereketirirler.
*Daha yüksek verime sahiptirler.
*VR performansları daha iyidir.
*Güç yoğunlukları daha yüksektir.
*Daha küçük bir mıknatıslama akımı çekerler.
NOT: yukarıdaki üstünlükler dönüşüm oranı büyüdükçe ortadan kalkmaktadır.
Klasik Trafolara (Nüveli) Göre Sakıncaları:
*Giriş ve çıkış arasında elektriksel bağlantı vardır, yani yalıtım yoktur.
*Ototrafoları güvenli değildir, genel kullanıma uygun değildir.
*Kısa devre akımları daha yüksektir.
56
7 – Transformatörler
Ölçü (Enstrüman) Transformatörleri
1. Akım Transformatörleri:
Yüksek akım değerlerindeki bilgileri işlemek için veya ölçmek için bu yüksek değerlerin uygun
düşük değerlere düşürülmesi gereklidir. Bu yüzden akım trafolarına ihtiyaç duyulur. Devreye seri
bağlanır, dolayısıyla primer direnci çok küçüktür.
Sekonderi bir ampermetreye bağlanacak şekilde “yani sekonderi kısa devre” tasarlanırlar. Bu
yüzden, bir akım trafosunun ucu asla açıkta bırakılmaz. Aksi takdirde tahrip olurlar. Eğer akım
trafosunun uçları kullanılmayacaksa bile kısa devre edilir.
***Sargılı ve Bara olmak üzere iki farklı yapıda imal edilirler.
***Sekonder sargının bir ucu topraklanır. (Müstakil veya müşterek)
***Koruma devrelerinde 3 sınıfı, sayaçlarda 0.2-0.5 sınıfı, ölçü
aletlerinde 1 sınıfır kullanılır.
57
7 – Transformatörler
Ölçü (Enstrüman) Transformatörleri
58
7 – Transformatörler
Ölçü (Enstrüman) Transformatörleri
59
7 – Transformatörler
Ölçü (Enstrüman) Transformatörleri
60
7 – Transformatörler
Ölçü (Enstrüman) Transformatörleri
61
7 – Transformatörler
Ölçü (Enstrüman) Transformatörü
2. Gerilim Transformatörleri:
Akım trafolarında olduğu gibi yüksek gerilim değerlerini uygun değerlere düşürerek işlemek veya
ölçmek için kullanılırlar. Devreye paralel bağlanırlar, dolayısıyla primer dirençleri çok yüksek olacak
şekilde tasarlanırlar.
Gerilim trafoları sekonderi bir voltmetreye bağlanacak şekilde “yani boşta çalışmak üzere”
tasarlanmış trafolardır. Sekonder uçları kesinlikle kısa devre edilmemelidir. Aksi takdirde tahrip
olurlar.
***Bara tipinde imal edilemezler.
***Koruma devrelerinde 3 sınıfı, sayaçlarda 0.2-0.5 sınıfı, ölçü
aletlerinde 1 sınıfı kullanılır.
***Faz-Toprak ve Faz-Faz şeklinde imal edilirler.
62
7 – Transformatörler
Ölçü (Enstrüman) Transformatörü
63
7 – Transformatörler
Ölçü (Enstrüman) Transformatörü
64
7 – Transformatörler
Ölçü (Enstrüman) Transformatörü
65
7 – Transformatörler
Ölçü (Enstrüman) Transformatörü
66
7 – Transformatörler
3 Fazlı Transformatörler
Üç fazlı transformatörler genellikle güç iletiminde kullanılmaktadır.
İki farklı şekilde kullanımı vardır.
1.
2.
Üç adet tek fazlı transformatörün uygun bağlantısı ile elde edilebilir.
Ortak bir nüve üzerine üç fazlı olarak da imal edilebilir.
İlk kullanım çözüm amaçlıdır ikinci kullanım ise yaygın durumdur.
Her iki şekilde de iki adet üç fazlı trafo sistemimiz var olduğunu kabul edelim. Ayrıca, bir faza
gerilim gelmediğini fakat diğer iki faza geldiğini düşünelim. Bu durumda, tek fazlı trafo
grubundan oluşan üç fazlı trafo (1) çalışmaya devam ederken üç fazlı sarım ile ortak bir nüve
üstüne imal edilen üç fazlı trafo (2) serviş dışı kalır.
Her iki durumda da dört farklı bağlantı çeşidi vardır.
1.
2.
3.
4.
Y-Y
∆-∆
∆-Y
Y-∆
67
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
68
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
69
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
70
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
71
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
72
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
73
7 – Transformatörler
3 Fazlı Transformatörler
R
a
S
b
T
c
74
7 – Transformatörler
3 Fazlı Transformatörler
R
a
b
S
T
c
75
7 – Transformatörler
3 Fazlı Transformatörler
* Nötr elde etmek için Y bağlantı kullanılır. (3 faz 4 tel)
* Y-Y en nadir kullanılan bağlantı çeşididir.
* İletim hatları genellikle Y-∆ ….. ∆-Y şekilde bağlanır. İletim üçgen bağlantı ile yapılır ve
nötr hattına ihtiyaç ortadan kalkar, böylece maliyet azalmış olur.
* Zig-zag bağlantı fazların dengesiz yüklendiği durumlarda tercih edilir.
* Dağıtım trafolarının Y noktası topraklanır, böylece faz-toprak kısa devrelerinde can ve mal
kaybı önlenmiş olur. Hattın empedansı yeterli değilse, topraklama bir empedans
üzerinden yapılır. Bu empedansın hesaplanması ve topraklama yöntemleri çok önemli
konulardır ve enerji iletimi ve dağıtımı alanının konularıdır.
* Yüksek gerilim trafolarında hattın empedansı yeterli olduğu için topraklama çoğu zaman
doğrudan yapılır.
* Bunlardan başka, nötr hattının yüklenme biçimine göre de bağlantı çeşitleri bir takım farklılıklar
göstermektedir. Yine bu durum da enerji iletimi ve dağıtımının bir konusudur.
76












