iv T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

iv
T.C.
SELÇUK ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
MATRİSLERİN SİNGÜLER DEĞER
EŞİTSİZLİKLERİ
Esma BARAN
YÜKSEK LİSANS TEZİ
Matematik Anabilim Dalı
Temmuz - 2012
KONYA
Her Hakkı Saklıdır
ÖZET
YÜKSEK LİSANS TEZİ
MATRİSLERİN SİNGÜLER DEĞER EŞİTSİZLİKLERİ
Esma BARAN
Selçuk Üniversitesi Fen Bilimleri Enstitüsü
Matematik Anabilim Dalı
Danışman: Doç. Dr. Ramazan Türkmen
2012, 77 Sayfa
Jüri
Doç. Dr. Ramazan TÜRKMEN
Prof. Dr. Durmuş BOZKURT
Doç. Dr. Hakan Kasım AKMAZ
Bu tez matris teorinin temel tanım ve teoremleri ile başlamıştır ve singüler değer eşitsizlikleri ile
sonlanmıştır. Ön bilgiler bölümü hermityen ve pozitif yarı tanımlı matrisler, matris normu ve matris
ayrışımlarını içermektedir.
Ayrıca hermityen matrislerin öz değerlerinin karakterizasyonları,
majorizasyon tanımı ve blok matrislerin özellikleri ile ilgilenilmiştir.
Klasik analitik – geometri ortalama eşitsizliğinin matris versiyonları verilmiştir. Bu eşitsizlikler
arasındaki ilişki incelenmiştir. Son olarak A, B matrisleri hermityen ve A, B matrislerinden biri veya
ikisinin pozitif yarı tanımlı olduğunda A+B ve A+iB matrislerinin singüler değerleri ile ilgili bir takım
eşitsizlikler sunulmuştur.
Anahtar Kelimeler: Blok Matrisler, Hermityen matrisler, Majorizasyon, Matris
Eşitsizlikleri, Öz değerler, Pozitif Yarı tanımlı Matrisler, Singüler Değerler.
iv
ABSTRACT
MS THESIS
SINGULAR VALUE INEQUALITIES OF MATRICES
Esma BARAN
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF
SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE
IN MATHEMATICS
Advisor: Assoc. Prof. Dr. Ramazan TÜRKMEN
2012, 77 Pages
Jury
Assoc. Prof. Dr. Ramazan TÜRKMEN
Prof. Dr. Durmuş BOZKURT
Assoc. Prof. Dr. Hakan Kasım AKMAZ
The thesis starts with the fundamental theorems and definitions of matrix theory and ends with
singular values inequalities of matrices.The background chapter includes hermitian and positive
semidefinite matrices, matrix decomposition and matrix norms.. Moreover, we interested in variational
characterizations of hermitian matrices, majorization definition and properties of block matrices
We give some matrix versions of the classical arithmetic – geometric mean inequality. The
relationships between these inequalities is investigated. Finally we present several inequalities relating the
singular values of A+B and those A+iB when A and B are hermitian, and when one or both of them are
positive semidefinite.
Keywords: Block matices, Eigenvalues, Hermitian Matrices, Majorization, Matrix Inequalities, Positive
Semidefinite Matrices, Singular Values.
v
ÖNSÖZ
Bu tez çalışması, Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü Öğretim
Üyesi Doç. Dr. Ramazan TÜRKMEN danışmanlığında hazırlanarak, Selçuk
Üniversitesi Fen Bilimleri Enstitüsü’ ne yüksek lisans tezi olarak sunulmuştur.
Bu çalışmada yol gösteren ve destek olan değerli hocam Doç. Dr. Ramazan
Türkmen’e ve desteklerinden dolayı TÜBİTAK’ a teşekkürlerimi sunarım.
Bu günlere gelmemde büyük pay sahibi olan aileme ve uğradığım her hayal
kırıklığında beni hoşgörü ve sabırla dinleyen, cesaretlendiren, tekrar amacıma yönelten
canım yol arkadaşım Fadime ÖZKAN’ a teşekkürlerimi sunarım.
Esma Baran
KONYA-2012
vi
İÇİNDEKİLER
ÖZET ......................................................................................................................... iv
ABSTRACT .................................................................................................................v
ÖNSÖZ ...................................................................................................................... vi
İÇİNDEKİLER ........................................................................................................ vii
1. GİRİŞ VE KAYNAK ARAŞTIRMASI ..................................................................1
2. ÖN BİLGİLER ........................................................................................................4
2.1. Genel Kavramlar.................................................................................................4
2.2. Matris Ayrışımları .............................................................................................8
2.3. Hermityen Matrisler .......................................................................................... 10
2.4. Pozitif Tanımlı Matrisler ................................................................................... 13
2.5. Löwner Kısmi Sıralama Bağıntısı ..................................................................... 18
2.6. Matris Normu .................................................................................................. 19
3. ÖZ DEĞER VE SİNGÜLER DEĞER EŞİTSİZLİKLERİ ................................. 24
3.1 Hermityen Matrislerin Öz Değerlerinin Karakterizasyonu.................................. 24
3.2. Blok Matrislerin Singüler Değer Eşitsizlikleri ................................................... 36
3.3. Majorizasyon Eşitsizlikleri................................................................................ 41
4.ANALİTİK ORTALAMA EŞİTSİZLİKLERİN MATRİSLERE
UYGULANMASI ...................................................................................................... 45
4.1. Aritmetik Geometrik Ortalama Eşitsizliği ......................................................... 46
4.2. Heinz Ortalaması .............................................................................................. 60
5. A + iB VE A+B MATRİSLERİNİN SİNGÜLER DEĞERLERİ ........................ 66
6. SONUÇ VE ÖNERİLER....................................................................................... 74
KAYNAKLAR .......................................................................................................... 75
ÖZGEÇMİŞ............................................................................................................... 77
vii
1
1. GİRİŞ
Kompleks sayıların bir çok özelliği matrislere de genişletilmiştir. Kompleks
sayılarda reel sayıların yeri ile kompleks matrisler cümlesinde hermityen matrislerin
yeri aynıdır. Hermityen matrislere spesifik bir pozitiflik özelliği eklenerek pozitif
tanımlı
matrisler
elde
edilmiştir.
Böylece
pozitiflik
özelliği
matrislere
de
genişletilmiştir. Bir matrisin kökü, kuvveti, mutlak değeri, eşleniği ve buna benzer reel
sayılar üzerinde tanımlanan bir çok fonksiyon matrisler için de tanımlanmıştır.
Kompleks sayılar üzerinde tanımlanan bir çok eşitsizlik matrislere uygulanmaya
çalışılmıştır. Eşitsizliğin matris versiyonu doğru değilse eşitsizliğin matrislerin singüler
değer veya üniter invaryant norm versiyonları incelenmiştir.
Reel sayılar üzerinde tanımlanan ortalamalar matrisler üzerinde
de
tanımlanması bir çok problemin çözümünde önemli bir araç olmuştur. Bundan dolayı
operatörler ve matrisler üzerinde yeni ortalamalar tanımlanmaya çalışılmıştır.
Bu çalışmada temel olarak reel sayılar üzerinde tanımlanan bir eşitsizliğin
matrislere nasıl uygulandığı verilmiştir. Çalışmanın birinci bölümü Giriş ve Kaynak
Araştırması’na ayrılmış, ikinci bölümde ise hermityen ve pozitif yarı tanımlı matrisler,
matris ayrışımları, matris normları ve Löwner Kısmi Sıralama Bağıntısı hakkında bazı
temel tanım ve teoremler verilmiştir. Üçüncü bölümde majorizasyon tanımı, 2  2 blok
matrislerin bazı özellikleri, hermityen matrisin öz değerlerini ve herhangi bir matrisin
singüler değerlerini karakterize eden Courant – Fischer, Rayleigh – Ritz teoremi ve
bunların sonuçları ele alınmıştır. Dördüncü bölümde aritmetik - geometrik ortalama
eşitsizliğinin matris versiyonları ve Heinz ortalaması yer almıştır. Beşinci bölümde ise
a  b  2 a  ib eşitsizliği aracılığıyla elde edilmiş, A+B ve A+iB matrislerinin
singüler değerleri için majorizasyon eşitsizlikleri verilmiştir.
1.1. Kaynak Araştırması
Bu bölümde, matrislerin singüler değerleri ve normları hakkında yapılan
çalışmalar hakkında bilgi vereceğiz.
Bhatia ve Kittaneh (1990), herhangi A, B  M n matrisleri için
2
s j ( AB* ) 
1
s j ( AA*  BB * ) , 1  j  n
2
singüler değer eşitsizliği verilmiştir. Bu eşitsizliğin sonucu olarak A, B  M n olmak
üzere her üniter invaryant norm için
||| AB ||| 
1
||| AA*  BB * |||
2
dir.
Bhatia ve Davis (1993), Bhatia ve Kittaneh (1990) tarafından verilen norm
eşitsizliğini genelleştirmiştir. A, B, X  M n olmak üzere
||| A* XB ||| 
1
||| AA* X  XBB* |||
2
üniter invaryant norm eşitsizliği verilmiştir.
Bhatia R., Kittaneh F. (2000) Bu çalışmada, matrisler için aritmetik-geometrik
ortalama eşitsizlikleri incelenmiş ve matrislerin iz ve üniter invaryant normları için
eşitsizlikler elde edilmiştir.
Bhatia ve Kittaneh (2009), A, B matrisleri hermityen veya en az birinin pozitif
yarı tanımlı olması durumunda A + B ve A+ iB matrisleri için singüler değer eşitsizliği
sunulmuştur
Audenaert (2007), A, B  M n pozitif yarı tanımlı olmak üzere 0  v  1 için
s j ( Av B1v  A1v B v )  s j ( A  B) , 1  j  n
olduğunu göstermiştir.
Tao (2006), Bhatia ve Kittaneh tarafından 2s j ( AB* )  s j ( A* A  B*B) matrislerin
singüler değerleri için aritmetik geometrik eşitsizliği bulunmuştur. Bu çalışmada bu
eşitsizliğe denk bir eşitsizlik ve daha genel bir eşitsizlik sunulmuştur.
3
Bhatia ve Kittaneh (2008), aritmetik-geometrik ortalama eşitsizliğinin matris
versiyonları incelenmiştir.
Zhang F. (2001) Bu çalışmada ilk olarak birçok yazar tarafından elde edilen
sonuçları da içeren pozitif yarı tanımlı blok matrislerin singüler değerlerini içeren zayıf
bir logaritmik majorizasyon eşitsizliği sunulmuştur. Daha sonra pozitif yarı tanımlı blok
matrisler için daha önceki sonuçları da içeren matrislerin toplam, çarpım ve Hadamard
çarpımları için birçok matris eşitsizliği elde edilmiştir.
Zhan X. (2004) Bhatia ve Kittaneh tarafından matrislerin singüler değerleri için
2s j ( AB* )  s j ( A* A  B*B) aritmetik geometrik eşitsizliği bulunmuştur. Bu çalışmada bu
eşitsizliğin farklı bir ispatı ve bu eşitsizliğe denk bir eşitsizlik verilmiştir. Ayrıca
bulunan bu eşitsizlik kullanılarak yeni bir iz eşitsizliği ispatlanmıştır.
Zhan X. ( 2000) Bu çalışmada matrislerin pozitif yarı tanımlı matrislerin
toplamı, direkt toplamı ve farkı için için zayıf log majorizasyon, üniter invaryant norm
ve öz değer üzerine bazı eşitsizlikler sunulmuştur.
4
2. ÖN BİLGİLER
n – kare kompleks matrislerin kümesi M n ile gösterilmiştir. Benzer şekilde
n  m mertebeli kompleks matrislerin kümeside M n , m ile gösterilmiştir.
Bu bölümde matris teori ile ilgili bazı temel kavram ve teoremler verilmiştir.
2.1. Genel Kavramlar
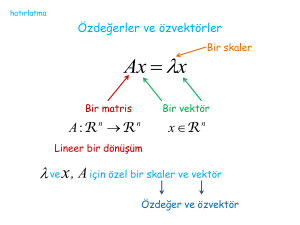
Tanım 2.1.1. V,  üzerinde vektör uzay olmak üzere
L :V  V
lineer dönüşüm olsun. Bu takdirde herhangi bir v  V için
L(v)  v
(2.1)
şartını sağlayan    varsa v vektörüne L lineer dönüşümün öz vektörü denir. Eğer
v  0 ise (2.1) şartını sağlayan sadece bir tane    vardır. Bu durumda

değerine v  V öz vektörüne ait L lineer dönüşümün öz değeri denir.
Her matris lineer dönüşümle ifade edilebileceğinden matrisin öz değer ve öz
vektörlerinden bahsedebiliriz. A  M n matrisinin temsil ettiği lineer dönüşüm L olsun.
Bu takdirde L dönüşümü
L : n  n
x  Ax
şeklindedir. Şimdi L lineer dönüşümünün öz değer ve öz vektörlerini bulalım: x   n
olmak üzere
L( x)  Ax   x  ( I  A) x  0
(2.2)
5
homojen lineer denklem sistemi elde edilir. ( I  A) matrisinin determinantından elde
edilen polinoma A matrisinin Karakteristik polinomu denir. det( I  A) = 0 deklemine
A matrisinin Karakteristik denklemi ve bu denklemin köklerine A matrisinin öz
değerleri denir. i ( 1  i  n ) için ( I  A) x  0 denklem sisteminin xi  0 çözüm
vektörüne A matrisinin öz vektörü denir.
Tanım 2.1.2. A matrisinin öz değerlerinin kümesine A matrisinin spektrumu denir ve
 ( A) ile gösterilir.
Teorem 2.1.1. (Spektral Dönüşüm Teoremi) A  M n ve f
herhangi bir polinom
olmak üzere
 ( f ( A))  f ( ( A))   f ( ) :    ( A)
(2.3)
dir. Ayrıca A tersinir bir matris ise
1

 ( A1 )  ( ( A)) 1   :    ( A) 


(2.4)
olur. (Horn ve Johnson, 1985)
Sonuç 2.1.1. A matrisinin singüler olması için gerek ve yeter şart 0  ( A) olmasıdır.
(Horn ve Johnson, 1985)
Sonuç 2.1.2. A  M n olsun. Bu takdirde k  1, 2,..., n olmak üzere
 ( Ak )  ( ( A)) k   k :    ( A)
(2.5)
dir. (2.5) eşitliğinden
1
 k ( Ak )   ( A)
elde edilir.
Teorem 2.1.2. A, B  M n olmak üzere AB ve BA matrislerinin karakteristik polinomu
aynıdır, dolayısıyla
(2.6)
6
 ( AB)   ( BA)
dir.
Fakat
A
(2.7)
ve
B
matrisleri
kare
matris
değilse
durum
farklıdır.
A  M m,n ve B  M n ,m ( m  n) olmak üzere  ( AB)  {1 , 2 ,...m } ise
m

n

 ( BA)  {1 , 2 ,...m , 0, 0,..., 0}
(2.8)
olur. Sonuç olarak AB ve BA matrislerinin karakterisitik polinomu farklıdır ve sıfır
olmayan öz değerleri aynıdır. (Murad, 2003)
Determinant ve iz fonksiyonu matrisler üzerinde tanımlıdır. Aşağıda bu
fonksiyonlarla ile ilgili temel özellikler verilmiştir.
Teorem 2.1.3. A, B  M n olsun. Bu takdirde
(i) det( AB)  det( BA)
(ii) det( AB)  det( A)det( B)
(iii) det( A)   n det( A)
n
(iv)  ( A)  {1 , 2 ,..., n } olmak üzere det A   i
i 1
eşitlikleri geçerlidir. Eğer A  M m,n ve B  M n ,m ( m  n) ise
det( BA)  0 ve det( BA)  det( AB)
dır. (Murad, 2003)
Tanım 2.1.3. A   aij   M n olmak üzere A matrisinin iz fonksiyonu
n
izA   aii
i 1
şeklinde tanımlanır.
Teorem 2.1.4. A, B  M n ve    olsun. Bu takdirde aşağıdaki eşitlikler geçerlidir.
(i) iz ( A)   iz ( A)
(ii) iz ( A  B)  iz ( A)  iz ( B)
7
(iii) iz ( AB)  iz ( BA) ( A  M m,n ve B  M n ,m matrisleri için de ifade geçerlidir.)
(iv) P tersinir bir matris olmak üzere iz ( P 1 AP)  iz ( A) dır.
n
(v)  ( A)  {1 , 2 ,..., n } olmak üzere izA   i dır. (Murad, 2003)
i 1
Tanım 2.1.4. A   aij   M n olmak üzere At   a ji  matrisine A matrisinin transpozesi
A*   a ji  matrisine de A matrisinin adjointi (eşlenik transpozesi) denir.
Teorem 2.1.5. A, B  M n ve    olsun. Bu takdirde aşağıdaki eşitlikler geçerlidir.
(i) ( A* )*  A
(ii) ( A  B)*  A*  B*
(iii) ( AB)*  B* A*
(iv) ( A)*   A*
(v) det( A* )  det( A)
(vi) iz ( A* )  iz ( A)
(vii)  ( A* )   ( A)  { :    ( A)}
(viii) A matrisi tersinir olması için gerek ve yeter şart A* matrisi de tersinir
olmasıdır, yani
( A* )1  ( A1 )* dir. (Murad, 2003)
Tanım 2.1.5. A  M m,n olmak üzere A* A matrisinin öz değerlerinin mutlak değerlerinin
kareköklerine A matrisinin singüler değeri denir ve si ( A) (i  1, 2,..., n) ile gösterilir.
Teorem 2.1.6. A  M m,n olmak üzere rank ( A)  r  min{m, n} ise A matrisi, r tane sıfır
olmayan singüler değere sahiptir. (Zhang, 1999)
Tanım 2.1.6. A M n olmak üzere
(i) A* A  I ise A matrisine üniter matris denir.
(ii) A* A  AA* ise A matrisine normal matris denir.
Matrisler Tanım 2.1.6’ da verilenlere göre sınıflandırılır. Bu sınıflandırma her
çeşit matrisin sağladığı özellikler açısından önemlidir.
Sonuç 2.1.3. Her üniter matris normal matristir.
Teorem 2.1.7. A M n olmak üzere aşağıdaki ifadeler eş değerdir.
8
(i) A üniter matristir.
(ii) A regüler bir matristir ve A1  A* dir.
(iii) A* A  I dir.
(iv) A matrisinin sütunlar kümesi ortonormaldir.
(v) A matrisinin satırlarının kümesi ortonormaldir.
(vi) x n için y  Ux olmak üzere y * y  x* x dir. (Horn ve Johnson, 1985)
Teorem 2.1.8. A   aij   M n olmak üzere aşağıdaki ifadeler eş değerdir.
(i) A normal matristir
(ii) A matrisin öz vektörleri ortonormal küme oluşturur.
2
n
(iii)
a
ij
i , j 1
n
2
  i dir. (Horn ve Johnson, 1985)
i 1
Tanım 2.1.7. A, B  M n olsun. Eğer P 1 AP  B şartını sağlayan P tersinir matrisi varsa
A ve B matrislerine benzer matrisler denir. A  B ile gösterilir. Eğer P matrisi üniter
ise A ve B matrislerine üniter benzer matrisler denir.
Teorem 2.1.9. A, B  M n benzer matrisler olsun. Bu takdirde A ve B matrislerinin
karakteristik polinomları aynıdır. O halde öz değerleri de aynıdır.
Teorem 2.1.10. A, B  M n olsun. Bu takdirde
(i) A ve AT matrisleri benzerdir
(ii) A* A ve AA* matrisleri benzerdir.
(iii) AA ve AA matrisleri benzerdir. (Zhang, 1999)
2.2. Matris Ayrışımları
Benzerlik yardımıyla matrislerin bazı özel tipteki matrislerin çarpımı şeklinde
ifade edilmesi matris teoride önemlidir. Matrislerin çarpanlarına ayrılması matris
ayrışımları ile yapılmaktadır. Bu bölümde bazı matris ayrışımları ve bu ayrışımların
öneminden bahsedilmiştir.
Tanım
2.2.1.
A M n matrisi
köşegenleştirilebilir denir.
köşegen
bir
matrise
benzerse
A
matrisine
9
Teorem 2.2.1. A M n matrisinin köşegenleştirilebilmesi için gerek ve yeter şart n tane
lineer bağımsız öz vektörü olmalıdır. (Horn ve Johnson, 1985)
Not 2.2.1. A M n matrisinin n tane farklı öz değeri varsa n tane lineer bağımsız öz
vektörü vardır. Fakat tersi doğru değildir, yani A  M n matrisinin n tane lineer bağımsız
öz vektörü olması n tane farklı öz değeri olmasını gerektirmez.
Teorem 2.2.2. A M n matrisinin
1, 2 ,..., n öz değerlerine x1 , x2 ,..., xn gibi n tane
lineer bağımsız öz vektör karşılık gelsin. Bu takdirde,
A  PP 1
olacak şekilde A’nın öz vektörlerinden oluşan terslenebilir P matrisi ve A’nın öz
değerlerinden oluşan   köş (1 , 2 ,..., n ) köşegen matrisi vardır.(Bozkurt, Türen ve
Solak, 2005)
Teorem 2.2.3. (Schur Ayrışımı) A  M n matrisinin öz değerleri 1 , 2 ,..., n olsun. Bu
durumda
*
 1


2
*


U AU 





n 
0
olacak şekilde bir U üniter matrisi vardır. (Zhang, 1999)
Teorem 2.2.4. (Spektral Ayrışım) A  M n matrisinin öz değerleri 1 , 2 ,..., n olsun.
Bu durumda A matrisinin normal olması için gerek ve yeter şart A matrisi üniter
köşegenleştirilebilir olmasıdır, yani
U * AU  köş (1 , 2 ,..., n )
10
olacak şekilde bir U üniter matrisinin vardır. (Zhang, 1999)
Not 2.2.2. A  M n matrisi normal ise n tane lineer bağımsız öz vektörü vardır.
Teorem 2.2.5. (Singüler Değer Ayrışımı) A  M m,n matrisinin rankı r ve singüler
değerleri s1 , s2 ,..., sr olsun. Bu durumda D  köş ( s1 , s2 ,..., sr ) olmak üzere
 D 0
A U 
V
 0 0
olacak şekilde bir U ve V üniter matrisi vardır. (Zhang, 1999)
Singüler değer ayrışımının önemi kare olmayan matrisler için de geçerli
olmasıdır.
Teorem 2.2.6. (Polar Ayrışımı) A  M n olmak üzere
A  PU
şartını sağlayan bir P  0 matrisi ve U üniter matrisi vardır. (Zhang, 1999)
Her A  M n matrisi Schur Ayrışımı ile üçgenleştirilebilir. A matrisinin n tane
birbirinden farklı öz değeri varsa köşegenleştirilebilir. A matrisi normal ise Spektral
Ayrışım ile üniter köşegenleştirilebilir.
2.3. Hermityen Matrisler
Tanım 2.3.1. A M n olmak üzere A*  A ise A matrisine hermityen matris denir
Eğer A*   A ise A matrisine ters hermityen matris denir.
Hermityen matris tanımından aşağıdaki sonuçlar açıktır.
(i) A =  aij   M n matrisinin hermityen olması için gerek ve yeter şart her
i, j  1,2,..., n için aij  a ji olmasıdır. Bu takdirde A hermityen matris ise köşegen
elemanları reeldir.
(ii) A  M n hermityen matris ise normal matristir.
Teorem 2.3.1. A, B  M n ve  ,   olsun. Bu takdirde
11
(i) A, B hermityen matrisler ise  A   B matrisi de hermityendir
(ii) A, B hermityen matrisler olsun. O halde AB hermityen olması için gerek ve
yeter şart AB = BA olmasıdır.
(iii) Her A  M n için A  A* , AA* ve A* A hermityendir.
(iv) A hermityen matris ise Ak matrisi de k  1,2,..., n için hermityendir.
(v) A hermityen matris ise öz değerleri reeldir.
(vi) A hermityen matris olmak üzere öz değerlerine karşılık gelen öz vektörler
diktir. Öz vektörlerinin bir ortonormal kümesi vardır. (Horn ve Johnson, 1985)
Not 2.3.1.Bir n-kare hermityen matrisin öz değerlerini
1  2  ...  n
şeklinde sıralayabiliriz.
Benzer şekilde A  M m , n matrisinin singüler değerlerini de
s1 ( A)  s2 ( A)  ...  sn ( A)  0
şeklinde sıralayabiliriz.
Teorem 2.3.2. A  M n matrisi S , T  M n hermityen olmak üzere A  S  iT şeklinde
tek türlü yazılır:
1
i
S  ( A*  A) ve T  ( A*  A)
2
2
dir. (Horn ve Johnson, 1985)
Tanım 2.3.2. A  M n olsun.
12
1
i

A  ( A*  A)  i  ( A*  A) 
2
2

1
yazılımına A matrisinin Cartesian ayrışımı denir. ( A*  A) matrisine A matrisinin reel
2
kısmı denir ve Re(A) ile gösterilir.
i *
( A  A) matrisine de A matrisinin sanal kısmı
2
denir ve Im(A) ile gösterilir.
Teorem 2.3.3. A   aij   M n matrisinin hermityen olması için gerek ve yeter şart
aşağıdaki şartlardan en az birini sağlamalıdır.
(i) x n için x* Ax dir.
(ii) A normal matris ve öz değerleri reeldir.
(iii) S  M n için S * AS hermityendir.(Horn ve Johnson, 1985)
Not 2.3.3. A   aij   M n
matrisi hermityen olsun. Bu takdirde A matrisinin öz
vektörlerinin ortonormal kümesi olduğundan ve Teorem 2.2.2’den A  U U T olacak
şekilde köşegen elemanları
A matrisinin öz değerleri olan  köşegen matrisi ve
sütunları A matrisinin öz vektörlerinden oluşan U ortogonal matrisi vardır. A matrisinin
öz değerleri 1 , 2 ,..., n ve bu öz değerlere sırasıyla karşılık gelen öz vektörler
x1 , x2 ,..., xn olmak üzere bu ayrışımı
A   x1
x2
x 
0  1
 1
  x2 
... xn  

  
0
n   

 xn 
13
şeklinde yazabiliriz.
2.4. Pozitif Tanımlı Matrisler
Bu bölümde pozitif yarı tanımlı matrislerle ilgili genel bilgi vereceğiz. Hermityen
matrislerin kümesini pozitif yarı tanımlı matrislerin kümesini kapsar.
Tanım 2.4.1. A  M n verilsin.
.,. ,  n vektör uzayı üzerinde Öklid iç çarpım
fonksiyonunu göstermek üzere her x n için
Ax, x  x* Ax  0 oluyorsa A matrisi
pozitif yarı tanımlı olarak adlandırılır ve A  0 ile gösterilir
Benzer şekilde sıfırdan farklı her x n için Ax, x  x* Ax  0 oluyorsa A
matrisine pozitif tanımlı matris denir ve A  0 ile gösterilir.
Aşağıdakiler tanımdan aşikardır.
(i)
A  M n matrisinin pozitif yarı tanımlı olması için gerek ve yeter
şart X  M n ,m matrisi için X * AX  0 olmalıdır.
(ii) Her pozitif yarı tanımlı matris hermityendir.
(iii) A  M n pozitif tanımlı ise A, A* , AT , A1 matrisleri de pozitif tanımlıdır.
Teorem 2.4.1.
(i) Pozitif yarı tanımlı (pozitif tanımlı) matrisin öz değerleri ve köşegen
elemanları negatif olmayan reel sayılardır (pozitif reel sayı).
(ii) Pozitif yarı tanımlı (pozitif tanımlı) matrisin her esas alt matrisi pozitif yarı
tanımlıdır (pozitif tanımlıdır).
(iii) Pozitif yarı tanımlı (pozitif tanımlı) matrisin determinantı ve izi negatif
değildir (pozitifdir). (Horn ve Johnson, 1985)
Sonuç 2.4.1. Pozitif yarı tanımlı (pozitif tanımlı) matrisin öz değerleri ile singüler
değerleri aynıdır.
14
Teorem 2.4.2. A, B  M n verilsin.  ,   0 olmak üzere A,B matrisleri pozitif tanımlı
(pozitif yarı tanımlı) ise  A   B matrisi de pozitif tanımlı (pozitif yarı tanımlı) dır.
(Horn ve Johnson, 1985)
İspat. A, B aynı mertebeden pozitif tanımlı matris olsun. Bu takdirde her x n için
x* Ax  0 ve x* Bx  0
olduğundan her x n için
x* ( A   B) x   x* Ax   x* Bx  0
olur.
Her pozitif yarı tanımlı matrisin hermityen matris olduğunu biliyoruz. Aşağıda
hermityen matrisin pozitif yarı tanımlı olması için gerekli kriter verilmiştir.
Teorem 2.4.3. A  M n hermityen matrisinin pozitif yarı tanımlı olması için gerek ve
yeter şart bütün öz değerlerinin negatif olmamasıdır. (Horn ve Johnson, 1985)
Benzer şekilde A  M n hermityen matrisinin pozitif tanımlı olması için gerek ve
yeter şart bütün öz değerlerinin pozitif olmasıdır.
İspat.
: A  0 ve  , A matrisinin x  0 vektörüne ait öz değeri olsun. Bu takdirde
Ax   x  x* Ax  x* x   x* x

Ax, x
x* Ax

0

x x0
x, x
15
olur.
 : A hermityen matrisinin öz değerleri negatif olmasın.( 1 , 2 ,..., n  0 ) Bu takdirde
spektral ayrışımından
A  UDU *
T
olacak şekilde U üniter ve D = köş (1 , 2 ,..., n ) matrisi vardır. y   y1 ,...., yn   U * x
olmak üzere her x n için
Ax, x  UDU * x, x  DU * x,U * x  Dy , y
sağlanır ve
Dy , y 
 1 0

 0 2
 

0 0

0  y1   y1 
   
 0  y2   y2 
,
       
   
 n  yn   yn 

 1 y1   y1 

  
 2 y2  ,  y2 
    

  
 n yn   yn 
n
  i yi 2  0
i 1
olduğundan A matrisi pozitif yarı tanımlıdır.
Sonuç 2.4.2. A  M n regüler matrisi pozitif tanımlı olması için gerek ve yeter şart A1
matrisi pozitif tanımlı olmasıdır.
Sonuç 2.4.3. A  M n olsun.
(i) A pozitif yarı tanımlı ise Ak ( k  1,2,... ) matrisi de pozitif yarı tanımlıdır.
16
(ii) A matrisi hermityen ise A2k ( k  1,2,... ) matrisi pozitif tanımlıdır.
Teorem 2.4.4. A  M n pozitif yarı tanımlı matris ve k  1,2,... olsun Bu takdirde B k  A
olacak şekilde bir tek B  0 matrisi vardır. (Horn ve Johnson, 1985)
Tanım 2.4.2. A  M n pozitif yarı tanımlı matrisi için B k  A olacak şekilde B  0
matrisine A matrisinin k. kökü denir ve B  A
1
k
ile gösterilir.
1
1
Sonuç 2.4.4. A  M n pozitif yarı tanımlı ise k  1,2,... olmak üzere ( Ak )1  ( A1 ) k dir.
Sonuç 2.4.5. A, B  M n ve A  0 olsun. A, B matrisleri değişmeli ise A1 2 , B matrisleri
de değişmelidir.
Teorem 2.4.5. A  M n matrisinin pozitif yarı tanımlı olması için gerek ve yeter şart
herhangi bir B matrisi için A  B* B olarak yazılabilmesidir. (Zhang, 1999)
İspat.
: A  M n pozitif yarı tanımlı matris olsun. Bu takdirde
1
1
1
1
A  A 2 A 2  ( A2 )* A 2
yazılabilir.
 : Herhangi bir B matrisi için A  B* B olsun. Bu takdirde her x n için iç çarpım
fonksiyonunun özelliklerinden
Ax, x  B * Bx, x  Bx, Bx  0
elde edilir. O halde A matrisi pozitif yarı tanımlıdır.
17
Sonuç 2.4.6. Her A  M n matrisi için A* A matrisi pozitif yarı tanımlıdır.
Tanım 2.4.3. Bir A matrisinin mutlak değeri
1
A   A* A  2
şeklinde tanımlanır.
Not 2.4.1. A  M m,n olsun.
Bu takdirde A  ( A* A)1 2 matrisinin öz değerlerine A
matrisinin singüler değerleri denir.
Teorem 2.4.6. A, B  M n olsun. Bu takdirde A  0 ise B* AB  0 dır. (Horn ve Johnson,
1985)
İspat. A  0 olduğundan A1 2 matrisi vardır. Bu takdirde
*
*
B* AB  B* A1 2 A1 2 B  B*  A1 2  A1 2 B   A1 2 B   A1 2 B 
olduğundan Sonuç 2.4.6 ’dan B* AB  0 dır.
Teorem 2.4.7. A, B  M n pozitif tanımlı (pozitif yarı tanımlı) olsun. AB matrisinin
pozitif tanımlı (pozitif yarı tanımlı) olması için gerek ve yeter şart A, B matrisleri
değişmeli olmalıdır. (Zhang, 1999)
İspat. A, B  M n pozitif tanımlı olmak üzere Teorem 2.1.2 den
1
1
1
1
 j ( AB)   j ( A 2 ( A 2 B))   j ( A 2 BA 2 ) , j  1,..., n
1
2
1
2
dir ve A BA  0 olduğundan  j ( AB )  0 elde edilir.
18
A,B matrisleri değişmeli ve hermityen olduğundan AB matrisi de hermityendir.
Ayrıca  j ( AB )  0 olduğundan AB matrisi pozitif yarı tanımlıdır.
2.5. Löwner Kısmi Sıralama Bağıntısı
A, B  M n hermityen matrisler olmak üzere A  B matrisi pozitif yarı tanımlı ise
A  B yazılır. Benzer şekilde A  B  0 ise A  B yazılır.
Teorem 2.5.1. Hermityen matrisler cümlesinde "  " bağıntısı bir kısmi sıralama
bağıntısıdır. Bu bağıntıya Löwner Kısmi Sıralama bağıntısı denir.
Teorem 2.5.2. A, B  M n hermityen matrisler olmak üzere A  B olması için gerek ve
yeter şart her C  M n için C* AC  C* BC sağlanmalıdır. (Zhang, 1999)
Teorem 2.5.3. A, B  M n hermityen matrisler, A pozitif tanımlı ve B pozitif yarı tanımlı
olsun. Bu takdirde A  B için gerek ve yeter şart  ( BA1 )  1 ve A  B için gerek ve
yeter şart  ( BA1 )  1 olmasıdır. (Horn ve Johnson, 1985)
Sonuç 2.5.1. A, B  M n pozitif tanımlı olsun. Bu takdirde aşağıdaki ifadeler geçerlidir.
(i) A  B olması için gerek ve yeter şart B 1  A1 olmalıdır.
(ii) A  B ise izA  izB ve det A  det B dir.
(iii) j  1,2,..., n için  j ( A)   j ( B) dir.(Horn ve Johnson, 1985)
Karekök fonksiyonunun pozitif yarı tanımlı matrisler için Löwner sıralamasını
koruduğu aşağıda teoremle verilmiştir.
Teorem 2.5.3. A, B  M n pozitif yarı tanımlı matrisler olsun. Bu takdirde A  B
1
1
ise A 2  B 2 dir. (Zhang, 1999)
1
1
1
1
İspat. A 2  B 2 matrisi hermityendir. O halde A 2  B 2 matrisinin pozitif yarı tanımlı
olduğunu göstermek için öz değerlerinin negatif olmadığını göstermeliyiz. Öz değer
tanımından
19
1
1
1
1
( A2  B 2 ) x   x  B 2 x  A2 x   x
elde edilir. Cauchy – Schwarz eşitsizliği, her x n için
x, y
2
 x, x y, y
olduğunu ifade eder. Buna göre
1
1
xA* x  ( x* Ax ) 2 ( x* Ax) 2
1
1
 ( x* Ax) 2 ( x* Bx ) 2
12
12
  ( A1 2 x )* ( A1 2 x )   ( B1 2 x)* ( B1 2 x) 
 ( A1 2 x )* ( B1 2 x )
*
1
2
1
2
x A B x
1
1
 x* A 2 ( A 2 x   x)
1
 x* Ax   x* A 2 x
1
olur. Böylece her x n için  x* A 2 x  0 olduğundan   0 dır.
2.6. Matris Normu
Tanım 2.6.1. M n kümesi  üzerinde n2 boyutlu vektör uzayıdır. ||| . |||: M n  
fonksiyonu aşağıdaki özellikleri sağlıyorsa buna Matris Normu denir. A  M n olmak
üzere
20
(1) ||| A |||  0
(2) ||| A |||  0  A  0
(3) c   için ||| cA ||| c ||| A |||
(4) || AB |||  ||| A ||| . ||| B |||
(5) ||| A  B |||  ||| A |||  ||| B |||
(1) - (4) şartlarını sağlayan fonksiyona da Genelleştirilmiş Matris Normu denir.
Sonuç 2.6.1. A  M n ve ||| . ||| matris normu olmak üzere
(i) ||| A2 |||  ||| A ||| 2
(ii) ||| I ||| 1
(iii) A regüler matris olmak üzere ||| A1 ||| 
||| I |||
||| A |||
dir. (Horn ve Johnson, 1985)
Örnek 2.6.1.
A  M n olsun.
1
2
n


(1) A 2    aij 2  ifadesine Euclidian veya  2 normu denir. Ayrıca
 i , j 1 
1
1
1
 n
2
 n
2  n
2
A 2    aij 2   iz( A* A)   i ( A* A)    si ( A) 
 i 1

 i 1

 i , j 1 
olur.
 n

(2) A 1    aij  ifadesine 1 normu denir.
 i , j 1 
(3) A matrisinin singüler değerleri s1 ( A)  s2 ( A)  ...  sn ( A) olmak üzere
21
1
 n
p
A p    si p ( A)  , 1  p  
 i 1

ifadesine Schatten p - normu denir. p =2 için Schatten p – normu Euclidian normuna
eşittir.
(4) A matrisinin singüler değerleri s1 ( A)  s2 ( A)  ...  sn ( A) olmak üzere
k
A
(k )
  si ( A)
i 1
ifadesine Ky Fan k – normu denir. p   Schatten p – normu k  1 için Ky Fan – k
normuna eşittir. p  1 için Schatten p – normu k  n için için Ky Fan – k normuna
eşittir.
Herhangi bir vektör normundan matris normu nasıl elde edileceği aşağıdaki
teoremde verilmiştir.
Teorem 2.6.1. . ,  n üzerinde vektör normu olsun. Bu takdirde, A  M n olmak üzere
||| A |||  max Ax  max
x 1
x 0
Ax
x
tanımlanan fonksiyon matris normudur. Bu norma . vektör normunun ürettiği norm
veya operatör norm denir. Operatör norm
(i) x n ve A  M n için Ax  ||| A ||| x
(ii) ||| I |||  1
özelliklerini sağlar. (Horn ve Johnson, 1985)
22
Örnek 2.6.2.
n
(1) 1 :  n  , x   xi vektör normundan
i 1
n
||| A |||1  max  aij
1 j  n
i 1
matris normu elde edilir. Bu norma sütun normu denir
(2)   : n  , x  max{ xi } vektör normundan
1 j n
n
||| A |||  max  aij
1i  n
i 1
matris normu elde edilir. Bu norma satır normu denir.
1
 n
2
(3)  2 :  n  , x    xi 2  Öklid vektör normundan
 i1 
||| A |||2  max{ i ( A* A)}
1i  n
matris normu elde edilir. Bu norma Spektral norm denir.
Tanım 2.6.2. ||| . ||| matris normu ve A  M n olmak üzere her U veV üniter matrisleri
için
||| A |||  ||| UAV |||
sağlanıyorsa . matris normuna Üniter invaryant matris normu denir.
23
Örnek 2.6.3. Euclidian normu, Schatten p- normu, Spektral norm, Ky Fan k – normu,
satır ve sütun normu üniter invaryant normdur.
24
3. ÖZ DEĞER VE SİNGÜLER DEĞER EŞİTSİZLİKLERİ
3.1 Hermityen Matrislerin Öz Değerlerinin Karakterizasyonu
Herhangi bir matrisin öz değerleri sadece karakteristik denklemin kökleri ile
karakterize edilirken hermityen matrislerin öz değerleri Courant – Fischer teoremiyle de
karakterize edilebilir. Rayleigh – Ritz teoremi bir hermityen matrisin en küçük ve en
büyük elemanlarını, Courant – Fischer teoremi ise bütün öz değerlerini karakterize eder.
Teorem 3.1.1(Rayleigh - Ritz)
A Mn
hermityen matrisinin öz değerleri
1  1  ...  n olmak üzere her x   n için
n x* x  x* Ax  1 x* x
(3.1)
1  max
x* Ax
 max
x* Ax
*
*
x
x

1
xx
(3.2)
n  min
x* Ax
 min
x* Ax
x*x 1
x* x
(3.3)
x0
x0
dir. (Horn ve Johnson, 1985)
İspat.
A Mn
hermityen
matris
olduğu
için
spektral
ayrışımdan
  köş (1 , 2 ,..., n ) olmak üzere A  U U * eşitliğini sağlayan U üniter matrisi vardır.
Bu takdirde her x   n için
n
x* Ax  (Ux* )*  (Ux* )   i (Ux* )i
2
i 1
2
elde edilir. (Ux* )i negatif olmadığından
(3.4)
25
n
n
2
n
2
n  (Ux* )i   i (Ux* )i  x* Ax  1  (Ux* )i
i 1
i 1
2
(3.5)
i 1
dır. Ayrıca U üniter matris olduğundan
n
2
n
2
 (Ux* )i  xi x* x
i 1
i 1
eşitliği sağlanır. Bu eşitlik (3.5) eşitsizliğinde uygulanırsa (3.1) eşitsizliği elde edilir.
(3.2) eşitliğini ispatlayalım. (3.3) eşitliği de benzer şekilde ispatlanır. (3.1)
eşitsizliğinden her x   n için
x* Ax
 1
x* x
(3.6)
dir. Eğer x vektörü 1 öz değerine ait öz vektör ise eşitlik sağlanır, yani
Ax1  1 x1  x1* Ax1  1 x1* x1  1 
x1* Ax1
x1* x1
(3.7)
olur. (3.6) ve (3.7) ifadelerinin sonucu olarak (3.2) eşitliği elde edilir.
Not 3.1.1. Rayleigh – Ritz teoremi ile hermityen matrislerin sadece en büyük ve en
küçük öz değerleri karakterize edilebilir. Geri kalan öz değerler hakkında yorum
yapamayız. Şimdi Rayleigh – Ritz teoremini esas alarak hermityen matrislerin diğer öz
değerlerini karakterize edelim:
26
A  M n hermityen matrisinin i öz değerine ait öz vektör ui olmak üzere
{u1 , u2 ,..., un } kümesi A matrisinin ortonormal öz vektörleri kümesi olsun. Bu takdirde
  köş (1 , 2 ,..., n ) ve U   u1 u2 ... un  olmak üzere A  U U * dır. u1 öz
vektörüne dik her x   n için
n
2
x* Ax   i U * x 
i
i 1
dir.  ui* x 
n
2
n
  i  ui* x    i  ui* x 
i 1
2
(3.8)
i
i 2
2
i
n
negatif olmadığından
n
2
2
n
x* Ax   i  ui* x    2  ui * x   2  U * x 
i2
i 2
i 2
i
2
 2 x* x  2 
x* Ax
x* x
(3.9)
elde edilir. Eğer x, u2 vektörü alınırsa öz değer tanımından (3.9) eşitsizliğinde eşitlik
sağlanır.
Au2  2u2  u2* Au2  2u2*u2  2 
u2* Au2
u2*u2
(3.10)
(3.9) ve (3.10) ifadelerinden
x* Ax
2  max *  max
x* Ax
*
x 0
x
x

1
xx
x u
x u
1
1
(3.11)
27
karakterize edilir. Bu eşitliği her öz değer için genelleştirirsek
k 
max
x 0
x u1 ,u2,...,u
k 1
n  k 
x* Ax
 max
1
x* x xu ,xu* x,...,
u
min
x0
x  un ,u n 1 ,...,u n  k 1
(3.12)
k 1
1 2
x* Ax

x* x
x* Ax , k  2,3,..., n
min
x* x 1
x u n ,un 1 ,...,un  k 1
x* Ax , k  1, 2,..., n  1
(3.13)
elde edilir.
(3.12) ve (3.13) eşitliklerinin kullanılması için öz vektörleri bilinmesi
gerektiğinden kullanımı azdır. Fakat bu eşitlikler önemli bir karakterizasyonun
gelişmesini sağlamıştır.
Teorem 3.1.2(Courant – Fischer).
A  M n hermityen matrisinin öz değerleri
1  2  ...  n olsun. Bu takdirde
w1 ,w2 ,...,wnk  n
min n
x  0, x
x  w1 ,w2 ,...,wn k
x* Ax
 k
x* x
(3.14)
min
max n
x* Ax
 k
x* x
(3.15)
max
w1 ,w2 ,..., wk 1n
x  0, x
x  w1 ,w2 ,...,wk 1
dir. (Horn ve Johnson, 1985)
İspat.
A Mn
hermityen
matris
olduğu
için
spektral
ayrışımdan
  köş (1 , 2 ,..., n ) olmak üzere A  U U * eşitliğini sağlayan U üniter matrisi vardır.
Herhangi bir {w1 , w2 ,..., wn  k }   n cümlesi
verilsin. w1 , w2 ,..., wn k vektörlerinin her
birine dik her 0  x   n için {U * x : x  n , x  0}  { y  n : y  0} olmak üzere
28
x* Ax (U * x)*  (U * x ) (U * x)*  (U * x ) y *y


 *
x* x
x* x
(U * x )* (U * x)
y y
(3.16)
dir. Ayrıca
min
x  0, xn
x  w1 , w2 ,..., wn  k
x* Ax

x* x
min
y*y
y* y
min
*
y * y
y  0, y n
y U *w1 ,U *w2 ,...,U *wn  k

y y 1
y U *w1 ,U *w2 ,...,U *wn  k
n

min
*
i
yi 2

i
yi 2

yi 2

y y 1
i 1
y U *w1 ,U *w2 ,...,U *wn  k
n

min
*
y y 1
i 1
y U *w1 ,U *w2 ,...,U *wn  k
y1  y2 .... yk 1  0
n

min
*
y y 1
ik
y U *w1 ,U *w2 ,...,U *wn  k
2
2
2
yk  yk 1 ... yn 1
i
n
 k  yi 2  k
ik
olur. O halde herhangi bir {w1 , w2 ,..., wnk }   n cümlesi
min n
x  0, x
x  w1 ,w2 ,...,wn k
x* Ax
 k
x* x
eşitsizliği vardır. (3.13) eşitliğinde k  n  k alınırsa
(3.17)
29
k 
min
x0
x un ,un 1 ,...,uk 1
x* Ax
x* x
(3.18)
elde edilir. Bu taktirde (3.17) eşitsizliğinde wi  uni1 (1  i  k  1) alınırsa eşitlik
sağlanır. Sonuç olarak
max
w1 ,w2 ,...,wnk  n
min n
x  0, x
x  w1 ,w2 ,...,wn k
x* Ax
 k
x* x
eşitliği sağlanır.
Not 3.1.2. Courant – Fischer teoremi
max
min x* Ax  k
(3.19)
boyS  k , S  n xS
x*x 1
min
boyS  n  k 1,S   n
max x* Ax  k
(3.20)
xS
x* x 1
şeklinde de ifade edilebilir.
Sonuç 3.1.1. A  M n hermityen matrisinin  j ( A) öz değerine karşılık gelen öz vektörü
e j olmak üzere ortonormal öz vektörleri {e1 , e2 ,..., en } olsun. e1 , e2 ,..., ek vektörlerinin
ürettiği uzay M olmak üzere
k ( A)  min x* Ax  min
x 1, xM
x 1, xM
x, Ax
(3.21)
30
dir. boy M  k olmak üzere, M   n herhangi alt uzay ise
k ( A)  min
x 1, xM
x, Ax
dir.
Teorem 3.1.3 (Singüler değerler için Courant – Fischer) A  M n olmak üzere
max
min Ax  sk
boyS  k , S   n xS
x* x 1
min
boyS  n  k 1, S  n
max Ax  sk
xS
x* x 1
(3.22)
(3.23)
dir. (Bhatia,1997)
Teorem 3.1.4 (Weyl) A, B  M n hermityen matris olsun. Bu takdirde k  1, 2,..., n için
k ( A)  n ( B )  k ( A  B)  k ( A)  1 ( B)
(3.24)
eşitsizliği vardır. (Horn ve Johnson, 1985)
İspat. (1) eşitsizliğinden her 0  x   n için
n ( B) 
x*Bx
 1 ( B)
x* x
(3.25)
31
dir. Bu takdirde
k ( A  B) 


max
w1 , w2 ,..., wn k  n
max
w1 , w2 ,..., wn k  n
max
w1 ,w2 ,...,wnk n
min n
x* ( A  B ) x
x* x
min n
 x* Ax x* Bx 
 *  * 
xx 
 xx
min n
 x* Ax

 *  n ( B)   k ( A)  n ( B)
 xx

x  0, x
x  w1 ,w2 ,..., wn  k
x  0, x
x  w1 ,w2 ,..., wn  k
x  0, x
x  w1 ,w2 ,...,wn k
eşitsizliği, yani (3.24) eşitsizliğinin birinci kısmı elde edilir. Eşitsizliğin ikinci kısmı da
benzer şekilde gösterilir.
Sonuç 3.1.2.(Weyl Monotonluk Teoremi) A, B  M n hermityen matris olsun. B pozitif
yarı tanımlı matris olmak üzere k  1, 2,..., n için
k ( A)  k ( A  B)
(3.26)
dir. (Horn ve Johnson, 1985)
İspat. Weyl eşitsizliğinin birinci kısmından
k ( A)  n ( B)  k ( A  B) , k  1, 2,..., n
olduğunu biliyoruz. B pozitif yarı tanımlı olduğundan k ( B)  0 dır. Bu takdirde (3.27)
eşitsizliğinden
(3.27)
32
k ( A)  k ( A  B)
elde edilir.
Sonuç 3.1.3. A, B  M n hermityen matris olsun. Bu takdirde k  1, 2,..., n için A  B ise
k ( A)  k ( B) dir.
 A B
Teorem 3.1.5(Yer Değiştirme Teoremi) H , H   *
 olacak şekilde bir n × n
B C
hermityen matris ve 1  m  n olmak üzere A, m – kare matrisi H’ın bir esas alt matrisi
olsun. Bu durumda k  1, 2,...m için
k  nm ( H )  k ( A)  k ( H )
(3.28)
dir. (Zhang, 1999)
İspat. Courant – Fischer teoreminden 1  m  n olmak üzere A m – kare matrisi için
k ( A)  max
min
x* Ax  boySmk  k 
k *
k
m
(3.29)
k ( H )  max
min
x* Hx  boySnk  k 
k *
k
n
(3.30)
Sm  
xSm , x x 1
Sn   xS n , x x 1
elde edilir. boyS0k  k olmak üzere
 x
S 0k  { y    : x  Smk }  n
0
(3.31)
33
şeklinde tanımlansın. Bu takdirde y *Hy  x* Ax olduğundan
k ( H )  max
min
x* Hx  max
min
y* Hy  max
min
x* Hx  k ( A)
k *
k *
k *
k
n
k
n
k
Sn  xSn , x x 1
S0  yS0 , y y 1
Sm
xS m , x x 1
(3.28) eşitsizliğinin ikinci kısmı elde edilir. Eşitsizliğin birinci kısmının ispatı H yerine
–H alınarak benzer şekilde gösterilir.
Sonuç 3.1.4. A  M m hermityen matris olsun. V *V  I n şartıyla herhangi bir V  M m, n
matrisi için
imn ( A)  i (V * AV )  i ( A) , 1  i  m
(3.32)
dır. (Zhang,1999)
Sonuç 3.1.5.(Ky Fan Maksimum İlkesi) A  M n hermityen matris olmak üzere
k
k
  ( A) 
i
i 1
max
*
i
 x Ax , 1  k  n
x1 , x2 ,..., xk  n ,
i 1
x1, x2 ,..., xk ortonormal
i
dır. (Zhang, 1999)
İspat. x2 ,..., xk   n herhangi ortonormal vektörler olmak üzere V   x1 x2 ... xk  olsun.
V *V  I n olduğundan (3.32) eşitsizliğinden
(3.33)
34
1 (V * AV )  1 ( A), 2 (V * AV )  2 ( A),...., k (V * AV )  k ( A)
(3.34)
eşitsizlikleri elde edilir. Bu eşitsizlikler taraf tarafa toplanırsa
k
k
 i (V * AV )   i ( A)
i 1
(3.35)
i 1
dir, ayrıca V * AV  M k olduğundan
k
k
 i (V * AV )  iz (V * AV )   xi* Axi
i 1
(3.36)
i 1
dir. O halde (3.35) ve (3.36) ifadelerinden
k
k
x
i
i 1
*
Axi   i ( A)
(3.37)
i 1
elde edilir. Eğer x1 , x2 ,..., x
k
vektörlerini
A matrisinin birim öz vektörleri olarak
seçersek
k
k
 xi* Axi   i ( A)
i 1
i 1
olur. Bu takdirde (3.37) ve (3.38) ifadelerinden
(3.38)
35
k
k
 i ( A) 
i 1
*
i
 x Ax
max
x1 , x2 ,..., xk  n ,
i 1
x1, x2 ,..., xk ortonormal
i
istenilen elde edilir.
Not 3.1.3. Ky Fan Maksimum İlkesi A  M n hermityen matris olmak üzere
k
  ( A) 
i
i 1
max iz (UAU * ) , 1  k  n
UU *  I
U M n ,k
(3.39)
şeklinde de ifade edilebilir. (Horn ve Johnson, 1985)
Sonuç 3.1.6. A  M n herhangi bir matris olsun. x1 , x2 ,..., xk   n ve y1 , y2 ,... yk   n
olmak üzere
k
k
 s ( A) 
j
j 1
max

x1 ,..., xk ortonormal
j 1
y ,..., y ortonormal
1
k
y j , Ax j , 1  k  n
(3.40)
dir. Bu eşitlik x1 , x2 ,..., xk   n olmak üzere
k
k
 s ( A) 
j
j 1
max

x1 ,..., xk ortonormal
j 1
U üniter
x j ,UAx j , 1  k  n
şeklinde de ifade edilebilir. (Bhatia, 1997)
(3.41)
36
Sonuç 3.1.7. A  M n hermityen matris olmak üzere
k
  ( A) 
i
i 1
max
det( U * AU ) , 1  k  n
*
UU  I
U M n ,k
(3.42)
dir. (Bhatia, 1997)
Sonuç 3.1.8. A  M n olmak üzere
k
 s ( A) 
i
i 1
max det( U * AU ) , 1  k  n
UU *  I
U M n ,k
(3.43)
dir. (Bhatia, 1997)
3.2. Blok Matrislerin Singüler Değer Eşitsizlikleri
Blok matisler, çeşitli matris eşitsizliklerinin elde edilmesinde önemli rol
oynamaktadır. Bu bölümde bazı özel tipteki blok matrislerin spektrumu karakterize
edilmiştir. Son olarak da blok matrislerin singüler değer eşitsizliklerine yer verilmiştir.
A 0
Lemma 3.2.1. A, B  M n olmak üzere M  
 blok matrisi tanımlansın. Bu
 0 B
takdirde
 ( M )  {1 ( A), 2 ( A),...., n ( A), 1 ( B),..., n ( B)}
dir.
(3.44)
37
A 0 
Sonuç 3.2.1. A  M n hermityen olmak üzere M  
 blok matrisi tanımlansın.
 0  A
Bu takdirde
 ( M )  {s1 ( A), s2 ( A),...., sn ( A), sn ( A),...,  s1 ( A)}
(3.45)
dir. Yani j  1, 2,..., n için
s j ( A)   j ( A   A)
(3.46)
olur. (Zhang, 1999)
0
Lemma 3.2.2. A  M m, n ve rank A  r olmak üzere M   *
A
A
blok matrisi
0 
tanımlansın.
(i) M matrisi hermityendir.
m  n r




(ii)  ( M )  { s1 ( A),  s2 ( A),....,  sr ( A), 0, 0,...., 0, sr ( A),..., s1 ( A)} dır. Dolayısıyla
j  1, 2,..., r için s j ( A)   j ( M ) dir (Zhang, 1999).
A 0
Lemma 3.2.3. A, B  M n pozitif yarı tanımlı ise M  
 blok matrisi de pozitif
 0 B
yarı tanımlıdır. (Horn ve Johnson, 1985)
 B A
Lemma 3.2.4. A, B  M n pozitif yarı tanımlı ve A  B olsun. Bu takdirde M  

 A B
blok matrisi de pozitif yarı tanımlıdır. (Zhang, 1999)
Teorem 3.2 .1 H , K  M n hermityen matris olsun. Bu takdirde
38
H
K

K
 0  H  K
H 
(3.47)
olur. (Zhang, 2001)
Teorem 3.2.2 A  M n pozitif yarı tanımlı ve B  M n ,m olsun. X  M n olmak üzere
A
 B*

B
 0  X  B* A1B
X 
(3.48)
dir. (Zhang, 2001)
Teorem 3.2.3. A, B  M n pozitif yarı tanımlı matris olmak üzere
s j ( A  B)  s j ( A  B) , 1  j  n
(3.49)
dir. (Zhan,2004)
İspat. A, B  M n pozitif yarı tanımlı matris olduğundan Lemma 3.2.3’ den A  B  0
ve B  A  0 dır. Bu takdirde
0  B
 A 0   A B

 0 B 0
B  A   0

 
dir.(3.50) ve Sonuç 3.1.3’den
0
 0  ( A  B)  ( B  A)  A  B
A 
(3.50)
39
 j (( A  B )  ( B  A))   j ( A  B )  s j ( A  B ), 1  j  2n
(3.51)
olur. Son olarak (3.46) ve (3.51) ifadelerinden
s j ( A  B ))  s j ( A  B ), 1  j  n
istenilen elde edilir.
(3.49) eşitsizliği Kittaneh (2008), çalışmasında (3.49) eşitsizliğinin genel hali
ispatlanmıştır.
Teorem 3.2.4. A, B, X  M n ve A, B pozitif yarı tanımlı matris olmak üzere
s j ( AX  XB )  X s j ( A  B ) , j  1, 2,..., n
dir. (Kittaneh, 2008)
Sonuç 3.2.2. A, B, X  M n ve A, B pozitif yarı tanımlı matris olmak üzere her üniter
invaryant norm için
||| AX  XB |||  ||| X ||| .||| A  B |||
(3.53)
dir. X  I alınırsa
||| A  B |||  ||| A  B |||
(3.54)
40
elde edilir.
M
Teorem 3.2.5 M , N  M n ve  *
K
K
 0 olsun. Bu takdirde r  min{m, n} olmak
N 
üzere
M
2s j ( K )  s j  *
K
K
, j  1, 2..., r
N 
(3.55)
dir. (Tao, 2006)
İspat.
K
M
olsun. Bu takdirde  *

0
K
 0
M , N  M n olmak üzere Q   *
K
K
0
N 
olduğundan Teorem 2.4.6’dan
 Im
0
0
0  M

 In   K *
K   Im

N  0
0   M

In    K *
K   M

N   K*
K
M
  2Q  2Q   *
N
K
K
 (3.56)
N
elde edilir. Sonuç 3.1.3 ve (3.56) ifadelerinden
M
2 j (Q)   j  *
K
K
M

s
j
*
N 
K
K
, j  1, 2..., m  n
N 
dir. Lemma 3.2.2’ den Q blok matrisinin öz değerleri
(3.57)
41
m n r




 ( M )  { s1 ( K ),  s2 ( K ),....,  sr ( K ), 0, 0,...., 0, sr ( K ),..., s1 ( K )}
olduğundan (3.57)’ den
M
2s j ( K )  s j  *
K
K
, j  1, 2..., r
N 
istenilen elde edilir.
(3.55) ve (3.49) eşitsizliklerinin, Tao (2006) çalışmasında eş değer oldukları
gösterilmiştir.
Teorem 3.2.6. Aşağıdaki ifadeler eş değerdir.
(i)
A, B  M n
pozitif
yarı
tanımlı
matris
olmak
üzere
1 j  n
için s j ( A  B )  s j ( A  B ) dır.
(ii) A, B  M n olmak üzere 1  j  n için 2s j ( XY * )  s j ( X * X  Y *Y ) dir.
(iii) M , N  M n ve
M
 K*

K
 0 olsun. Bu takdirde r  min{m, n} olmak
N 
M
üzere j  1, 2..., r için 2s j ( K )  s j  *
K
K
dir. (Tao, 2006)
N 
3.3. Majorizasyon Eşitsizlikleri
Majorizasyon kavramı eşitsizlik türetmek için son derece güçlü ve kullanışlı bir
teori olarak ortaya çıkmıştır. Issai Schur (1923)’ un öncü çalışması ‘ pozitif yarı tanımlı
bir matrisin öz değerleri, köşegen elemanlarını majorize eder’ keşfiyle matris teoriye
girmiştir. Böylece majorizasyon kavramının matris eşitsizliklerinde de önemli artmıştır.
Bu bölümde çalışmamızda yardımcı olacak bazı majorizasyon tanımları ve
eşitsizlikleri verilecektir.
42
x  ( x1 , x2 ,..., xn )   n vektörünün
bileşenlerini
büyükten
küçüğe
doğru
sıraladığımızda elde edilen vektörü x   ( x1 , x2 ,..., xn  ) şeklinde gösterelim.
x1  x2   ...  xn 
Benzer şekilde x  ( x1 , x2 ,..., xn )   n vektörünün bileşenlerini küçükten büyüğe doğru
sıraladığımızda elde edilen vektörü x   ( x1 , x2 ,..., xn  ) şeklinde gösterelim.
x1  x2   ...  xn 
Örneğin x  (2, 0,8, 2) ise x   (8, 2, 0, 2) ve x   (2, 0, 2,8) şeklindedir.
Tanım 3.3.1 x  ( x1, x2 ,..., xn ) , y  ( y1 , y2 ,..., yn )   n olmak üzere
k
k
 xi   yi , k = 1, 2, . . . ,n
i 1
i 1
ise x, y tarafından zayıf majorize edilir denir ve x  w y ile gösterilir. x  w y ’ ye ek
n
olarak
n
x
i
i 1

  yi  ise x, y tarafından majorize edilir denir ve x  y ile gösterilir.
i 1
(Zhang, 2011)
Tanım 3.3.2 x  ( x1, x2 ,..., xn ) , y  ( y1 , y2 ,..., yn )   n vektörlerinin bileşenleri negatif
olmasın. Bu takdirde
43
k
k
 xi   yi , k = 1, 2, . . . ,n
i 1
i 1
ise x, y tarafından zayıf log- majorize edilir denir ve log x  w log y ile gösterilir.
n
log x  w log y ’ ye ek olarak
n
 xi   yi ise x, y tarafından log- majorize edilir denir
i 1
i 1
ve log x  log y ile gösterilir. (Zhang, 2011)
Teorem 3.3.1 Log- majorizasyon majorizasyonu sağlar. (Zhang, 2011)
Teorem 3.3.2(Schur) H  M n hermityen matrisinin
köşegen elemanları1  i  n
olmak üzere di ( H ) ile gösterilsin. Bu takdirde d ( H )   ( H ) dir. (Zhang, 2011)
İspat. H k (1  k  n ) köşegen elemanları d1 ( H ), d 2 ( H ),...., d k ( H ) olan H matrisinin
esas alt matrisi olsun. Bu takdirde Teorem 3.1.5’ den
k
k
k
 d ( H )  iz H    ( H
i
i 1
k
i
k
i 1
)   i ( H )  d ( H )  w  ( H )
(3.58)
i 1
olur. Ayrıca k  n alınırsa
n
n
 d ( H )  iz H    ( H )
i
i 1
i
i 1
olur. Sonuç olarak (3.58) ve (3.59) ifadelerinden d ( H )   ( H ) elde edilir.
Teorem 3.3.3.(Weyl) H  M n olmak üzere  ( A)  log s ( A) dir. (Zhang, 2011)
Teorem 3.3.4. A, B  M n hermityen matris olmak üzere
(3.59)
44
(i)  ( A  B)   ( A)   ( B)
(ii)  ( A)   ( B)   ( A  B)
dir. (Zhang, 2011)
Teorem 3.3.5. A, B  M n olmak üzere
(i) s ( A  B )  w s( A)  s( B)
(ii) s ( A)  s ( B )  w s ( A  B )
dir. (Zhang, 2011)
Teorem 3.3.6. (Fan) A  M n olmak üzere Re  ( A)   (Re A) dir. (Zhang, 2011)
Teorem 3.3.7.(Fan Dominance Teoremi) A, B  M n olsun. Bu takdirde A
(k )
 B
(k )
,
1  k  n eşitsizliğinin sağlanması için gerek ve yeter şart her üniter invaryant norm için
||| A |||  ||| B ||| eşitsizliği sağlanmasıdır. (Zhang, 2011)
45
4.ANALİTİK
ORTALAMA
EŞİTSİZLİKLERİN
MATRİSLERE
UYGULANMASI
Bu bölümde literatürde
bilinen analitik ortalama eşitsizliklerinin matris
versiyonlarını inceleyeceğiz. Eşitsizlik matrislere uygulanırken aşağıdaki sıra takip
edilir.
X , Y  M n olsun.
X Y
(4.1)
s j ( X )  s j (Y ) , 1  j  n
(4.2)
k
k
 s j ( X )   s j (Y ) , 1  k  n
j 1
j 1
k
k
(4.3)
 s j ( X )   s j (Y ) ,1  k  n
j 1
(4.4)
j 1
(4.1) - (4.4) eşitsizliklerinin her biri kendisinden sonraki
eşitsizlikten kuvvetlidir.
Sonuç 3.1.3’den dolayı (4.1) eşitsizliği (4.2) eşitsizliğinden kuvvetlidir. Log –
majorizasyon majorizasyonu sağladığı için (4.3), (4.4) eşitsizliğinden kuvvetlidir. Yani
(4.1) eşitsizliği en güçlü (4.4) eşitsizliği en zayıf eşitsizliktir. Fan Dominance
teoreminden (4.4) eşitsizliği
||| X |||  ||| Y |||
üniter invaryant norm eşitsizliğine denktir.
(4.5)
46
4.1. Aritmetik Geometrik Ortalama Eşitsizliği
Tanım 4.1.1. x, y   olmak üzere
xy 
x y
2
(4.6)
eşitsizliğine aritmetik geometrik ortalama eşitsizliği denir.
(4.6 ) eşitliğinde x, y yerine sırasıyla x 2 , y 2 alınırsa ve (4.6) eşitsizliğinin her iki
tarafının karesini alırsak aritmetik geometrik eşitsizliğinin farklı iki formunu elde
ederiz:
x2  y2
2
(4.7)
( x  y )2
4
(4.8)
xy 
xy 
(4.6) - (4.8) eşitsizliklerinin her biri diğerinden elde edilebilir. Fakat bu eşitsizliklerin
her birinin matris versiyonu farklıdır. İlk olarak literatürde (4.7) eşitsizliğinin matris
formu üzerinde çalışılmıştır
(4.7) eşitsizliğinin matris versiyonları, A, B  0 olmak üzere
AB 
A2  B 2
2
s j ( AB) 
1
s j  A2  B 2 
2
(4.9)
(4.10)
47
||| AB ||| 
1
||| A2  B 2 |||
2
(4.11)
şeklinde yazılabilir. Fakat A, B  0 olmak üzere (4.9) eşitsizliği doğru değildir.
Gerçekten
1 1
1 0 
A 
ve
B


0 0  alınırsa eşitsizliğin sağlanmadığını gösterelim:
1 1


1
1
2
1
2
1
2
2 0 2  2 0
AB  (( AB) AB)  ( B A AB)  ( BA B)  

 
0 0
 0 0
*
*
*
2
3 
1
A2  B 2 
 2 


2
 1 1
3

 2 1
A2  B 2


 AB  2


2
1
 1
3
 2 1 1
A2  B 2
A2  B 2
 AB  0 
 AB
 2
  20
2
2
2
1
1
Not 4.1.1. A, B  M n pozitif yarı tanımlı matrisleri değişmeli olsun. Bu takdirde (4.9)
eşitsizliği sağlanır.
İspat. A, B  M n
pozitif yarı tanımlı matrisleri değişmeli olduğundan Teorem
2.4.7’den AB matrisi de pozitiftir. Bu takdirde
( A  B)2  0  A2  B 2  AB  BA  A2  B 2  2 AB  0  A2  B 2  2 AB  2 AB
48
Teorem 4.1.1. A, B  M n olmak üzere
1
s j ( AB* )  s j ( AA*  BB* ) , 1  j  n
2
(4.12)
dir. (Bhatia ve Kittaneh, 2008)
 A B
I 0 
İspat. X  
ve U  

 olsun. Bu takdirde
0 0
0  I 
 AA*  BB* 0 
 A* A A*B 
*
XX  
 ve X X   *
* 
0
0

B A B B
*
olur. X * X
matrisinin esas köşegen elemanlarını 0 matrisi alarak Y matrisini
oluşturalım:
 0
A* B  X * X  U ( X * X )U *
Y  *

2
B A 0 
Teorem 2.4.6’dan U ( X * X )U  0 olduğundan (4.13) eşitliğinden
(4.13)
X *X
 Y matrisi de
2
pozitif yarı tanımlıdır. Bu takdirde Sonuç 3.1.3’ den
X *X
X *X
1
Y  0 
 Y   j  X * X    j (Y ) , 1  j  2n
2
2
2
(4.14)
49
elde edilir. X * X  XX * olduğundan öz değerleri aynıdır. XX * , AA*  BB* matrisleri
pozitif yarı tanımlı olduğundan öz değerleri ile singüler değerleri aynıdır. Bu takdirde
Lemma 3.2.1’ den XX * blok matrisinin öz değerleri
 ( XX * ) =( s1 ( AA*  BB* ), s2 ( AA*  BB* ),...sn ( AA*  BB* ), 0,...,0 ) 1  j  n
(4.15)
dir. Y hermityen blok matrisinin öz değerleri Lemma 3.2.2’den s j ( A* B ) ve
 s j ( A* B ) ( 1  j  n ) dir:
 (Y )  ( s1 ( A* B ), s2 ( A* B ),...sn ( A*B ),  sn ( A* B ),...,  s1 ( A*B ))
(4.16)
Sonuç olarak (4.14), (4.15) ve (4.16) ifadelerinden
1
s j  AA*  BB*   s j ( A* B)
2
(4.17)
elde edilir ki istenendir.
(4.12) eşitsizliği (4.10) eşitsizliğinden güçlüdür. (4.12) eşitsizliğinde A, B  M n
matrisleri pozitif yarı tanımlı alınırsa (4.10) eşitsizliği elde edilir.
Sonuç 4.1.1. A, B  M n olmak üzere her üniter invaryant norm için
||| AB ||| 
1
||| AA*  BB * |||
2
(4.18)
50
dır. Özel olarak A, B  M n pozitif yarı tanımlı alınırsa
||| AB ||| 
1
||| A2  B 2 |||
2
elde edilir.
İspat. Teorem 4.1.1’ den A, B  M n için
k
 s j ( A* B) 
j 1
1 k
s j ( AA*  BB* ) , 1  k  n

2 j 1
dir. Bu takdirde
Fan Dominance teoreminden (4.19) eşitsizliği (4.18) eşitsizliğine
denktir.
Bhatia ve Davis (1993) tarafından (4.18) eşitsizliği genelleştirilmiştir. Eşitsizliğe
geçmeden önce ispatında kullanılan yardımcı teoremi verelim.
Lemma 4.1.1. AB matrisi hermityen olacak şekilde A, B herhangi matris olsun. Bu
takdirde her üniter invaryant norm için
||| AB |||  ||| Re( BA) |||
dir. (Bhatia, 1997)
Teorem 4.1.2. A, B, X  M n olsun. Bu takdirde
(4.19)
51
||| A* XB ||| 
1
||| AA* X  XBB* |||
2
(4.20)
dir. (Bhatia ve Davis ,1993)
İspat. A, B, X  M n hermityen matris ve A  B olsun. Öncelikle bu özel durum için
(4.20) eşitsizliğini ispatlayalım:
A, X matrisleri hermityen olduğundan AXA matrisi de hermityendir. Gerçekten
( AXA)*  A* X * A*  AXA
(4.21)
dir. Bu takdirde A, XA matrislerinin çarpımı AXA matrisi hermityen olduğundan
Lemma 4.1.1’ den
||| AXA ||| ||| Re( XA2 ) ||| 
1
1
||| ( XA2 )  ( XA2 )* |||  ||| XA2  A2 X |||
2
2
(4.22)
olur. Sonuç olarak A, B, X  M n hermityen matris ve A  B şartı için (4.20) eşitsizliği
ispatlanmıştır. Şimdi daha genel bir durum için (4.20) eşitsizliğini ispatlayalım:
A, B hermityen matrisler ve X herhangi bir matris olsun. T ve Y blok matrisleri
A 0
0
T 
ve Y   *

 0 B
X
X
0 
şeklinde tanımlansın. T, Y blok matrisleri hermityen olduğundan (4.22) eşitsizliğinden
52
||| TYT |||  ||| T 2Y  YT 2 |||
(4.23)
elde edilir.(4.23) eşitsizliğindeki blok matrislerin çarpımı
AXB 

 0
0
TYT   *
ve T 2Y  YT 2   2 *

* 2
0 
 BX A
B X  X A
AX 2  X 2 B 

0

olur. O halde (4.23) eşitsizliğinden istenen sonuç
||| AXB ||| 
1
||| A2 X  XB 2 |||
2
olarak elde edilir.
Son olarak A, B, X  M n matrisleri için (4.20) eşitsizliği ispatlayalım: A, B
matrislerinin polar ayrışımı U , V pozitif yarı tanımlı matrisler olmak üzere A  AU
ve
1
B  BV
olsun. Bu takdirde
1
AA* X  XBB *  A12 X  XB12
||| A* XB ||| ||| UA1 XBV
1 |||  ||| A1 XB1 |||
eşitliklerinden ve (4.24) den
(4.24)
53
1
||| AA* X  XBB* |||
2
||| A* XB ||| 
elde edilir ki, istenendir.
İki pozitif yarı tanımlı matrisin çarpımlarının pozitif olması için iki matris
değişmeli olmalıdır. Bu takdirde (4.6) eşitsizliği karekök fonksiyonu içerdiğinden
eşitsizliğin matris versiyonlarını matrislerin değişmeli olup olmadıklarına göre iki
durum altında inceleyeceğiz.
A, B  M n pozitif yarı tanımlı olsun. Bu takdirde (4.6) eşitsizliğinin matris
versiyonları
1
1
AB 2  ( A  B)
2
(4.25)
1
1
s j ( AB 2 )  s j ( A  B)
2
1
||| AB 2 |||
1
||| A  B |||
2
şeklindedir. A, B  M n pozitif yarı tanımlı matrisleri değişmeli ise
1
1
1
1
AB 2  ( AB ) 2  A 2 B 2
olduğundan (4.6) eşitsizliğinin matris versiyonları
(4.26)
(4.27)
54
1 1
1
A 2 B 2  ( A  B)
2
(4.28)
1 1
1
s( A 2 B 2 )  s j ( A  B)
2
(4.29)
1
2
1
2
||| A B ||| 
1
A B
2
(4.30)
şeklinde yazılabilir.
1
2
1
2
Not 4.1.1’ de A, B matrisleri yerine sırasıyla A , B alınırsa (4.28) eşitsizliği elde edilir.
1
1
Benzer şekilde Teorem 4.1.1 ve Sonuç 4.1.1 de A, B matrisleri yerine sırasıyla A2 , B 2
alınırsa (4.29) ve (4.30) eşitsizlikleri sağlanır.
A, B  M n pozitif yarı tanımlı olsun. Bu takdirde (4.6) eşitsizliğinin en zayıf
matris versiyonu (4.27) eşitsizliği her üniter invaryant norm için ispatlanmamıştır.
Bhatia ve Kittaneh (2000) tarafından iz normu için ispatlanmıştır. (4.26) eşitsizliği
1
1
2
s j ( AB)  s j ( A  B )
2
(4.31)
eşitsizliğine eş değerdir: (2.6) eşitliğinden X herhangi pozitif yarı tanımlı matris olmak
üzere
2
2
1
2
sj (X )  sj (X )  s j (X )  s j (X 2)
dir. Bu takdirde
(4.32)
55
1
1
1
s j ( AB 2 )  s j 2 ( AB )  s j 2 ( AB )
(4.33)
eşitsizliğinden sonuç açıktır. (4.31) eşitsizliği 2  2 matrisler için ispatlanmıştır.
Teorem 4.1.4. A, B  M n pozitif yarı tanımlı olsun. Bu takdirde
1
1
2
sn ( AB)  sn ( A  B)
2
(4.34)
1
2
1
s1 ( AB)  s1 ( A  B)
2
(4.35)
dir. (Bhatia ve Kittaneh, 2000)
İspat. (4.34) eşitsizliğini gösterelim. (4.35) eşitsizliği de benzer şekilde gösterilir.
A, B  M n matrisleri tersinir olsun. Bu takdirde
1
sn ( AB)  n 2 ( BA2 B) 
1
1
2

2
1
1 (( BA B) )
1
1
2
1

1
 1 2 (( B 1 A2 B 1 ))
2
1 (( B A B ))

1
1 ( A1 B 1 )  s1 ( A1B 1 )  1 ( B 1 A2 B 1 )  1 2 ( B 1 A2 B 1 )  11 ( A1 B 1 )
1

1

1
dir. (4.36), (4.37) ifadelerinden ve A1B1  B 2 ( B 2 A1B 2 ) B

1
(4.36)
1

1
1
1

1
1
2
(4.37)
olduğundan
1
sn ( AB )  11 ( A1B 1 )  11 ( B 2 A1B 2 )  n ( B 2 AB 2 )  sn ( A 2 B 2 )
(4.38)
56
elde edilir. (4.38) ve (4.29) ifadelerinden
1
2
1
2
1
sn ( AB)  sn ( A B )  sn ( A  B)
2
(4.39)
istenen elde edilir.
Sonuç 4.1.2. 2  2 boyutlu A, B  0 matrisleri için (4.31) eşitsizliği
1
2
1
s j ( AB)  s j ( A  B ) , j  1, 2
2
sağlanır.
Sonuç 4.1.3. 2  2 A, B  0 matrisleri için (4.26) eşitsizliği
1
1
s j ( AB 2 )  s j ( A  B) , j  1, 2
2
sağlanır.
A, B  M n pozitif yarı tanımlı matrisleri için (4.8) eşitsizliğinin en zayıf matris
versiyonu
||| AB ||| 
1
||| A2  B 2 |||
4
(4.40)
57
ve 2  2 matrisler için singüler değer formu
1
s j ( AB)  s j ( A  B) 2
4
(4.41)
ispatlanmıştır.
A, B  M n
Teorem 4.1.5.
pozitif yarı tanımlı olmak üzere (4.40) eşitsizliği
doğrudur.(Bhatia ve Kittaneh, 2000)
İspat. A, B  M n pozitif yarı tanımlı olmak üzere (4.24) eşitsizliğinden
1
2
1
2
1
2
1
2
3
2
1
2
1
2
3
2
||| AB |||  ||| A ( A B ) B |||  ||| A B  A B |||
(4.42)
elde edilir. Şimdi
3
1
1
3
s j ( A 2 B 2  A 2 B 2 )  s j ( A  B)2
(4.43)
eşitsizliğini ispatlayalım.
 12
A
X   1
 B 2

0
I 0 
 ve U  0  I  olmak üzere T matrisi


0 

A
*
T  XX   1 1
 B 2 A 2
1 1

A2 B 2 

B 
(4.44)
58
şeklinde tanımlansın. Bu takdirde


2
T   1 3
3 1
 B 2 A 2  B 2 A 2
1
3
3 1
2
2 
A2 B 2  A B 




0
1 2
2 *
(T  UT U )   1 3
3 1
2
 B 2 A 2  B 2 A 2
3
2
(4.45)
1
2
1
2
3
2

A B A B 


0
(4.46)
dir. (4.46) ve Sonuç 3.1.3’den

0
1 2 
2 *
UT U  0  T   1 3
3 1
2
 B 2 A 2  B 2 A 2
1
3
3 1
2
2 
A2 B 2  A B 


0

0
1
1

2
2
  j (T )  s j (T )   j   1 3
3 1
2
2
  B 2 A 2  B 2 A2

3
2
1
2

A B  A B 

 
0
1
2
3
2
(4.47)
elde edilir.
 A  B 0
T  X *X  
ise s (T 2 )  ( s1 ( A  B ), s2 ( A  B ),..., sn ( A  B ), 0,...,0))

0
 0
dir. Ayrıca
(4.48)
59
1
3
3 1
2
2 
1
3
1
3
1
3
1
3
3 1
3 1
3 1
3 1
A2 B 2  A B  
2
2
2
2
2
2
2
2
2 2
2 2
2 2
2 2

(
s
(
A
B

A
B
),...,
s
(
A
B

A
B
),

s
(
A
B

A
B
),...,

s
(
A
B

A
B
))
1
n
n
1



0


0

   1 3
3 1
 B 2 A 2  B 2 A2

olduğundan ve (4.47) eşitsizliğinden
3 1
1
2
2
s j ( A 2 B 2  A B )  s j ( A  B)2 , j  1, 2,..., n
2
1
3
(4.49)
istenilen elde edilir. Paralel olarak
3
2
1
2
1
2
3
2
||| A B  A B |||  ||| ( A  B) 2 |||
(4.50)
eşitsizliği de doğrudur. (4.42) ve (4.49) eşitsizliklerinden
||| AB ||| 
3 1
1 3
1
1
||| A 2 B 2  A 2 B 2 |||  ||| ( A  B ) 2 |||
2
4
eşitsizliği bulunur.
Sonuç 4.1.4. 2  2 A, B  0 matrisleri için
(4.51)
60
1
s j ( AB)  s j 2 ( A  B)
4
(4.52)
dir.
İspat. (4.31) eşitsizliğinin her iki tarafının karesi alınırsa (4.52) eşitsizliği elde edilir.
Sonuç olarak iki eşitsizlik birbirine denktir.
Sonuç 4.1.5. 2  2 A, B  0 matrisleri için (4.41) eşitsizliği sağlanır.
İspat.(4.52) eşitsizliği (4.41) eşitsizliğinden eş değer olduğunu gösterelim.X herhangi
bir pozitif yarı tanımlı matris olmak üzere
s j2( X )  s j ( X 2 )
(4.53)
dir. Bu takdirde (2.5) eşitliğinden
s j 2 ( A  B)  s j ( A  B)2
(4.54)
olduğundan sonuç açıktır.
4.2. Heinz Ortalaması
Tanım 4.2.1. a, b    olsun. 0  v  1 olmak üzere
a vb1v  a1vb
2
v
(4.55)
61
ifadesine a ile b nin Heinz Ortalaması denir. a ile b nin Heinz Ortalaması H v (a, b) ile
gösterilir ve
(1) H v (a, b)  H1v (a, b)
(2) H 1 ( a, b)  ab
2
1
(3) H 0 (a, b)  H1 (a, b)  (a  b)
2
eşitlikleri sağlanır.
Bu özelliklerden
1
ab  H v (a, b)  (a  b)
2
(4.56)
eşitsizliğinin sağlandığı açıktır. Yani iki pozitif reel sayının Heinz ortalaması, aritmetik
ortalaması ile geomerik ortalamasının ortasındadır.
(4.56) eşitsizliğinin üniter invaryant norm versiyonu
1
2
1
2
2 ||| A B |||  ||| Av B1v  A1v B v |||  ||| A  B |||
(4.57)
şeklindedir. X herhangi bir matris olmak üzere (4.57) eşitsizliğinden kuvvetli olan
1
1
2 ||| A 2 B 2 |||  ||| Av B1 v  A1 v B v |||  ||| AX  XB |||
eşitsizliği Bhatia ve Davis (1993) çalışmasında ispatlanmıştır.
(4.56) eşitsizliğinin singüler değer formu
(4.58)
62
1
1
2s j ( A 2 B 2 )  s j ( Av B1v  A1v B v )  s j ( A  B )
(4.58)
dır. eşitsizliğin birinci kısmının doğru olmadığını Audenaert (2007) çalışmasında
aşağıdaki örnekle gösterilmiştir.
2 4 2
5 0 4


Örnek 4.2.1. A   4 8 4  ve B   0 0 0  olmak üzere 0  v  0.13 için
 2 4 4 
 4 0 4 
1
2
1
2
(4.59)
s2 ( A B )  s2 ( H v ( A, B ))
dir.
Audenaert (2007) çalışmasında (4.58) eşitsizliğinin birinci kısmını ispatlamıştır.
İspatta aşağıdaki teorem kullanılmıştır.
Teorem 4.2.7. f fonksiyonu [0, ) aralığında monoton olsun. Bu takdirde A, B  0
matrisleri için
1
1
 A  B 2
 A  B 2
Af ( A)  Bf ( B )  
 ( f ( A)  f ( B )) 

 2 
 2 
(4.60)
eşitsizliği vardır. (Audenaert, 2007)
Teorem 4.1.8. A, B  M n pozitif yarı tanımlı olmak üzere 0  v  1 için
s j ( Av B1v  A1v B v )  s j ( A  B ) , 1  j  n
(4.61)
63
dir. (Audenaert, 2007)
İspat. f (t )  t r (0  t  1) fonksiyonu matris monotondur.( A  B  f ( A)  f ( B) ) Bu
takdirde (4.60) eşitsizliğinden
AAr  BB r 
1
1
1
 A  B  2 ( Ar  B r )  A  B  2
2
(4.62)
elde edilir. Paralel olarak
1
1
1
1
 j ( Ar 1  B r 1 )   j ( A  B  2 ( Ar  B r )  A  B  2 )   j ( A  B  ( Ar  B r ))
2
2
(4.63)
dır.
( A  B)( Ar  B r )  0
blok
matrisinin
sıfır
olmayan
öz
değerleri
( A  B)( Ar  B r ) matrisinin öz değerleri ile aynıdır. Ayrıca
1
 ( A  B )( Ar  B r ) 0   A 2


0
0  0


1
 2
B  A
 1
0   B 2

1
2

0   Ar  B r
 0

0 
0
0
0
eşitliğinden ( A  B)( Ar  B r )  0 blok matrisinin öz değerleri
(4.64)
64
1
 ( A  B )( Ar  B r ) 0   A 2


0
0  0


1
2
r
 r
B  A  B

0   0
 1
0   A2

0   12
B
1
  1
0   A 2 ( Ar  B r ) A 2
 1
1
0   B 2 ( Ar  B r ) A 2
1
1

A 2 ( Ar  B r ) B 2 
0
1
1 
r
r
2
2
B ( A  B )B 
matrisinin öz değerleri ile aynıdır. Bu takdirde Teorem 2.3.5’ den
1
 12 r
r
2
A
(
A

B
)
A

r
r
2s j ( A ( A  B ) B )  s j  1
1
 B 2 ( Ar  B r ) A 2

1
2
1
2
1
1

A 2 ( Ar  B r ) B 2 
  j (( A  B )( Ar  B r ))
1
1 
B 2 ( Ar  B r ) B 2 
(4.65)
elde edilir. (4.63) ve (4.65) eşitsizliklerinden
1
1
2s j ( A 2 ( Ar  B r ) B 2 )   j ( Ar 1  B r 1 )
(4.66)
1
1
eşitsizliği sağlanır. Bu eşitsizlikte A, B matrisleri yerine sırasıyla A1r B1r matrisleri
alınırsa
2s j ( A
2 r 1
2 r2
B
1
2 r 1
olur. 1  v 
A
1
2 r 2
B
2 r 1
2 r 2
)   j ( A  B)  s j ( A  B) , 0  r  1
(4.67)
1
şeklinde tanımlanırsa (4.67) eşitsizliği
2r  2
2s j ( A  B )  s j ( Av B1v  A1v B v ) ,
1
3
1
 v  ve 0  v 
2
4
4
(4.68)
65
eşitsizliğine eş değerdir.
Sonuç olarak
(4.61) eşitsizliğini
1
3
1
 v   0  v   için gösterildi. Şimdi
2
4
4
3
1
1
 v  1   v   aralığı için gösterelim:
4
2
4
( A  B)( Ar  B r )  0
blok
matrisinin
sıfır
olmayan
öz
değerleri
( A  B)( Ar  B r ) matrisinin öz değerleri ile aynıdır. Ayrıca
r
 ( A  B )( A  B ) 0   A 2


0
0  0


r
r
r
 2
B  A
 r
0   B 2

r
2

0  A  B 0 
0
 0
0


0
(4.69)
eşitliğinden ( A  B)( Ar  B r )  0 blok matrisinin öz değerleri
r
 ( A  B )( Ar  B r ) 0   A 2



0
0  0


r
  A  B 0   A2

B 


0   2r
0   0
B
r
2
blok matrisinin öz değerleri ile aynıdır.
edilirken
uygulanan
işlemler
sırasıyla
r
  r
0   A2 ( A  B) A 2
 r
r
0   B 2 ( A  B ) A 2
r
r

A 2 ( A  B) B 2 
0
r
r 
2
2 
B ( A  B) B 
İspatın devamında (4.68) eşitsizliği elde
uygulanarak
3
1
1
 v  1   v   değerleri için doğru olduğu görülür.
4
2
4
(4.61)
eşitsizliğinin
66
5. A + iB VE A+B MATRİSLERİNİN SİNGÜLER DEĞERLERİ
Bu bölümde a, b   olmak üzere
(5.1)
a  b  2 a  ib
eşitsizliğinin matris versiyonları verilmiştir.
A, B  M n pozitif tanımlı olmak üzere
(5.2)
A  B  2 A  iB
eşitsizliğinin doğru olmadığı aşağıdaki örnekte gösterilmiştir.
 2 1
1 0
Örnek 5.1. A  
ve B  

 olsun. Bu takdirde
 1 1
0 0
2 A  iB 
olup
6  2 3i 


(4  2)1 2  3  i 2  2 
1
2 A  iB  ( A  B ) negatiftir. (Bhatia ve Kittaneh, 2009)
(5.1) eşitsizliğinin en güçlü matris versiyonu, (5.2) eşitsizliğinin doğru olmadığı
gösterilmiştir. Fakat (5.2) eşitsizliğinden zayıf, (5.1)
versiyonun doğruluğu kanıtlanmıştır.
Teorem 5.1. A, B  M n pozitif yarı tanımlı olmak üzere
eşitsizliğinin singüler değer
67
(5.3)
s j ( A  B )  2 s j ( A  iB )
dir . (Bhatia ve Kittaneh, 2009)
İspat.
A, B  M n pozitif yarı tanımlı olsun. A  B pozitif yarı tanımlı matrisinin
 j ( A  B ) öz değerine karşılık gelen öz vektörü e j olmak üzere ortonormal öz
vektörleri {e1 , e2 ,..., en } olsun. M, e1 , e2 ,..., e j vektörlerinin ürettiği uzay olmak üzere
Sonuç 3.1.1’den
s j ( A  B )  min
(5.5)
x, ( A  B ) x
x 1, xM
olur. Bu takdirde (5.5) ve (5.1) ifadelerinden
s j ( A  B)  min
x, ( A  B ) x
x 1, xM
 min
x 1, xM

x, Ax  x, Bx

 2 min
x, Ax  i x, Bx
 2 min
x, ( A  iB) x
x 1, xM
x 1, xM
dir. Sonuç olarak
s j ( A  B )  min
x 1, xM
x, ( A  iB ) x
(5.7)
68
eşitsizliği elde edilir. Cauchy – Schwarz eşitsizliği, her x   n için
x, y  x y
(5.8)
olduğunu ifade eder. (5.7) eşitsizliğine Cauchy – Schwarz eşitsizliği uygulanırsa
s j ( A  B )  2 min
x 1, xM
x, ( A  iB ) x
 2 min ( A  iB ) x x
x 1, xM
(5.8)
 2 min ( A  iB ) x
x 1, xM
olur. Teorem 3.1.3 ( Singüler değerler için Courant – Fischer) ve (5.8) ifadesinden
s j ( A  B)  2 min ( A  iB) x  2
x 1, xM
max
min Ax  2s j ( A  iB)
boyS  j , S   n xS
x* x 1
(5.9)
istenilen sonuç elde edilir.
Sonuç 5.1. A, B  M n pozitif yarı tanımlı olmak üzere
k
k
 s j ( A  B)   s j ( A  iB) , k  1, 2,..., n
j 1
yani
j 1
(5.10)
69
s( A  B)  w log s( A  iB)
(5.11)
dir.
(5.11) eşitsizliği Sonuç 5.1’ de pozitif yarı tanımlı matrisler için gösterilmiştir.
(5.11) eşitsizliği A  M n pozitif yarı tanımlı, B  M n hermityen matris olmak üzere
Bhatia ve Kittaneh (2009) tarafından ispatlanmıştır.
Teorem 5.2. A  M n pozitif yarı tanımlı, B  M n hermityen matris olmak üzere
k
k
 s ( A  B)   s ( A  iB) , k  1, 2,..., n
j
j 1
j
j 1
dir . (Bhatia ve Kittaneh, 2009)
İspat. A  M n pozitif yarı tanımlı, B  M n hermityen matris olsun. Teorem 2.1.3
(i),(ii) ve (iv) ifadelerinden ve (5.1) eşitsizliğinden
det( A  B)  det A1 2 ( I  A1 2 BA1 2 ) A1 2
 det A1 2 det( I  A1 2 BA1 2 ) det A1 2
 det A det( I  A1 2 BA1 2 )
n
 det A  1   j ( A1 2 BA1 2 )
j 1
n
 det A  2 1  i j ( A1 2 BA1 2 )
j 1
 2n det A det( I  iA1 2 BA1 2 )
 2n det( A  iB)
(5.12)
70
olur. Sonuç olarak A  M n pozitif yarı tanımlı, B  M n için
det( A  B )  2 n det( A  iB )
(5.13)
eşitsizliği elde edilir.
Sonuç 3.1.8’den
k
 s ( A  B) 
j
j 1
max det( U * ( A  B )U ), 1  k  n
(5.14)
UU *  I
U M n ,k
dir. O halde
k
 s ( A  B)  det(U
*
j
( A  B)U ) , 1  k  n
(5.15)
j 1
eşitliğini sağlayan en az bir U *U  I olmak üzere U  M n ,k matrisi vardır.
A 0
olduğundan
U * AU  0 dır. Bu takdirde (5.15)
eşitsizliği uygulanabilir:
k
 s ( A  B)  det(U
j
*
( A  B)U )
j 1
 det (U * AU  U * BU )
 2 n det(U * AU  iU * BU )
eşitliğine (5.13)
71
 2 n det U * ( A  iB)U
(5.16)
Sonuç 3.1.8’ den
k
 s ( A  iB)  max det(V
j
j 1
VV *  I
V M n ,k
*
( A  iB )V ) , 1  k  n
(5.17)
dir. Bu takdirde (5.16) ve (5.17) ifadelerinden 1  k  n için
k
k
det( V * ( A  iB )V )   s j ( A  iB )
 s j ( A  B)  2n det U * ( A  iB)U  max
*
VV  I
V M n ,k
j 1
(5.18)
j 1
istenilen elde edilir.
Sonuç 5.2. Log – majorizasyon majorizasyonu sağladığı için Teorem 5.2’ den A  M n
pozitif yarı tanımlı, B  M n hermityen matris olmak üzere
k
k
 s j ( A  B)  s j ( A  iB ) , k  1, 2,..., n
j 1
j 1
(5.19)
yani,
s( A  B)  w s ( A  iB)
(5.20)
72
dir.
(5.19) eşitsizliğinin doğru olması için A matrisinin pozitif yarı tanımlı olması
gerekmez. Çünkü A, B  M n hermityen matrisleri için de ispatlanmıştır.
Teorem 5.3. A, B  M n hermityen matris olmak üzere
k
k
 s j ( A  B)  s j ( A  iB ) , k  1, 2,..., n
j 1
(5.21)
j 1
dır. (Bhatia ve Kittaneh, 2009)
İspat. A, B  M n hermityen matris olmak üzere A  B hermityen matrisinin  j ( A  B )
öz değerine karşılık gelen öz vektörü e j olmak üzere ortonormal öz vektörleri
{e1 , e2 ,..., en } olsun. (5.1) eşitsizliğinden
s j ( A  B )  e j , ( A  B )e j
 e j , Ae j  e j , Be j
 2 e j , Ae j  i e j , Be j
 2 e j , ( A  iBe j
(5.22)
elde edilir.(5.22) eşitsizliğinden
k
k
 s j ( A  B)  2  e j , ( A  iBe j
j 1
j 1
(5.23)
73
dir. Sonuç 3.1.6 ‘ dan x1 , x2 ,..., xk   n ve y1 , y2 ,... yk   n olmak üzere
k
k
 s ( A  iB) 
i
i 1
max

y1 , y2 ,..., yk ortonormal
i 1
x1 , x2 ,..., xk ortonormal
yi , ( A  iB ) xi
(5.24)
dir.(5.24) ve (5.25) ifadelerinden
k
k
 s j ( A  B)  2  e j , ( A  iBe j 
j 1
j 1
max
k
k

y j , Ax j   s j ( A  iB )
x1 ,..., xk ortonormal
j 1
y ,..., y ortonormal
1
k
j 1
istenilen elde edilir.
Sonuç 5.3. A, B  M n hermityen matris ve ||| . ||| üniter invaryant norm olmak üzere
||| A  B |||  ||| A  iB |||
dir.
(5.25)
74
6. SONUÇ VE ÖNERİLER
Bu çalışmada literatürde, reel sayılarda tanmlanan bazı eşitsiliklerin ve
ortalamaların matrislere nasıl uygulandığı incelenmiştir. Matrisler üzerinde yeni
ortalamalar tanımlanarak farklı eşitsizlikler elde edilebilir.
75
KAYNAKLAR
Audenaert K., 2007, A singular value inequality for Heinz means, Linear Algebra
Appl. 422 , 279-283.
Bhatia R., , 2007, Positive Definite Matrices, Princeton University Press, Princeton.
Bhatia, R.,1997, Matrix Analysis, Springer–Verlang, New York.
Bhatia, R., Kittaneh, F., 2000,Notes on matrix arithmetic-geometric mean inequalities,
Linear Algebra and its Applications, 308,203-211
Bhatia, R., Davis, C., 1993, More Matrix forms of the arithmetic-geometric mean
inequality, SIAM J. Matrix Analysis, 14, 132-136.
Bhatia, R., Kittaneh, F., 1990, On the singular values of a product of operators, SIAM J.
Matrix Analysis, 11,272-277.
Bhatia R., Kittaneh F., 2008, The Matrix Arithmetic-Geometric Mean Inequality
revisited, Linear Algebra and its Applications, 428, 2177-2191.
Bhatia R. ve Kittaneh F., 2009, The singular values of A + B and A + iB, Linear
Algebra and its Applications, 431, 1502–1508.
Bozkurt D., Türen B., ve Solak S., 2005, Lineer Cebir, Selçuk Üniversitesi Yayınları.
Horn, R. A., Johnson, C. R., 1991,Topics in Matrix Analysis, Cambridge University
Pres.
Horn, R. A., Johnson, C. R., 1985, Matrix Analysis, Cambridge University Pres.
Lang, S., 1986, Introduction to Linear Algebra, Springer-Verlang, New York.
Marshall, A.W., Olkin, I., 1979, Inequalities: Theory of Majorization and its
Applications, Academic Pres.
Murad, M.A., 2003, The Löwner Ordering of Hermitian Matrices, Yüksek Lisans Tezi,
The University of Jordan, Faculty of GraduadeStudies.
Tao, Y., 2006, More results on singular value inequalities of matrices, Linear Algebra
and its Applications,416, 724-729
76
Ulukök Z.,2009, 2  2 Blok Matrisler için Eşitsizlikler, Yüksek Lisans Tezi, Selçuk
Üniversitesi Fen Bilimleri Enstitüsü, Konya.
Zhan, X.,2004, On some matrix inequalities, Linear Algebra Appl.,376,299-303.
Zhan X. , 2000, Singular values of differences of positive semidefinite matrices, SIAM
J. Matrix Anal. Appl., 22, (3), 819-823.
Zhang, F., 1999, Matrix Theory:Basic and Techniques, Springer–Verlang, NewYork.
Zhang, F., 2011, Matrix Theory:Basic and Techniques, Springer–Verlang, NewYork.
Zhang, F., 2001, Matrix Inequalities by Means of Block Matrices, Math. Ineq. Apply.,
4(4), 481-490.
77
ÖZGEÇMİŞ
KİŞİSEL BİLGİLER
Adı Soyadı
Uyruğu
Doğum Yeri ve Tarihi
Telefon
Faks
e-mail
:
:
:
:
:
:
Esma Baran
Türk
Meram\ KONYA, 04.12.1988
0 (506)334 03 91
husna_baran42@hotmail.com
EĞİTİM
Derece
Lise
:
Üniversite
:
Yüksek Lisans :
Doktora
:
Adı, İlçe, İl
Dolapoğlu Anadolu Lisesi, Selçuklu, KONYA
Selçuk Üniversitesi, Selçuklu, KONYA
Selçuk Üniversitesi, Selçuklu, KONYA
Bitirme Yılı
2006
2010
İŞ DENEYİMLERİ
Yıl
Görevi
2010
Kurum
Çankırı Karatekin Üniversitesi Fen
Fakültesi
2011
Selçuk Üniversitesi Fen Fakültesi
Araş. Gör
Araş. Gör