2.2
ro =
1
=
gm
µ . COX
1
1
=
W
(V − VT ) β (VGS − VT )
L GS
(2.2)
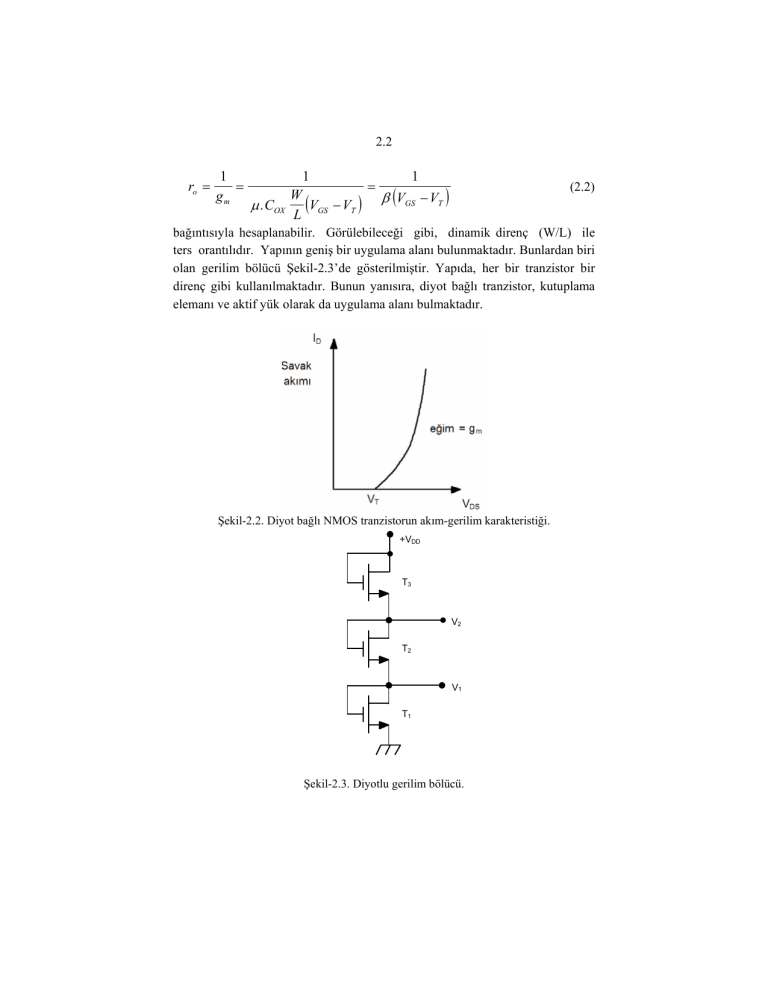
bağıntısıyla hesaplanabilir. Görülebileceği gibi, dinamik direnç (W/L) ile
ters orantılıdır. Yapının geniş bir uygulama alanı bulunmaktadır. Bunlardan biri
olan gerilim bölücü Şekil-2.3’de gösterilmiştir. Yapıda, her bir tranzistor bir
direnç gibi kullanılmaktadır. Bunun yanısıra, diyot bağlı tranzistor, kutuplama
elemanı ve aktif yük olarak da uygulama alanı bulmaktadır.
Şekil-2.2. Diyot bağlı NMOS tranzistorun akım-gerilim karakteristiği.
+VDD
T3
V2
T2
V1
T1
Şekil-2.3. Diyotlu gerilim bölücü.
2.9
şeklinde ortalama ve fark büyüklükler tanımlansın. Bunların akım-gerilim
bağıntılarında yerlerine konması halinde, yüksek dereceden terimler ihmal
edilirse, dengesizlikler nedeniyle akımın nominal değerinde ortaya çıkacak bağıl
hata
W
∆I D ∆ L
∆VT
=
−2
W
ID
VGS − VT
L
(2.15)
olur. Bağıntıdan görülebileceği gibi, akım dengesizliğinin iki bileşeni
bulunmaktadır. Bunlardan birincisi geometriye bağlıdır ve kutuplamadan
bağımsızdır. İkinci bileşen ise eşik dengesizliğinden kaynaklanmaktadır ve
kutuplamaya bağlıdır, diğer bir deyişle VGS-VT azaldıkça artmaktadır.
2.3. Kuvvetlendirici Yapıları
Bu bölümde, NMOS ve CMOS aktif yüklü kuvvetlendirici yapıları ele
alınacaktır. İlk başta, sadece kanal oluşturmalı NMOS yapılar incelenecek,
daha sonra kanal oluşturmalı ve kanal ayarlamalı tranzistorların birlikte
kullanıldıkları yapılara yer verilecek, en sonda ise CMOS yapılara
değinilecektir.
Aktif yüklü savak çıkışlı kuvvetlendirici yapısı
g mb2.vbs2
ro2
g m2.vgs2
1
s2, d1
+VO
g1
+
Vi
g m1.vgs1
ro1
-
s1, g2 , b
Şekil-2.11. Savak çıkışlı kuvvetlendirici ve bu yapının eşdeğer devresi.
Aktif yüklü savak çıkışlı bir kuvvetlendirici devresi Şekil-2.11’de
gösterilmiştir. Yine, yapının eşdeğer devresi şekil üzerinde yer almaktadır.
Devrenin gerilim kazancı eşdeğer devre yardımıyla hesaplanabilir. Devre
2.13
Diyot yüklü NMOS kuvvetlendiricinin frekans cevabı
(a)
Şekil-2.14. Diyot yüklü kuvvetlendiricinin küçük işaret eşdeğer devresi.
Diyot yüklü NMOS kuvvetlendiricinin frekans cevabı eşdeğer devre
yardımıyla incelenebilir. Eşdeğer devre Şekil-2.14’de görülmektedir. Eşdeğer
devredeki büyüklükler
G Leq = (1 / ro1 ) + (1 / ro 2 ) + g m2 + g mb 2
(2.25)
2.15
tek bir yük elemanına göre yarı geçit alanına gereksinme göstermekte, böylece
etkin yük kapasitesi CLeq azalmaktadır. Buna karşılık, iki diyot seri bağlanarak
yük oluşturulduğundan, alçak frekanslardaki kazanç önceki devreyle aynı olur.
+VDD
T3
T2
+VO
T1
+VI
Şekil-2.15. Parçalı yüklü kuvvetlendirici.
Kaskod devre
+VDD
T3
+VO
+VB
T2
Vd1
+VI
T1
Şekil-2.16a. Kaskod yüklü kuvvetlendirici.
Aktif yüklü kuvvetlendiricilerde yük tranzistorları kendilerini süren kata
önemli bir kapasitif yük oluşturabilirler. Cgs ve Cgd kapasiteleri sorun yaratmaya
başlarlar, özellikle Cgd kapasitesi Miller etkisi nedeniyle sorun çıkarır. Bu
problem kaskod devre yardımıyla çözülebilir. Kaskod devre Şekil-2.16a’da
verilmiştir. Kaskod yapıda, T1 tranzistorunun savak ucuna ortak geçitli olarak
2.16
çalışan T2 tranzistoru bağlanmıştır. Devrenin gerilim kazancı eşdeğer devre
yardımıyla hesaplanabilir. Girişten ilk tranzistorun savak ucuna kadar olan
kazanç
vd 1
g
(W / L)1
= − m1 α b 2 = −
α
vi
gm 2
(W / L) 2 b 2
(2.33)
ikinci tranzistorun kaynak ucundan savak ucuna kadar olan kazanç da
vo
g
1
= α b 3 m2
vd 1
g m3 α b 2
bağıntısıyla verilir. Buradan hareketle toplam kazanç hesaplanırsa
vo
g
(W / L)1
1
= −α b 3 m1
=−
vi
g m3 α b 2
(W / L) 3
(2.34)
bulunur. Miller etkisi nedeniyle Cgd1 kapasitesi vd1 /vi ile çarpılarak girişe
yansır. Bu etkiyi minimum düzeyde tutabilmek üzere, (W/L)1 = (W/L)2
seçilerek vd1 /vi = 1 olması sağlanır. (W/L)3 oranı küçük tutularak da
istenilen kazanç değeri sağlanır.
Kaskod devrenin frekans cevabı
RS
V1
+
VI
V2
VO
gm2.v2
g m1.v1
Cgs1
g2
-1
C2
gm3
-1
CLeq
Şekil-2.16b Kaskod devrenin küçük işaret eşdeğer devresi.
Kaskod devrenin frekans cevabı eşdeğer devre kullanılarak incelenebilir.
Kaskod devrenin eşdeğer devresi Şekil-2.16b’de görülmektedir. Eşdeğer devrede
görülen büyüklükler
2.17
g 2 = g m2 +
1
ro1
C1 = C gs1 + (1 + g m1 / g m2 ). C gd 1
C2 = C gd 1 + Cdb1 + C gs 2 + Csb 2
C Leq = C gd 2 + Cdb 2 + Csb 3 + C gs 3 + C L
(2.35)
şeklindedir. Miller teoreminin uygulanmasıyla devrenin transfer fonksiyonu
KV ( s) =
GS g m2 ( sC gd 1 − g m1 )
( sC1 + GS ).( sC2 + g 2 ).( sC Leq + g m3 )
(2.36)
olur. Bu transfer fonksiyonunun sıfır ve kutupları
g m1
C gd 1
(2.37)
s p1 = −
GS
C1
(2.38)
s p2 = −
g2
C2
(2.39)
sp3 = −
gm 3
CLeq
(2.40)
sz =
şeklindedir. Pratikte karşılaşılan değerler ele alınırsa, |sp1 | << sz , |sp2| ,|sp3| ve
böylece sp1 baskın kutup olur. Buna göre, kazanç fonksiyonunun 3 dB düşme
frekansı
f 3dB =
GS
2π . C1
(2.41)
olur. Tipik olarak gm1 = gm2 olduğundan, kaskod devrede Cin giriş kapasitesi
(2.42)
Cin = C1 = C gs1 + 2C gd 1
değerindedir. Böylece, 3 dB frekansı da
f 3dB =
GS
2π .(C gs1 + 2. C gd 1 )
(2.43)
olur . (2.28) ve (2.30) bağıntılarıyla karşılaştırılırsa, giriş kapasitesinin
küçülmesi nedeniyle band genişliğinin artacağı kolayca görülebilir.